Modelska analiza I
12. naloga: Metoda maksimalne entropije in linearna napoved
Uvod
V nalogi se bomo ukvarjali z linearnimi sistemi in linearno napovedjo prihodnjega obnašanja za tak sistema, če poznamo dosedanji signal. Sistem lahko razumemo kot filter – za neko časovno zaporedje vhodov \(u_n, n = 1, 2, \dots\), je signal na izhodu takega linearnega sistema linearna kombinacije \begin{equation}s_n = -\sum_{k = 1}^p a_k s_{n - k} + G \sum_{k = 0}^q b_k u_{n - k}, \label{eq:FIR}\end{equation} pri čemer je \(p\) t. i. red filtra in je \(p < \infty\) za filter s končnim odzivom (ang. finite impulse response ali FIR). Za \(k = 1, 2, \dots, p\) sta \(\{a_k\}_k\) in \(\{b_k\}_k\) končna nabora koeficientov filtra. Skalar \(g\) je ojačitveni faktor za vhod. V tej nalogi se bomo posvetili zgolj prvemu členu, izpeljave pa lahko ostanejo splošne. Z uporabo Z-transformacije \(S(z) = \sum_{n = -\infty}^\infty s_n z^{-n}\) lahko celotno enačbo 1 preslikamo v kompleksno frekvenčno domeno \[S(z) = -\sum_{n = -\infty}^\infty \sum_{k = 1}^p a_k s_{n - k} z^{-n} + \sum_{n = -\infty}^\infty \sum_{k = 0}^q b_k u_{n - k} z^{-n}.\] Z preureditvijo indeksov lahko to zapišemo kot \[S(z) = - S(z) \cdot \sum_{k = 1}^p a_k z^{-k} + G b_0 \cdot U(z) + U(z) \cdot G \sum_{k = 1}^q b_k z^{-k},\] kar pomeni, da linearni sistem 1 opisuje prenosna funkcija \[H(z) = \frac{S(z)}{U(z)} = G\frac{1 + \sum_{k = 1}^{q} b_k z^{-k}}{1 + \sum_{k = 1}^{p} a_k z^{-k}}.\] To obliko prenosne funkcije bomo v nadaljevanju uporabili za oceno spektrov.
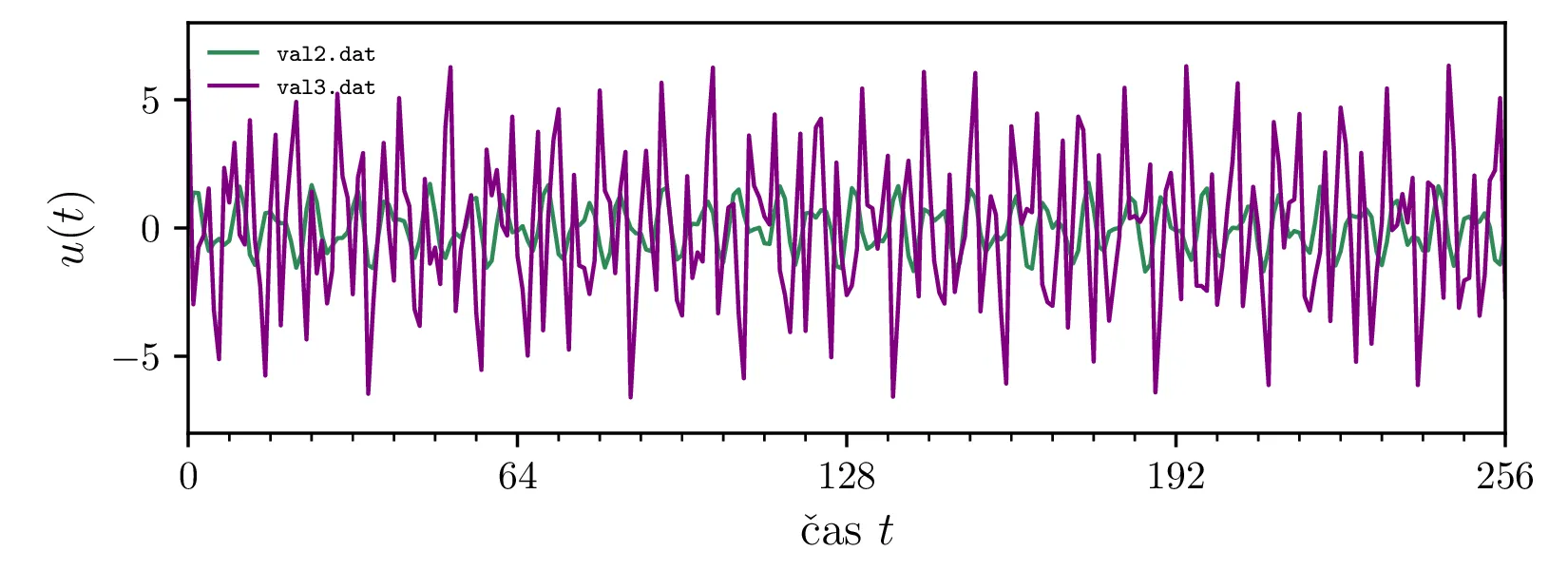
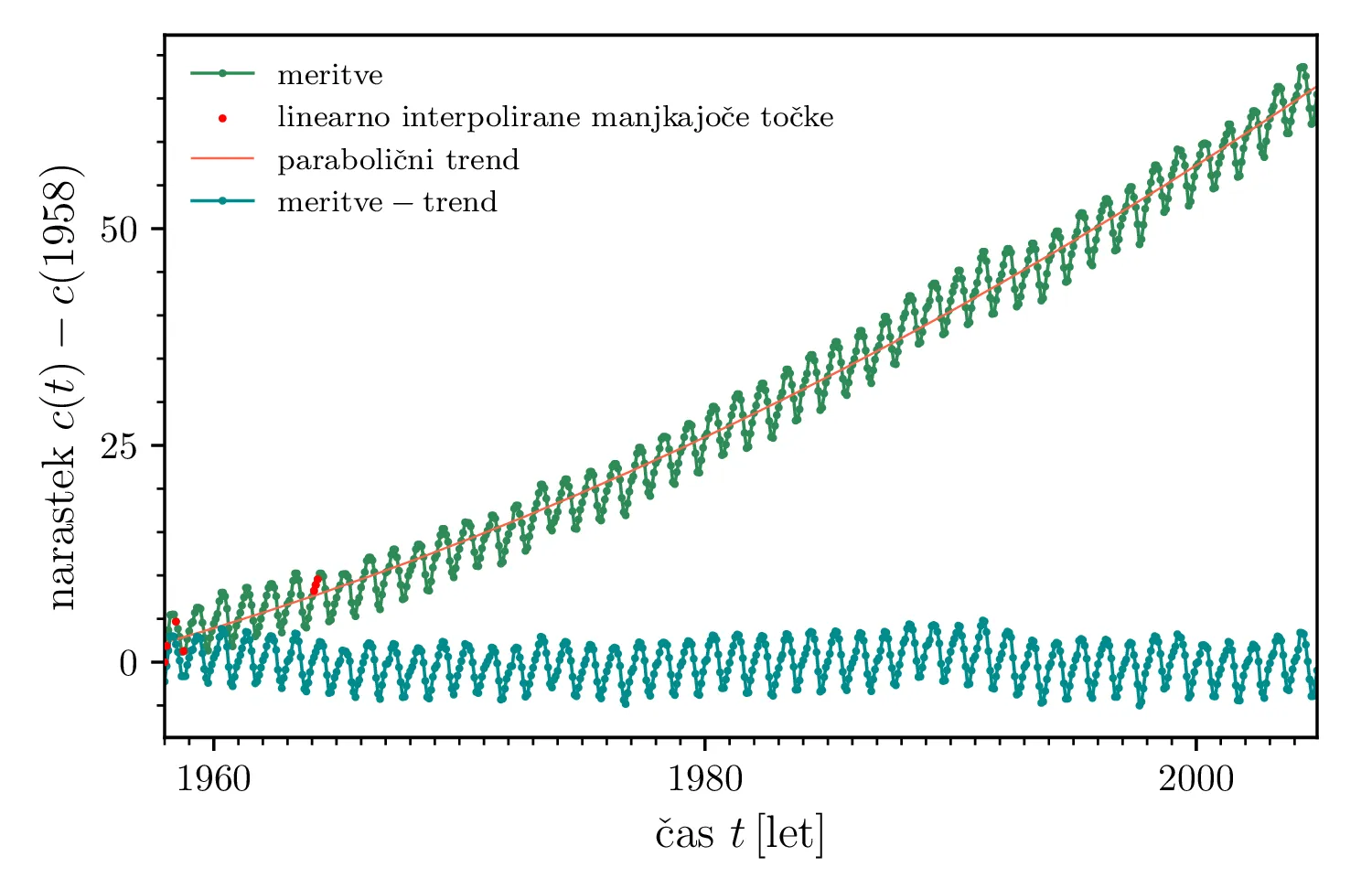
val2 in val3. (Desno) Signal
koncentracije \(\mathrm{CO}_2\). Manjkajoče točke (rdeča barva) so linearno
interpolirane, prvo meritev pa si izmislimo kot \(312\,\mathrm{ppm}\).
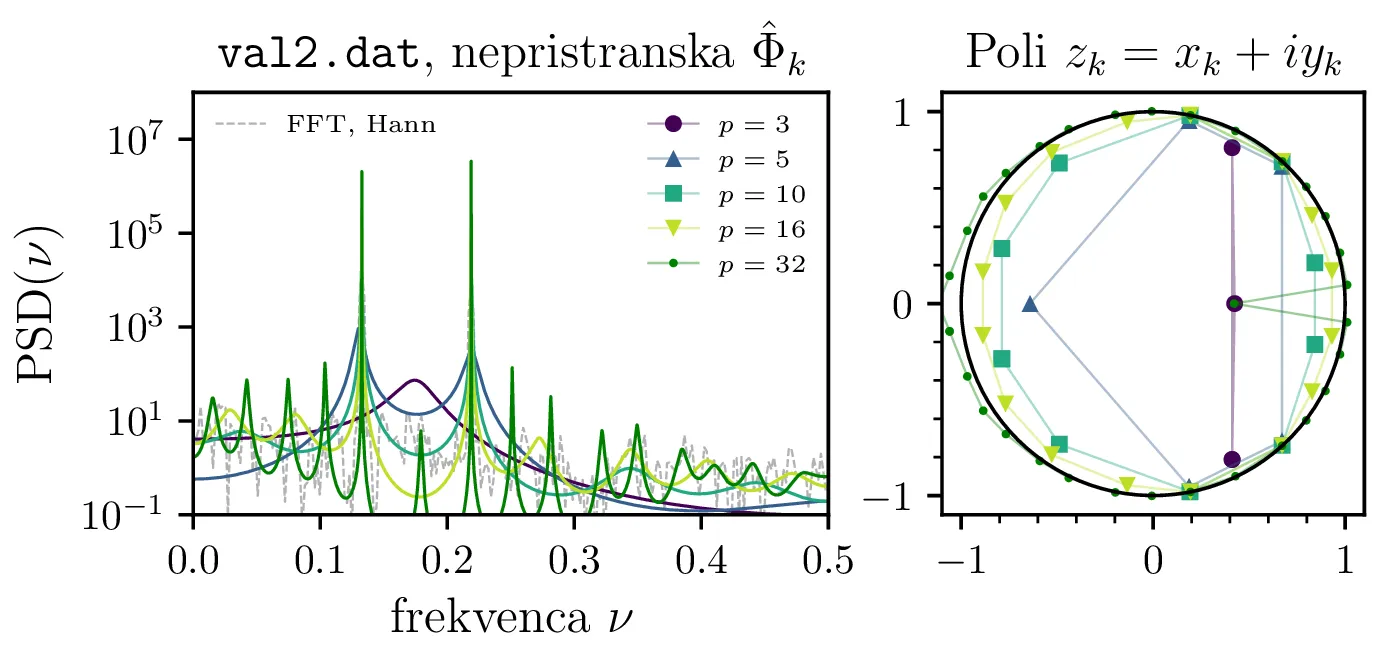
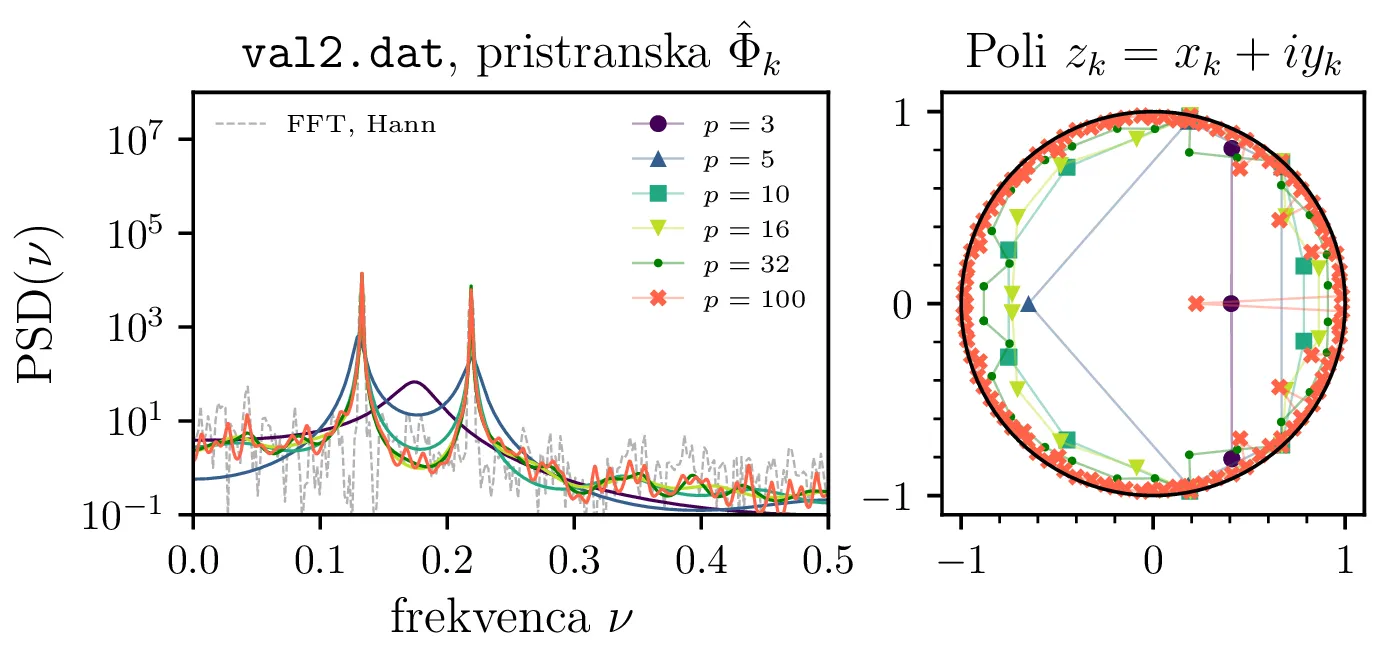
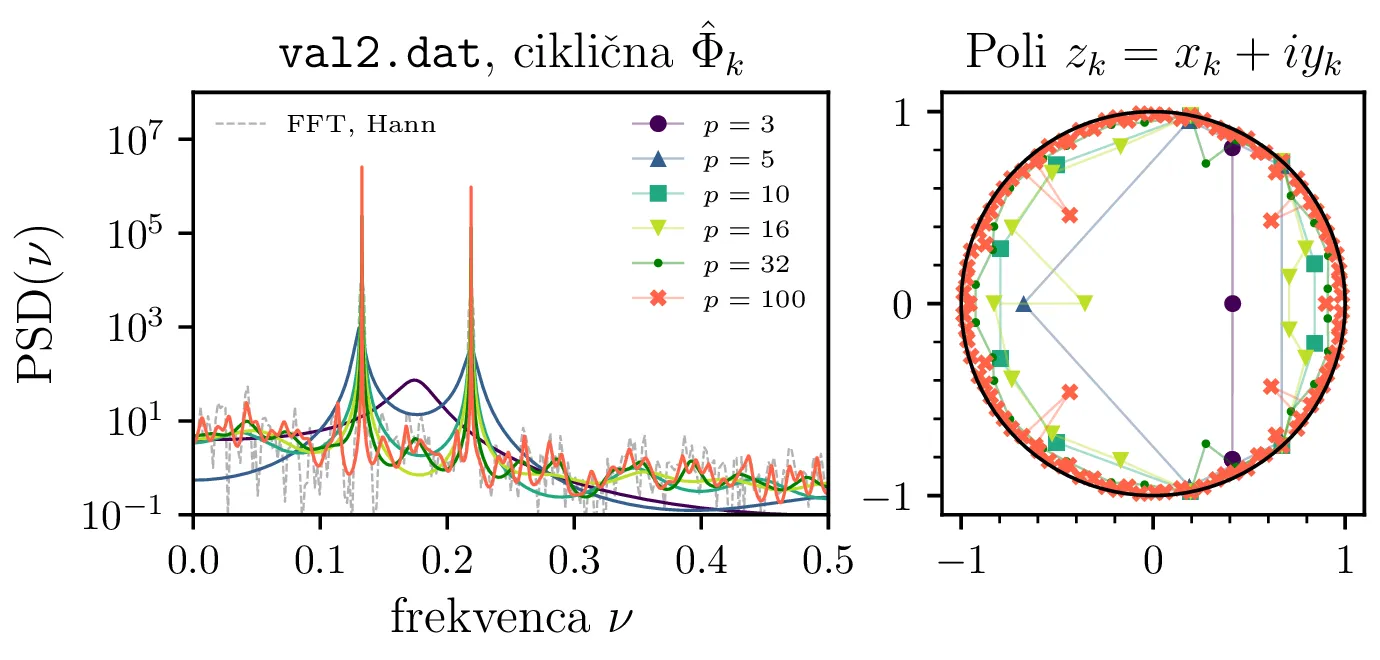
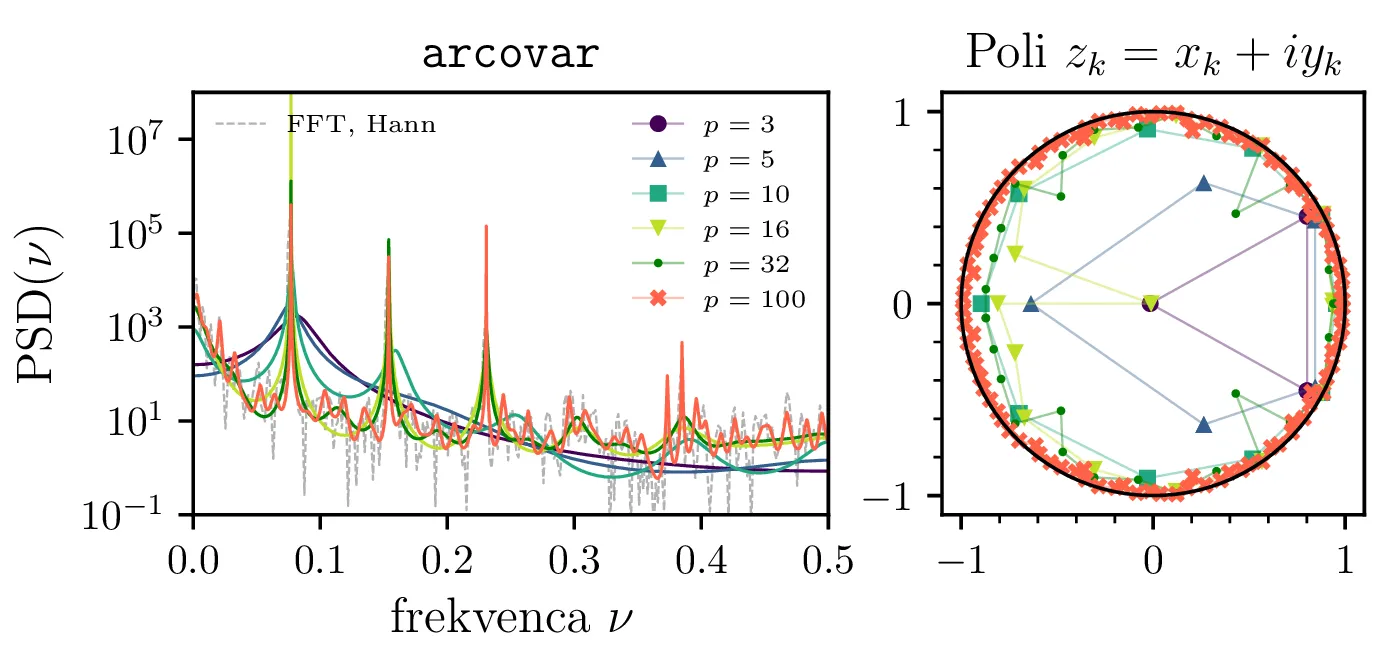
val2.dat. Avtoregresijsko koeficienti
so določeni po Yule-Walker metodi, pri čemer avtokorelacijo signala
\(\Phi_k\) ocenimo na tri različne načine, z nepristransko oceno 5, s pristransko oceno 6
in s ciklično avtokorelacijo 7. Narisana je spektralna moč
\(\mathrm{PSD}(\nu) = |H(z = e^{i2\pi\nu})|\) za avtoregresijske koeficiente
različnih redov. Vidimo, da z višanjem reda postanejo vrhovi spektra vedno bolj ostri, pri nepristranski oceni
avtokorelacije se začnejo pojavljati tudi novi vmesni vrhovi. Pripadajoče desno so za vsak spekter narisani
tudi poli prenosne funkcije \(\{z_k\}_k\).
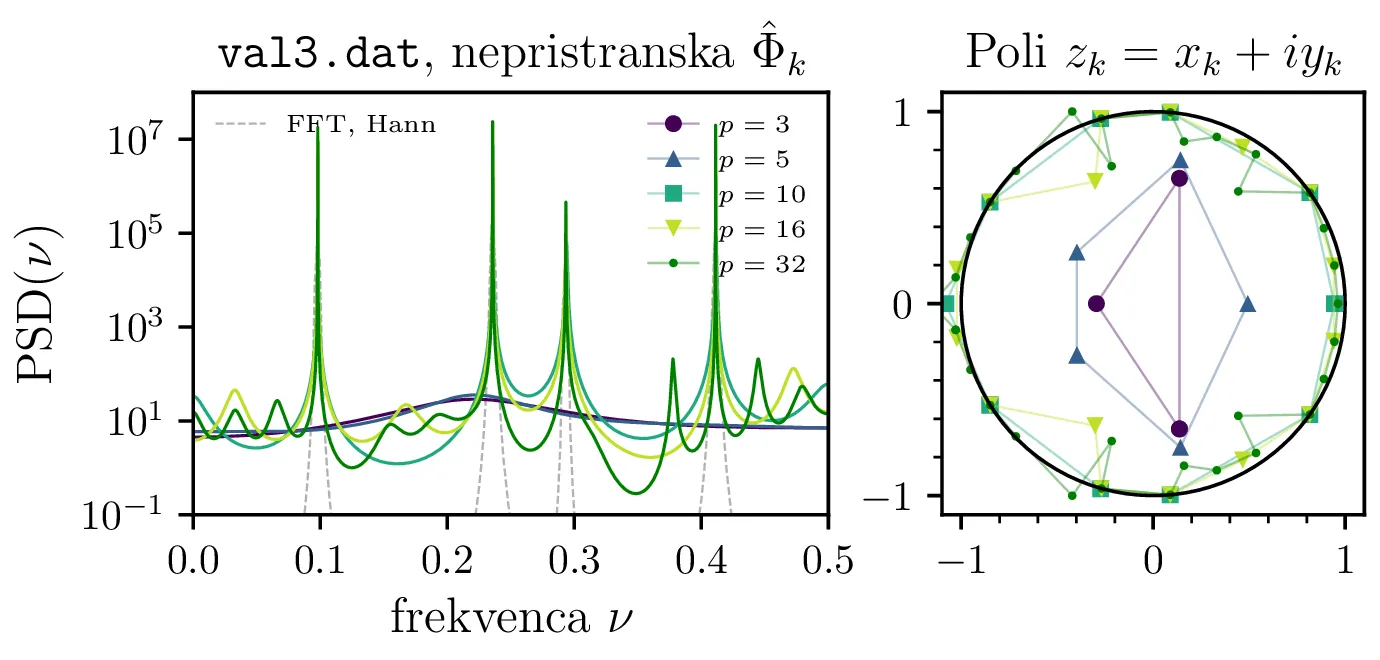
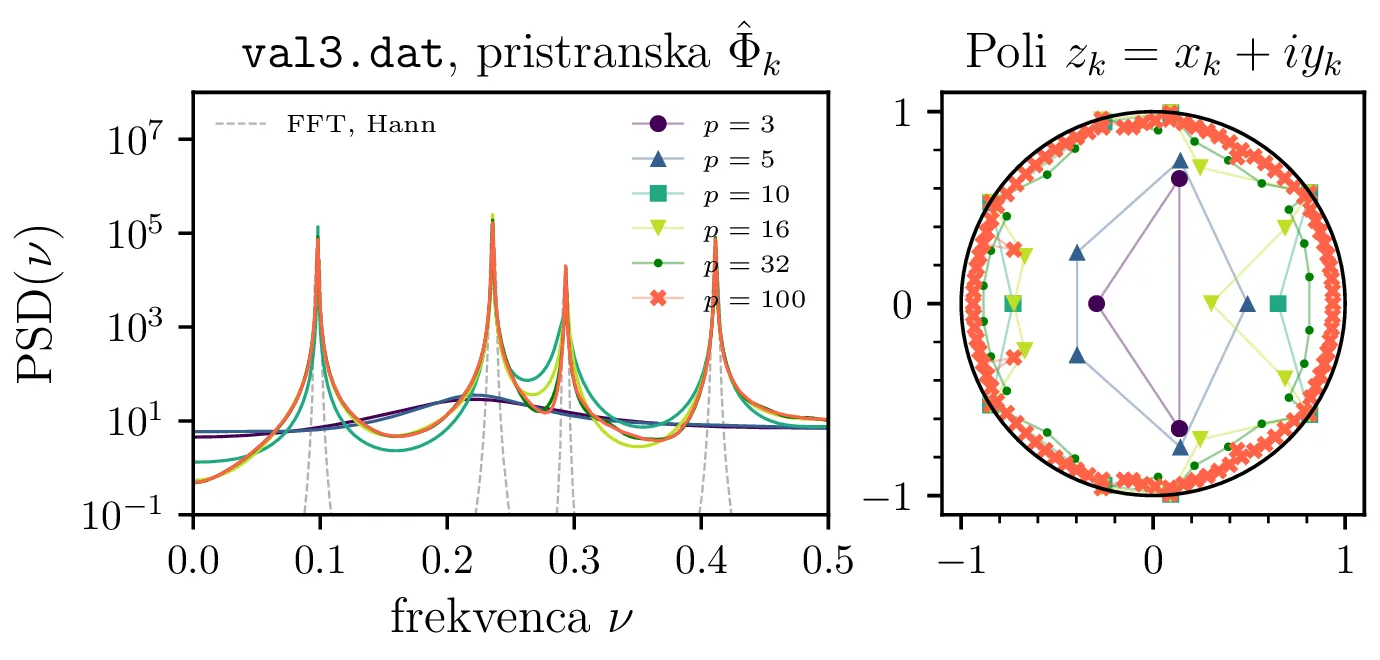
val3.dat. Glej opis slike 2.
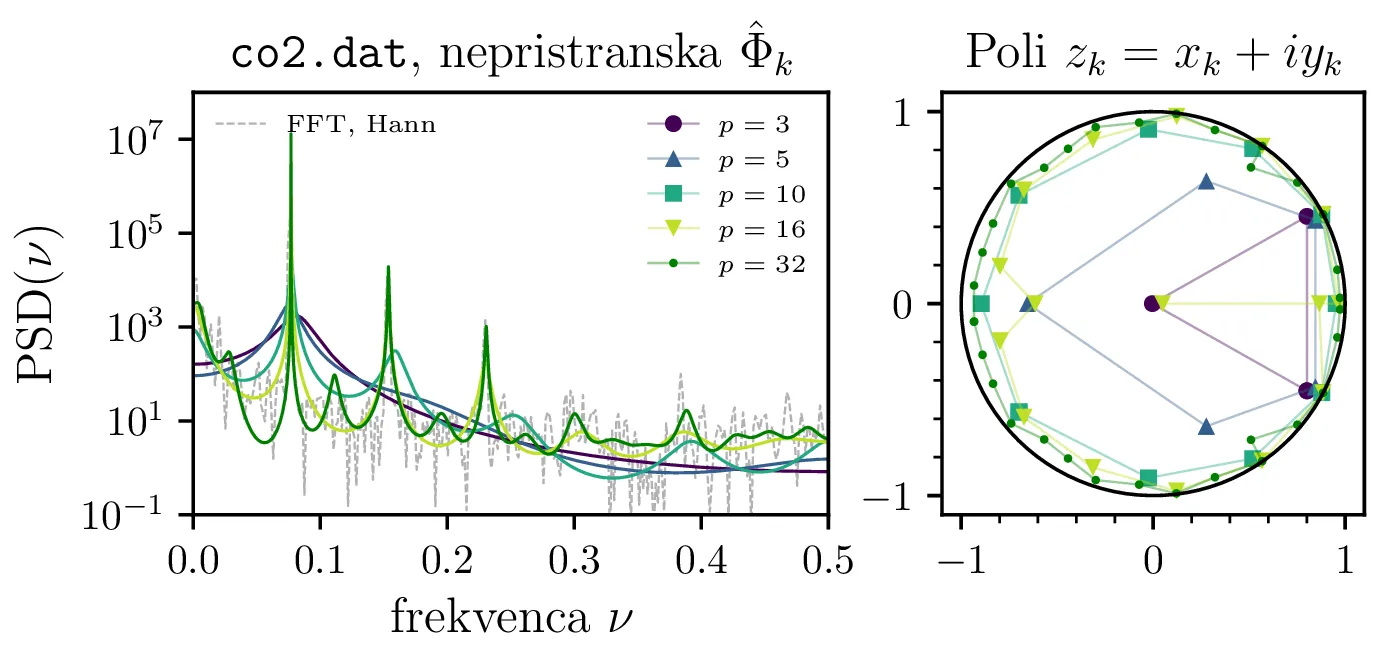
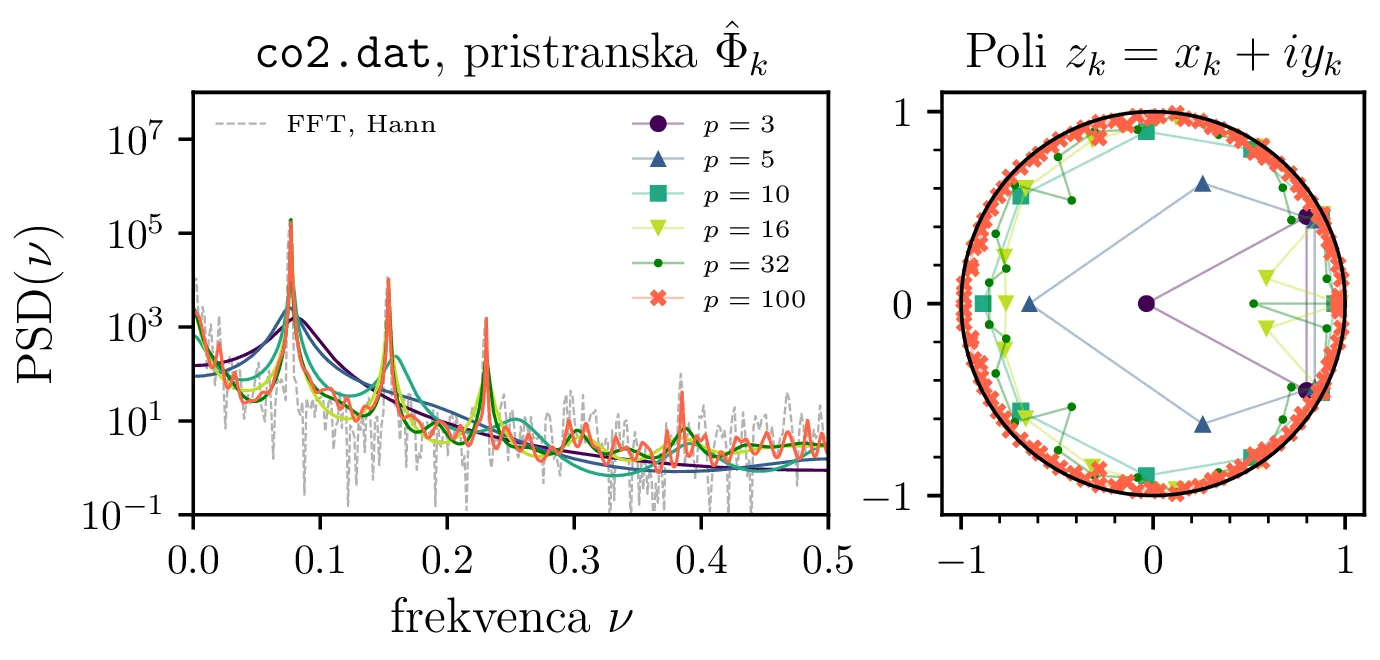
co2.dat. Glej opis slike 2.
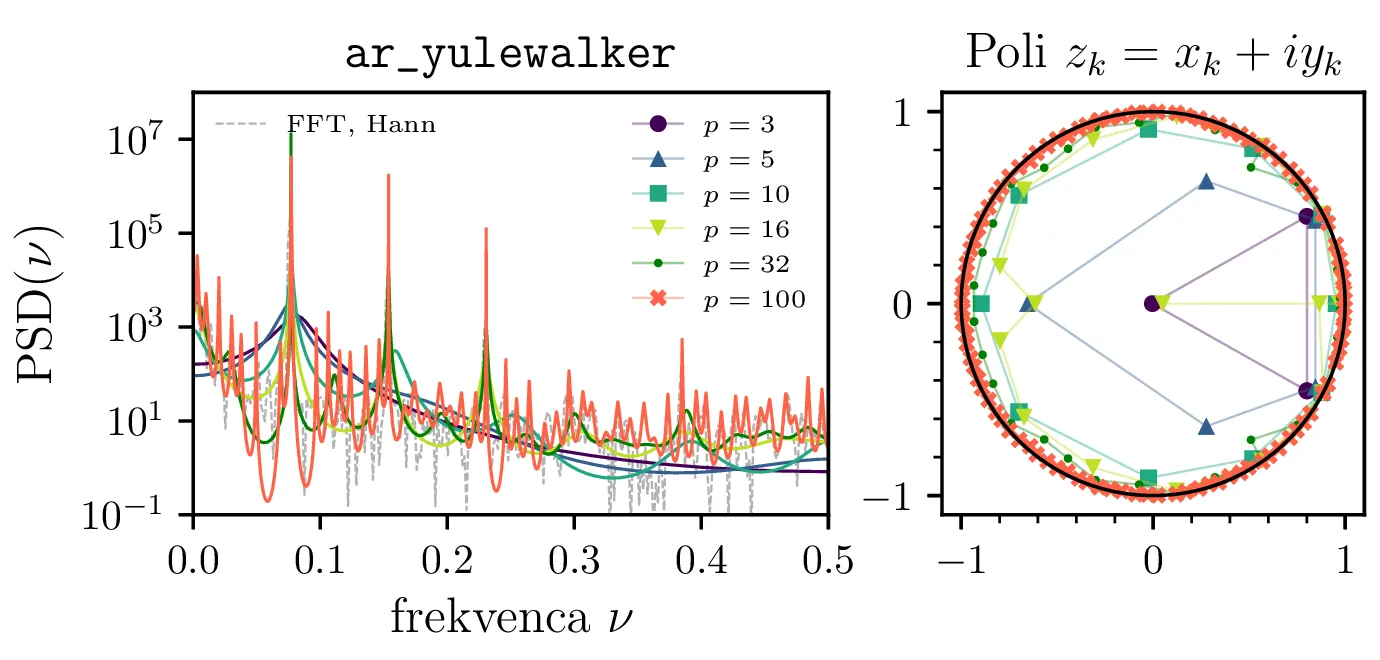
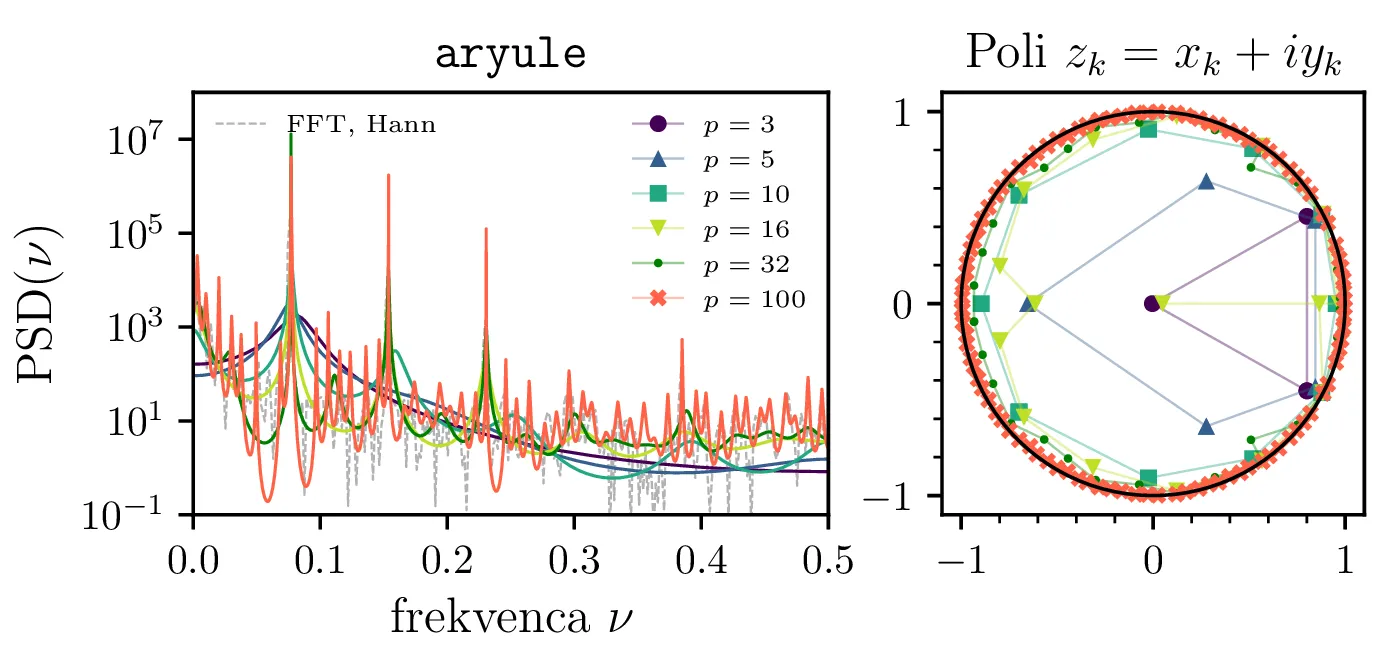
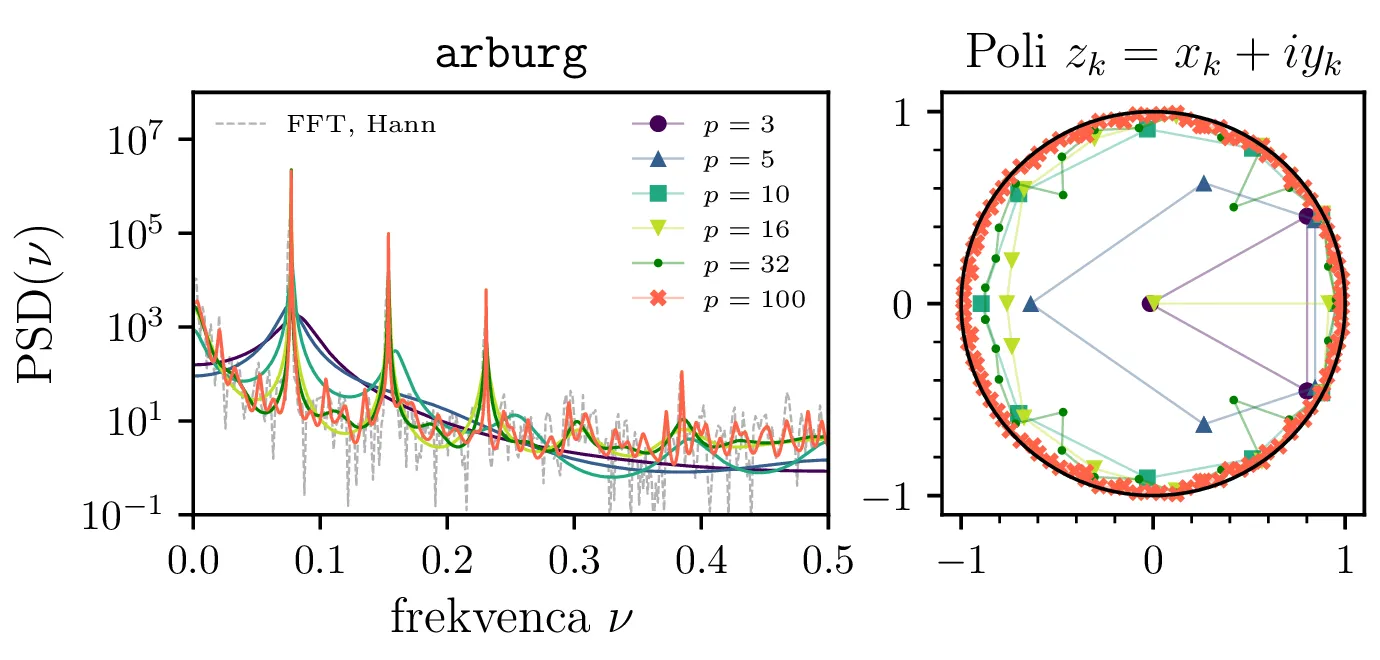
co2.dat. Metodi
ar_yulewalker in aryule sta obe rešujeta Yule-Walker sistem (nepristranska ocena
avtokorelacije), ar_yulewalker pa je lastna implementacije za primerjavo, aryule pa
je iz Python knjižnice Spectrum, tako kot tudi
metodi arburg in arcovar.
Ocena spektra po metodi maksimalne entropije
Če za nek linearni sistem poznamo avtoregresijske koeficiente \(\{ a_k \}_k\), nam njena prenosna funkcija ponuja informacijo o spektru sistema. Konkretno je spektralno gostoto moči za naš sistem kar \[\mathrm{PSD}(\nu) = \| H(z = e^{i2\pi \nu}) \|^2 = \left\| \frac{G}{1 + \sum_{k = 1}^{p} a_k z^{-k}} \right\|^2,\] pri čemer je tako spektralno moč potrebno razumeti kot oceno, sicer po metodi maksimalne entropije (ang. maximum entropy method ali MEM). Preden se posvetimo ocenam spektra za signale, lahko na kratko razložimo še en način, da avtoregresijske koeficiente \(\{ a_k \}_k\) dejansko izračunamo, t. j. Yule-Walkerjevo metodo. Če prihodnje izhode našega sistem napovedujemo kot \begin{equation}\hat{s}_n = - \sum_{k=1}^p a_k S_{n-k}, \label{eq:napoved}\end{equation} bo RMSE napaka naše napovedi \(\epsilon = E\left[ (s_n - \hat{s}_n)^2 \right]\). Proste parametre \(\{ a_k \}_k\) sedaj lahko optimiziramo tako, da bo RMSE napaka stacionarna \(\frac{\partial \epsilon}{\partial a_k} = 0\), iz česar (izpeljavo izpustimo) dobimo neskončni sistem enačb \begin{equation}\sum_{k=1}^p a_k E[s_{n-k} s_{n-i}] = - E[s_n s_{n-i}], \label{eq:normal-system}\end{equation} v katerem dvakrat nastopa avtokorelacija signala \(\Phi_i = E[s_{n} s_{n-i}] = \Phi(n, n-i)\), prvič na desni strani. Nekoliko drugače pa na levi pa kot \(E[s_{n-k} s_{n-i}]\), kjer imamo dva indeksa \(k, i\), a če je proces stacionaren (uporabna, ne nujno upravičena predpostavka), velja \(E[s_{n-k} s_{n-i}] = E[s_{n} s_{n-(i - k)}] = \Phi_{i - k}\). Za končen filter, kjer ima avtokorelacija končno podporo, se sistem enačb 3 prepiše v \[\sum_{k=1}^p a_k \hat{\Phi}_{i-k} = -\hat{\Phi}_i, \quad i = 1, 2, \dots, p,\] pri čemer smo avtokorelacijo zamenjali z njeno oceno \(\Phi_k \mapsto \hat{\Phi}_k\). Pomembno je tudi, da mora red biti nujno manjši od \(p \le N - 1\), pri čemer je \(N\) dolžina signala. Sistem enačb, t. j. Yule-Walkerjev sistem, zapišemo tudi v matrični obliki, ki jo lahko zaradi učinkovito izračunamo v \(\mathcal{O}(p^2)\), saj je matrika po obliki Toeplitzova – vzdolž diagonal je konstantna \begin{equation}\begin{bmatrix} \hat{\Phi}_{0} & \hat{\Phi}_{1} & \cdots & \hat{\Phi}_{p-1} \\ \hat{\Phi}_{1} & \hat{\Phi}_{0} & \cdots & \hat{\Phi}_{p-2} \\ \vdots & \vdots & \ddots & \vdots \\ \hat{\Phi}_{p-1} & \hat{\Phi}_{p-2} & \cdots & \hat{\Phi}_{0} \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_p \end{bmatrix} = - \begin{bmatrix} \hat{\Phi}_{1} \\ \hat{\Phi}_{2} \\ \vdots \\ \hat{\Phi}_{p} \end{bmatrix}. \label{eq:yulewalker}\end{equation} Koeficiente \(\{ a_k \}_k\) torej določimo tako, da izračunamo oceno avtokorelacije \(\Phi_k\), nato pa rešimo sistem 4. Pravzaprav je sistem enačb dovolj določen, da lahko izračunamo še zadnji prosti parameter \(G\), torej ojačitveni skalar filtra \(G^2 = \epsilon_{\min}^{(p)} = \hat{\Phi}_0 + \sum_{k=1}^p a_k \hat{\Phi}_k\).
Ocene spektrov izračunamo za signala val2.dat, val3.dat (slika 1
levo) in signal \(\mathrm{CO}_2\) koncentracije iz co2.dat, ki mu
odštejemo trend (slika 1
desno). Spektre \(\mathrm{PSD}(\nu)\) po metodi maksimalne entropije ocenimo z
uporabo Yule-Walkerjeve metode, sicer za tri različne načine izračuna avtoregresijskih koeficientov (slike 2, 3 in 4).
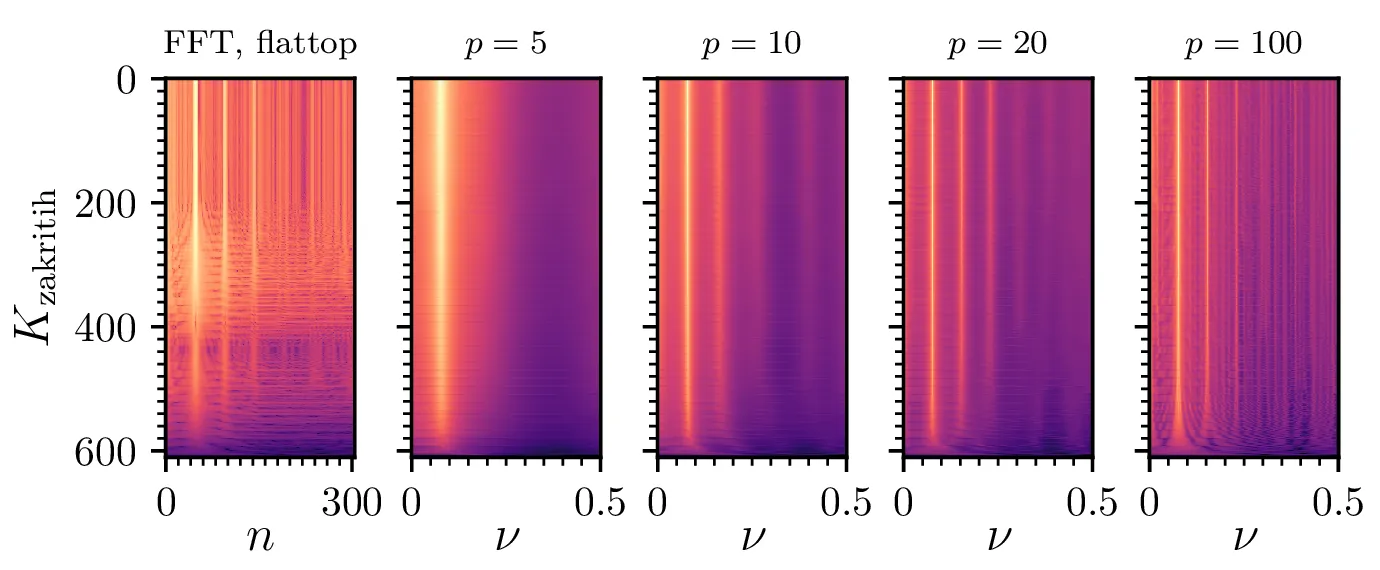
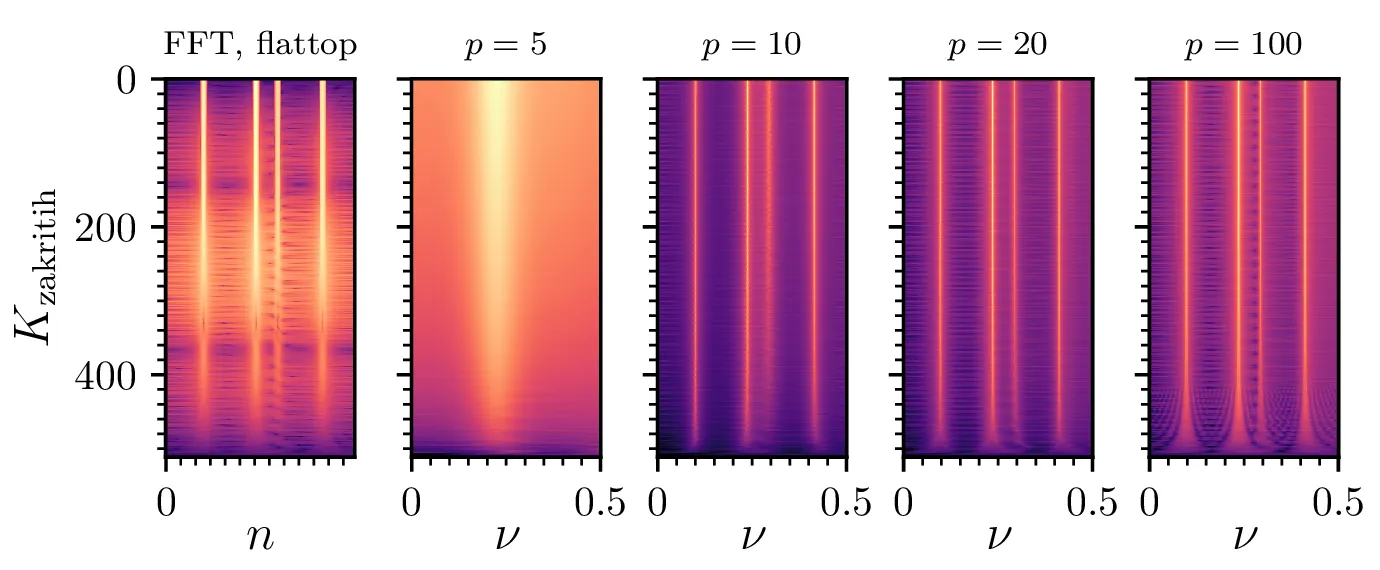
co2.dat, ki ima
\(611\) vzorcev, zakrijemo zadnjih
\(K_\mathrm{zakritih}\), nato pa izračunamo spekter. (Skrajno levo) Za
primerjavo, FFT spekter z flattop okensko funkcijo. (Desne štiri) MEM spektri za nekaj različnih redov.
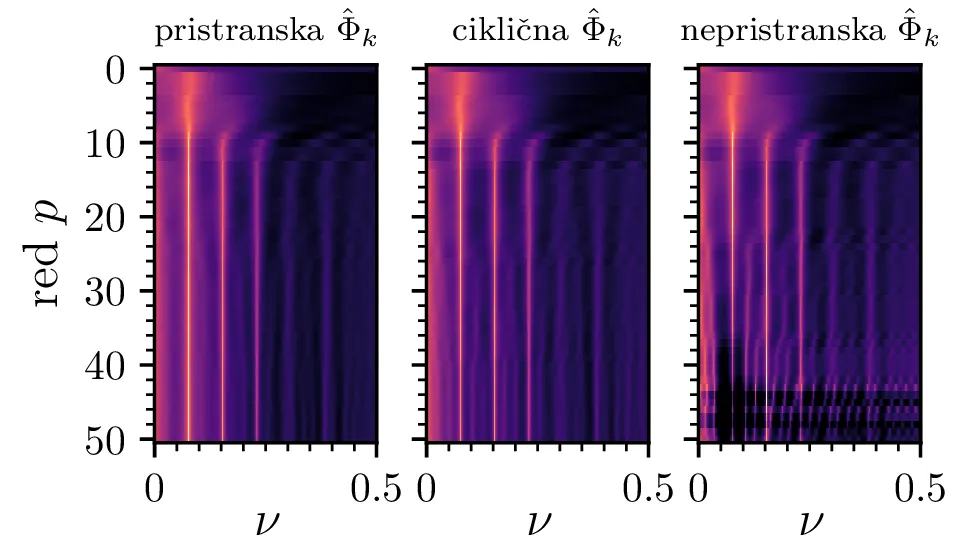
co2.dat. Vidimo, da je pri nizkih redih število prostih
parametrov premajhno, da bi lahko ujeli vse pomembne spektralne vrhove. Od leve proti desni lahko primerjamo
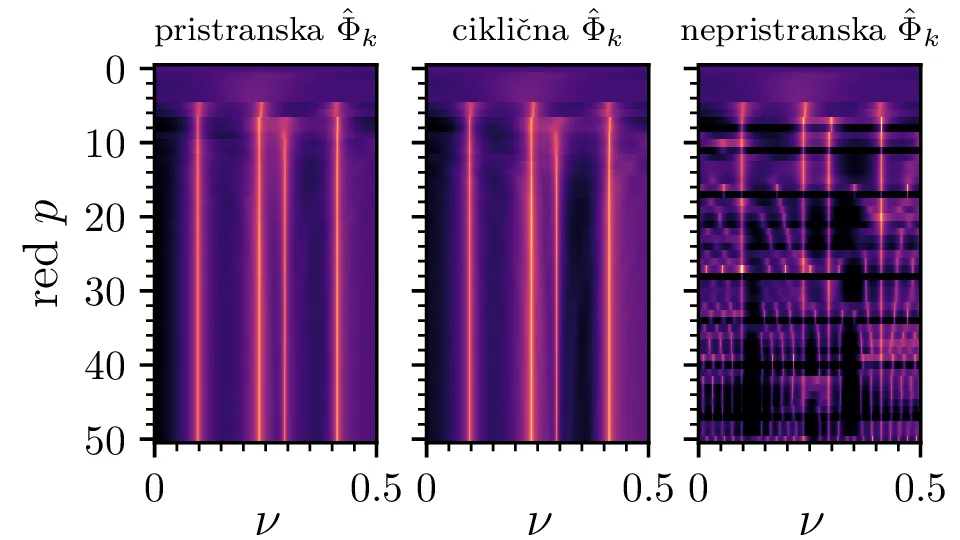
spektre z Yule-Walker metodo za različne ocene avtokorelacije
\(\hat{\Phi}_k\). Nepristranska ocena
\(\hat{\Phi}_k\) izkazuje precej patološko nestabilnost same metode; še bolj
izrazito se to vidi za signal val3 na sliki 9
spodaj. Ti artefakti so prisotni tako pri lastni implementaciji ar_yulewalker kot tudi pri
uporabi aryule iz paketa Spectrum, ki
pri tem vrne negativno varianco \(G^2\).
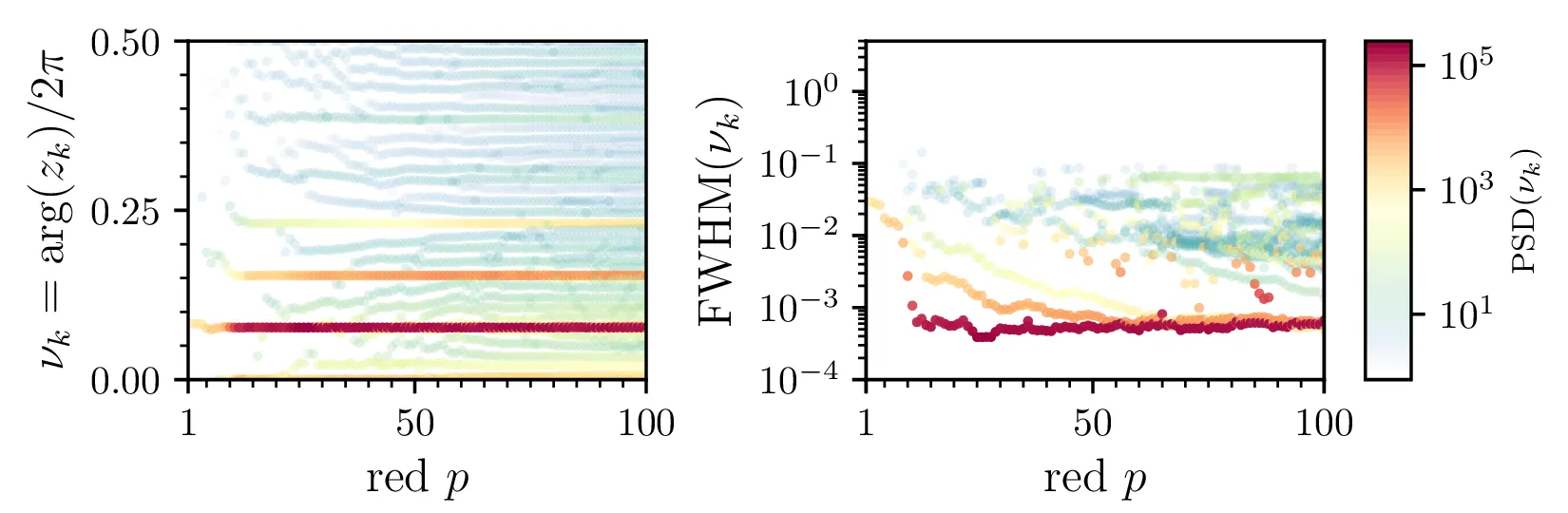
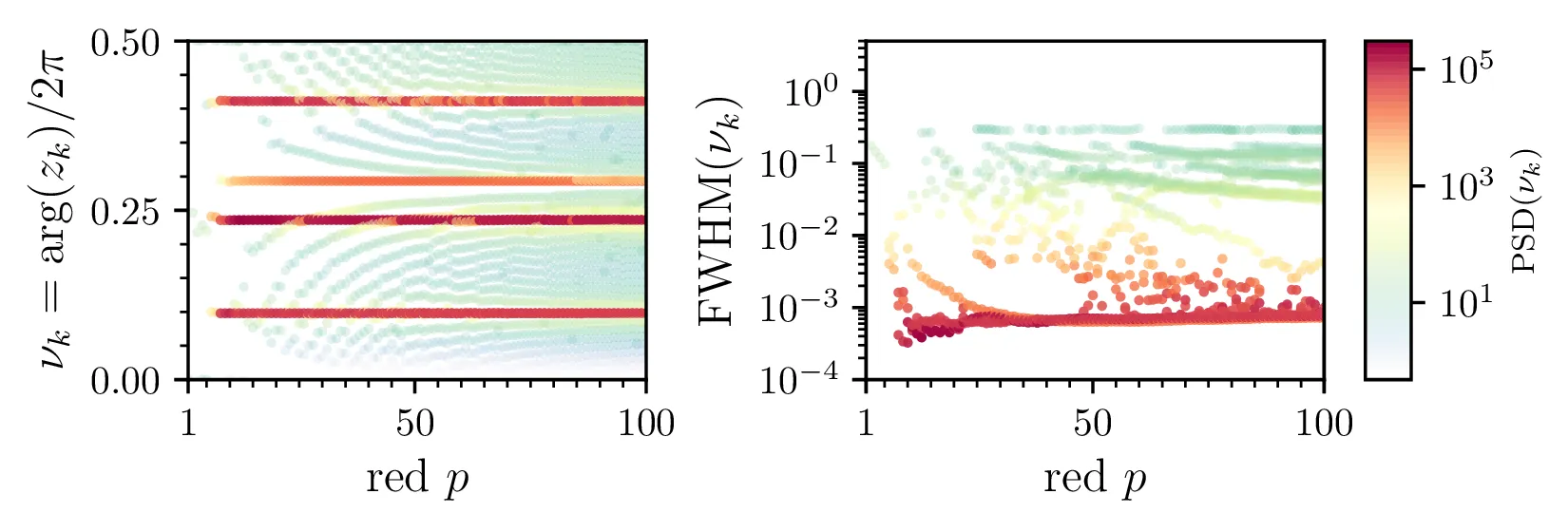
co2.dat. (Levo) Pozicije spektralnih vrhov
\(\nu_k = \frac{\mathop{\mathrm{arg}}(z_k)}{2\pi}\). Točke so obarvane glede
na amplitudo spektralne moči, ovrednotene na enotski krožnici
\(\mathrm{PSD}(\nu_k) = \left\| H\left( \frac{z_k}{|z_k|} \right) \right\|\).
(Desno) Spektralne širine, izračunane kot \(\mathrm{FWHM}\) spektra
\(\mathrm{PSD}(\nu)\) v okolici \(\nu_k\).
Vidimo, da z naraščanjem reda širine spektralnih črt padajo, nato pa se ustalijo v neko spodnjo mejo. Spekter
za izračun \(\mathrm{FWHM}\) je bil vzorčen v
\(5000\) točkah; vzorčenje v \(10^5\) točkah
ni opazno spremenilo spodnjega pragu spektralnih \(\mathrm{FWHM}\) širin
(\(\sim 0.4\cdot 10^3\)).
val3.dat. (Zgoraj) Vpliv odstranjevanja vzorcev na MEM oceno spektra. (Sredinska
vrstica) Vpliv reda na MEM oceno spektra. (Spodaj) Pozicije in širine spektralnih vrhov za naraščajoč red
\(p\).
Različni načini izračuna avtokorelacije
Pomembna izbira pri reševanju Yule-Walkerjevega sistema 4 je tudi način, kako ocenimo avtokorelacijo. Prvi način je nepristranska (ang. unbiased) ocena, kjer faktor \(\frac{1}{N - k}\) kompenzira za vedno krajši signal \begin{equation}\hat{\Phi}_k = \frac{1}{N - k} \sum_{i = k}^{N - 1} s_i s_{i - k}, \quad\text{nepristranska ocena}, \label{eq:acorr_unbiased}\end{equation} primerjamo jo z pristransko oceno, kjer imamo namesto faktorja \(\frac{1}{N - k}\) prisoten le faktor \(\frac1N\), sicer \begin{equation}\hat{\Phi}_k = \frac{1}{N} \sum_{i = k}^{N - 1} s_i s_{i - k}, \quad\text{pristranska ocena}. \label{eq:acorr_biased}\end{equation} Kot tehnično opombo omenimo še tretji način izračuna, tako imenovano periodično avtokorelacijo (ang. circular autocorrelation), kjer smatramo, da je signal periodičen. Taka različica avtokorelacije je zanimiva, ker jo po konvolucijskem izreku lahko izrazimo kot produkt v frekvenčni domeni \begin{equation}\hat{\Phi}_k = \frac{1}{N} \sum_{i = 0}^{N - 1} s_i s_{(i - k) \bmod N} = \mathop{\mathrm{DFT}^{-1}} \left\{ S_n S_n^\ast \right\}, \quad S_n = \mathop{\mathrm{DFT}} \{ s_k \}. \label{eq:acorr_cyclic}\end{equation} Preko te identitete in uporabe hitre Fourierove transformacije (ang. FFT) lahko izračunamo tudi prvi dve vrsti ocen avtokorelacije 5, 6.
Na sliki 2 primerjamo tri različne načine za izračun oz. oceno avtokorelacije. Vidimo, da spektri preko nepristranske ocene \(\hat{\Phi}_k\) pri višjih redih \(p\) postanejo prekomerno "špičasti", vsebujejo mnogo vmesnih vrhov, ki se ne pojavijo z pristransko oceno \(\hat{\Phi}_k\). Za oceno spektra je torej pristranska ocena avtokorelacije bolj robustna izbira. Ciklična avtokorelacija se obnaša izjemno podobno, a je v nadaljevanju ne uporabljamo.
Na vseh slikah MEM ocen spektrov so narisani tudi položaji polov prenosne funkcije. Jasno opazimo, da so poli \(\{z_k\}_k\) nastopajo v konjugiranih parih, saj so za realen signal avtoregresijski koeficienti \(\{ a_k \}_{k = 1}^{p} \in \mathbb{R}\). Nekateri poli so izven enotske krožnice (npr. slika 9 levo), a za ocene spektrov je to brez pomena, saj smo pri vrednotenji stalno na enotski krožnici \(z = e^{i2\pi \nu}\).
Alternative Yule-Walkerjevi metodi
Da sem se prepričal, da je pojavljanje vmesnih vrhov v ocenah
\(\mathrm{PSD}(\nu)\) zares lastnost Yule-Walkerjeve metode (in uporabe
nepristranske ocene za avtokorelacijo 5), sem na sliki 5 primerjal lastna
implementacija ar_yulewalker in aryule – implementacijo Yule-Walkerjeve metode, ki je
na voljo v Python paketu Spectrum. Poleg
Yule-Walkerjeve Poleg Yule-Walkerjeve metode in dveh (oz. treh) načinov za izračun avtokorelacije obstaja še
nekaj drugih metod za izračun avtoregresijskih koeficientov. Na sliki 5
sta za signal val2 narisana še Burgova arurg in kovariančna metoda
arcovar iz paketa Spectrum. Ti dve metodi sta robustni, pri višjih redih se ne začnejo pojavljati
močni vmesni vrhovi, temveč je prisotna le nekakšna modulacija. V kombinaciji s priporočili iz literature [1], kjer je Burgova metoda izpostavljena kot primernejša od Yule-Walkerjeve, to še dodatno potrjuje, da so vmesni
vrhovi patologija Yule-Walkerjeve metode z nepristransko oceno
\(\hat{\Phi}_k\).
Vpliv reda in števila meritev na oceno spektra
Na sliki 6
vidimo vpliv upoštevanega števila vzorcev co2.dat na ocene spektra, za nekaj različnih redov
avtoregresije. Preko primerjave z FFT spektrom na isti sliki levo lahko vidimo, da so MEM ocene spektrov precej
odporne na manjše število meritev, FFT spekter se začne spreminjali že ko odstranimo dobro polovico meritev,
medtem kot MEM spekter ostane enak nekje do \(4/5\) odstranjenih meritev.
Zanimivo je tudi videti, kako spekter konvergira, ko višamo red MEM ocen, kar lepo vidimo za
\(\mathrm{CO}_2\) signal na sliki 7; tu opazimo tudi numerično nestabilnost Yule-Walkerjeve metode, ko uporabljamo nepristransko oceno
avtokorelacije (glej referenco [1]). Še bolj nazorna je slika 8, kjer so narisani vsi poli, obarvani tako, da so bolj vidni tisti z višjimi amplitudami. Na sliki 8
desno vidimo tudi širine spektralnih vrhov, ki jasno padejo in se ustalijo pri zadostno visokih redih
\(p\). Vse slike 6, 7 in 8
narišemo tudi za signal val3, na sliki 9. Tu je v sredinski vrstici desno še bolj jasna numerična nestabilnost Yule-Walkerjeve metode z nepristransko
oceno avtokorelacije.
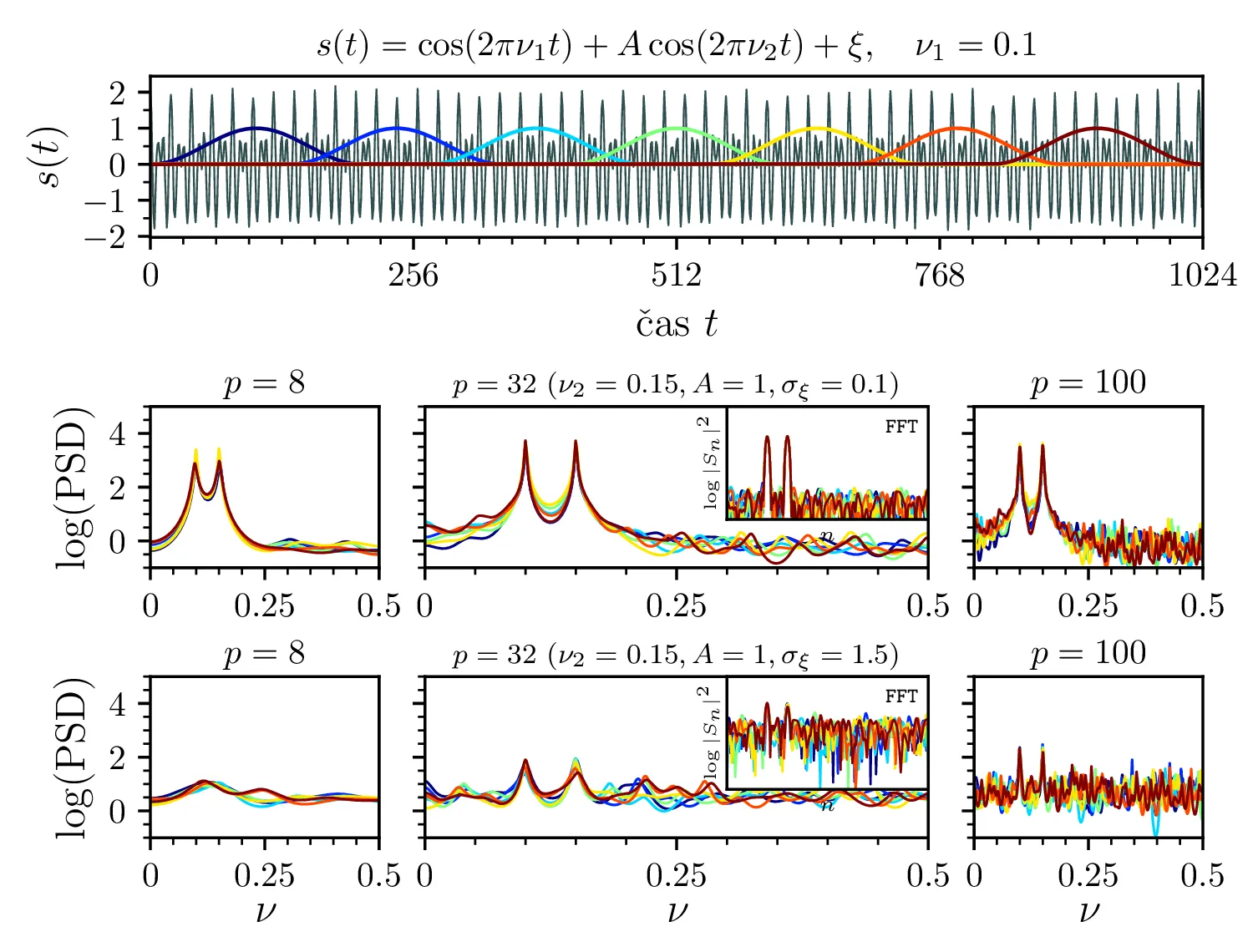
Vpliv šuma in ločljivosti spektralnih vrhov
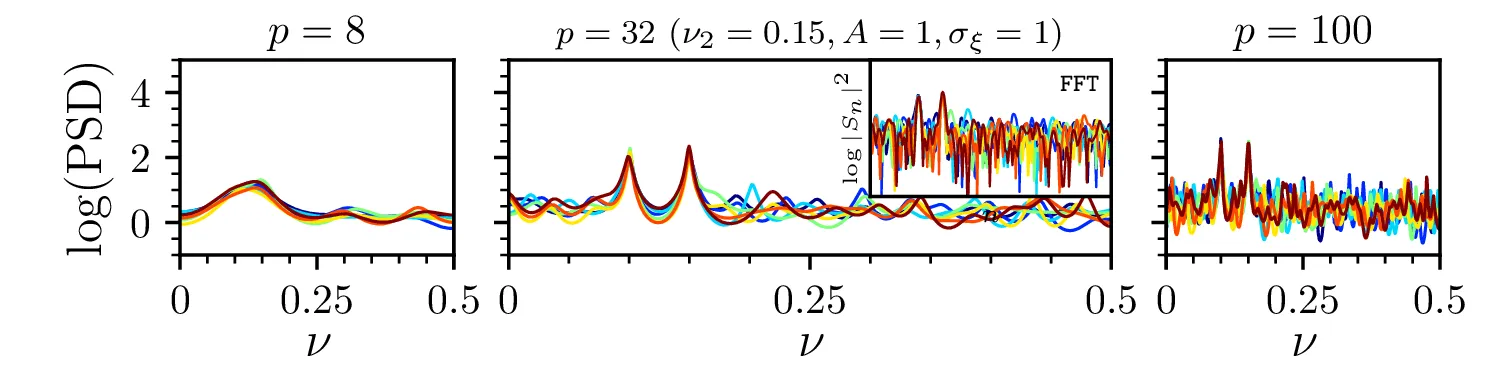
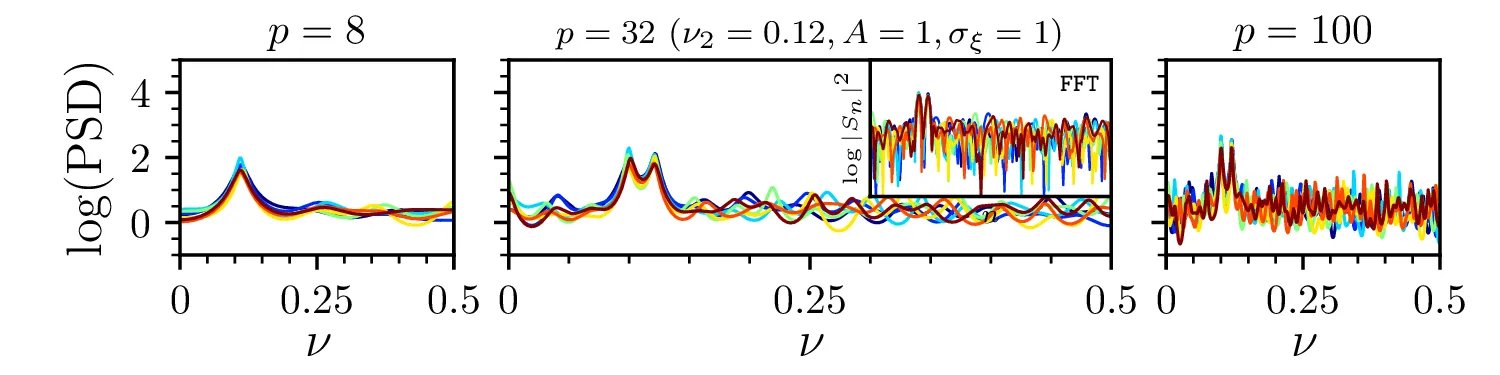
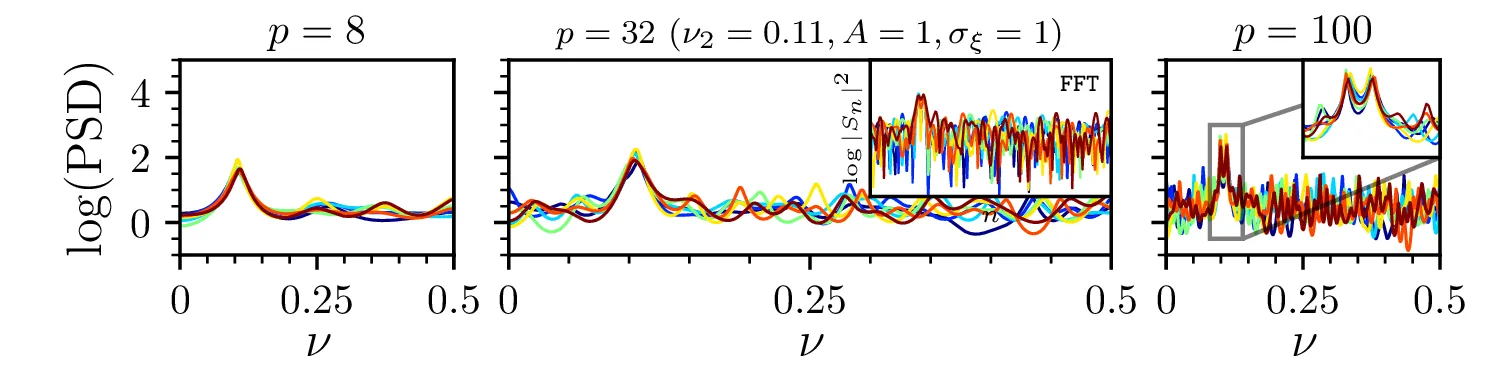
Metodo MEM preizkusimo še na testnem signalu z frekvenco \(\nu_1 = 0.1\) in drugo frekvenco \(\nu_2\) \[s(t) = \cos(2\pi \nu_1 t) + A \cos(2\pi \nu_2 t) + \xi, \quad \nu_1 = 0.1\] pri čemer je \(\xi\) Gaussovski šum z varianco \(\sigma_\xi^2\). Na sliki 10 vidimo vpliv dodanega Gaussovskega šuma na MEM oceno spektra testne funkcije \(s(t)\), ko okno drsi skozi signal. Pri višji amplitudi šuma je jasno, da je iz MEM ocene spektra vrhove lažje določiti kot iz FFT spektra. Na sliki 11 vidimo približevanje in zlivanje spektralnih vrhov. Ko je razlika v frekvenci majhna (spodnja vrstica, \(\nu_2 = 0.11\)), nizki redi \(p\) vrhov ne razločuje več, za višje rede (npr. \(p = 100\)) pa sta vrhova še vedno jasno ločljiva.
Linearna napoved
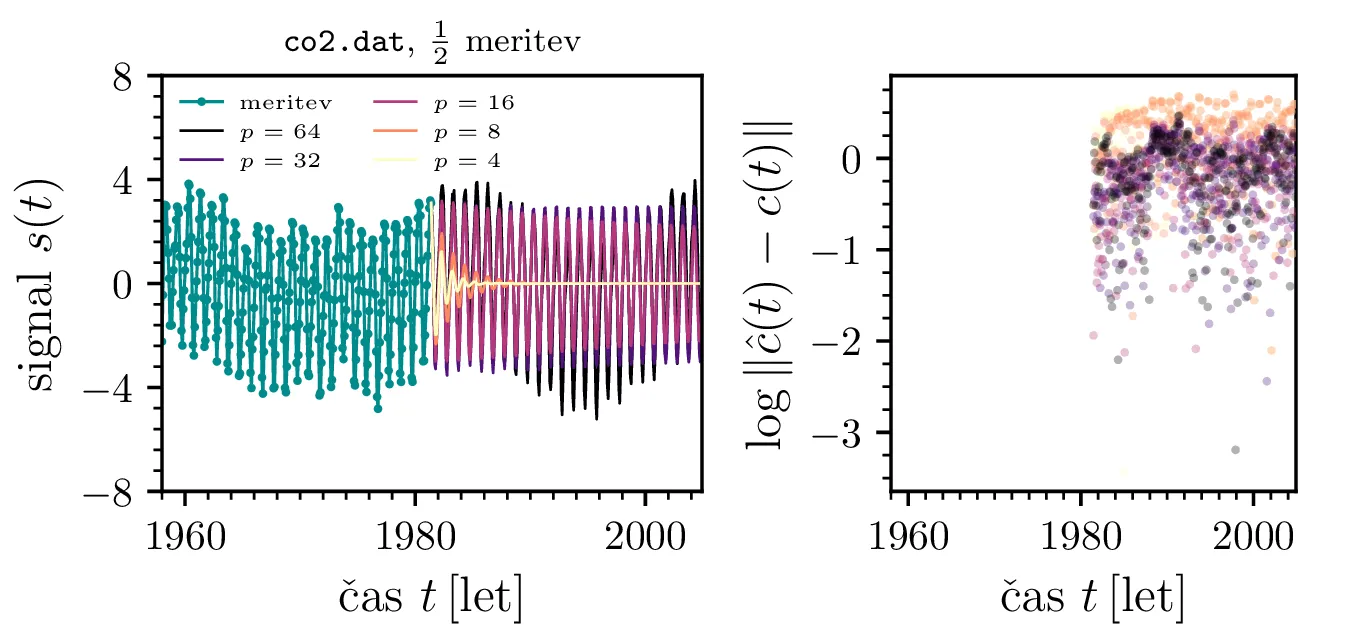
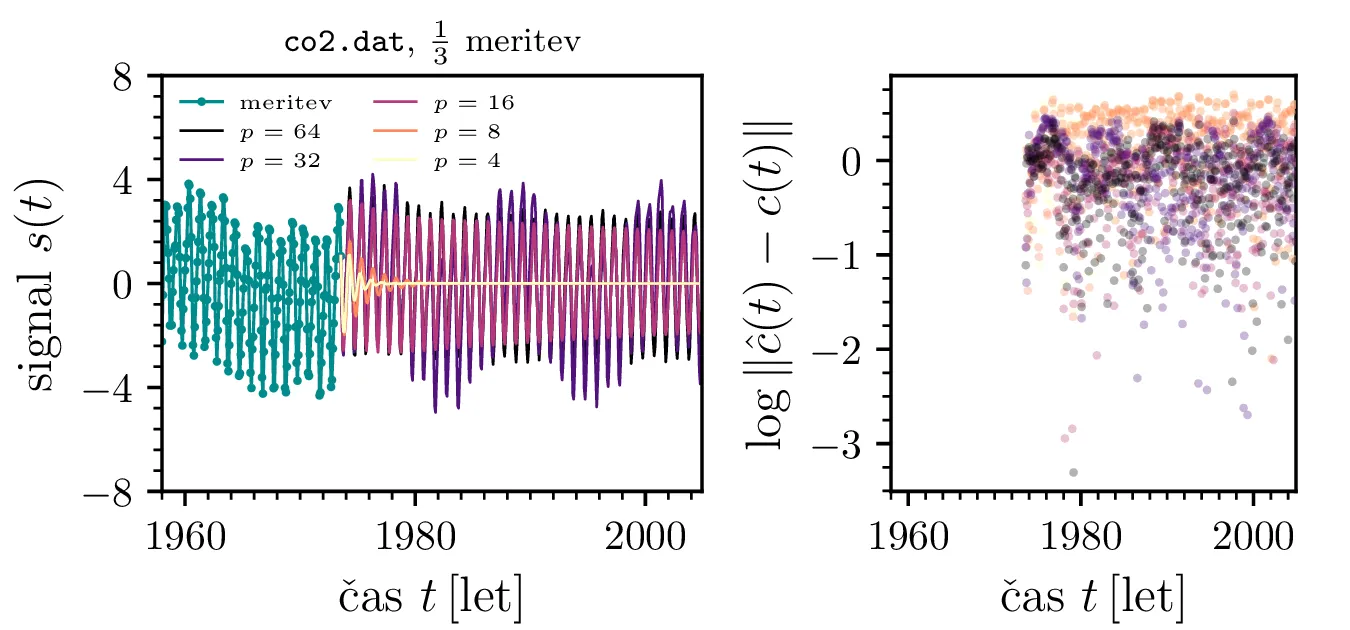
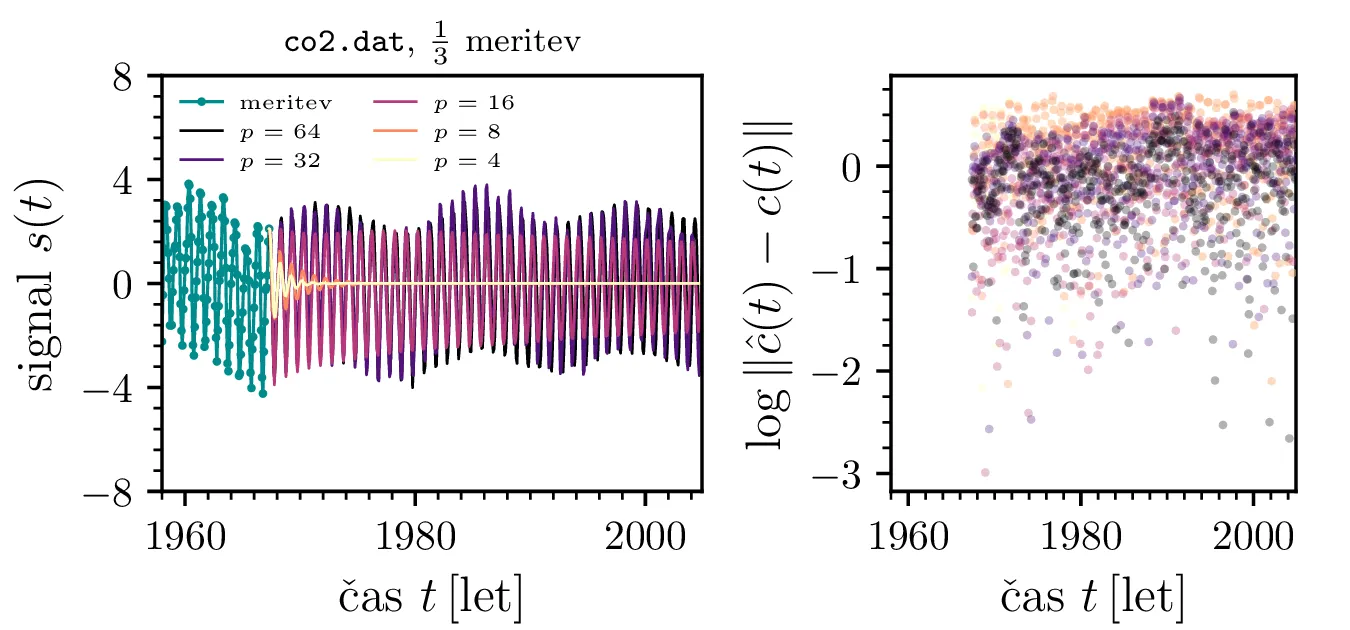
Zdaj izračunane avtoregresijske koeficiente \(\{ a_k \}_k\) uporabimo za napoved (sicer kot v 2) zakritih delov signala. Na sliki 12 je prikazana linearna napoved (Yule-Walkerjeva metoda z nepristransko oceno \(\hat{\Phi}_k\)) in njeno odstopanje od dejanskega, zakritega signala za koncentracijo \(\mathrm{CO}_2\) na podlagi \(1/2\), \(1/3\) in \(1/5\) meritev. Vidimo, da je napovedi postajajo boljše z višanjem reda, a le do neke mere.
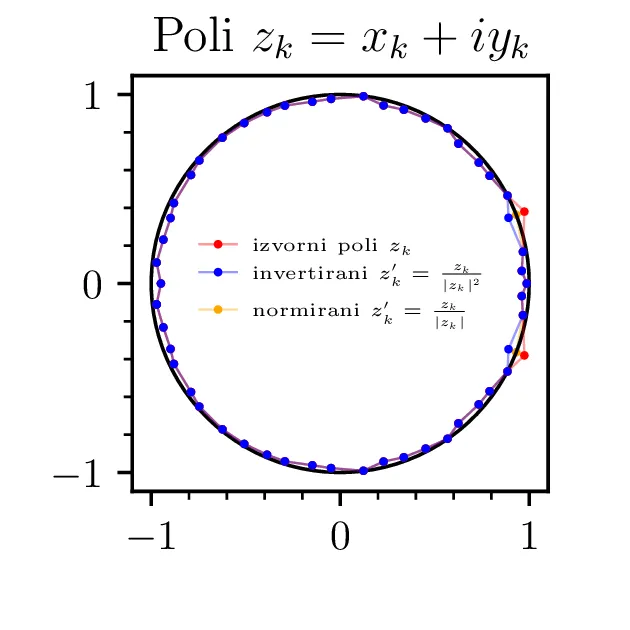
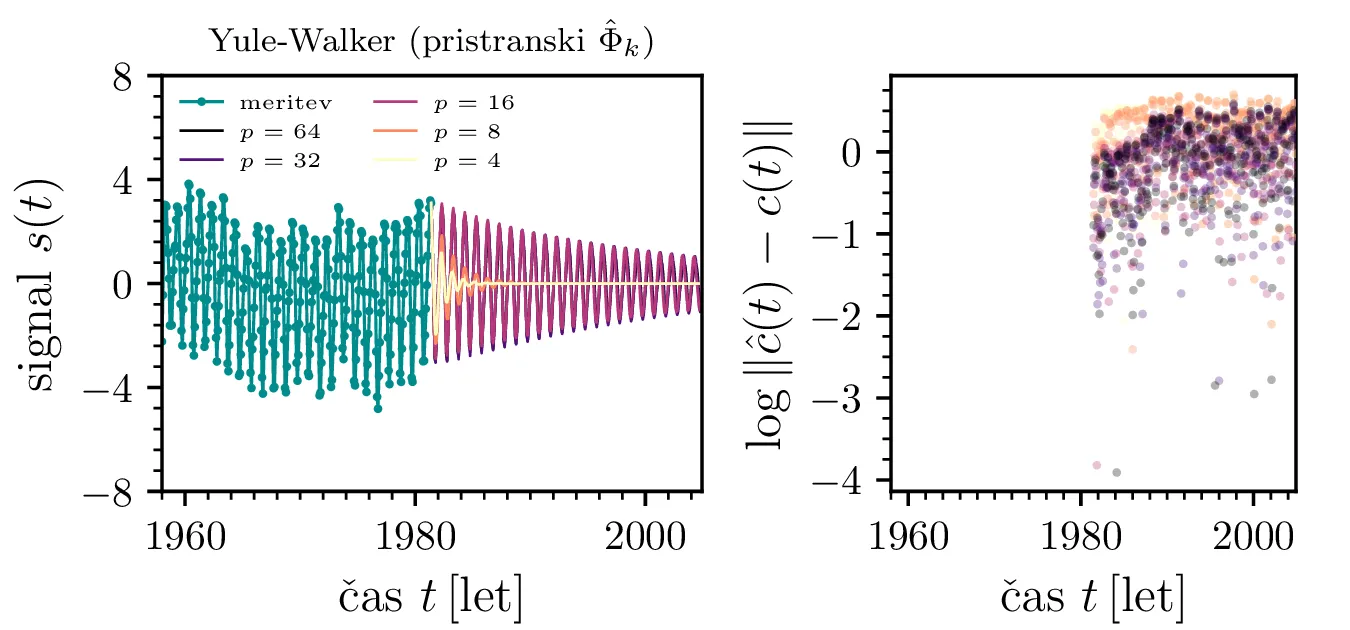
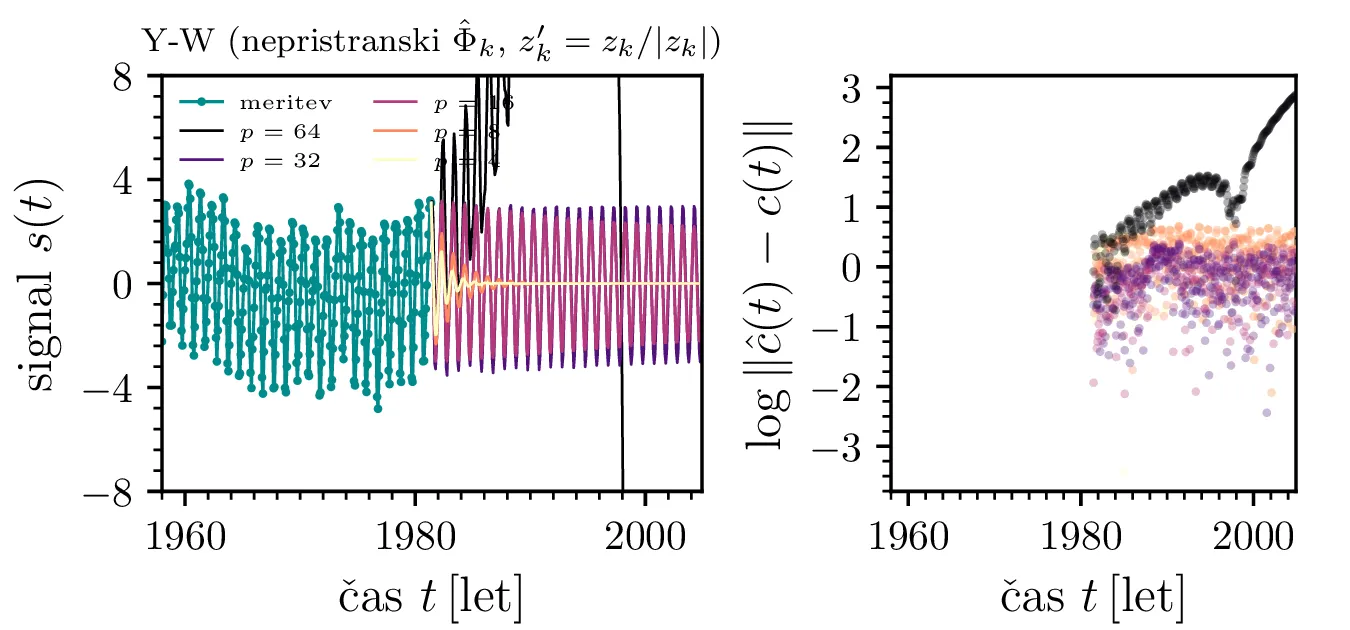
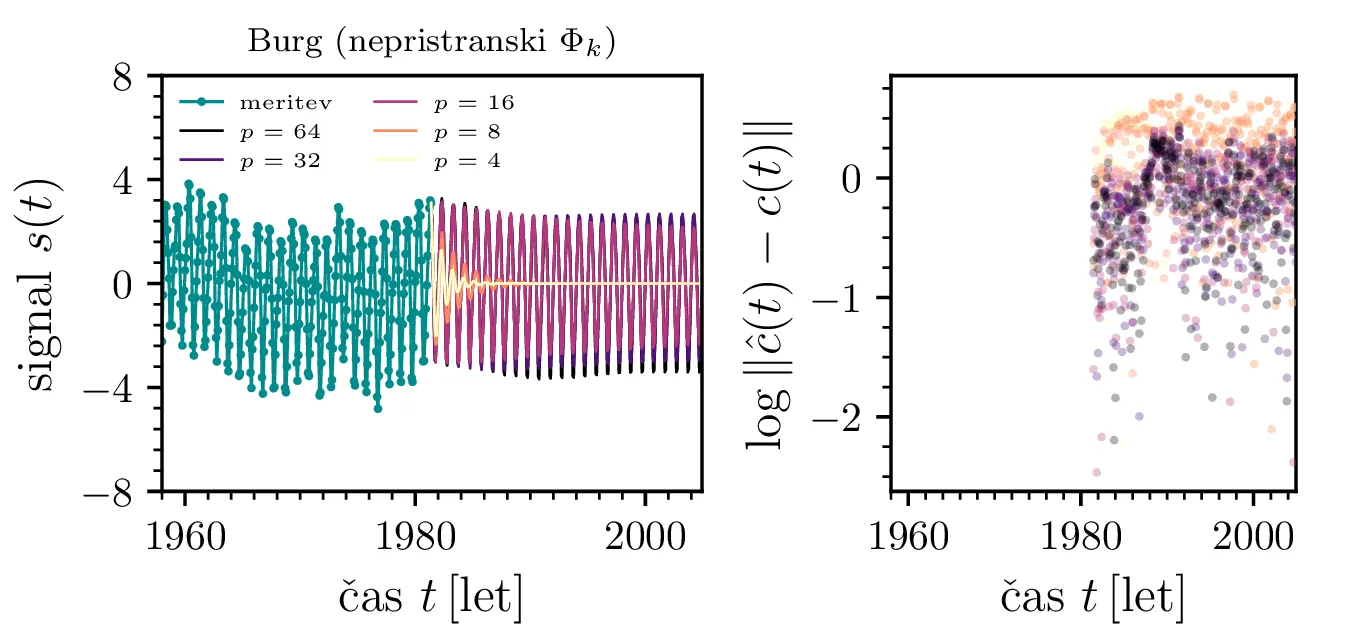
Yule-Walkerjeva metoda nam lahko vrne prenosno funkcijo, katere poli ležijo izven \(|z| \le 1\). To povzroči, da je filter nestabilen in napoved s časom raste preko vseh mej. Stabilnost zagotovimo z ročnim popravkom; skrajno desno zgoraj na sliki 12 vidimo pole za avtoregresijo reda \(p = 50\) in popravljene pole \(|z_k| > 1\), invertirane v notranjost enotske krožnice kot \(z_k' = \frac{z_k}{|z_k|^2}\). Takšno popravljanje polov je nekoliko ad hoc, zato obstajajo alternativne metode, kot je npr. Burgova, ki same po sebi zagotovijo stabilnost, torej da so vsi poli \(|z_k| \le 1\) že brez dodatnega popravljanja. Na sliki 13 vidimo alternativne načine za linearno napoved, kjer vidimo, da pristranska ocena \(\hat{Phi}_k\) porodi slabšo, močno upadajočo napoved. Na sredinski sliki 13 vidimo, da popravljanje polov z normiranjem \(z_k' = \frac{z_k}{|z_k|^2}\) namesto z inverzijo zares ne zagotovi stabilnosti, napoved še vedno nekontrolirano raste (verjetno zaradi numeričnih napak). Na desni sliki 13 pa vidimo, da je Burgova metoda stabilna tudi brez popravljanja polov, kar je velika prednost, saj ni potrebno uvesti nekega ad hoc postopka inverzije polov.
Vpliv reda na napako napovedi
Poleg časovnih potekov odstopanj napovedi, ki smo jih risali na sliki 12, lahko kakovost napovedi ocenimo kar sim skupnim RMSE odstopanjem med napovedanim in dejanskim signalom. Na sliki 14 vidimo odvisnost RMSE odstopanj od reda metoda, kjer je očiten izrazit padec RMSE napake, ko dosežemo zadosten red \(p\). Vidimo tudi, da različne metode izračuna avtoregresijskih koeficientov dajejo različno dobre napovedi, najbolj neprimerna, z izrazito največjo RMSE napako pa je Yule-Walkerjeva metoda z pristransko oceno \(\hat{\Phi}_k\), za katero smo že na sliki 13 levo videli, da podaja prekomerno upadajočo napoved.
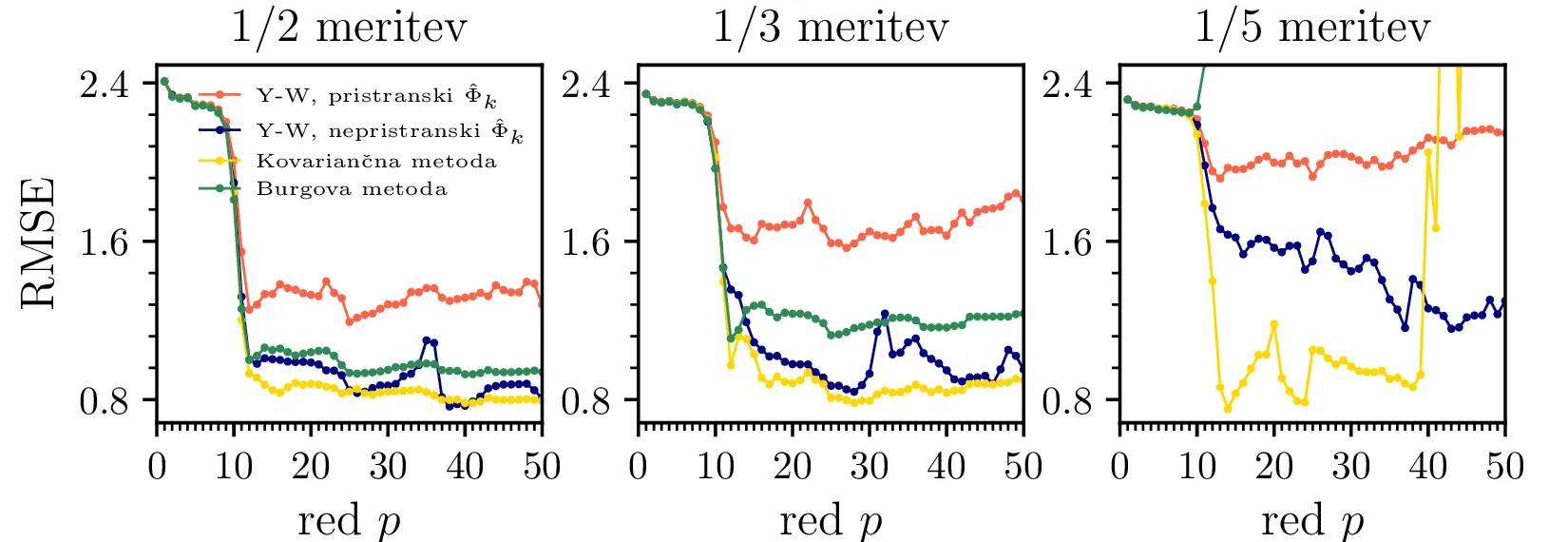
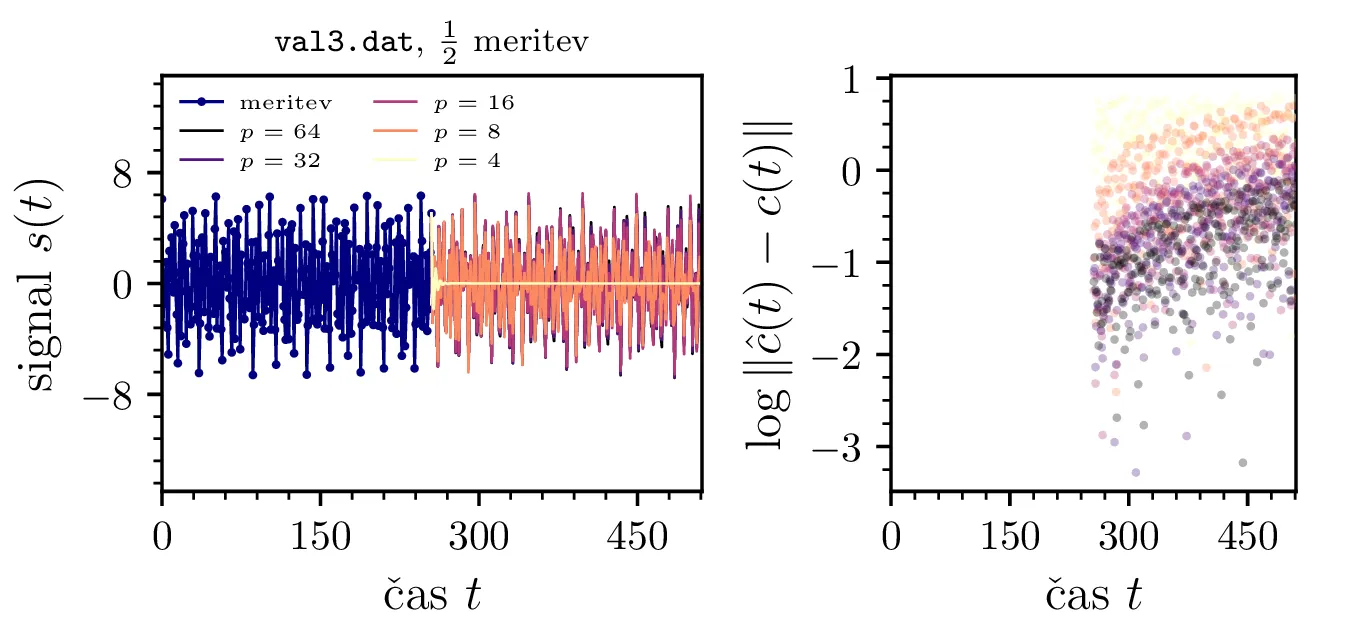
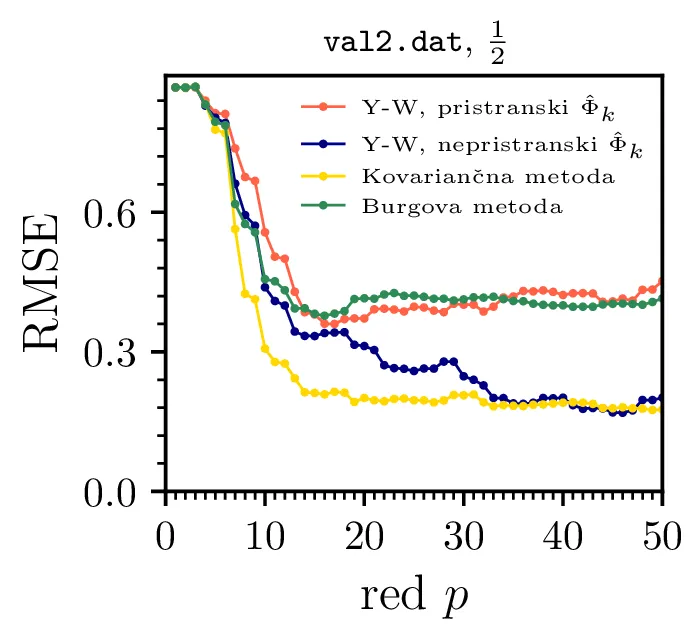
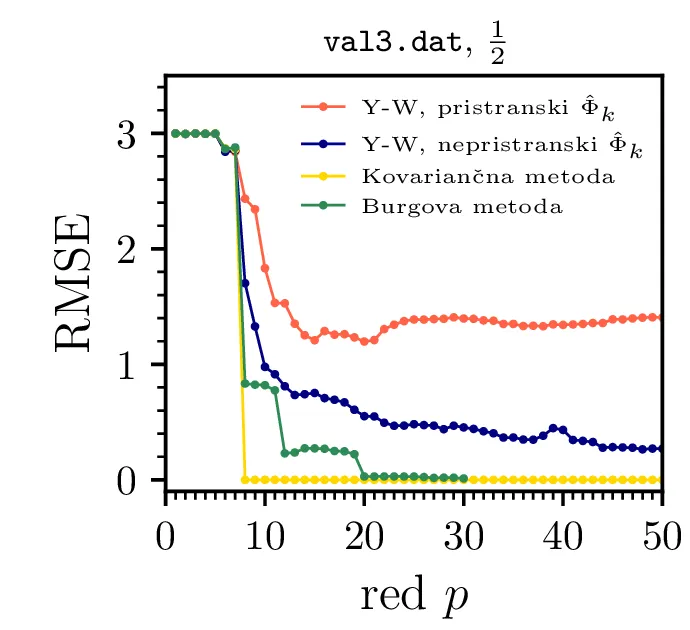
val2.dat in val3.dat. (Spodnja vrstica) Odvisnost RMSE odstopanja med napovedanim in
dejanskim signalom. RMSE izkazuje tipično obliko, kjer pri zadostnem redu napaka znatno pade, nato pa ostane
enaka ob zviševanju reda. Nekolikšna posebnost je signal val3.dat, kjer napaka pri napovedi z
kovariančno metodo (točneje arcovar) pade na 0. Preveril sem, da to ni artefakt, temveč da je
napoved dejansko točna, odstopanja so \(\sim10^{-8}\). Predvidevam, da je
signal val3.dat sintetično ustvarjen signal, na katerem slučajno kovariančna metoda ujame vso
relevantno dinamiko.
Vpliv deleža meritev in šuma
Na primeru signalov val2 in val3 si bomo še bolj podrobno pogledali še vpliv deleža
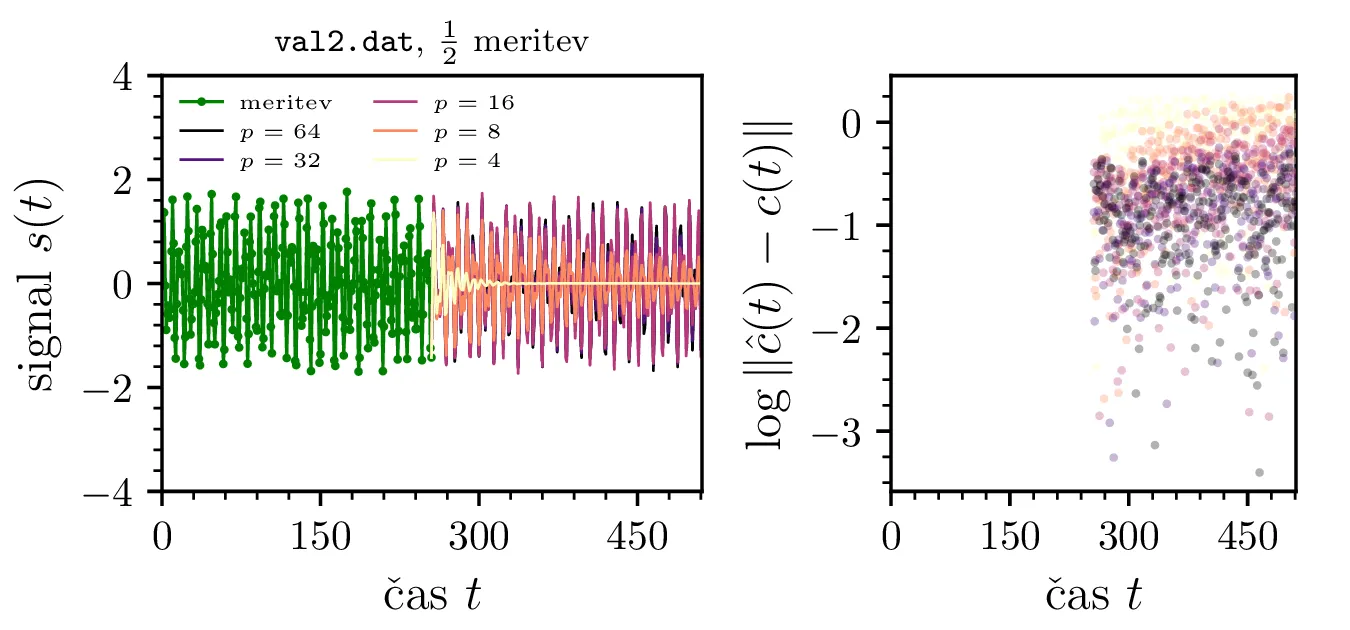
meritev za napoved in vpliv šuma. Napovedi iz prve polovice meritev vidimo na sliki 15
zgoraj. Velja omeniti še nekolikšno anomalijo, kjer je kovariančna metoda zmožna signal
val3.dat napovedati do strojne natančnosti. To me je presenetilo, a po preverbi, da so to zares
zgodi, sklepam, da je signal val3.dat nekakšen sintetičen signal, skonstruiran kot linearni filter
oblike 1.
Na sliki 16 je prikazan vpliv manjšanja deleža meritev na napoved, jasno je, da je potrebna neka minimalna količina meritev za določitev avtoregresijskih koeficientov, brez tega koeficientov ne moremo določiti in višanje reda avtoregresije je povsem nesmiseln overfitting. Vpliv dodanega šuma na napovedi obeh signalov je prikazan na sliki 17. Pri visokih \(p\), kjer so filtri skonvergirani, RMSE napaka napovedi približno linearno raste z amplitudo dodanega šuma.
Napoved za deklinacijo Lune
Na sliki 18 je prikazana napoved signala deklinacije lune iz \(1/2\) podatkov. Nekoliko zanimiva je odvisnost RMSE napake od reda avtoregresije, kjer kovariančna in Burgova metoda konvergirata mnogo hitreje, pri višjih \(p\) pa Yule-Walkerjeva metoda dejansko da nekoliko boljšo napoved.
Napoved Wolfovega števila
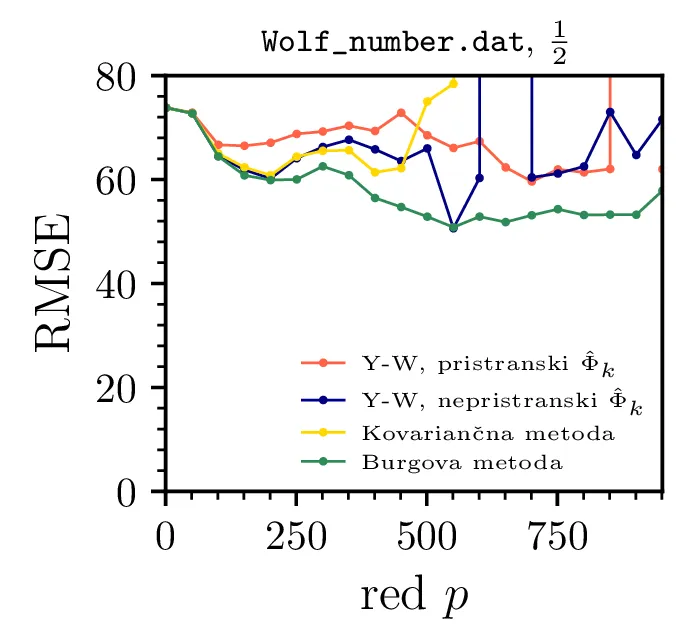
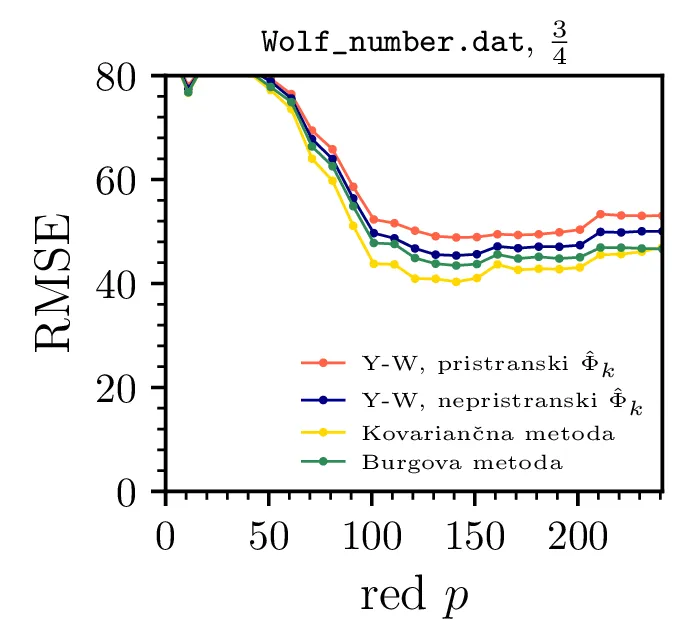
Na sliki 19 je prikazana napoved Wolfovega števila sončnih peg pri različnih deležih podatkov. Sprva se mi je zdelo, da je napoved Wolfovega števila povsem redundantno za nalogo, a izkazalo se je zanimivo v tem, da predstavlja primer procesa, ki je stacionaren na kratki skali, na daljši skali pa ne. Nestacionarnost na daljši skali vidimo, ko RMSE napaka sploh ne pade z višanjem reda, vse do \(p = 1000\) na sliki 19 sredinsko, kjer napovedujemo iz prve polovice meritev. Ko pa postanemo bolj skromni in napovedujemo le \(1/10\) celotnega obdobja meritev (na sliki 19 desno), postane proces dovolj stacionaren, da RMSE napaka napovedi pri \(p \approx 100\) znatno pade.
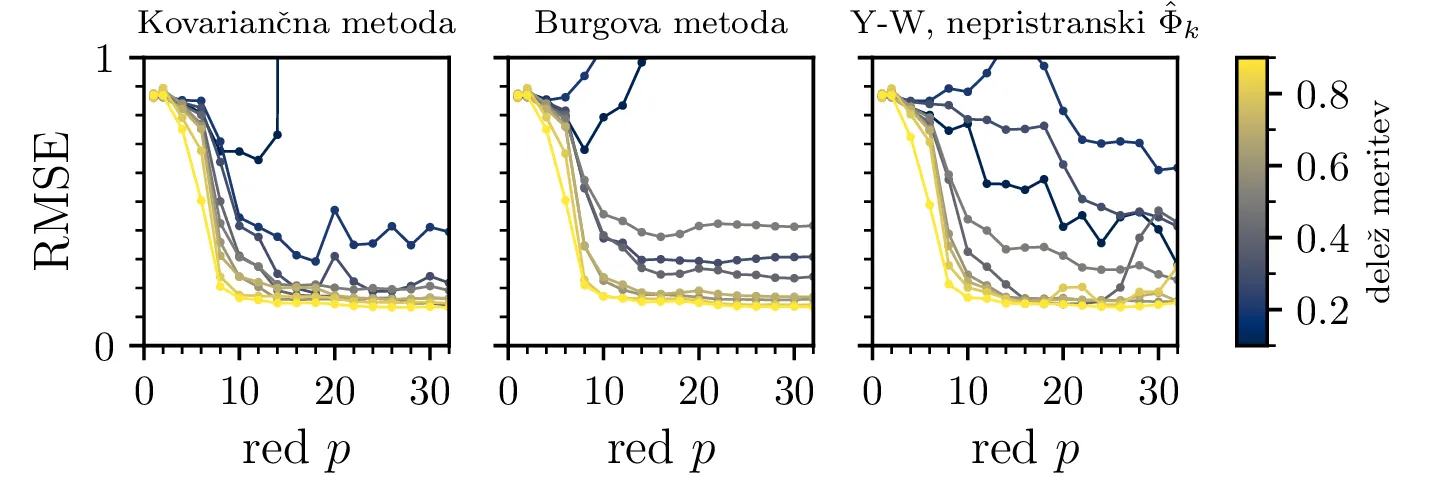
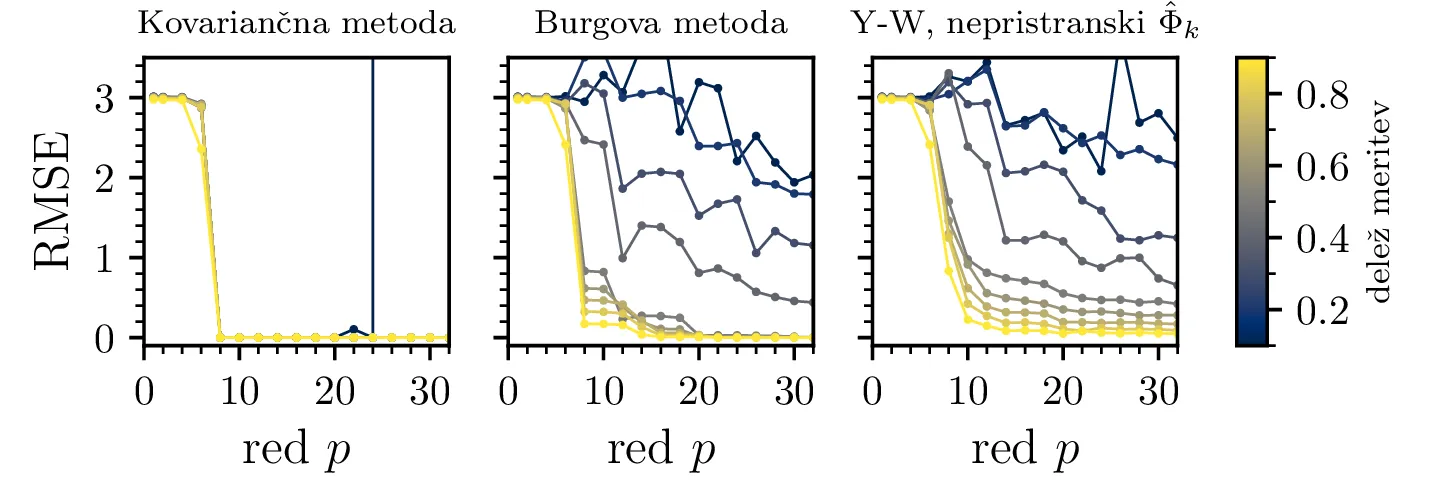
val2.dat (zgornja vrstica) oz. val3.dat (spodnja vrstica). RMSE pri velikih deležih
meritev, npr. 0.8, za oba signala in vse metode pade pri zadostnem redu
\(p\). Ko zmanjšujemo delež meritev, se trend prekine in dobimo napovedi, ki
z višanjem reda \(p\) ne postajajo bolj točne (RMSE z redom narašča). Zopet
je prisotna anomalija za signal val3 pri uporabi kovariančne metode, ki smo jo komentirali na
sliki 15.
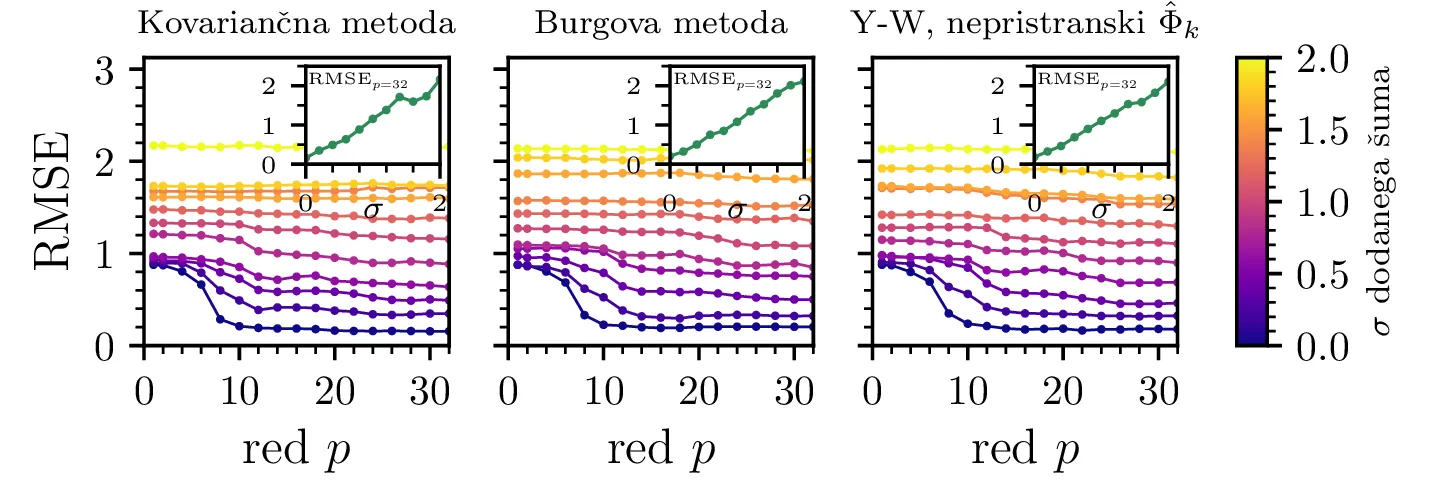
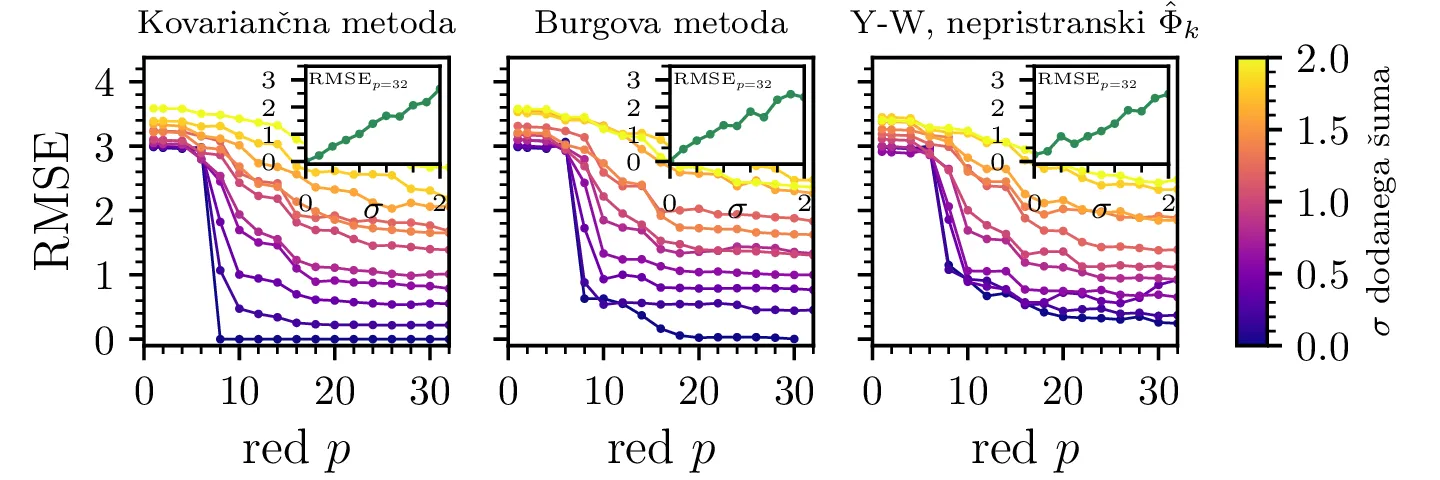
val2.dat (zgornja vrstica) oz. val3.dat (spodnja vrstica). Posebej za
signal val2 (zgornja slika) se jasno vidi, da pri dovolj močnem šumu napoved postane neuporabna
(ne opazimo več padca RMSE napake pri višanju reda). V manjših sličicah rišemo tudi naraščanje RMSE napake za
napovedi reda \(p = 32\), ki približno linearno narašča z amplitudo šuma
\(\sigma\).
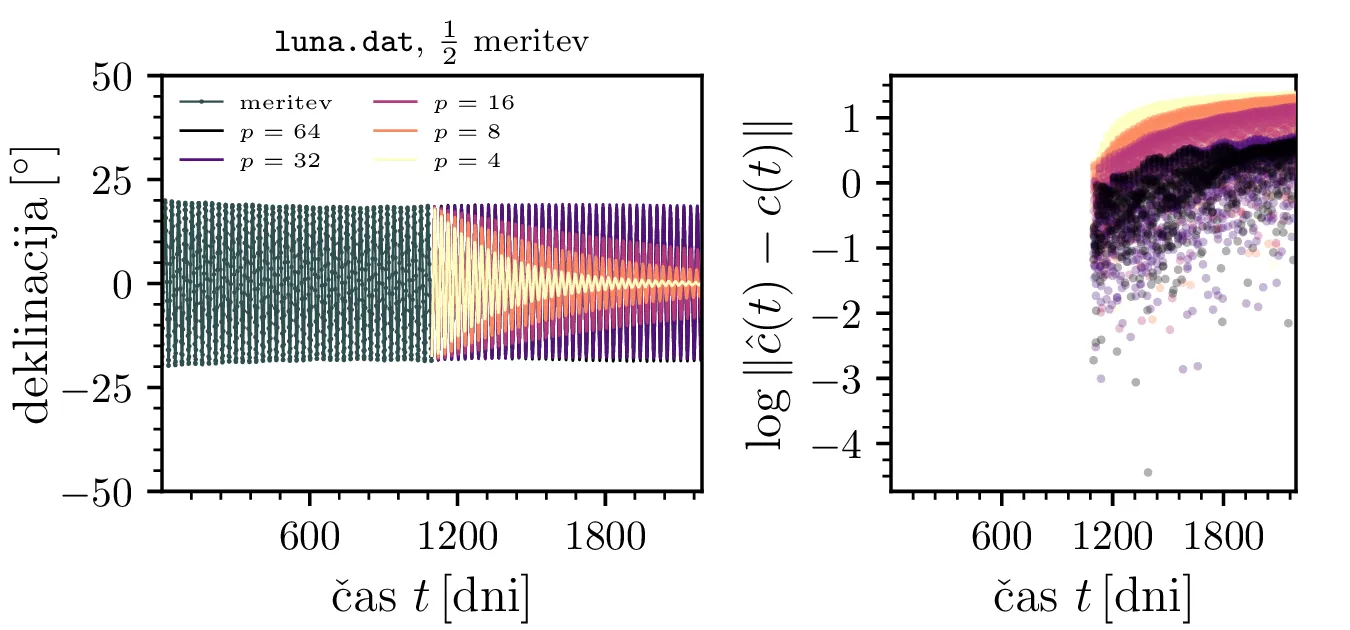
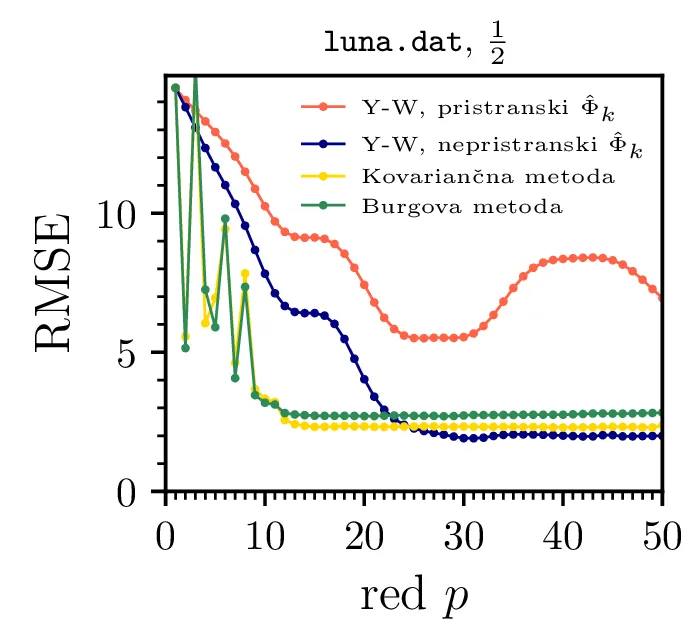
luna.dat. (Levo in sredinsko) Napovedi in odstopanja za različne rede avtoregresije. (Skrajno
desno) RMSE odstopanje druge polovice pravega signala od napovedih vrednosti. Vidimo, da Burgova in
kovariančna metoda najhitreje konvergirata k neki relativno nizki napaki, pri
\(p > 25\) pa je Yule-Walker metoda z nepristransko oceno avtoregresije
celo nekoliko boljša.
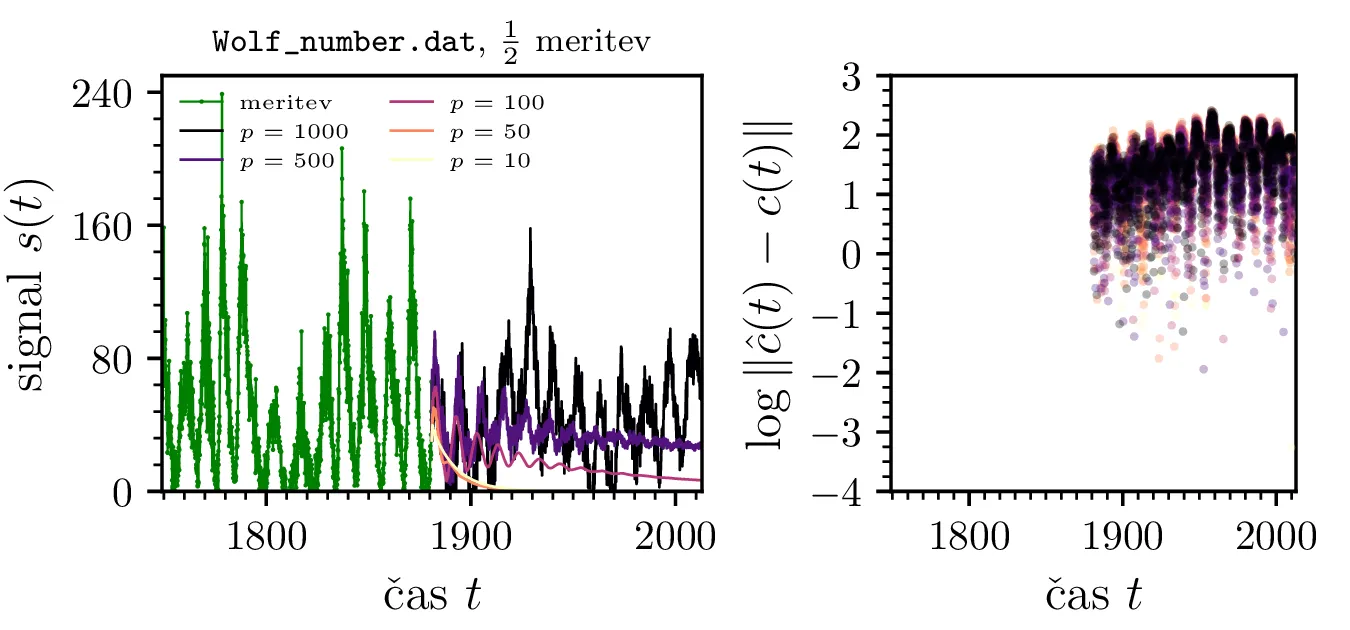
Wolf_number.dat. (Levo) Napovedi za različne rede avtoregresije. Tu se poslužujemo mnogo višjih
redov avtoregresije, saj nižji redi, ki smo jih uporabljali npr. na koncentraciji
\(\mathrm{CO}_2\), dajo napovedi, ki so že vizualno povsem napačne (glej npr.
napoved reda \(p = 100\) v vijolični barvi). Pri tako velikih redih je
matrika Yule-Walkerjeve metode ill-conditioned in sistem je numerično nestabilen, kot smo opazili že
na slikah 7
in 9 v srednji vrstici.
Zato namesto Yule-Walker uporabljamo Burgovo metodo za oceno avtoregresijskih koeficientov. (Sredinsko in
desno) RMSE odstopanje pravega signala od napovedih vrednosti. Napoved iz prve polovice podatkov je neuspešna,
niti pri \(p = 1000\) ne dosežemo znatnega padca v odstopanju. Situacija je
boljša za napoved iz prvih \(3/4\) meritev, kjer RMSE napaka znatno pade za
\(p > 100\). Vidimo torej, da je lahko proces na krajših časovnih skalah
stacionaren, na daljših pa ne.
Napoved borze, naloga za tepce
Na sliki 20
je prikazana napoved borznega signala in pripadajoče napake. O napovedih borze bi lahko diskutirali poljubno
dolgo, saj je problem izjemno močno motiviran. A če je bila neka smiselna napoved možna za signale
\(\mathrm{CO}_2\) koncentracij, za signala val2 in
val3, za Lunino deklinacijo in celo za število sončnih peg, je borza nekoliko drugačna zver.
Napoved sicer ujame splošni trend rasti borze, a dejanskega gibanja cen niti približno ne zadane. To je namreč
podvrženo najbolj kaotični izmed naravnih sil – človeškemu razumu in neumnosti. Če bi namreč ceno bilo mogoče
napovedati, bi oseba z dostopom do te informacije sodelovala v kupovanju oz. prodajanju, na način, da bi
premagala trg (ang. beating the market). Takšna oseba bi morda za kratek čas nesramno obogatela, a v
modernem svetu se informacije širijo hitro, in še tako sofisticirana statistična metoda je kmalu dostopna vsem.
Tedaj je ta informacija dostopna vsem in je na vsaki točki v času že vključena v trenutno ceno.
Glede na to, da so avtoregresijski modeli oz. splošneje ARMA modeli znani že vsaj od 1970, so dostopni vsakomur, ki ima dovolj matematičnega znanja in željo po hitrem zaslužku. Zato bi težko pričakovali, da taka informacija še ni vključena v ceno. Naša napoved je torej bolj ali manj oslovska, po principu garbage-in, garbage-out. Borza namreč niti v prvem približku ni stacionaren linearni proces, temveč nekaj mnogo manj oprijemljivega.
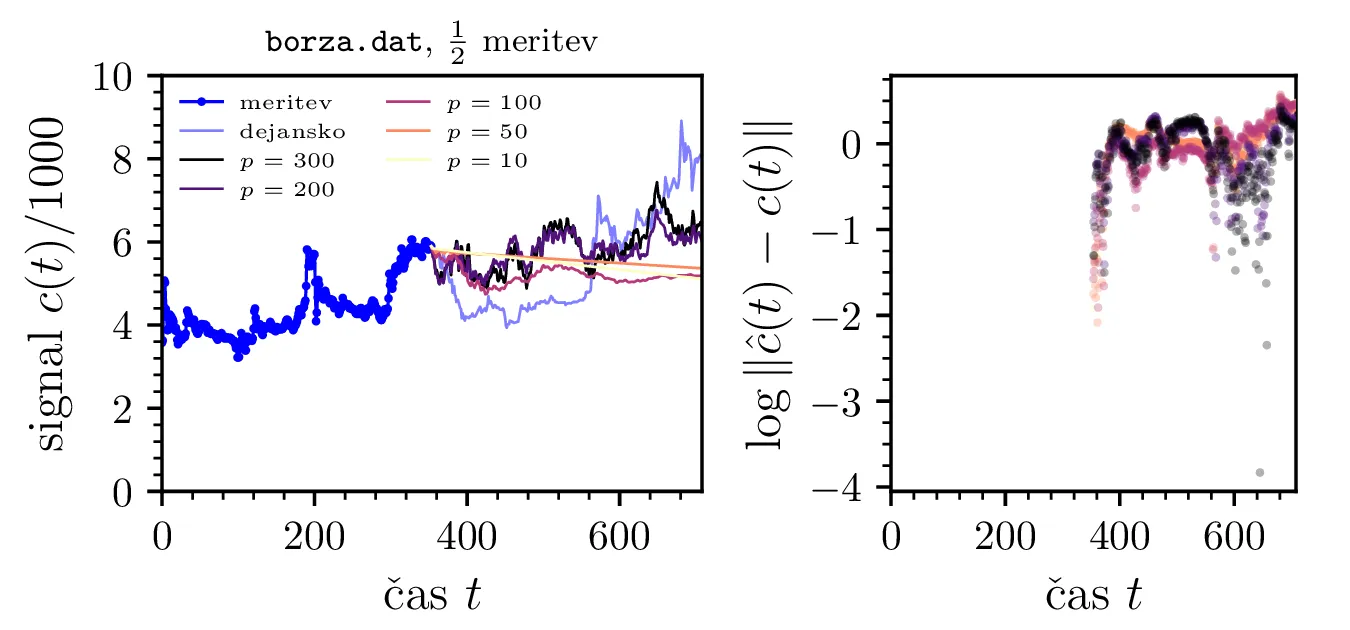
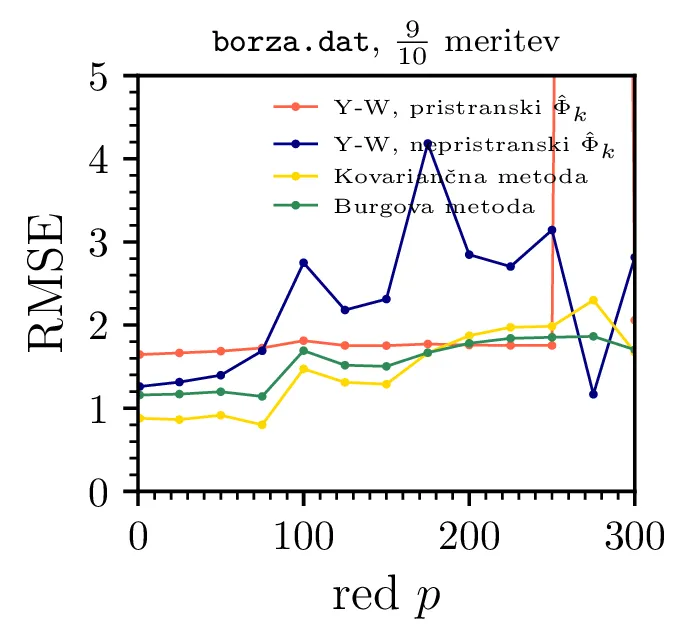
borza.dat. Zadeli smo trend navzgor, a nekako
pričakovano je, da so napovedi fluktuacij bolj slabe – v nasprotnem primeru bi bili vsi študentje fizike
nesramno bogati (ali bolj učeno, trg je vsaj do neke mere učinkovit). Tudi če smatramo le napoved zadnje
desetino pravega signala, ne dosežemo nikakršnega zmanjšanja v RMSE (slika skrajno desno).