Modelska analiza I
11. naloga: Optimalno filtriranje
Navodila
Kadar z zaporednimi meritvami spremljamo časovni razvoj procesa, katerega dinamiko poznamo, lahko s filtriranjem dosežemo občutno boljšo natančnost, kot jo dajejo surove meritve. Kalmanov filter deluje na principu optimalnega uteževanja linearne napovedi stanja ter novih meritev, kar doseže s sprotnim vodenjem evidence o kovarianci trenutne ocene stanja.
Naj bo \(\mathbf{x}_n\) vektor stanja sistema ob času \(n\), \(P_n\) pa pripadajoča kovariančna matrika, ki opisuje njegovo statistično negotovost. Potrebujemo še začetno stanje \(\mathbf{x}_0^+\) ter kovarianco \(P_0^+\), ki ju običajno dobimo iz prve surove meritve. Komponentam stanja, ki niso na voljo, nastavimo velike začetne kovariance.
Kalmanov filter poteka v dveh korakih. Prvi korak je izvedba časovnega koraka na trenutni napovedi stanja. Fizikalni sistem naj uboga časovno evolucijo \begin{equation}\mathbf{x}_{n+1} = F_n \mathbf{x}_n + \mathbf{c}_n + \mathbf{w}_n, \label{eq:process}\end{equation} kjer je \(F_n\) prehodna matrika sistema, \(\mathbf{c}_n\) kontrolni vektor, \(\mathbf{w}_n\) pa vektor Gaussovega šuma s povprečjem \(0\) in kovariančno matriko \(Q_n\). Napovemo novo stanje \(\mathbf{x}^-_{n+1}\) ter njegovo kovariančno matriko \(P^-_{n+1}\): \[\begin{aligned} \mathbf{x}^-_{n} &= F_n \mathbf{x}^+_{n-1} + \mathbf{c}_{n}, \\ P^-_{n} &= F_{n} P^+_{n-1} F^T_{n} + Q_{n}. \end{aligned}\] Sledi izboljšava te napovedi z novimi meritvami. V splošnem ne merimo neposredno komponent vektorja stanja \(\mathbf{x}_n\), temveč neko linearno kombinacijo \[\mathbf{z}_n = H_n \mathbf{x}_n + \mathbf{r}_n,\] kjer je \(H_n\) matrika, ki določa, kaj merimo, \(\mathbf{r}_n\) pa šum meritve s kovariančno matriko \(R_n\). Matrika \(H_n\) je lahko singularna, če merimo manj spremenljivk, kot je dimenzija sistema. Posodobitev poteka po enačbah: \begin{equation}\begin{aligned} \mathbf{x}^+_{n} &= \mathbf{x}^-_{n} + K_{n} \left( \mathbf{z}_{n} - H_{n} \mathbf{x}^-_{n} \right), \\ P^+_{n} &= \left( I - K_{n} H_{n} \right) P^-_{n}, \label{eq:correction} \end{aligned}\end{equation} pri čemer je \(K_{n+1}\) faktor ojačanja, ki določa, s kolikšno utežjo nova meritev prispeva k popravku. \[K_{n} = P^-_{n} H^T_{n} \left( H_{n} P^-_{n} H^T_{n} + R_{n} \right)^{-1}.\]
Rešitev
Začeli bomo s povsem tipičnim načinom uporabe Kalmanovega filtra, sicer na primeru vožnje avtomobila. Za gibanje vozila moramo zapisati časovno evolucijo v obliki 1, pri čemer je vektor stanja \[\mathbf{x} = \left( x, y, v_x, v_y \right).\] Preprost model gibanja brez zunanjih sil opiše prvi člen \(\mathbf{x}_{n+1} = F_n \mathbf{x}_n\), pri čemer je prehodna matrika \[F_n = \begin{pmatrix} I_{2\times 2} & I_{2\times 2} \Delta t \\ 0 & I_{2\times 2} \end{pmatrix}.\] Če imamo prisotne zunanje sile, jih upoštevamo preko kontrolnega vektorja in šuma, tako da je časovna evolucija \begin{equation}\mathbf{x}_{n+1} = F \mathbf{x}_n + G \mathbf{a}_n + G \mathbf{\xi}_n = F_n \mathbf{x}_n + \begin{pmatrix} \Delta t^2 / 2 & 0 \\ 0 & \Delta t^2 / 2 \\ \Delta t & 0 \\ 0 & \Delta t \\ \end{pmatrix} \begin{pmatrix} a_x \\ a_y \end{pmatrix} + \begin{pmatrix} \Delta t^2 / 2 & 0 \\ 0 & \Delta t^2 / 2 \\ \Delta t & 0 \\ 0 & \Delta t \\ \end{pmatrix} \begin{pmatrix} \xi_x \\ \xi_y \end{pmatrix}, \label{eq:constant-a-model}\end{equation} pri čemer je drugi člen kontrolni vektor, ki ga lahko vsaj v principu točno poznamo, tretji člen pa vpliv zunanjega okolja, ki ga ne moremo opisati s preprostim modelom. Te sile modeliramo z Gaussovskim šumom \(\mathbf{\xi}_n \sim \mathcal{N}(0, \Sigma_a)\), pri čemer je kovariančna matrika \(\Sigma_a = \sigma_a^2 I_{2\times 2}\). Poznamo torej procesni šum, člen \(G \mathbf{\xi}_n\), iz česar lahko določimo njegovo kovariančno matriko \(Q_n = \mathop{\mathrm{Cov}} \left[ \mathbf{w}_n \right]\) \begin{equation}Q_n = \mathop{\mathrm{Cov}} \left[ G \mathbf{\xi}_n \right] = G G^T \sigma_a^2 = \begin{pmatrix} \frac{\Delta t^4}{4} & 0 & \frac{\Delta t^3}{2} & 0 \\ 0 & \frac{\Delta t^4}{4} & 0 & \frac{\Delta t^3}{2} \\ \frac{\Delta t^3}{2} & 0 & \Delta t^2 & 0 \\ 0 & \frac{\Delta t^3}{2} & 0 & \Delta t^2 \end{pmatrix}. \label{eq:constant-a-model-Q}\end{equation}
V navodilih naloge1 je predlagan še preprostejši model, kjer zanemarimo pospešenost gibanja znotraj enega \(\Delta t\). Tedaj se časovna evolucija poenostavi, sicer se spremeni kontrolna matrika \[\begin{aligned} G: \begin{pmatrix} \Delta t^2 / 2 & 0 \\ 0 & \Delta t^2 / 2 \\ \Delta t & 0 \\ 0 & \Delta t \\ \end{pmatrix} \mapsto \begin{pmatrix} 0 & 0 \\ 0 & 0 \\ \Delta t & 0 \\ 0 & \Delta t \\ \end{pmatrix}, \quad\text{Poenostavitev, nepospešeno gibanje}, \end{aligned}\] kovariančna matrika procesnega šuma pa postane diagonalna \[\begin{aligned} Q_n: \begin{pmatrix} \frac{\Delta t^4}{4} & 0 & \frac{\Delta t^3}{2} & 0 \\ 0 & \frac{\Delta t^4}{4} & 0 & \frac{\Delta t^3}{2} \\ \frac{\Delta t^3}{2} & 0 & \Delta t^2 & 0 \\ 0 & \frac{\Delta t^3}{2} & 0 & \Delta t^2 \end{pmatrix} \mapsto \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & \Delta t^2 & 0 \\ 0 & 0 & 0 & \Delta t^2 \end{pmatrix}, \quad\text{Poenostavitev, nepospešeno gibanje}. \end{aligned}\]
Vrednotenje napovedi
Zdaj lahko ta dva modela uporabimo za filtriranje trajektorij vozila, ki preko GPS dobiva podatke o poziciji,
hkrati pa meri svojo hitrost in pospešek (zaenkrat v laboratorijskem sistemu). Tako filtrirane oz. napovedane
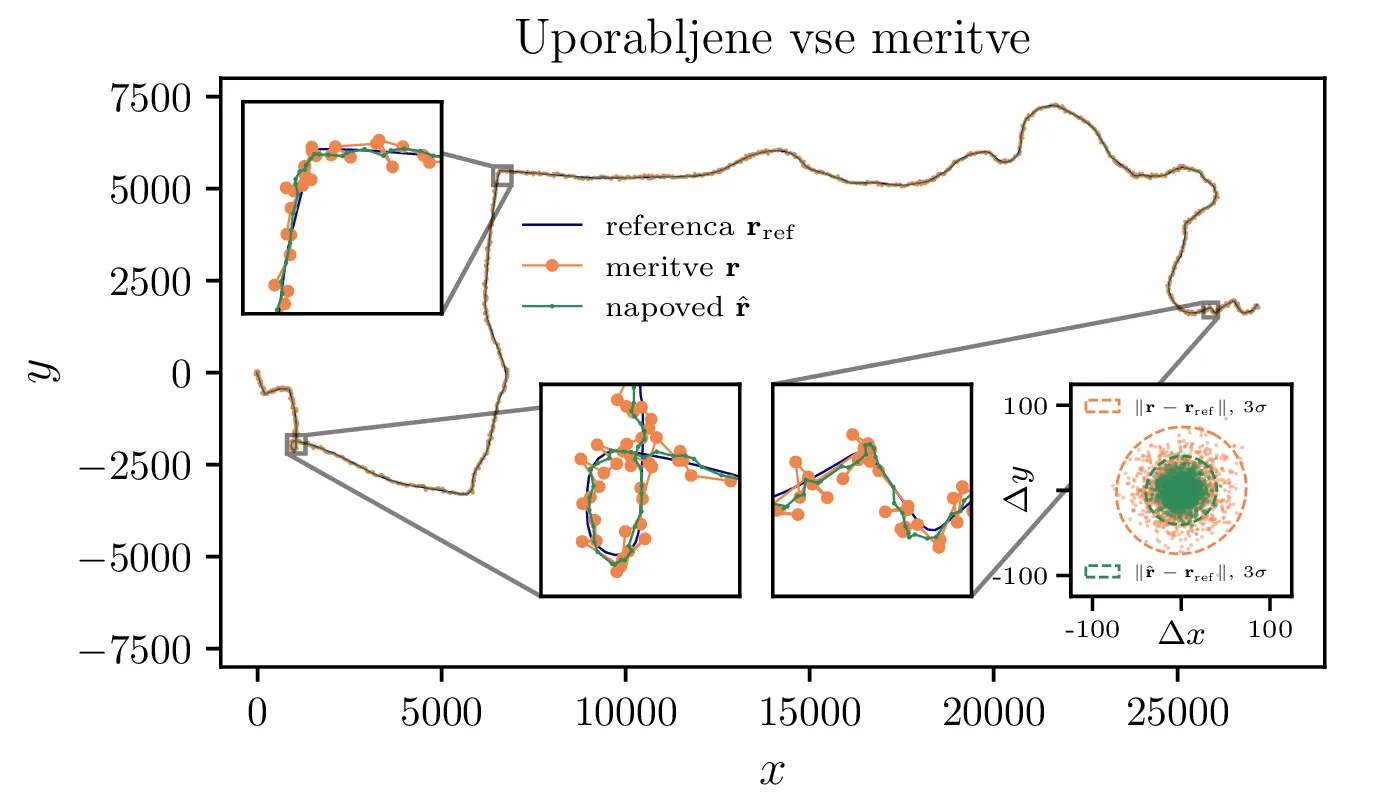
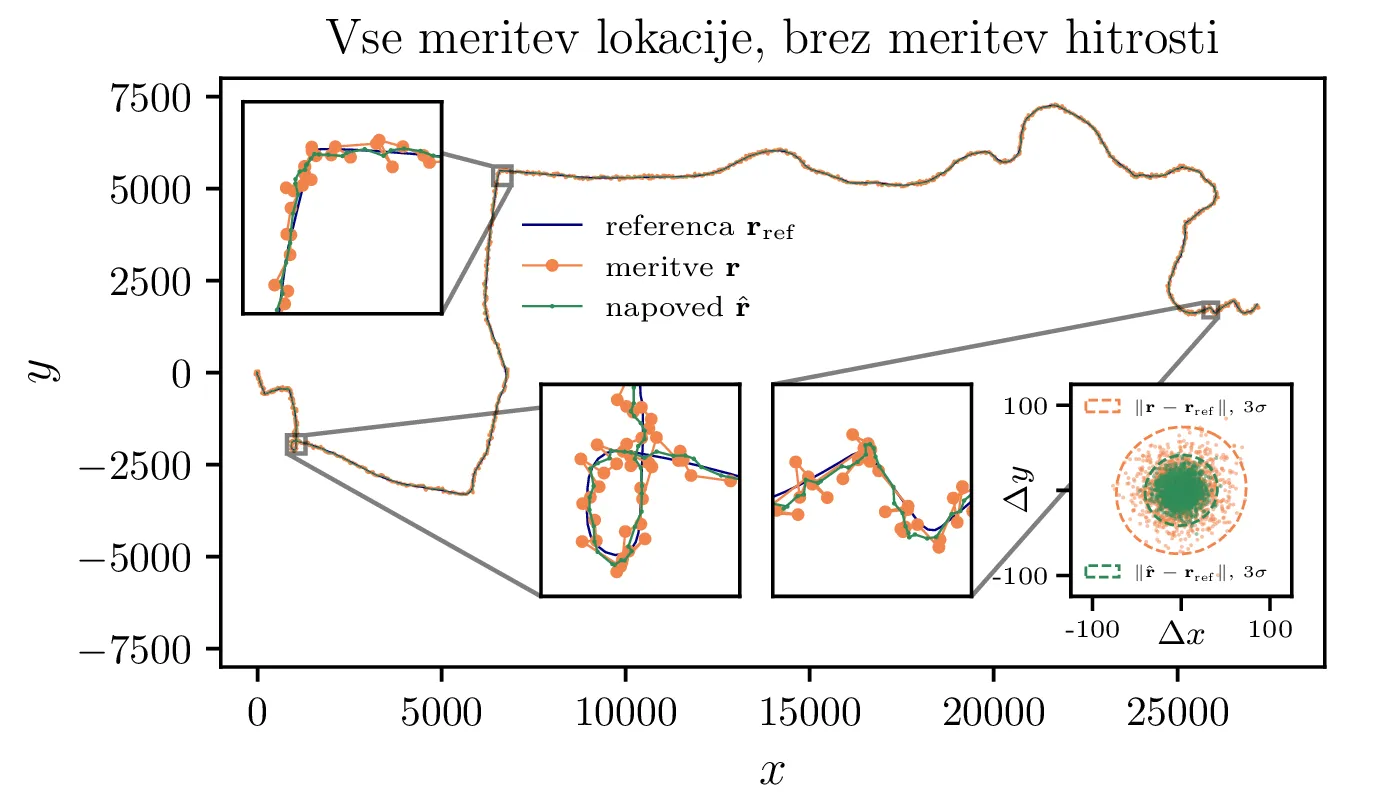
trajektorije vidimo na sliki 1, kjer uporabimo vseh 1400 razpoložljivih meritev \(x, y\) in
\(\mathbf{v}\) iz datoteke kalman_cartesian_data.dat.
Napovedi, ki jih izračunamo s Kalmanovim filtrom, vrednotimo s primerjavo z referenčnimi podatki o pozicijah
\(\mathbf{r}_\mathrm{ref}\) in hitrostih
\(\mathbf{v}_\mathrm{ref}\) iz datoteke
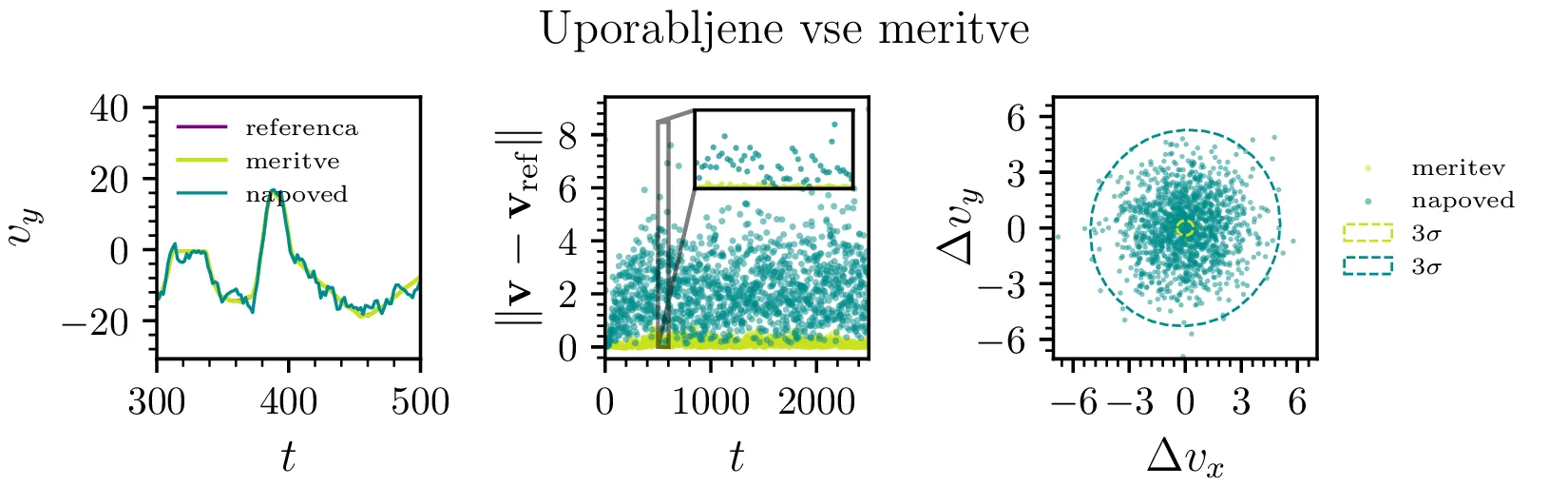
kalman_cartesian_control.dat. Na histogramu na sliki 1
vidimo, kako so napovedi porazdeljene tesneje kot meritve, okoli referenčne trajektorije
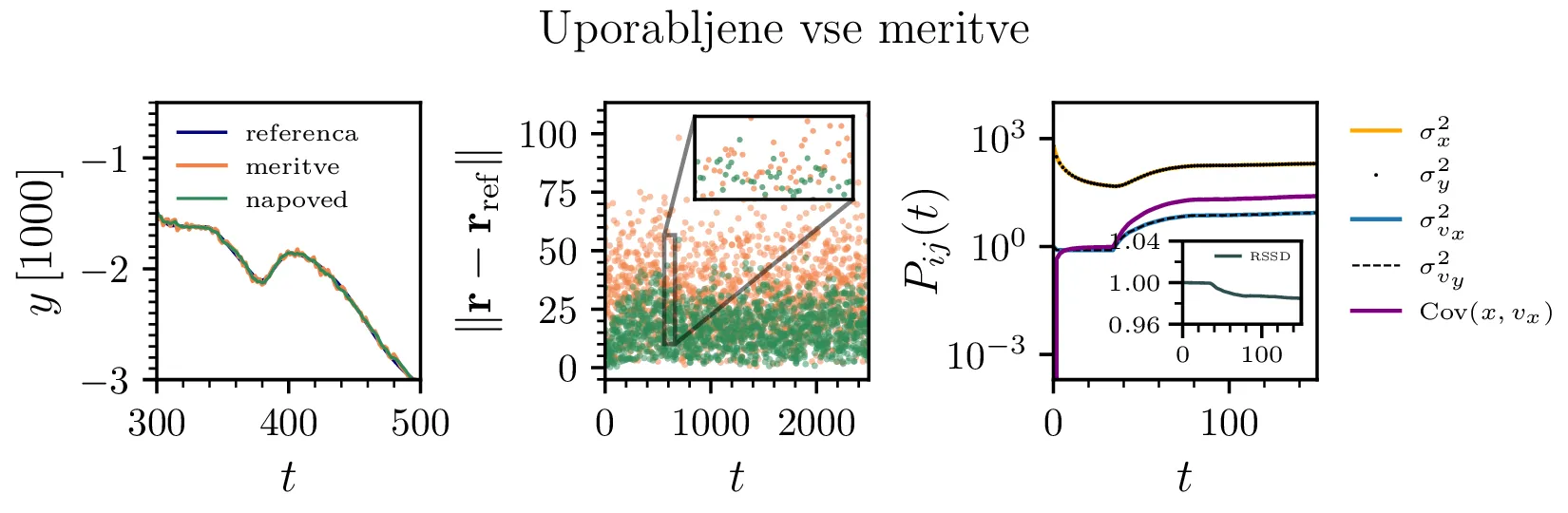
\(\mathbf{r}_\mathrm{ref}(t)\). Na sliki 2
vidimo tudi časovno dinamiko tega odstopanja in časovno dinamiko kovariančne matrike
\(P\), kjer je razviden kratek prehod, po katerem se elementi
\(P\) ustalijo pri nekih stacionarnih vrednostih.
Izpuščanje meritev
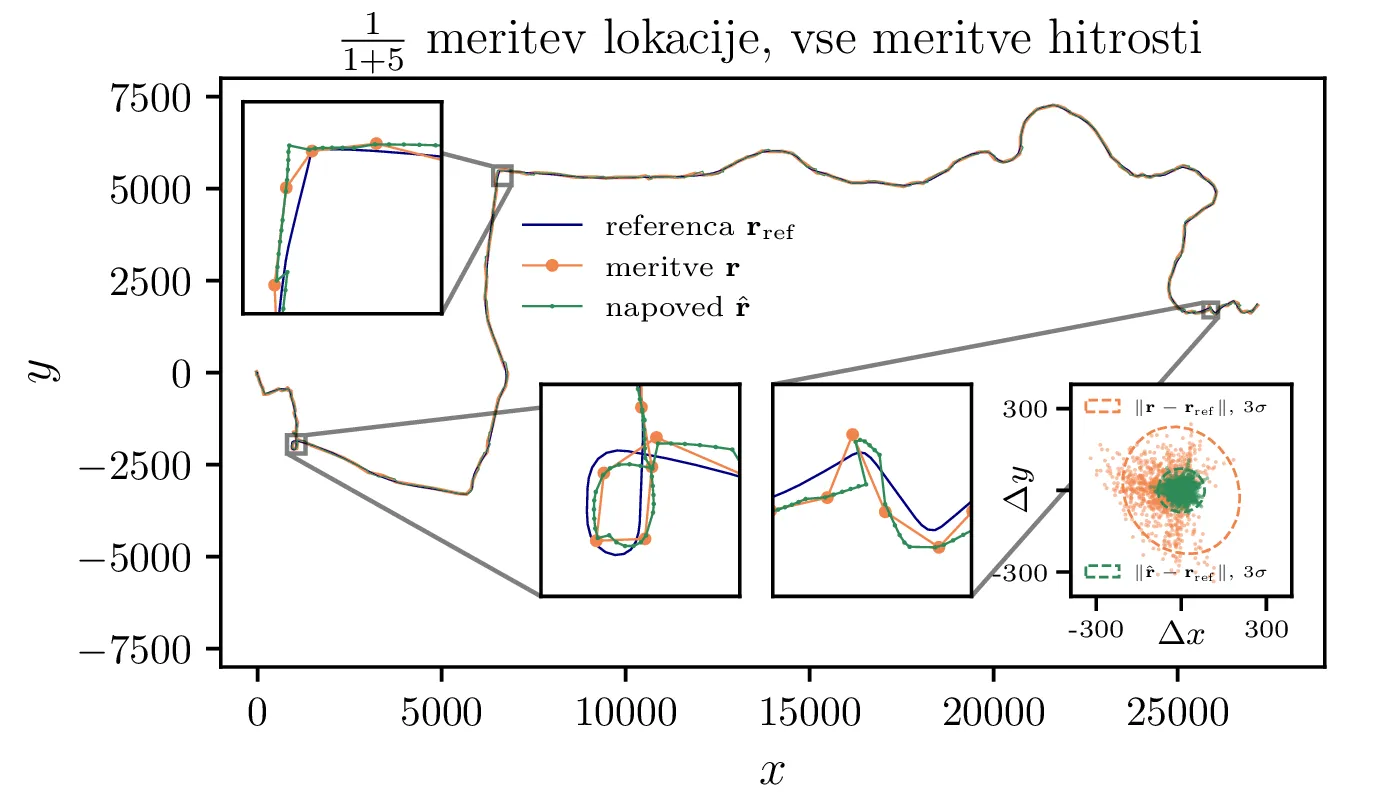
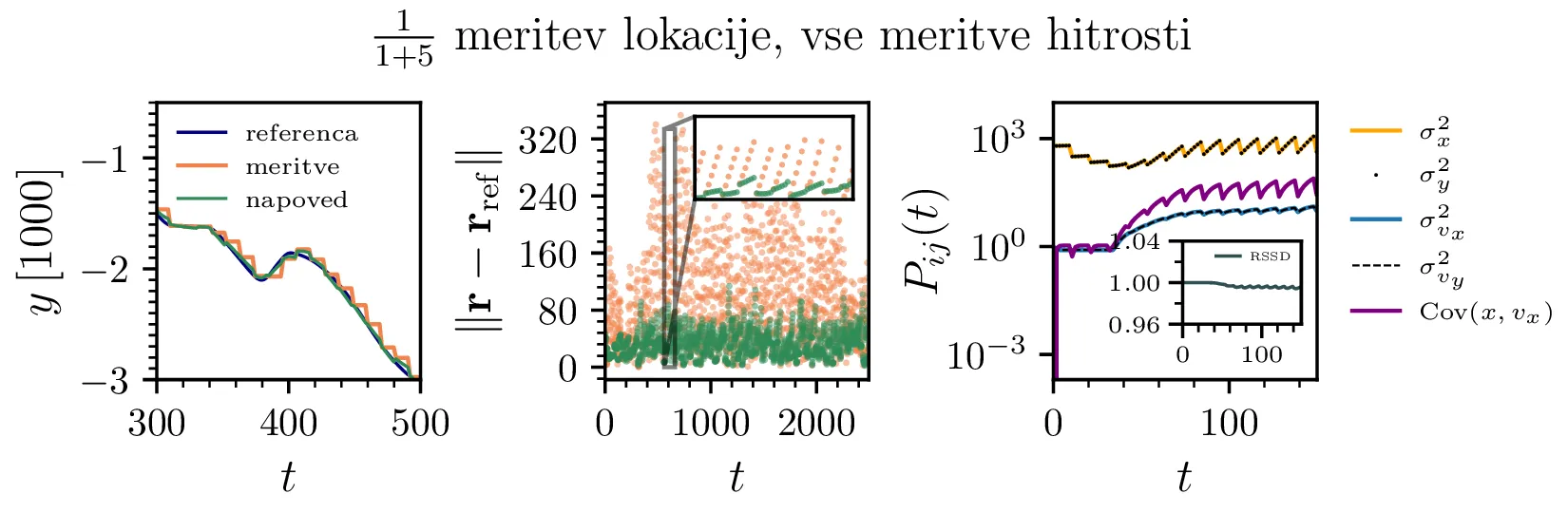
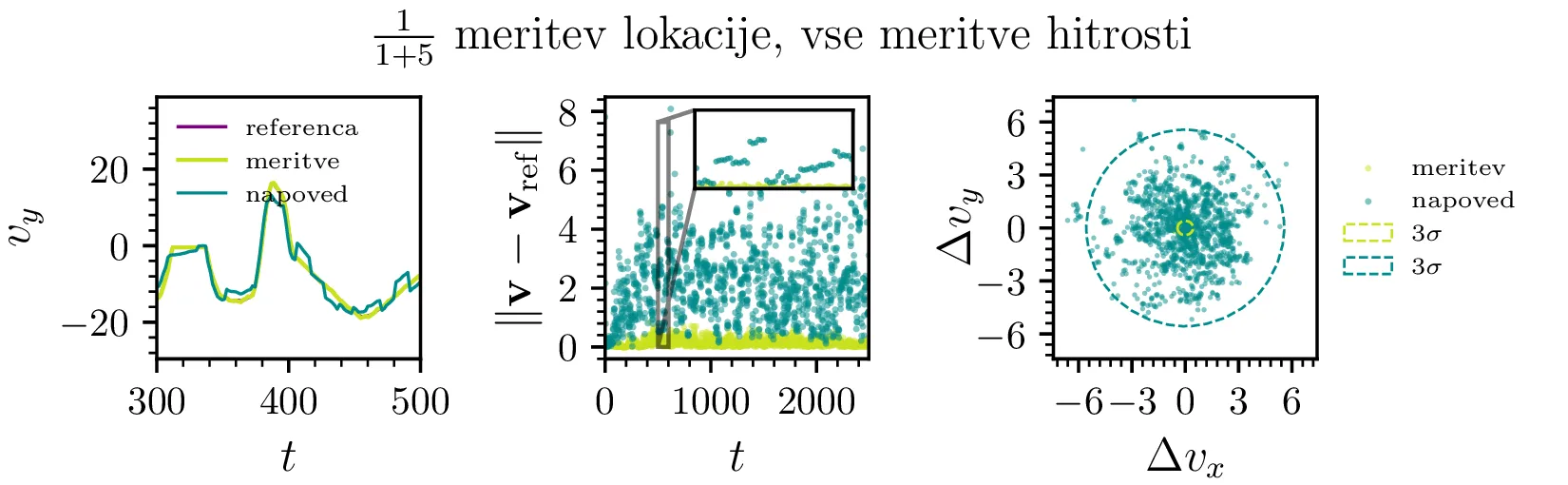
Naš vektor stanja \(\mathbf{x} = \left( x, y, v_x, v_y \right)\) vključuje tako pozicijo kot hitrost. Vsako izmed teh količin (pozicija in hitrost) merimo z popolnoma drugim senzorjem. Tipično je, da hitrost zajema ni enaka za ta dva senzorja. Na primer, če je zajem hitrosti hitrejši od GPS signala, imamo na vsako meritev \([\mathbf{r}, \mathbf{v}]\) imamo na voljo še \(5\) meritev le hitrosti \(\mathbf{v}\). Tak scenarij, kjer le \(\frac{1}{1+5}\) meritev vključuje pozicijo, vidimo na sliki 3. Vidimo, da to povzroči periodično rast odstopanja, kar je razvidno iz odsečne oblike trajektorije, pa tudi iz odstopanje na sliki 3 spodaj sredinsko in periodične dinamike varianc na isti sliki desno spodaj.
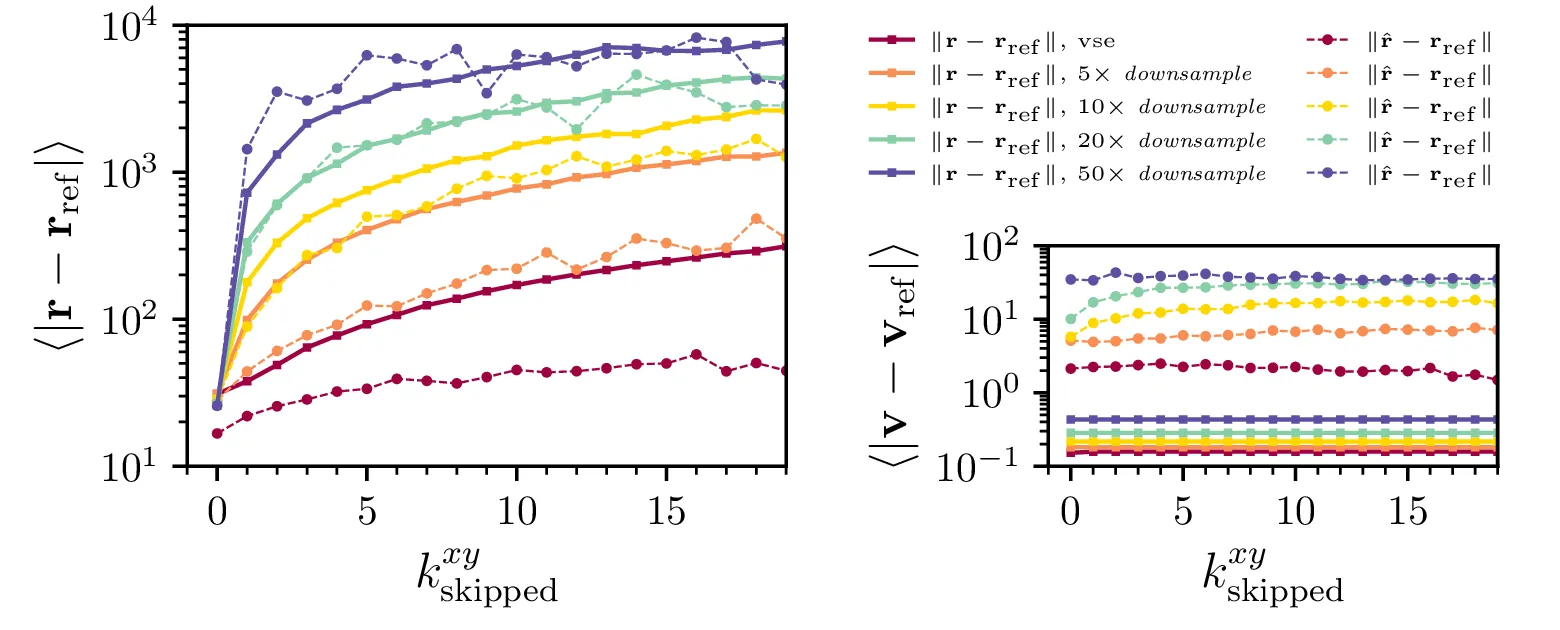
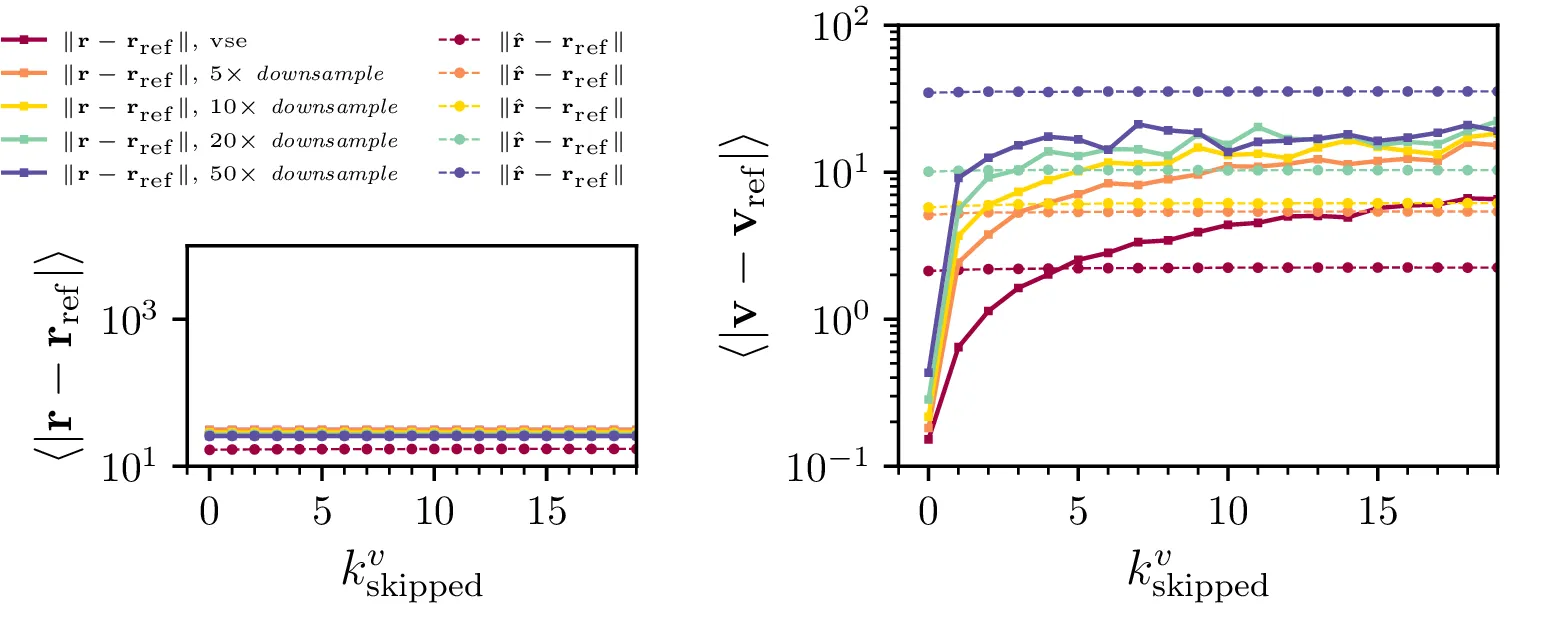
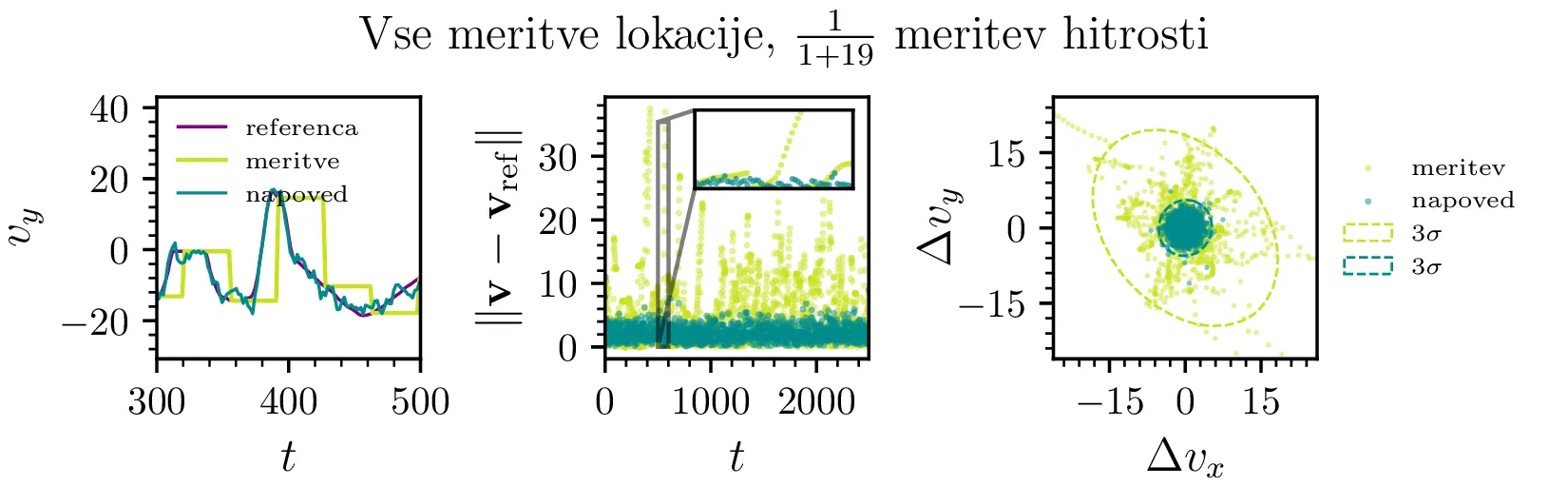
Bolj sistematično lahko učinek izpuščanja meritev pogledamo za splošno število izpuščenih meritev. Torej tako, da meritve z pozicijo predstavljajo le \(\frac{1}{1 + k_\mathrm{skipped}^{xy}}\) vseh meritev. Na sliki 4 pričakovano vidimo, da z izpuščanjem meritev odstopanje napovedi raste, rast pa je počasnejša meritve, ki so v splošnem bolj goste. Pomembna je opazka iz slike 4 desno, t. j.dejstvo, da izpuščanje meritev pozicije le minimalno vpliva na odstopanje v hitrostnem delu napovedi, torej na \(\| \hat{\mathbf{v}} - \mathbf{v}_\mathrm{ref} \|\). Nekoliko presenetljiv je nasprotni scenarij na sliki 5, kjer namesto pozicij izpuščamo meritve hitrosti, to pa ne vpliva niti na odstopanje napovedanih pozicij niti na odstopanje napovedanih hitrosti.
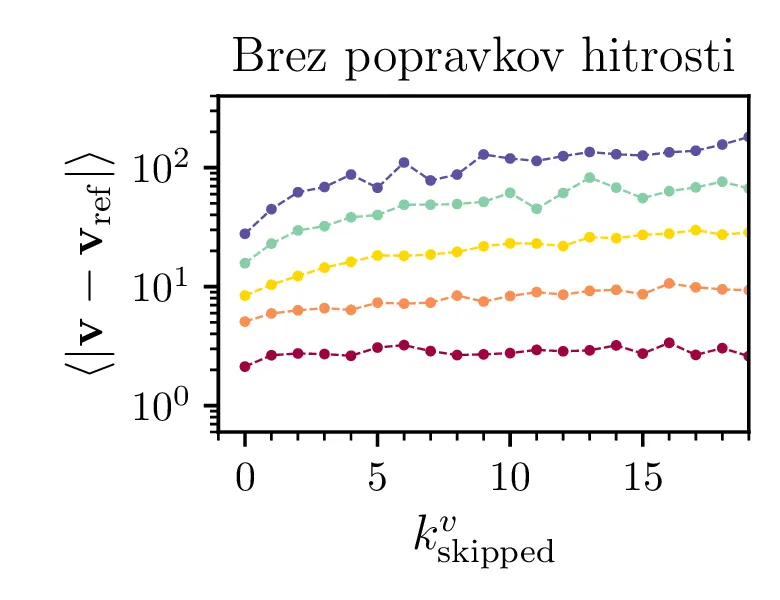
Pri gostih meritvah pozicij je torej Kalmanov filter zmožen zapolniti manjkajoče meritve hitrosti, preko ocene \(\hat{\mathbf{v}}_i = (\mathbf{r}_{i} - \mathbf{r}_{i-1}) / \Delta t\), ki pa je implicitna v samem delovanju Kalmanovega filtra. Zares se gre za popravke v obliki \begin{equation}v^+_n = v^-_n + K_{v, x} (z_x - x^-_{n}), \label{eq:position-to-velocity-corrections}\end{equation} kjer se inovacija v meritvi položaja prenese v novo napoved za hitrost. Da tak popravek zares zagotovi točnost napovedi, lahko vidimo na sliki 6, kjer umetno nastavimo \(2\times 2\) blok \(K_{\mathbf{v}, \mathbf{x}}\) na \(0\), ob čemer opazimo naraščanje napake za napoved hitrosti. Pričakovali bi lahko, da bi filter podobno nadomestil manjkajoče meritve pozicije, a ker pozicijo dobimo iz hitrosti z integracijo, se napake akumulirajo. Ob gostih meritvah hitrosti torej izpuščanje meritev pozicije vodi do precejšnjih odstopanj (slike 4), pri gostih meritvah pozicije pa lahko izpuščene meritve hitrosti v celoti nadomestimo (slika 5). Dodatna potrditev za to, da lahko natančne napovedi hitrosti dosežemo ali z gostimi meritvami hitrosti ali z gostimi meritvami pozicije, vidimo na sliki 8, kjer je napaka napovedi hitrosti zelo primerljiva za drugo vrstico, kjer imamo redke lokacije in goste hitrosti, in tretjo vrstico, kjer imamo goste lokacije in redke hitrosti.
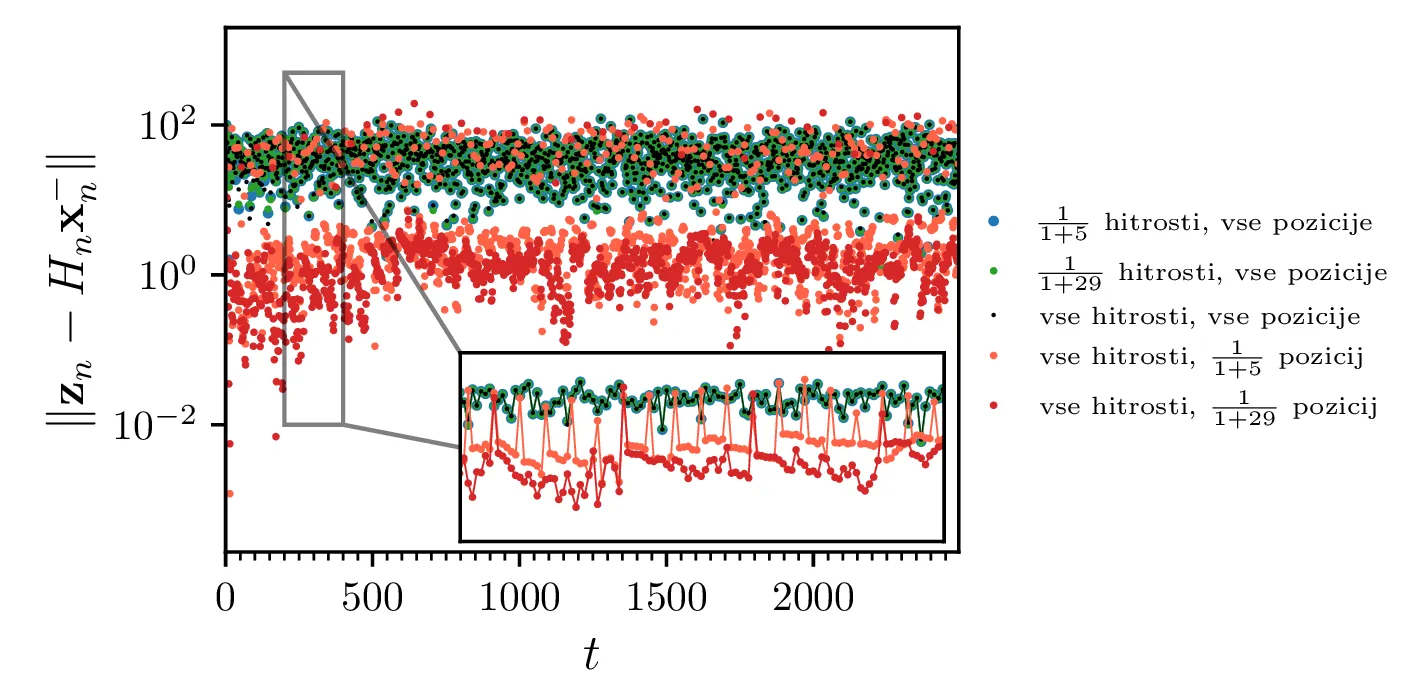
Pomemben vpogled v obnašanje Kalmanovega filtra je tudi dinamika popravkov \(\mathbf{z}_n - H_n \mathbf{x}_n^-\), ki jo vidimo na sliki 7. Za izpuščene meritve pozicij jasno opazimo, da so prisotni večji popravki, sovpadajoči s periodo izpuščenih meritev.
Tunel
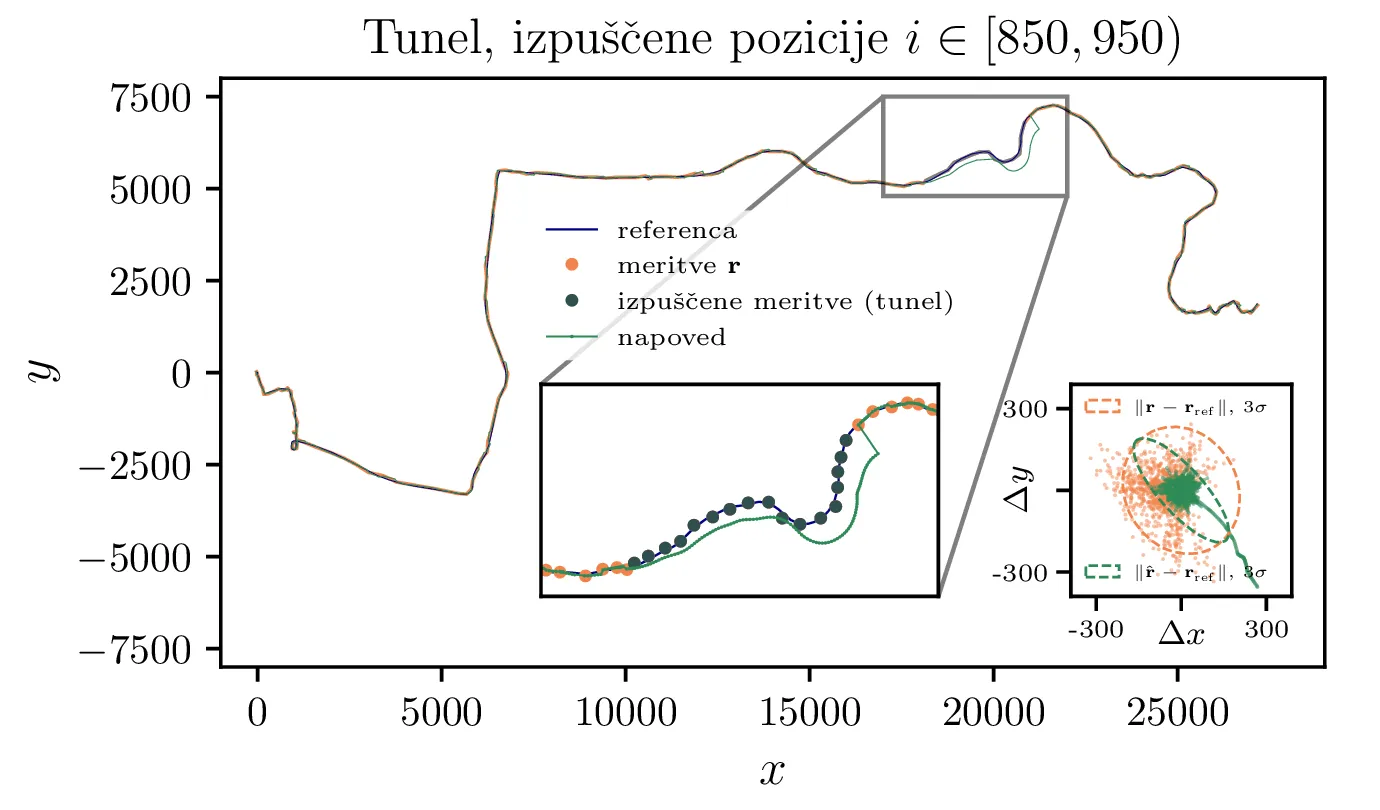
Zanimivo je pogledati tudi obnašanje Kalmanovega filtra v primeru, ko meritve za nek daljši čas niso na voljo. Na primeru vozila si lahko predstavljamo, da smo zapeljali v tunel ali sotesko, kjer GPS signal ni na voljo. Kot vidimo na sliki 9, kjer smo izpustili meritve položaja z indeksi \(i \in [850, 950)\), začne v tunelu napoved vedno bolj odstopati od reference. Ko tunel zapustimo in je meritev pozicije spet na voljo, se napoved skokoma popravi.
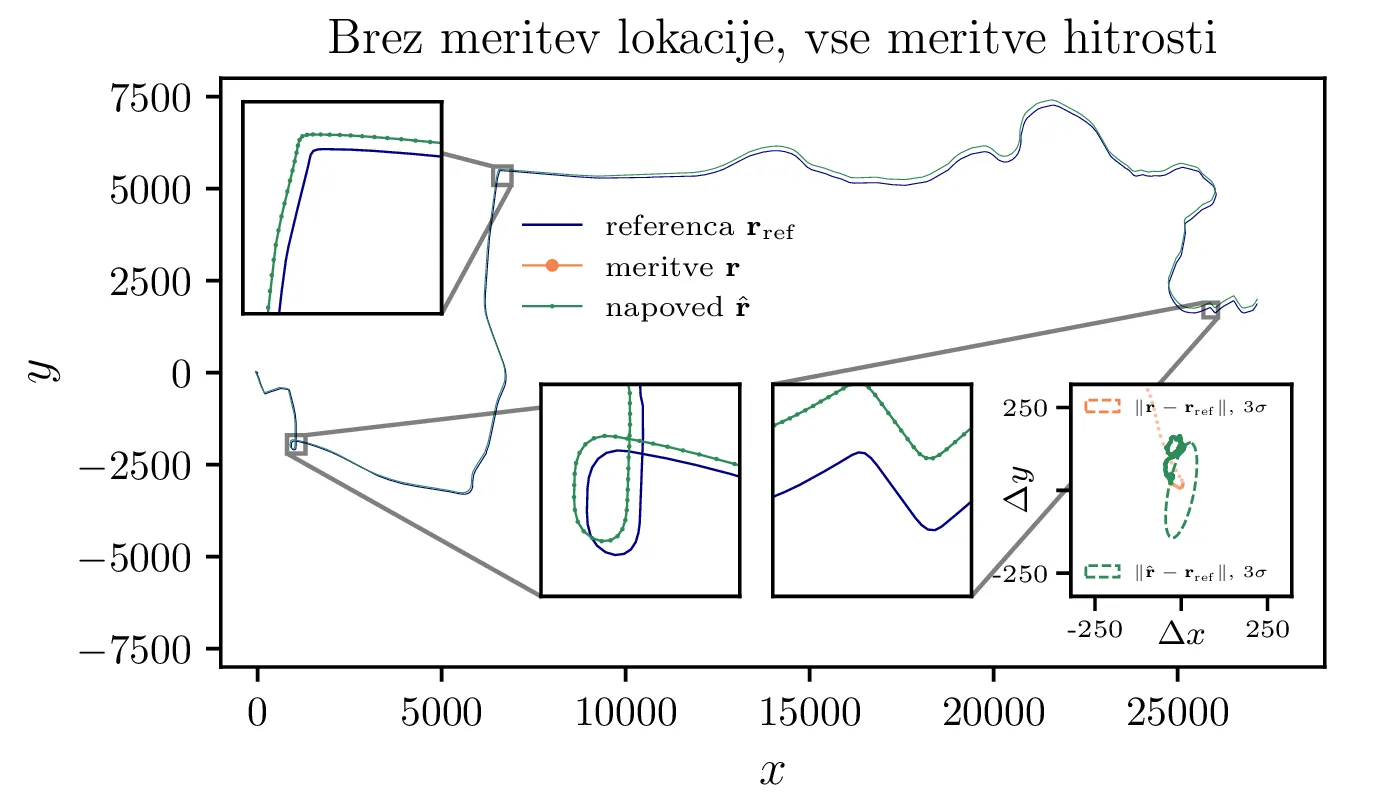
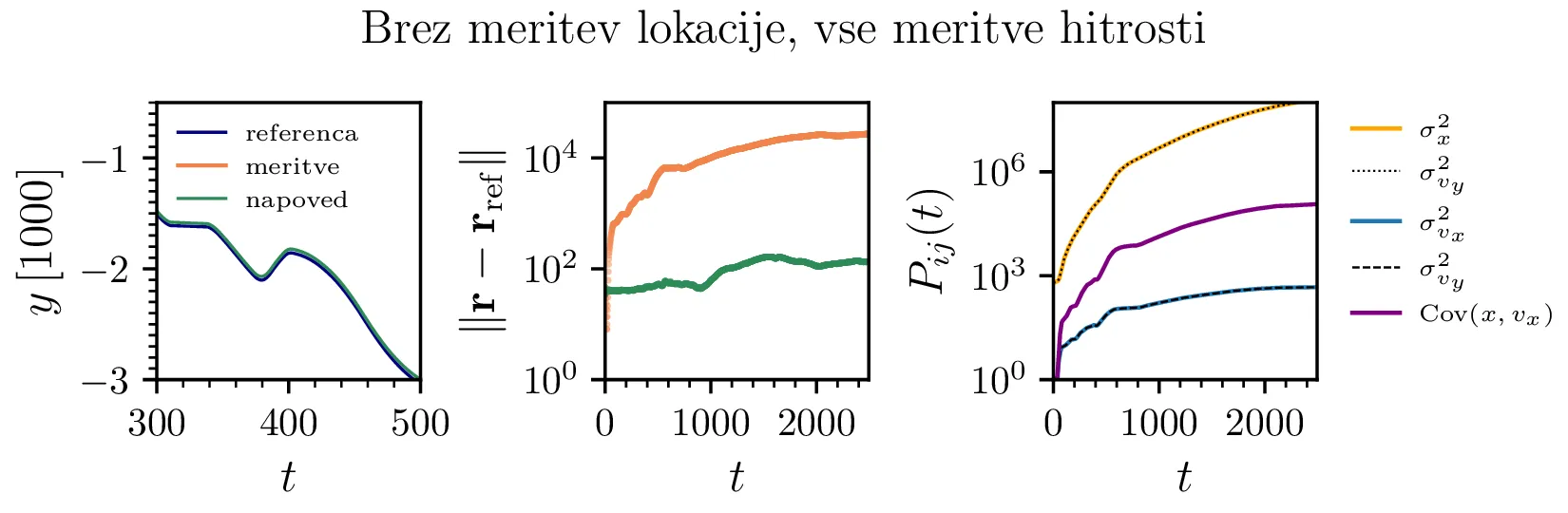
Meritve brez hitrosti oz. položaja
S telefonom lahko merimo le lokacije in pospeške, torej meritev hitrosti nimamo na voljo. Matrika senzorja je torej \[H = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix}.\] Napovedi trajektorije brez meritev hitrosti vidimo na sliki 10. Trajektorija in histogram odstopanj je izjemno podoben tistemu z meritvami hitrosti (t. j. \(H = I_{4\times 4}\)). Potrjujemo torej opažanja slik 4, 5 in 6 – izpuščanje meritev hitrosti ima relativno majhen vpliv, saj jih preko Kalmanovega filtra lahko nadomestijo goste meritve pozicije. V drugem zanimivem scenariju je GPS signal nedostopen, na voljo imamo le meritve hitrosti in pospeška. V takem primeru je matrika senzorja \[H = \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}.\] Na sliki 11 vidimo trajektorijo, napovedano le iz meritev hitrosti in pospeška. Kot smo ponovili že večkrat, je meritev pozicije mnogo "močnejša" in lahko kompenzira manjko meritev hitrosti. Ker pozicij nimamo na voljo, se napake akumulirajo in napoved pozicije postaja s časom vedno manj točna. To vidimo tako v dejanskem odstopanju na sliki 11 sredinsko spodaj in tudi v napovedani napakah, t. j. elementih kovariančne matrike na isti sliki desno spodaj.
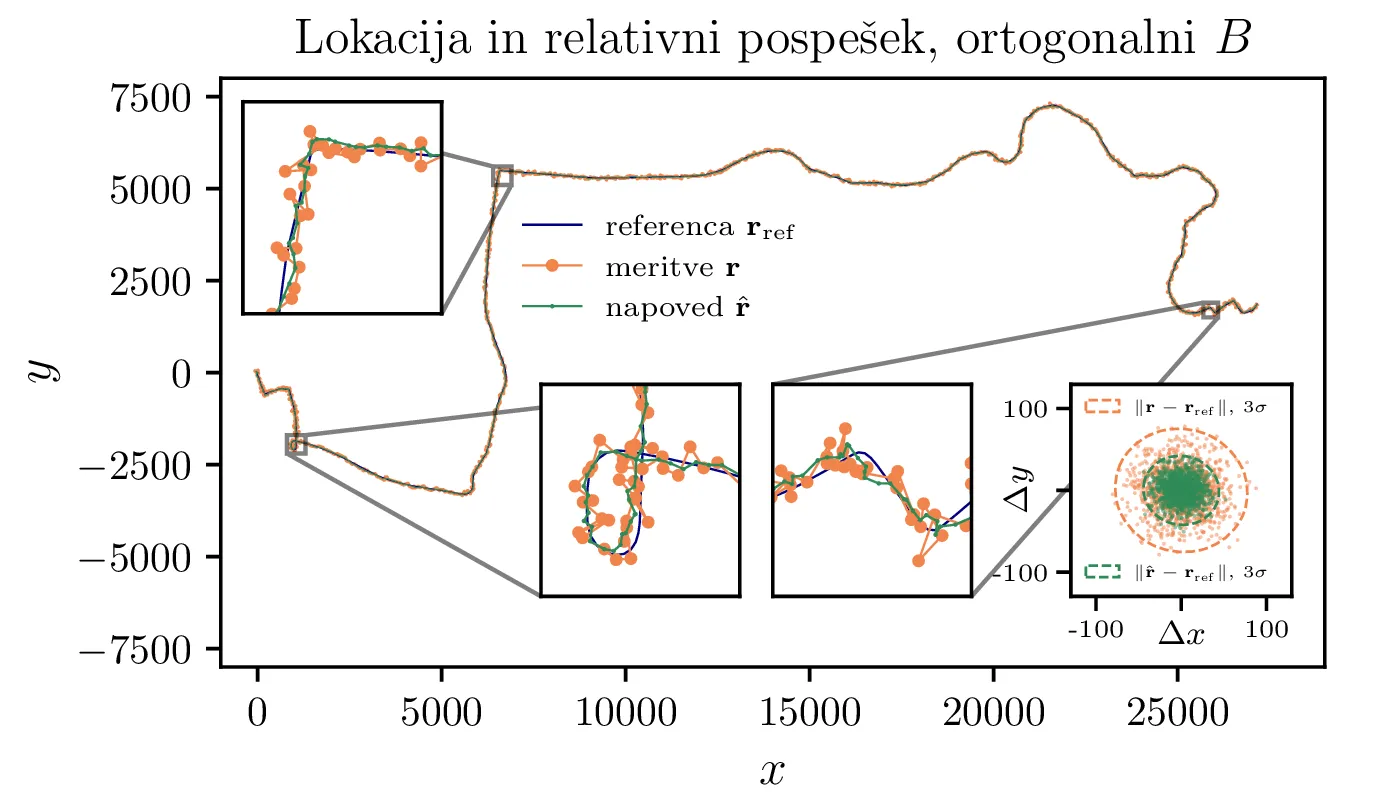
kalman_relative_data.dat. (Levo) Neustrezno transformiran pospešek, kjer relativen pospešek
upoštevamo, kot da je podan v laboratorijskem sistemu
\(\mathbf{a} = \mathbf{a}_\mathrm{rel}\). (Desno) Ustrezno transformiran
relativni pospešek \(\mathbf{a} = B \mathbf{a}_\mathrm{rel}\). Iz histogramov
odstopanj vidimo, da ustrezna transformacija omogoči bolj točno napoved.
Meritve preko relativnega pospeška
Dejanski akcelerometer meri pospešek v lokalnem koordinatnem sistemu. Da jih pravilno upoštevamo v kontrolnem
vektorju procesa 1 je potrebno
izmerjen \(\mathbf{a}_\mathrm{rel}\) transformirati v laboratorijski sistem kot
\(\mathbf{a} = B \mathbf{a}_\mathrm{rel}\), pri čemer je matrika ortogonalne
transformacije
\begin{equation}B = \frac{1}{\| \mathbf{v} \|} \begin{pmatrix} v_x & -v_y \\ v_y & v_x \end{pmatrix},
\label{eq:B}\end{equation}
kovariančna matrika procesnega šuma pa
\[Q^{vv}_{n} = \Delta t^{2} \left\{ \sigma_a^2 I_{2 \times 2} + \frac{\mathbf{v}_n^{\top} P^{vv}_n
\mathbf{v}_n}{\|\mathbf{v}_n\|^4} \left[ \left( B^{vv}_n a^{\perp}_n \right) \otimes \left( B^{vv}_n
a^{\perp}_n \right) \right] \right\}.\]
Na podlagi podatkov pozicije \((x, y)\) in relativnega pospeška
\(\mathbf{a}_\mathrm{rel}\) iz datoteke
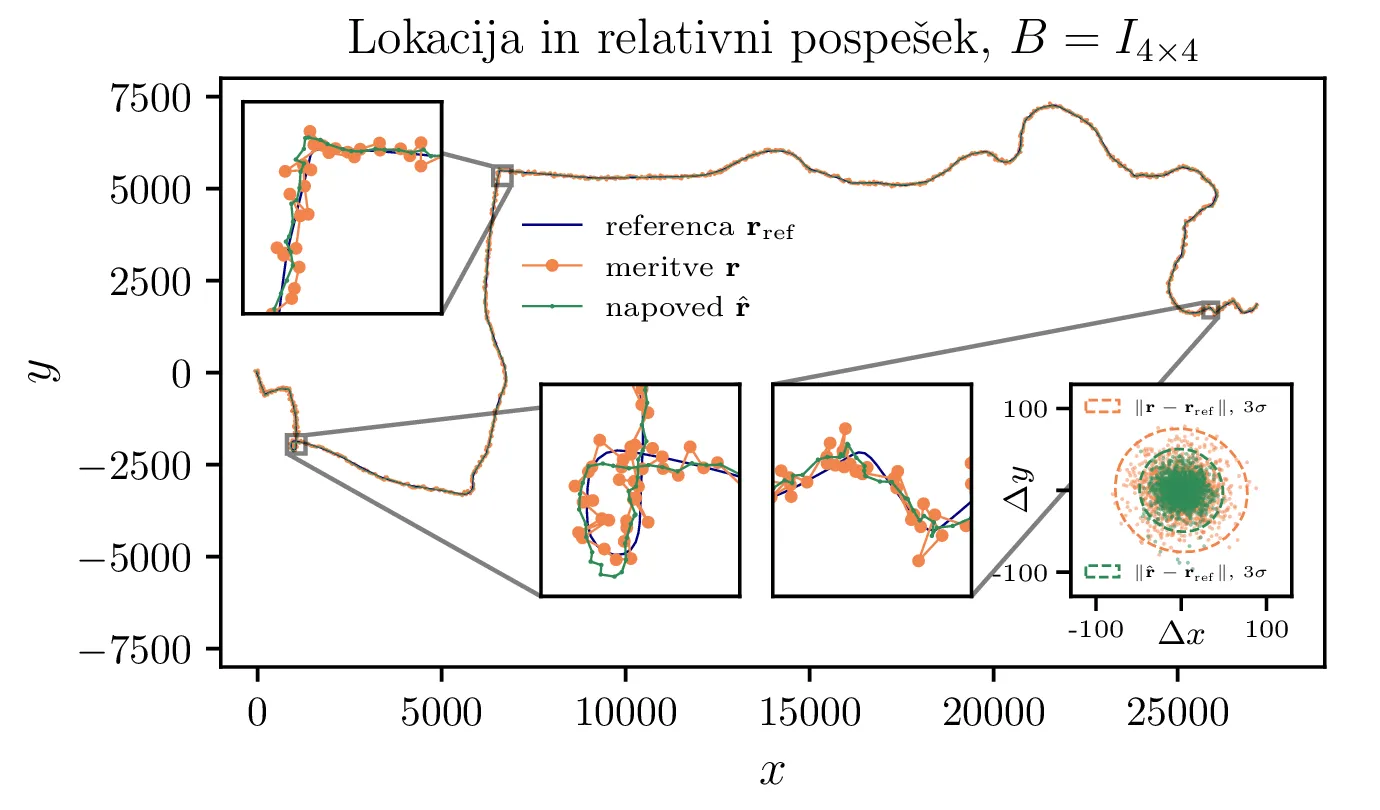
kalman_relative_data.dat lahko zdaj napovemo trajektorijo, kot to vidimo na sliki 12
desno. Na isti sliki levo vidimo še napoved brez uporabe ustrezne ortogonalne transformacije 6. Že na oko, pa tudi preko kvantitativne primerjave v tabeli 1
vidimo, da je kljub popolnoma nesmiselnim pospeškom napoved še vedno precej robustna, saj pospeške spremljajo
dejanske meritve pozicij preko GPS.
| \(\frac{\sigma_1 + \sigma_2}{2}\) | \(\|\sigma_1 - \sigma_2\|\) | \(\pi \sigma_1 \sigma_2\) | \(\frac{\hat{\sigma}_1 + \hat{\sigma}_2}{2}\) | \(\|\hat{\sigma}_1 - \hat{\sigma}_2\|\) | \(\pi \hat{\sigma}_1 \hat{\sigma}_2\) | |
|---|---|---|---|---|---|---|
kalman_cartesian_data, slika 1
|
24.66 | 0.97 | 1910 | 13.36 | 0.60 | 560.6 |
kalman_relative_data, brez preslikave \(B\)
|
25.53 | 1.23 | 2046 | 19.60 | 0.93 | 864.9 |
kalman_relative_data, z preslikavo \(B\)
|
25.53 | 1.23 | 2046 | 14.44 | 0.93 | 654.3 |