Modelska analiza I
10. naloga: Spektralna analiza in filtriranje

Navodila

Signaloma s 512 točkami v datotekah val2.dat in val3.dat določi frekvenčni spekter. Preskusi različne okenske funkcije. Kako se spremeni spekter, če analiziramo krajše intervale (64, 128, …točk)? Signal \(u(t)\), ki prihaja v merilno napravo s prenosno funkcijo \(r(t)\), se ob dodatku šuma n(t) preoblikuje v \[c(t) = u(t) \ast r(t) + n(t) = s(t) + n(t).\] Iz izmerjenega časovnega poteka \(c(t)\) bi radi, ob poznavanju odzivne funkcije r(t) in ob nekaterih predpostavkah o šumu n(t), rekonstruirali vpadni signal u(t). N. Wiener je predlagal naslednjo rešitev, ki sledi iz minimizacije napake po metodi najmanjših kvadratov2. Pred dekonvolucijo je treba transformiranko \(c(f)\) pomnožiti s filtrom, \[\Phi(f) = \frac{|S(f)|^2}{|S(f)|^2 + |N(f)|^2}.\]
S pomočjo Wienerjevega filtra napravi dekonvolucijo signalov na datotekah signal{0,1,3,4}.dat. Število točk v posameznem signalu je 512. Na zadnjih treh datotekah je signalu primešan šum. Prenosna funkcija je \[r(t) = \frac{1}{2\tau} \exp\left(-\frac{|t|}{\tau}\right), \quad \tau = 16.\] V fotografiji imamo pogosto opravka s popačitvami konvolucijske narave: razmazanje zaradi gibanja (motion blur), tresenje objektiva med ekspozicijo, slabo fokusiranje, različne optične aberacije. V primeru, da poznamo prenosno funkcijo (t.i. point spread function), lahko posežemo po dekonvolucijskih metodah, s katerimi lahko do neke mere rekonstruiramo originalno fotografijo, odvisno seveda od zrnatosti fotografije.
Poskusi očistiti podobe Lene (lena_k_n_#.pgm)¹ v arhivu lena_slike.tar.gz, razmazane s tremi znanimi konvolucijskimi jedri: tresoč objektiv (kernel1.pgm), slab fokus (kernel2.pgm) ter uklonska mrežica (kernel3.pgm). Datotekam je primešana različna količina Gaussovega šuma (RMS = 0, 4, 8, 16). Pri filtriranju uporabi Wienerjev filter. Po potrebi je smiselno tudi direktno maskirati okolice valovnih vektorjev, kjer je prenosna funkcija singularna. Upoštevaj tudi, da spektralne metode sliko razumejo v periodičnem smislu, kar ustvari ostre skoke na robu. Ugotovi, ali lahko z okenskimi funkcijami ali razširitvijo slike s konstantnimi vrednostmi zmanjšaš vpliv artefaktov na robu. Poskusi tudi očistiti sliko z dodano periodično motnjo (*_nx.pgm).

Učinek spreminjanje dolžine Dirchletovega okna za sinusno funkcijo in pojav spektralnega uhajanja (ang. *spectral leakage*). Signal je točno enak pri vseh dolžinah okna, preverimo pa učinek zajema še dodatne četrtine (sredinsko) in dodatne polovice (desno) našega periodičnega intervala za vzorčenje (hkrati za \(\sin(5x)\) to ne pomeni spet drug celoštevilski večkratnik periode). Vidimo, da s takim širjenjem okna v spektru pridobimo nove lažne frekvence, ki jih v dejanskem signalu \(\sin(5x)\) ni.

Okenske funkcije

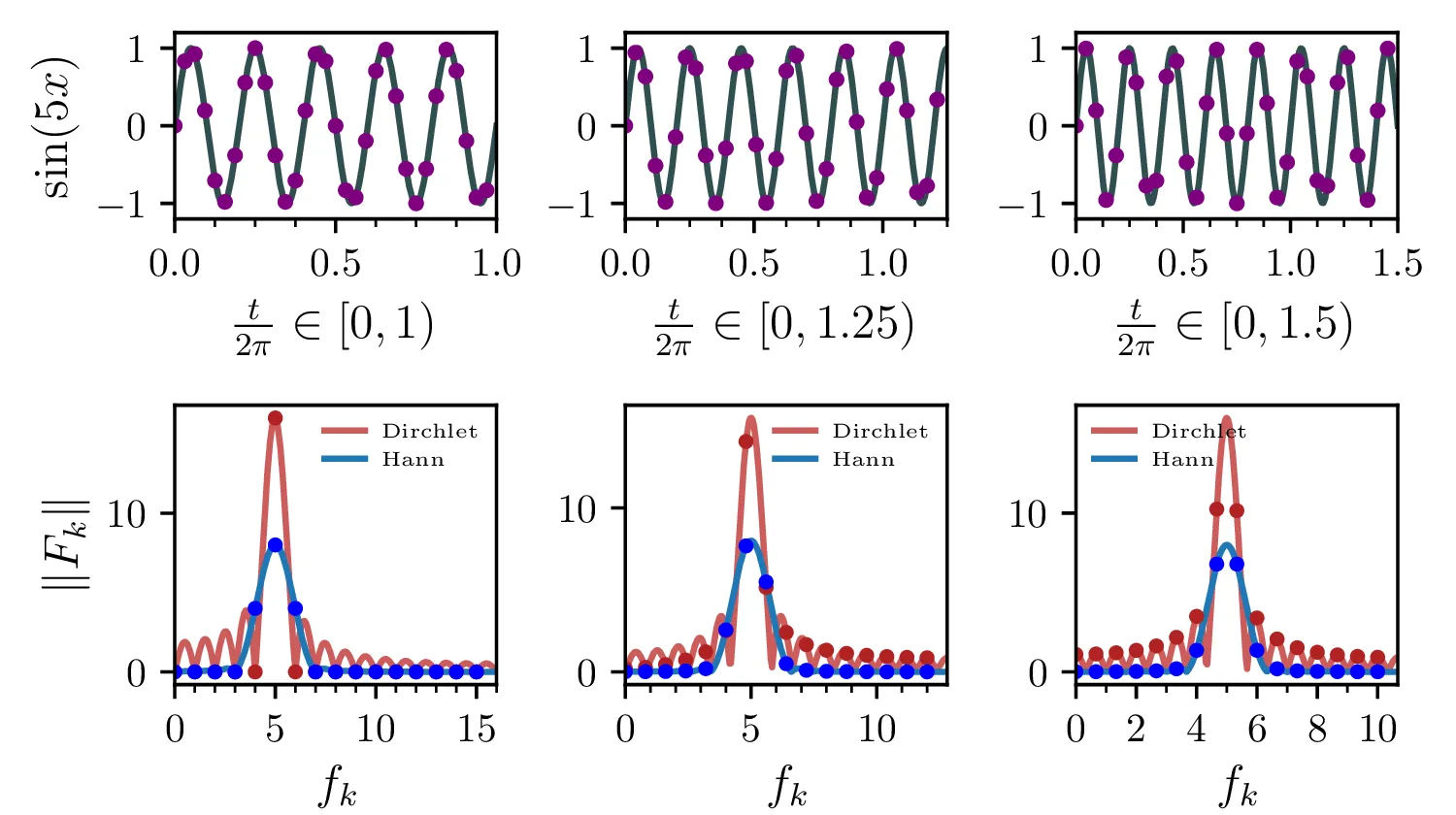
Prvo si poglejmo, kakšen učinek ima na spekter okenska funkcija signala. Najpreprostejši primer kvadratne oz. Dirchletove okenske funkcije vidimo na sliki 1. Vidimo, kaj točno pomeni pojav spektralnega uhajanja, t. j. pojav novih lažnih frekvenc, ki so posledica končnega vzorčenja. Poleg Dirchletove je v uporabi tudi mnogo drugih spektralnih funkcij (glej sliko 2), ki se razlikujejo v tem, kako močno zadušijo spektralno puščanje. Osnovna zahteva za okensko funkcijo je, da ohrani signal v čim večji širini okna, na njegovih robovih pa ima vrednost \(0\).

Kako točno pa se različne okenske funkcije razlikujejo, pa je bolj očitno v frekvenčni domeni (slika 2 sredinsko in desno). Ker z okensko funkcijo signal pomnožimo v časovni domeni, predstavlja to konvolucijo z spektrom okenske funkcije v frekvenčni domeni. Dirchletova okenska funkcija, ki od vseh najbolj močno "pušča", je v frekvenčni domeni preprosto Diracova delta funkcija – konvolucija z njo je identiteta. Okenske funkcije, ki bolj močno zadušijo spektralno puščanje (npr. flat top funkcija) so v frekvenčni domeni širše – konvolucija z takim razširjenim vrhom pa je na nek način zameglitev (ang. blur). Tako okenske funkcije v različnih merah (glede na to kako širok je njihov spekter) zameglijo in zmanjšajo resolucijo spektra, s čimer je efekt puščanja omiljen.

Uporaba okenskih funkcij je posebej relevantna v primerih, kjer želimo spremljati časovno dinamiko nekega spektra. Če bi v nekem namišljenem fizikalnem eksperimentu zajemali signal, sestavljen iz končnega števila harmonskih nihanj (glej sliko 3 in 4), bi bili prisiljeni v uporabo neke okenske funkcije. Dolžino okna nam pogosto določijo zahteve po hitrosti zajemanja ali odzivnosti sistema (če gre za kontrolni sistem). A kot je razvidno na sliki 3, če dolžina te okenske funkcije ni veliko večja od vseh period v merjenem signalu, bi to neizogibno povzročilo spektralno uhajanje.

Prikaz spektralnega puščanja z drsečim oknom. Za dobro definiran signal, ki ima prisotni le dve harmonski komponenti \(\sin(100\cdot2\pi t)\) in \(\sin(150\cdot2\pi t)\). Spektralno puščanje je opazno, močnejše je z krajšim oknom (primerjaj z širšimi okni na sliki 4). Še posebej očitno je pri šibkejšem spektralnem vrhu komponente s frekvenco 150, kjer puščanje močnejšega spektralnega vrha dejansko zamika šibkejši vrh (glej spektre z Dirchletovim oknom). Z drsenjem okna torej frekvenca šibkejšega vrha pleše okoli \(150\). Uporaba primerne okenske funkcije lahko to omili, a če so spektralni vrhovi ob tem preveč razširjeni, lahko dejansko izgubimo možnost razločevanja med njimi. Tako izbira okenske funkcije vedno predstavlja kompromis, saj večja širina okenske funkcije v frekvenčnem prostoru (glej sliko 2) predstavlja izgubo razločevanja med vrhovi. Včasih je torej morda smiselno sprejeti neko stopnjo spektralnega puščanja in ohraniti višjo resolucijo, a le če se zavedamo, da lahko to vpliva na točnost tako določenih frekvenc vrhov.

Širše drseče okno za primerjava z sliko 3. Vidimo, da širše okno zmanjša spektralno puščanje, pričakovano pa hkrati dovoljuje tudi višjo resolucijo za frekvence.

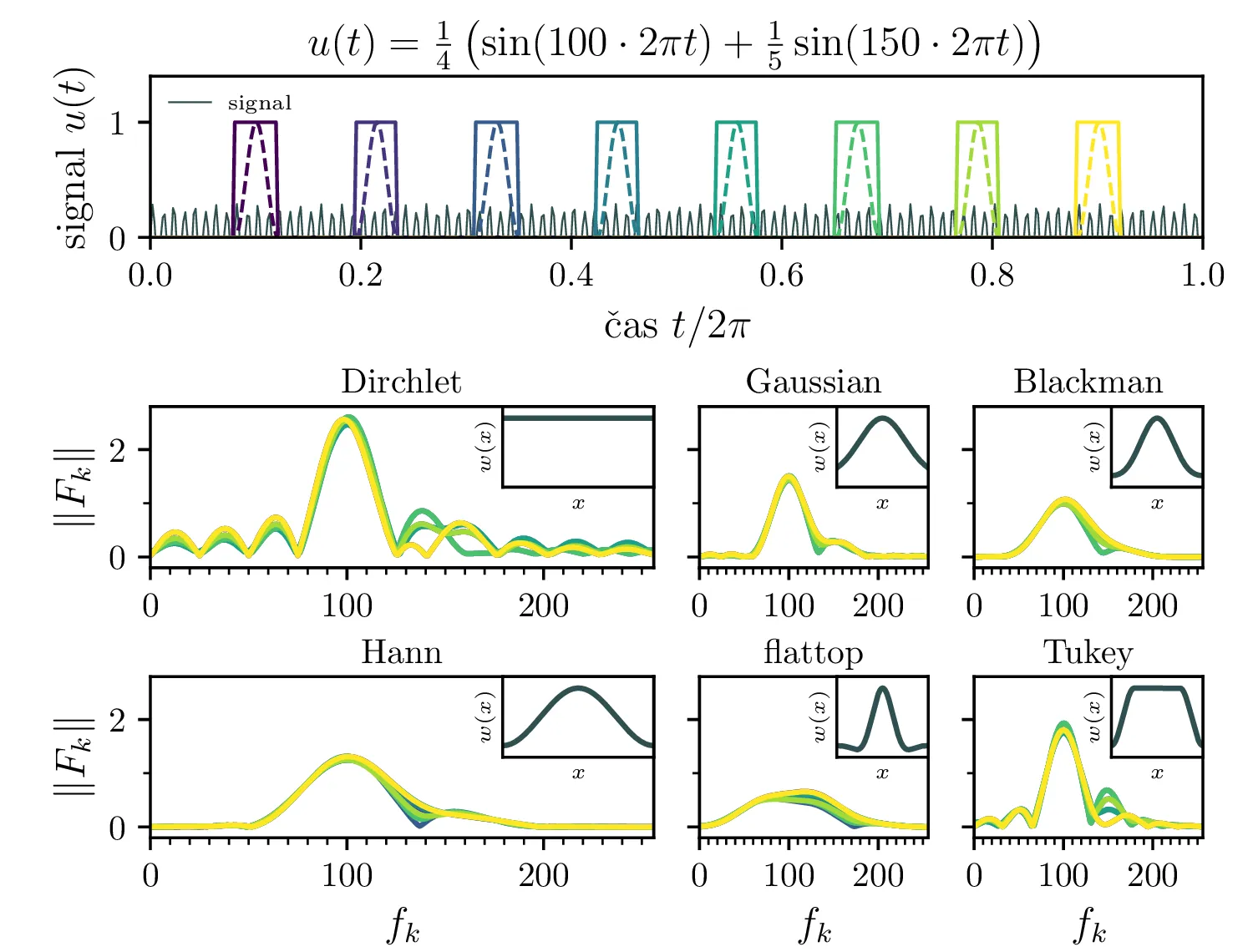
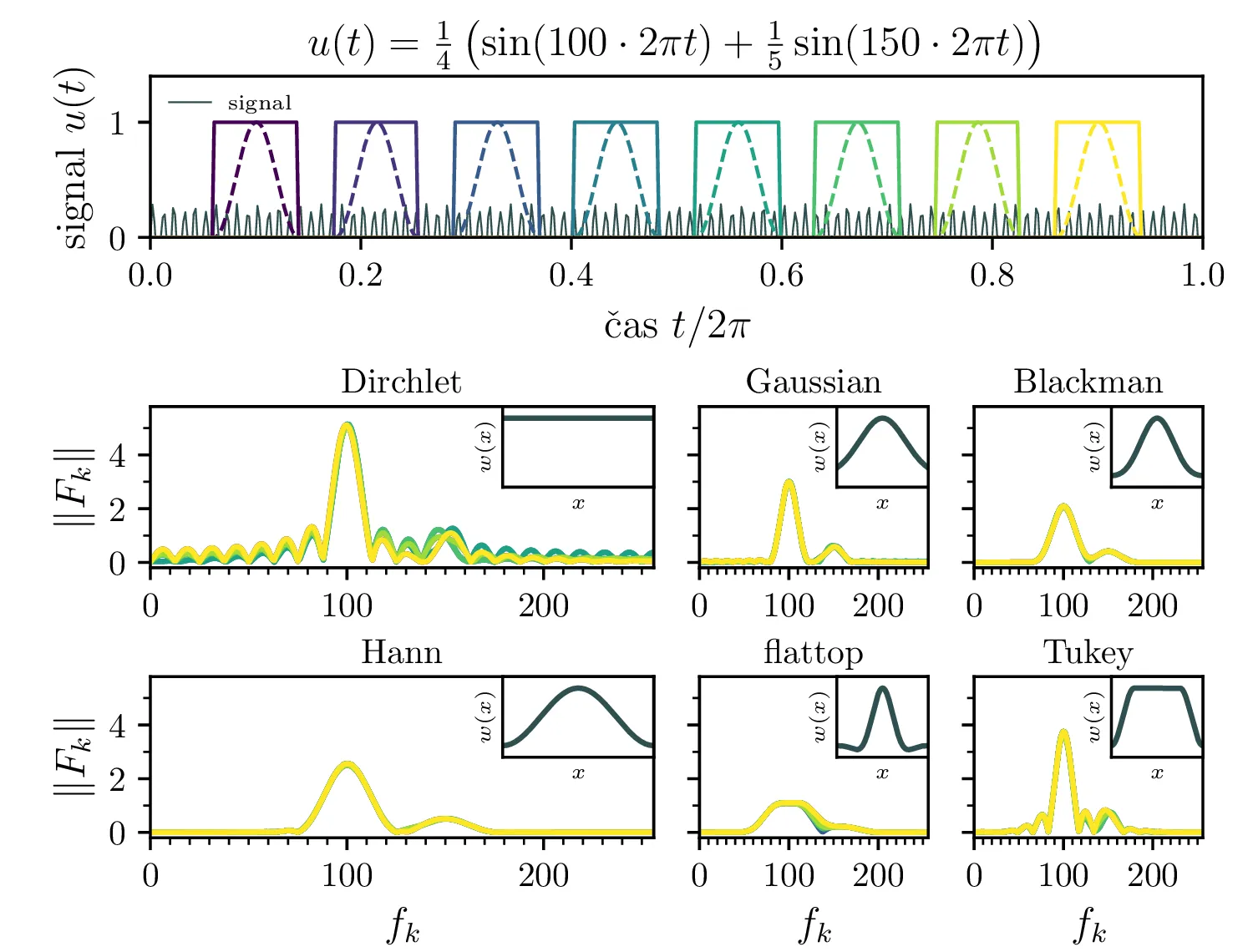
Za signala iz datotek val2.dat in val3.dat (glej sliko 5) poračunamo frekvenčni spekter in si ogledamo vpliv, ki ga ima na spekter uporaba različnih okenskih funkcij.

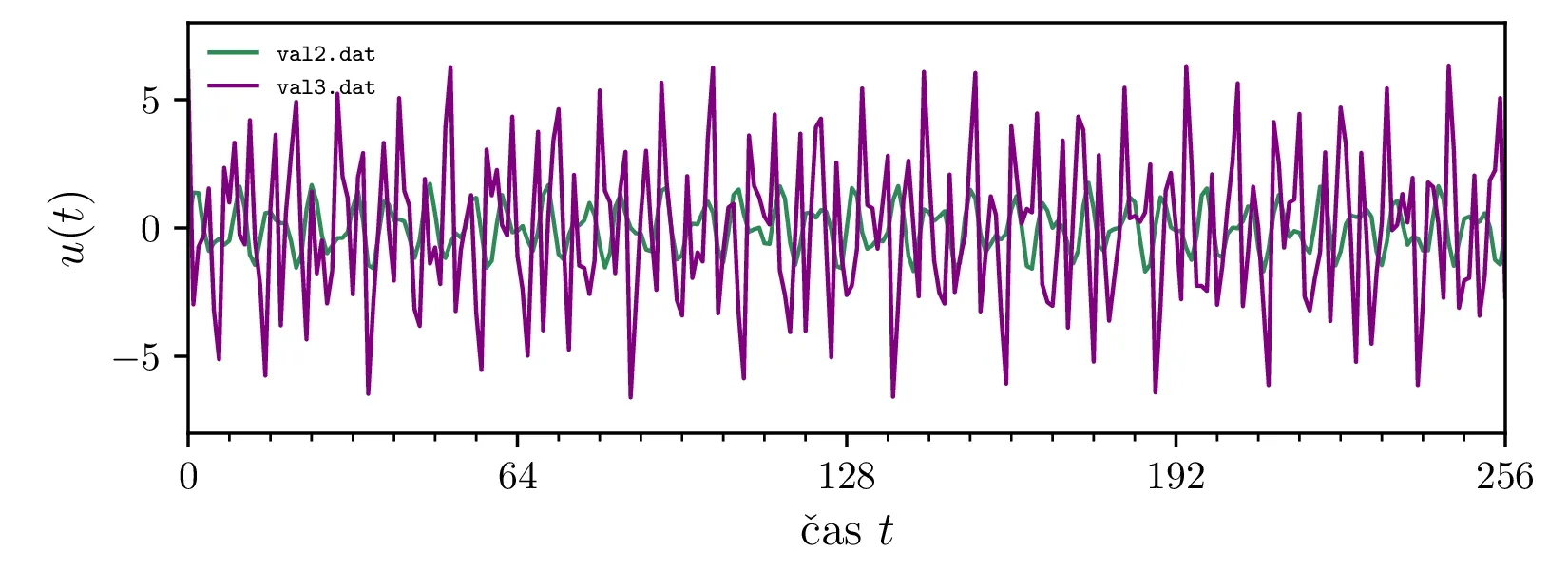
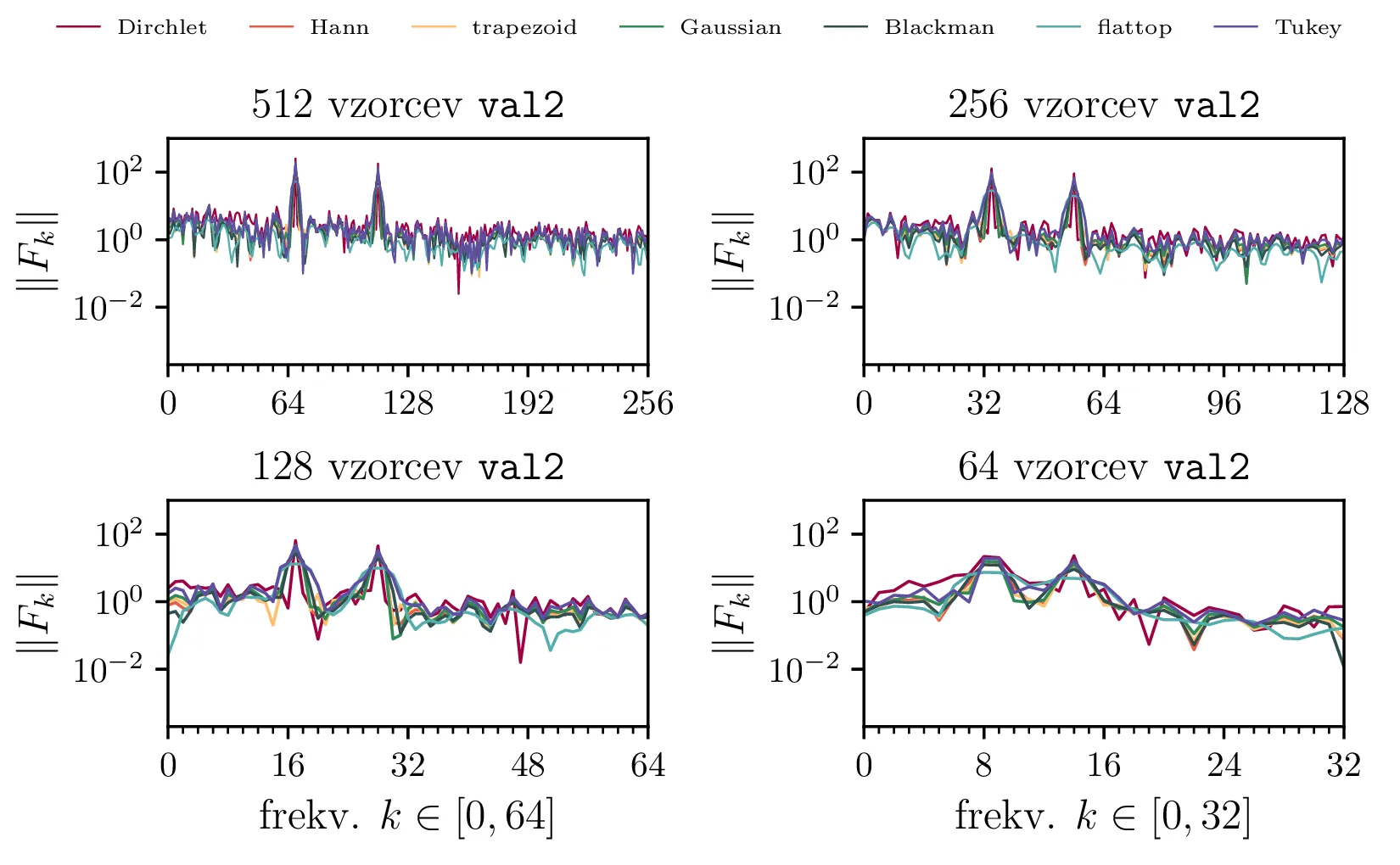
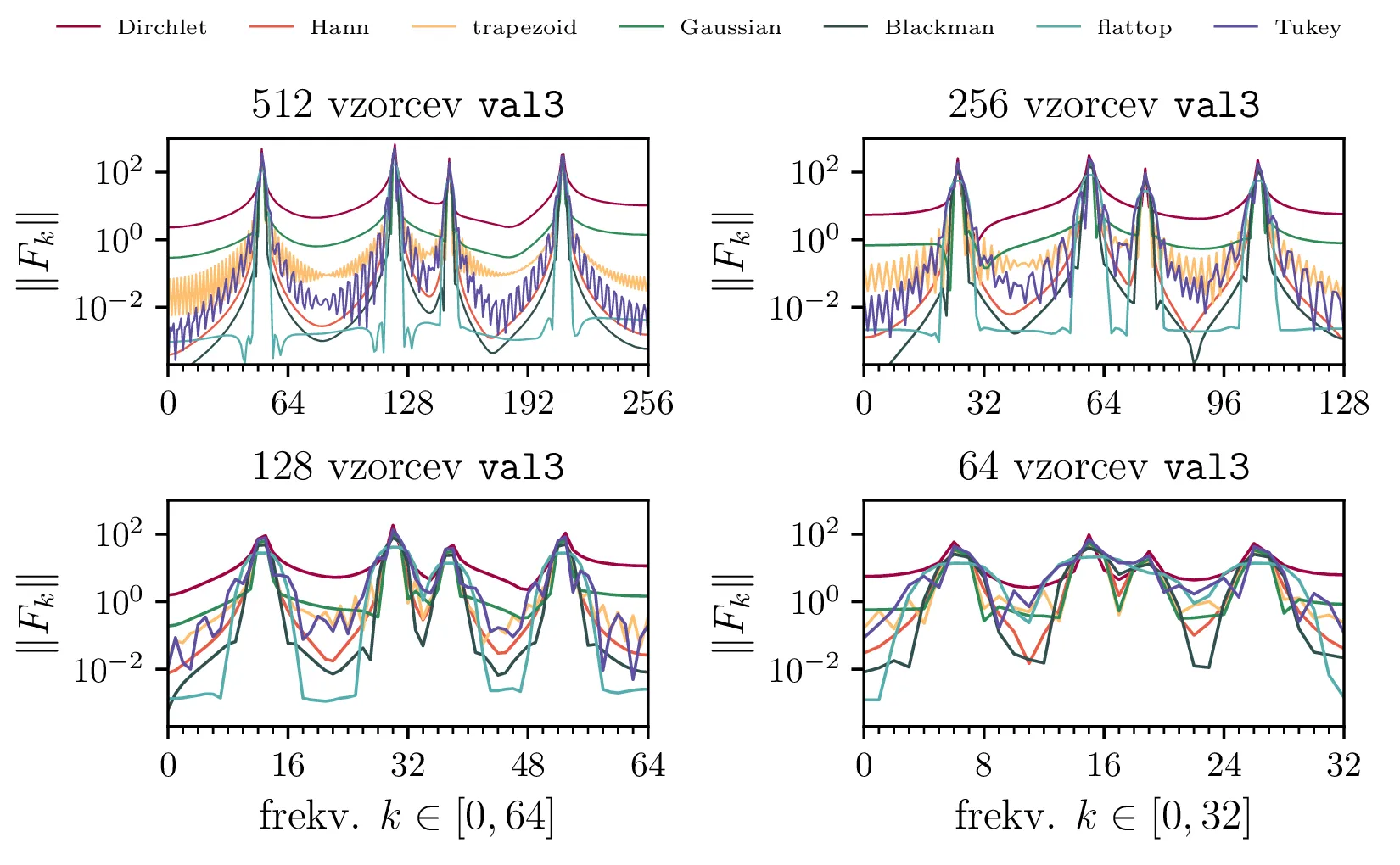
Signala, na katerih preizkušamo okenske funkcije

Spektra signalov `val2` (zgoraj) in `val3` (spodaj) v različnih resolucijah in z uporabo različnih okenskih funkcij. Tudi še na bolj realnem primeru signala vidimo kompromis, ki ga sklepamo z izbiro okenske funkcije; za manjši vpliv puščanja moramo vrhove nujno razširiti, s tem pa znižati efektivno resolucijo našega spektra. Če imamo vzorcev veliko, je tako bolj smiselna uporaba bolj agresivne okenske funkcije (spektralno širše, npr. `flat top` funkcije). Če imamo vzorcev malo, je morda smiselno, da uporabimo nek kompromis, npr. Hannovo okensko funkcijo.

Dekonvolucija v 1D

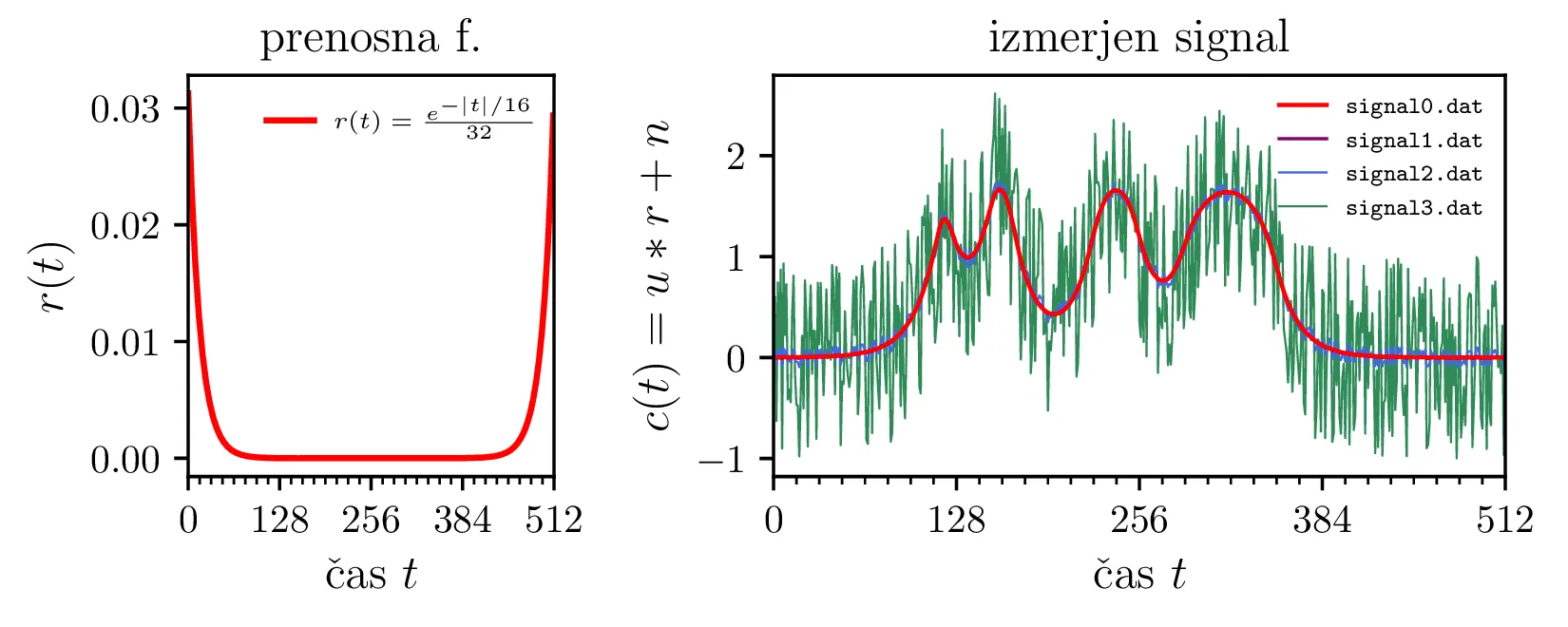
Naši "izmerjeni" signali \(c(t)\) so konvolvirani in zašumljeni (glej sliko 7), tako da je \(c(t) = u(t) \ast r(t) + n(t)\), kjer je člen \(n(t)\) šum. Če bi šuma ne bilo, bi lahko iz \(c(t)\) s poznavanjem konvolucijskega jedra \(r(t)\) (slika 7 levo) preprosto rekonstruiramo signal, tako da bi v frekvenčni domeni delimo z spektrom jedra \begin{equation}u(t) = \mathop{\mathrm{IDFT}} \left\{ \frac{ \mathop{\mathrm{DFT}} \{ c(t) \} }{R(k)} \right\}, \quad R(k) = \mathop{\mathrm{DFT}} \{ r(t) \} \label{eq:naive-deconvolution}\end{equation} To dejansko deluje na signalu signal0, ki nima dodanega šuma (slika 8 levo), povsem propade pa na signalih signal{1,2,3}, ki imajo dodan znaten šum. Kot vidimo na sliki 8 desno, kjer naivno dekonvolucijo napravimo na zašumljenih signalih je ta približek izjemno občutljiv na šum in že majhen neničelen šum \(n(t)\) rekonstrukcijo močno popači. t Zašumljene signale želimo dekonvolvirati, a zaradi visoke občutljivosti na šum so rekonstrukcije neuporabne. V spektru konvolviranih in zašumljenih signalov (slika 9 desno), opazimo Močne vrh pri nižjih frekvencah (recimo \(k < 64\)), ki predstavlja izvorni nezašumljen signal \(u(t)\), ta prispevek signala k spektru poimenujemo \(S(k)\). Poleg tega močnega vrha je prisoten konstanten člen šuma \(N(k)\). Ker imamo pogosto opravka z konvolucijskimi jedri, ki so relativno ozka v frekvenčnem prostoru (to je res tudi za naše jedro, slika 9 levo), bo deljenje z \(R(k)\) konstanten člen šuma \(N(k)\) močno ojačalo pri visokih frekvencah. Očitno je torej, da potrebujemo postopek spremeniti tako, da se šuma pri visokih frekvencah znebimo.

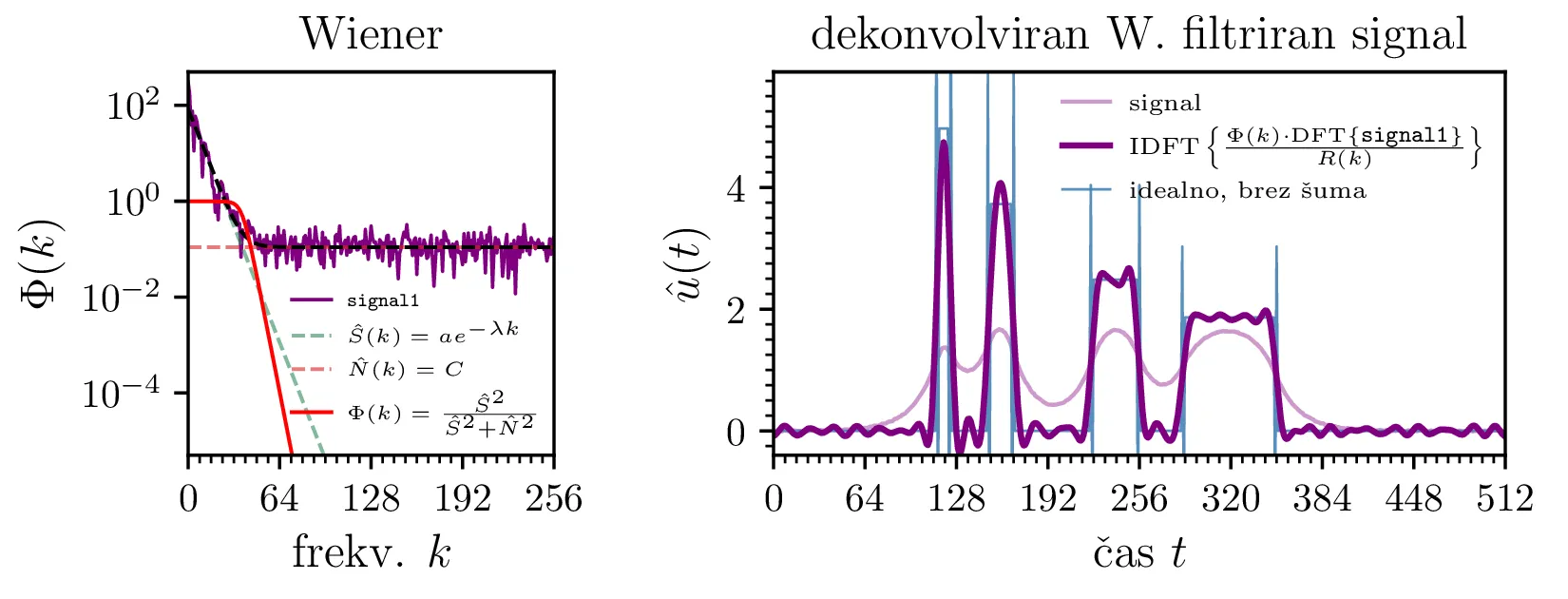
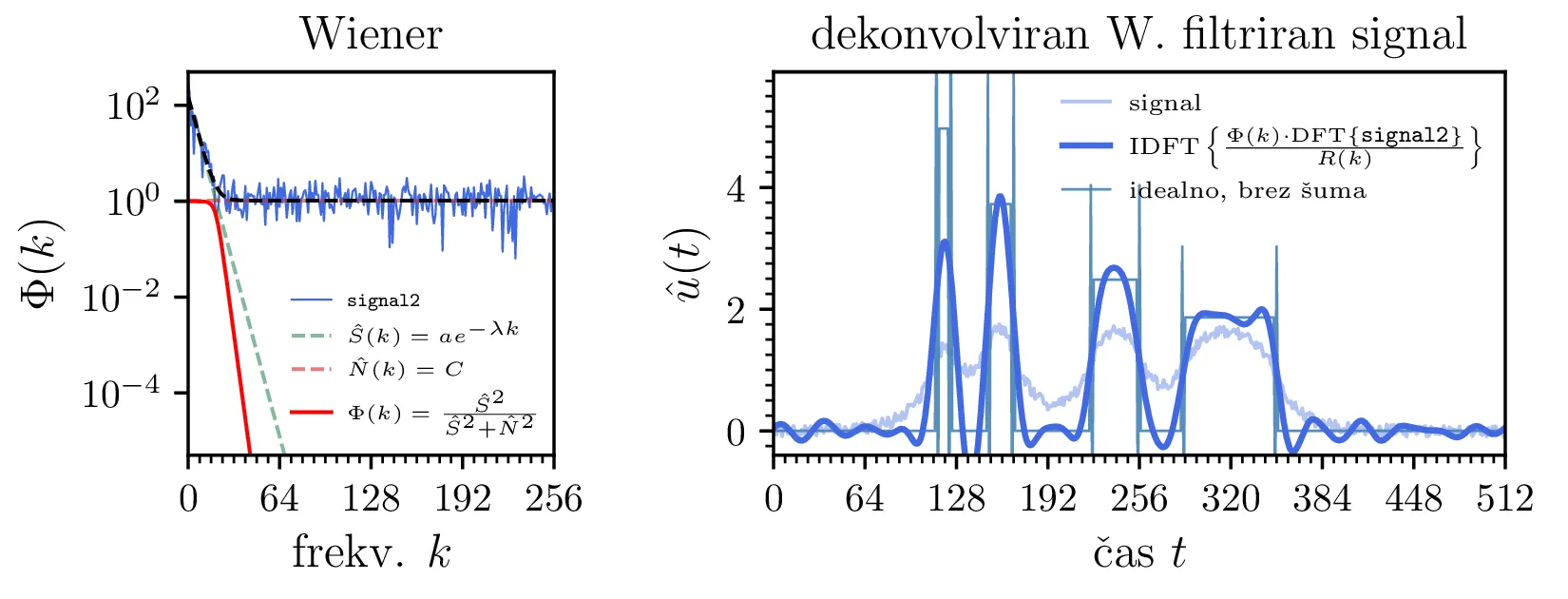
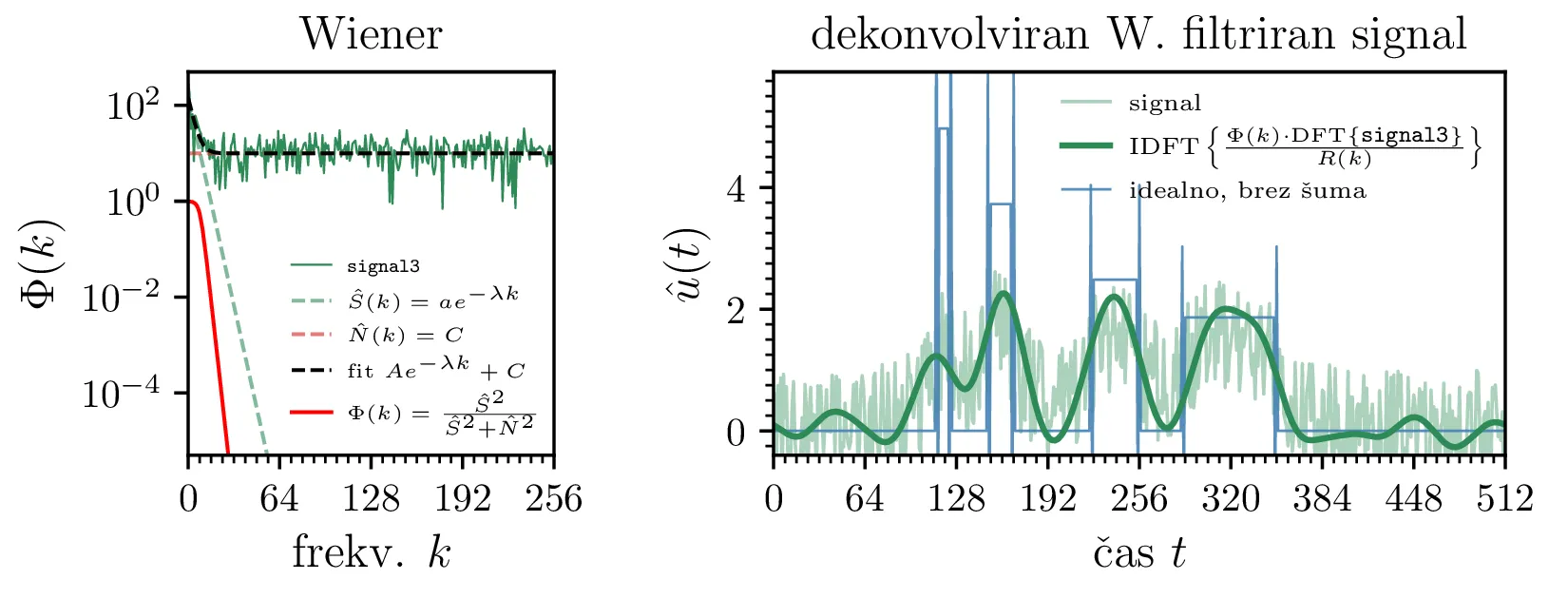
Preprost postopek, ki si bi ga lahko izbrali, bi bila vizualna ocena (glej sliko 9 desno), primerne frekvence, do katere signal \(S(k)\) še prevladuje nad konstantnim pragom šuma \(N(k)\); na podlagi izbrane frekvence bi spekter nad to frekvenco porezali. Nekoliko bolj sofisticiran način, ki se ga bomo poslužili sami, je konstrukcija t. i. Weinerjevega filtra, za katerega se da pokazati, da je ob poznavanju \(S(k)\) in \(N(k)\) optimalen v smislu najmanjših kvadratov odstopanja od idealne rekonstrukcije. Z Weinerjevim filtrom je rekonstrukcija izvornega signala \begin{equation}\hat{u}(t) = \mathop{\mathrm{IDFT}} \left\{ \frac{ \Phi(k) \cdot \mathop{\mathrm{DFT}} \{ c(t) \} }{R(k)} \right\}, \label{eq:Weiner-reconstruction}\end{equation} pri čemer je \(\Phi(k)\) prav Weinerjev filter v frekvenčnem prostoru \begin{equation}\Phi(k) = \frac{\hat{S}(k)^2}{\hat{S}(k)^2 + \hat{N}(k)^2}, \label{eq:Weiner}\end{equation} pri čemer smo z \(\hat{S}(k)\) in \(\hat{N}(k)\) označili naši oceni za člen signala \(S(k)\) in člen šuma \(N(k)\). Ti oceni nista eksaktni, zato tudi filter ni povsem optimalen v prej omenjenem smislu, a rezultat rekonstrukcije je vseeno precej robusten. Za izračun primernih ocen \(\hat{S}(k)\) in \(\hat{N}(k)\) smo spektralno moč razdelil na dva člena \(||C(k)|| = S(k) + N(k)\), modelirana z funkcijama preproste oblike, ki ju po najmanjših kvadratih v logaritemskem prostoru² prilagodimo na spektre zašumljenih konvolviranih signalov (slika 9 desno) \[||C(k)|| \sim Ae^{-\lambda k} + C, \quad \text{fit na spekter zašum. signala},\] tako da je prvi eksponenten modelski člen pripadajoč signalu, drugi pa konstantnemu prispevku belega šuma \[\hat{S}(k) = A^{-\lambda k}, \quad \hat{N}(k) = C.\] S tema ocenama za \(\hat{S}(k)\) in \(\hat{N}(k)\) nato skonstruiramo Weinerjev filter in rekonstruiramo izvorne signale po izrazu 2. Ocene \(\hat{S}(k)\) in \(\hat{N}(k)\) in iz njih konstruirane Weinerjeve filtre \(\Phi(k)\) vidimo na slikah 10 levo. Na istih slikah desno pa vidimo pripadajoče rezultate rekonstrukcije \(\hat{u}(t)\).

(Levo) Prenosna funkcija \(r(t) = \frac{1}{2\tau} e^{-|t|/\tau}\) za \(\tau = 16\), vzorčena na periodičnih \(512\) vzorcih. (Desno) "Izmerjeni" signali \(c(t)\), ki so konvolvirani in zašumljeni, tako da je \(c(t) = u(t) \ast r(t) + n(t)\), kjer je člen \(n(t)\) šum; za signal `signal0` je ta člen enak 0, za signale `signal{1,2,3}` pa je vedno večji.

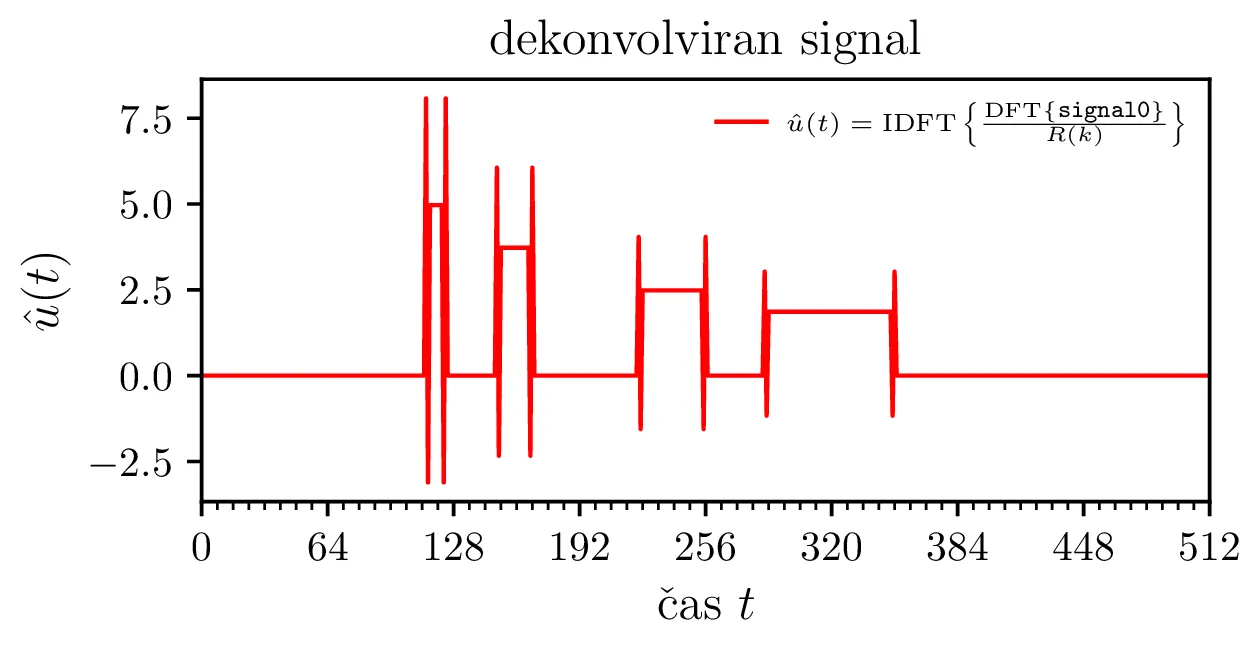
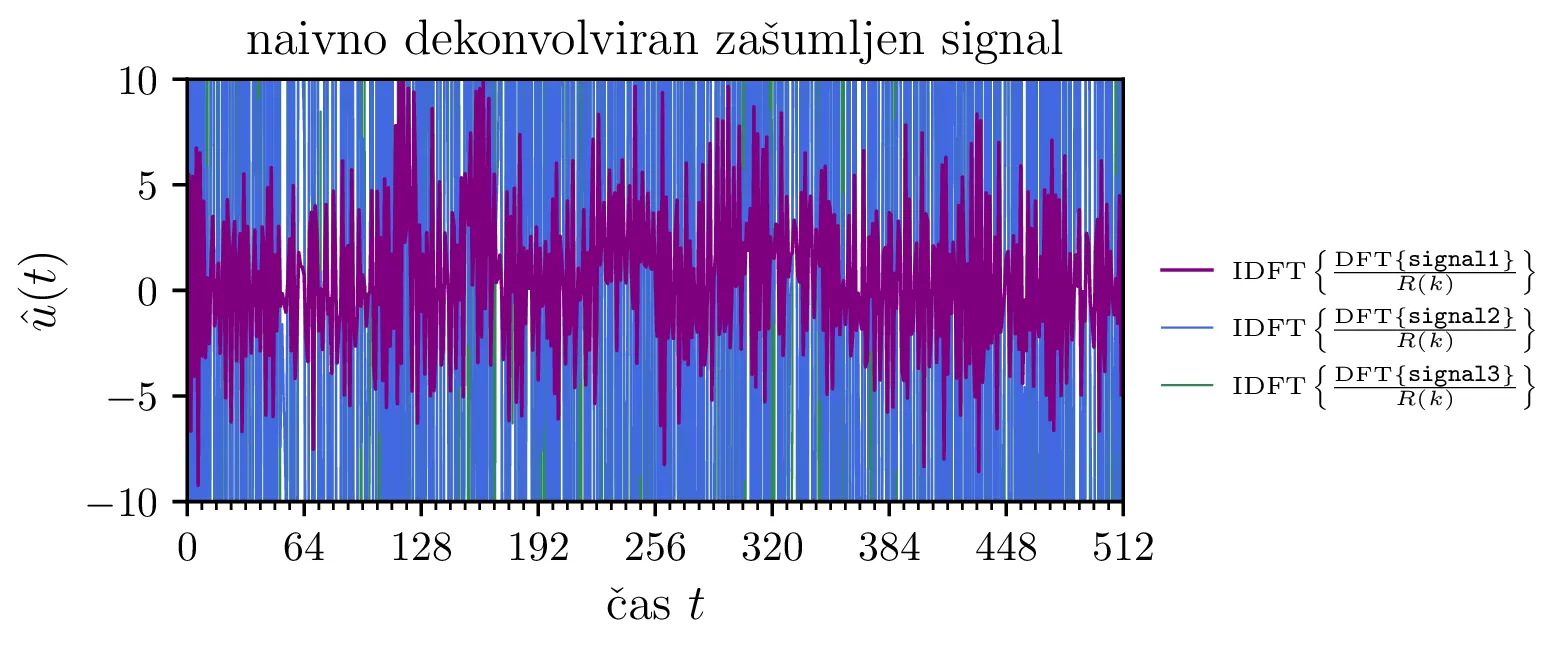
(Levo) Dekonvolviran signal `signal0` po izrazu 1. Rekonstrukcija je točna do natančnosti računalniške aritmetike, saj signal ne vsebuje nobenega dodanega šuma. (Desno) Na enak način dekonvolvirani signali `signal{1,2,3}`, ki imajo dodan neničelen šum. Zaradi ojačanja šuma pri visokih frekvencah je že za `signal1`, ki ima dodan precej majhen šum, rekonstrukcija zelo močno zašumljena in zato praktično neuporabna.

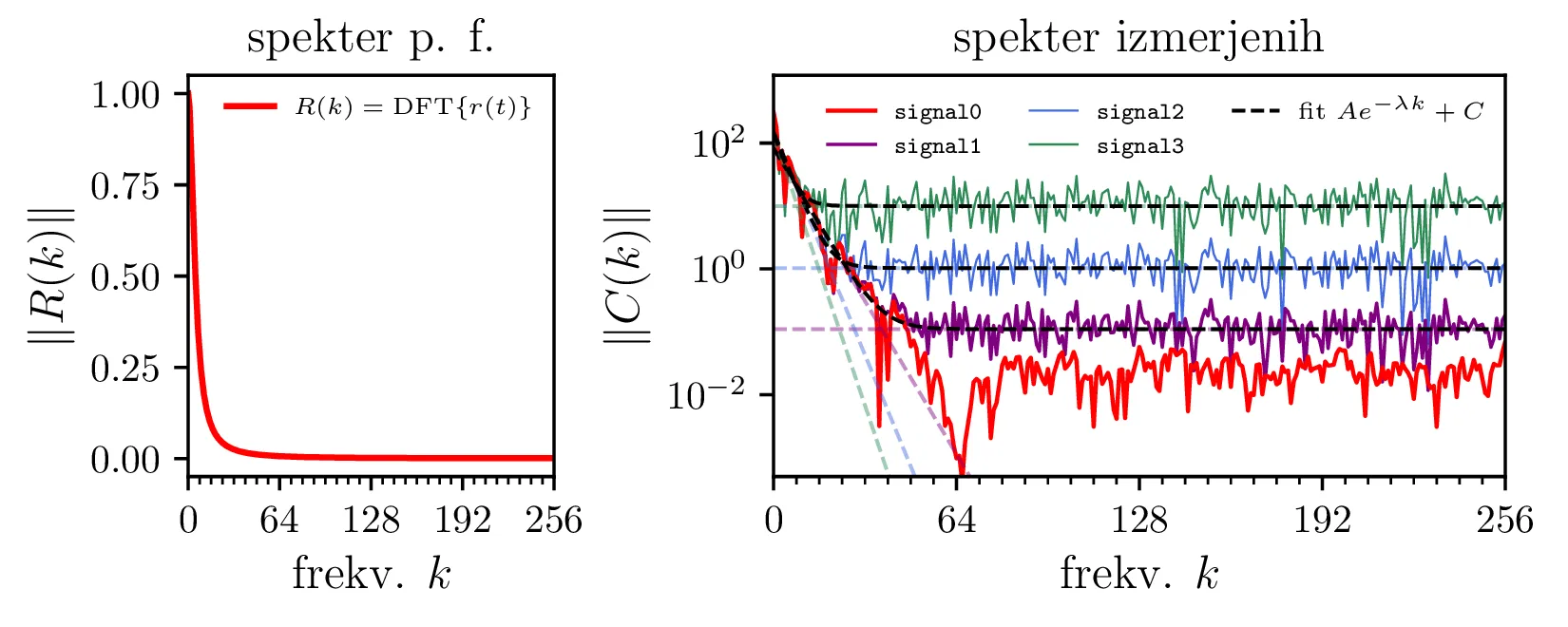
(Levo) Spekter prenosne funkcije \(\propto \frac{1}{1 + \tau^2 \omega^2}\), kjer je \(\omega = 2\pi k\). (Desno) spektri signalov `signal{0,1,2,3}`. S črtno črtkano črto je narisan fit \(Ae^{-\lambda k} + C\) na spekter zašumljenih konvolviranih signalov. Črtkano v barvah sta narisana posamezna člena \(\hat{S}(k) = Ae^{-\lambda k}\) in \(\hat{N}(k) = C\) v fitu.

(Levo) Spektri signalov \(c(t)\) in ocene člena za signal \(\hat{S}(k)\) in člena šuma \(\hat{N}(k)\) iz fita na spekter. Z oranžno polno črto so narisani iz ocen konstruirani Weinerjevi filtri, ki močno zadušijo visokofrekvenčen šum, ohranijo pa nizkofrekvenčne prispevke, ki prevladujejo nad šumom. (Desno) Pripadajoče rekonstrukcije \(\hat{u}(t)\) z uporabo konstruiranih Wienerjevih filtrov. Vidimo, da rekonstrukcija ni močno zašumljena. Ko večamo amplitudo šuma v "izmerjenem" signalu postaja rekonstrukcija vedno bolj zglajena, saj Wienerjev filter poreže vedno več frekvenc. Signal lahko torej rekonstruiramo le do tistega frekvenčnega praga, kjer so spektralne komponente še močnejše od šuma. Efekt je torej podoben, če bi imeli na voljo manjše število nezašumljenih vzorcev, npr. z umetni združevanjem ali bolj fizikalno s tem, da bi za nek senzor (npr. piksel CCD kamere) povečali čas zajemanja.

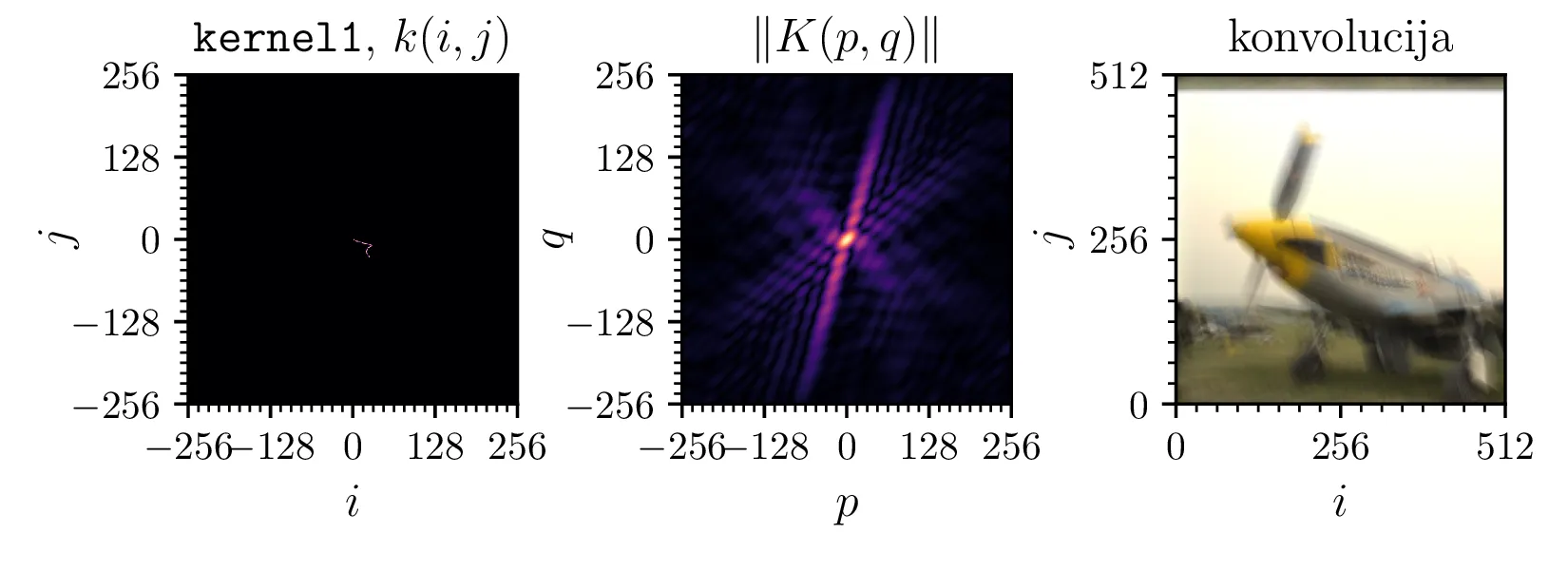
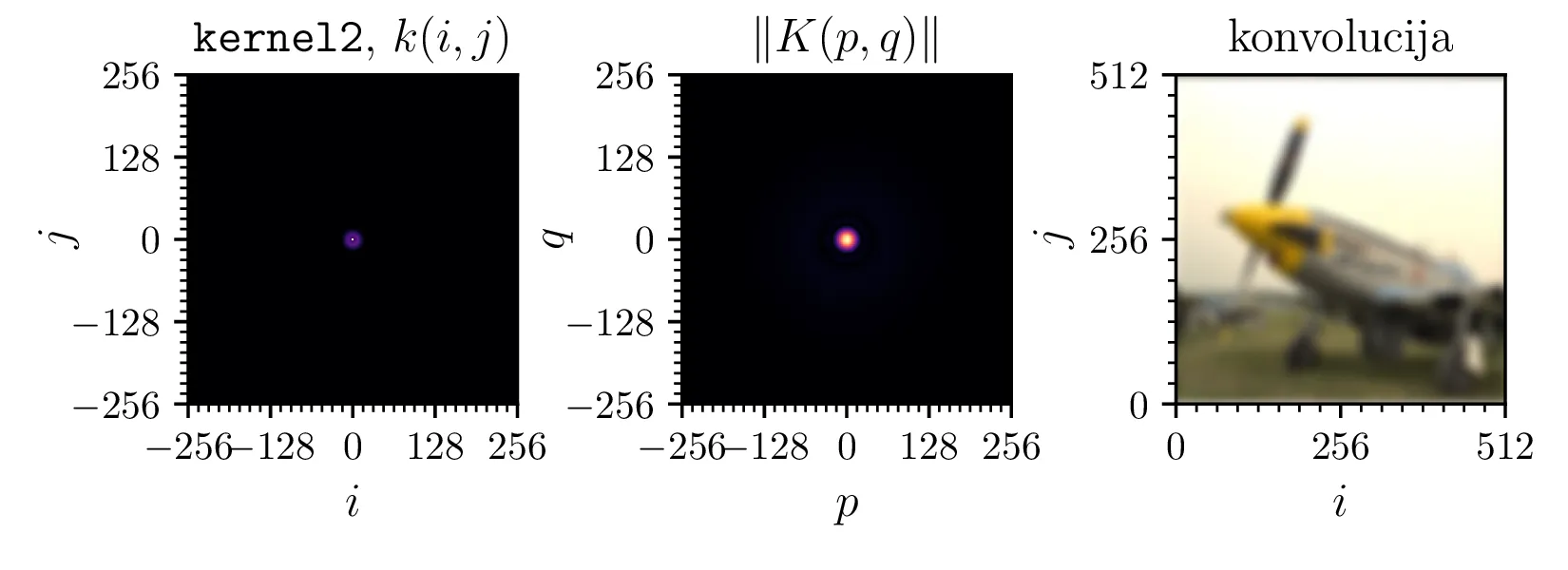
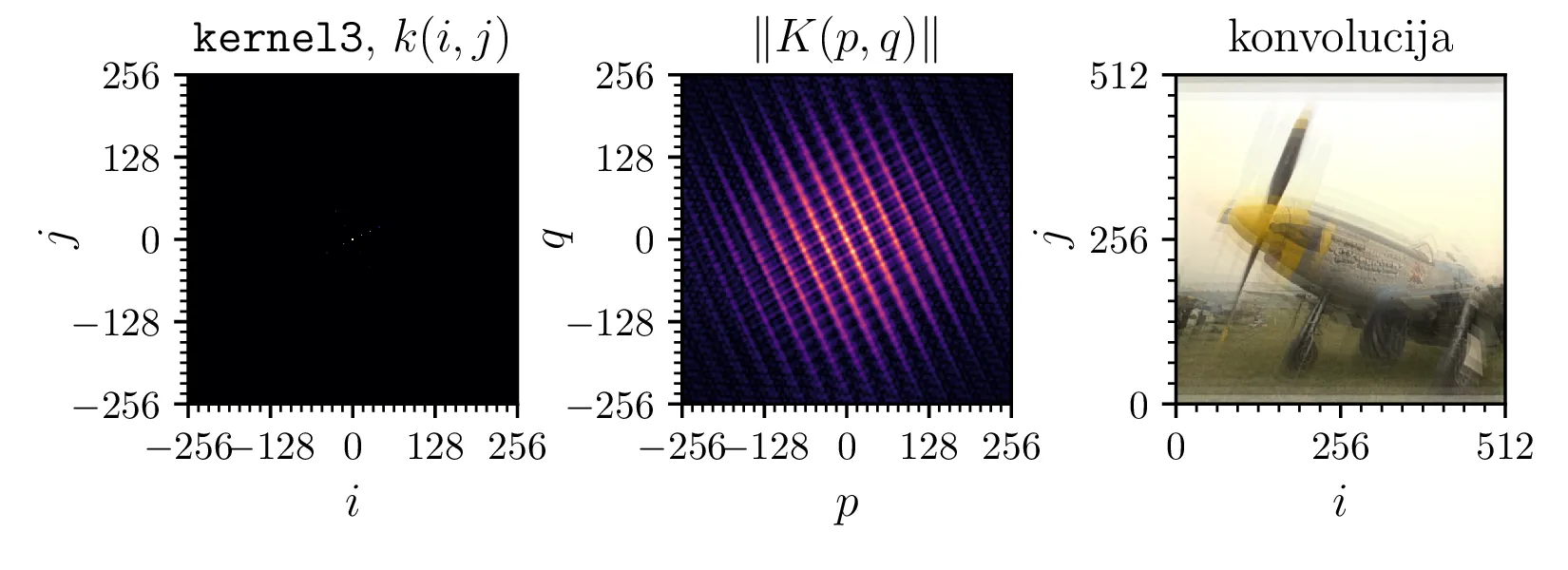
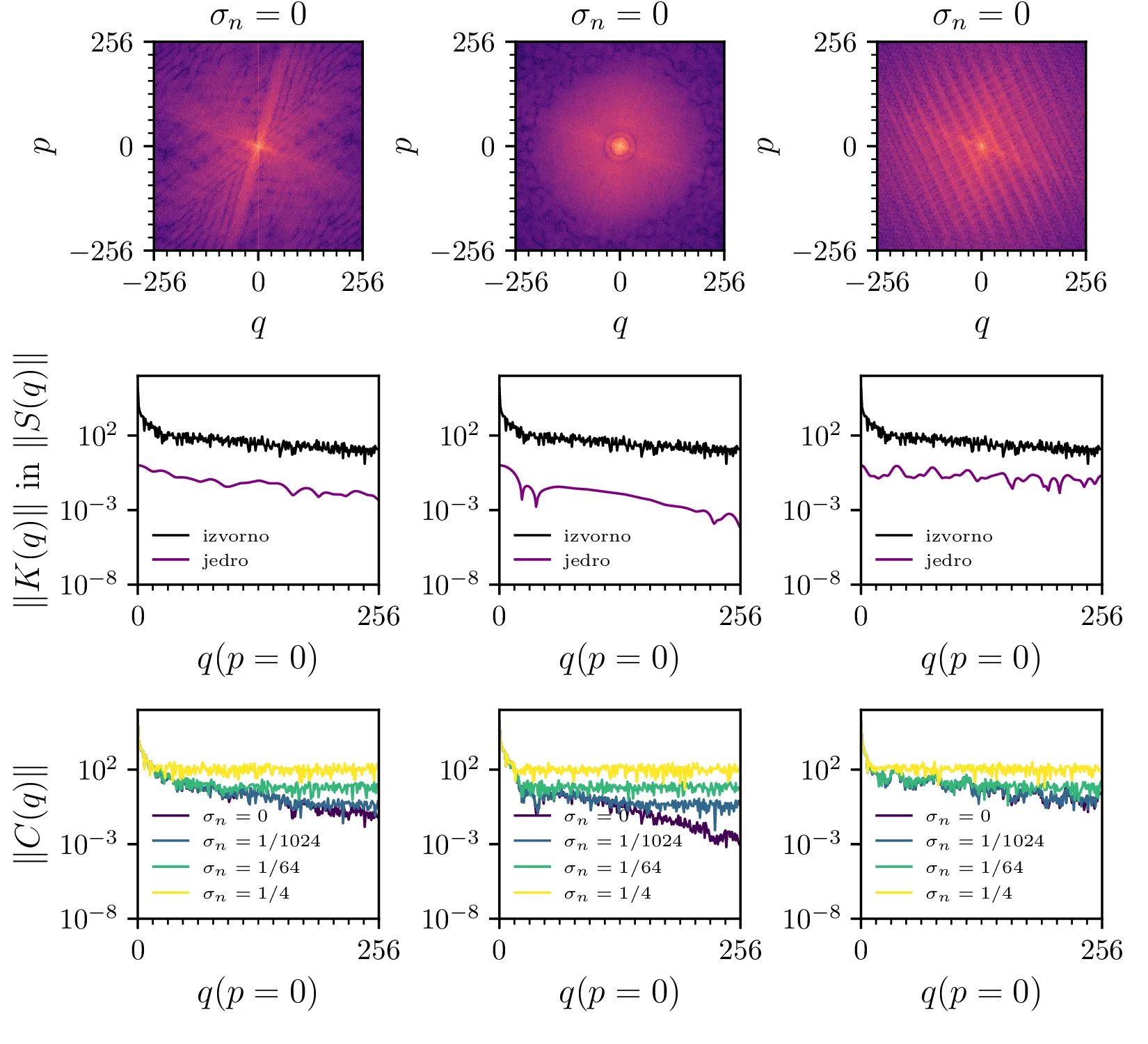
(Levo) Konvolucijska jedra `kernel{1,2,3}`, ki predstavljajo tresoč objektiv, slab fokus (ang. *blur*) in uklonsko mrežico. (Sredinsko) Spekter (spektralna moč) jeder. (Desno) Slika, konvolvirana z posameznim jedrom.

(Zgoraj) Spekter \(\| C(p, q) \|\) konvolviranega signala brez dodanega šuma, v logaritemski skali. Vidimo jasen vrh visokih amplitud v osrednjem delu, pri nizkih frekvencah \(p, q\). (Sredinsko) Preseka \(p = 0\) spektralnih moči izvornega signala \(\| S(p, q) \|\) (črno) in konvolucijskega jedra \(\| K(p, q) \|\). Teh dveh oblik tipično ne poznamo, zmnoženi sta pravzaprav kar spekter \(\| C(p, q) \|\). Narekujeta model, ki ga prilagajamo na spekter konvolviranega in zašumljenega signala, zato v 14 člen \(\hat{S}\) nastavimo kar kot produkt eksponentnega pojemanja od središča in znanega spektra jedra \(\| K(p, q) \|\). (Spodaj) Preseki spektrov konvolviranega in zašumljenega signala \(\| C(p, q) \|\). Vidimo, kako v spektru raste prag šuma, ko večamo amplitudo dodanega šuma.

Dekonvolucija v 2D

V dveh dimenzijah so postopki povsem analogni tistim v eni dimenziji, le da časovno koordinato signal \(t\) zamenjamo z koordinatama pikslov \((i, j)\), frekvenco \(k\) pa z valovnim vektorjem \((p, q)\). Dodatna kompleksnost je le v smiselni izbiri nastavkov za Wienerjev filter, t. j. za modeliranje členov \(\hat{S}(p, q)\) in \(\hat{N}(p, q)\).

Naivni pristop za dekonvolucijo, torej 1, je prav tako kot v eni dimenziji izjemno občutljiv na šum; to vidimo v drugem stolpcu na slikah 15, 16 in 17. Poleg naivnega bomo preskusili dva pristopa. Prvi, ki ga poimenujemo W1, bo za fit na spekter "izmerjenega" signala uporabil nastavek \[||C(p, q)|| \sim Ae^{-\Lambda \sqrt{p^2 + q^2}} + C, \quad \text{fit na spekter, pristop \texttt{W1}},\] tako da je prvi eksponenten modelski člen pripadajoč signalu, drugi pa konstantnemu prispevku belega šuma \[\hat{S}(p, q) = Ae^{-\Lambda \sqrt{p^2 + q^2}}, \quad \hat{N} = C.\] V preseku \(p = 0\) vidimo fite na spekter na slikah 13. To modeliranje je precej dobro, a hitro lahko opazimo, da ni optimalno, če si pogledamo spektre signalov na sliki 12, kjer je jasno razvidno, da zaradi oblike konvolucijskega jedra spekter konvolviranega signala ni enako močen v vseh smereh okoli \((p, q) = (0, 0)\), za jedro kernel1 sta na primer razvidna dva zvezdasta kraka, ki izvirata iz spektra konvolucijskega jedra – to jasno vidimo s primerjavo zgornje vrstice na sliki 12 z sredinskim stolpcem na sliki 11. Dodatno potrditev, da je smiselno v nastavek za \(\hat(S)(p, q)\) vnesti spektralno obliko konvolucijskega jedra nam da primerjava sredinske in spodnje vrstice na sliki 12, kjer se jasno vidi, da šum prevlada nad signalom le tam, kjer spekter konvolucijskega jedra nima vrhov. To torej motivira drugi pristop, imenovan W2, pri katerem bomo za fit na spekter uporabili \[||C(p, q)|| \sim A \cdot \| K(p, q) \| \cdot e^{-\Lambda \sqrt{p^2 + q^2}} + C, \quad \text{fit na spekter, pristop \texttt{W2}},\] tako da je zopet prvi modelski člen \(\hat{S}(p, q)\) pripadajoč signalu, drugi \(\hat{N}\) pa konstantnemu prispevku belega šuma. Povsem analogno kot v eni dimenziji lahko iz ocen \(\hat{S}\), \(\hat{N}\) konstruiramo Wienerjev filter \(\Phi(p, q) = \frac{\hat{S}(p,q)^2}{\hat{S}(p,q)^2 + \hat{N}(p,q)^2}\). Konvolvirane in zašumljene slike nato filtriramo (zmnožimo v frekvenčni domeni) z konstruiranim \(\Phi(p, q)\), nato pa delimo z \(K(p, q)\) (še zmerom v frekvenčni domeni). Rezultati takšne dekonvolucije so prikazani na slikah 15, 16 in 17, sicer za naivni pristop ter za pristopa W1 in W2. S primerjavo lahko vidimo, da je pristop W2 nekoliko boljši, predvsem je prisotnih manj banding artefaktov (glej npr. sliko 16, druga in tretja vrstica). Na inset slikicah slik 15, 16 in 17 je prikazana oblika \(\Phi(p, q)\). Kot namigujejo inset slikice, je pristop W2 boljši, ker spektralne komponente maskira bolj selektivno – le tam, kjer je konvolucija za izbrano jedro spektralne komponente zmanjšala pod prag šuma.

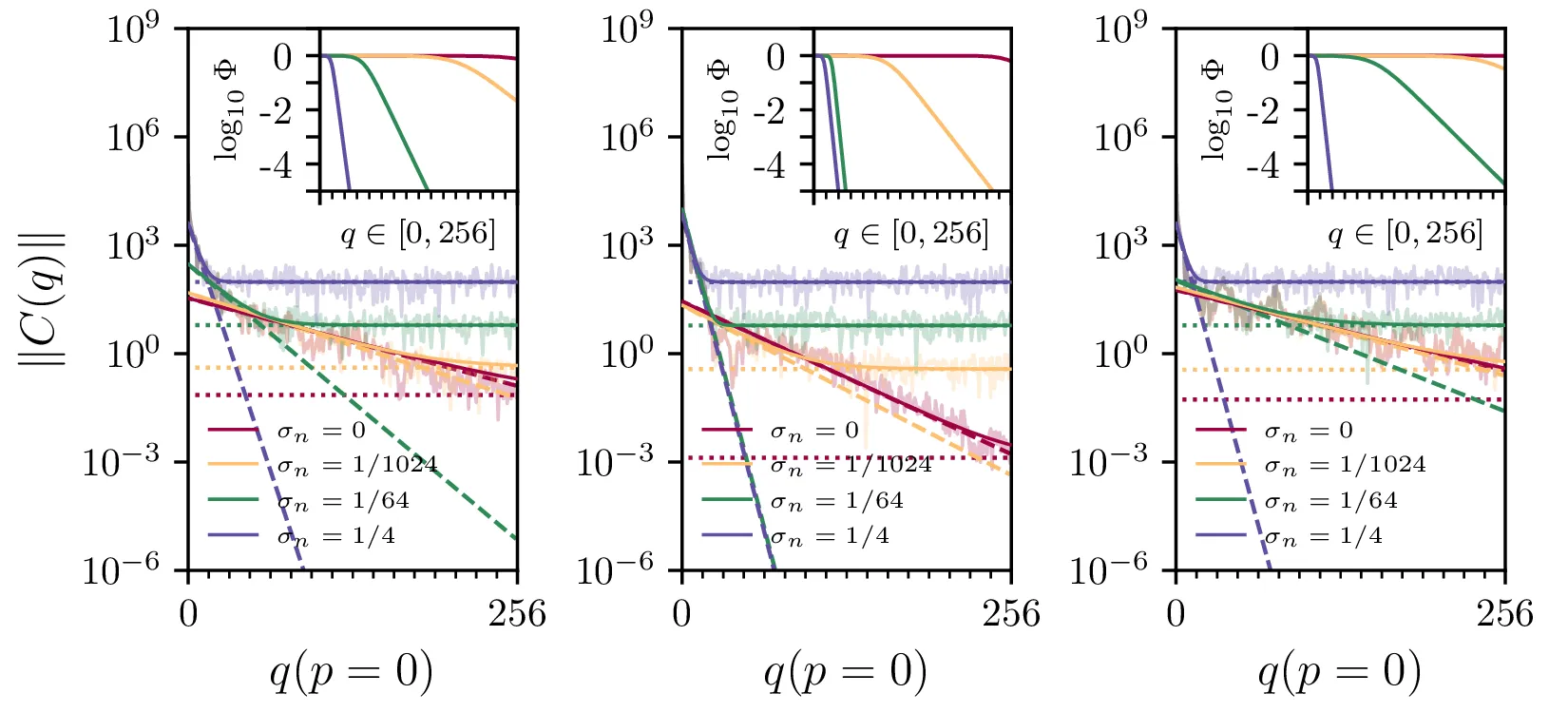
Pristop `W1`. Spektri signalov \(c(i,j)\), za konvolucijska jedra `kernel{1,2,3}`, od leve proti desni. Različne barve označujejo amplitude dodanega šuma. Na spekter smo prilagodili model \(C(p, q) = A e^{-\Lambda\sqrt{p^2 + q^2}} + C\), sestavljen iz člena za signal \(\hat{S} = A e^{-\Lambda\sqrt{p^2 + q^2}}\) (za različne \(\sigma_n\) narisan kot črtkane premice) in konstantnega člena šuma \(\hat{N} = C\) (narisan kot pikčaste vodoravne premice). Desno zgoraj je za vsak spekter narisan Wienerjev filter \(\Phi(p, q) = \frac{\hat{S}(p,q)^2}{\hat{S}(p,q)^2 + \hat{N}(p,q)^2}\), ki ga skonstruiramo iz ocen \(\hat{S}\) in \(\hat{N}\).

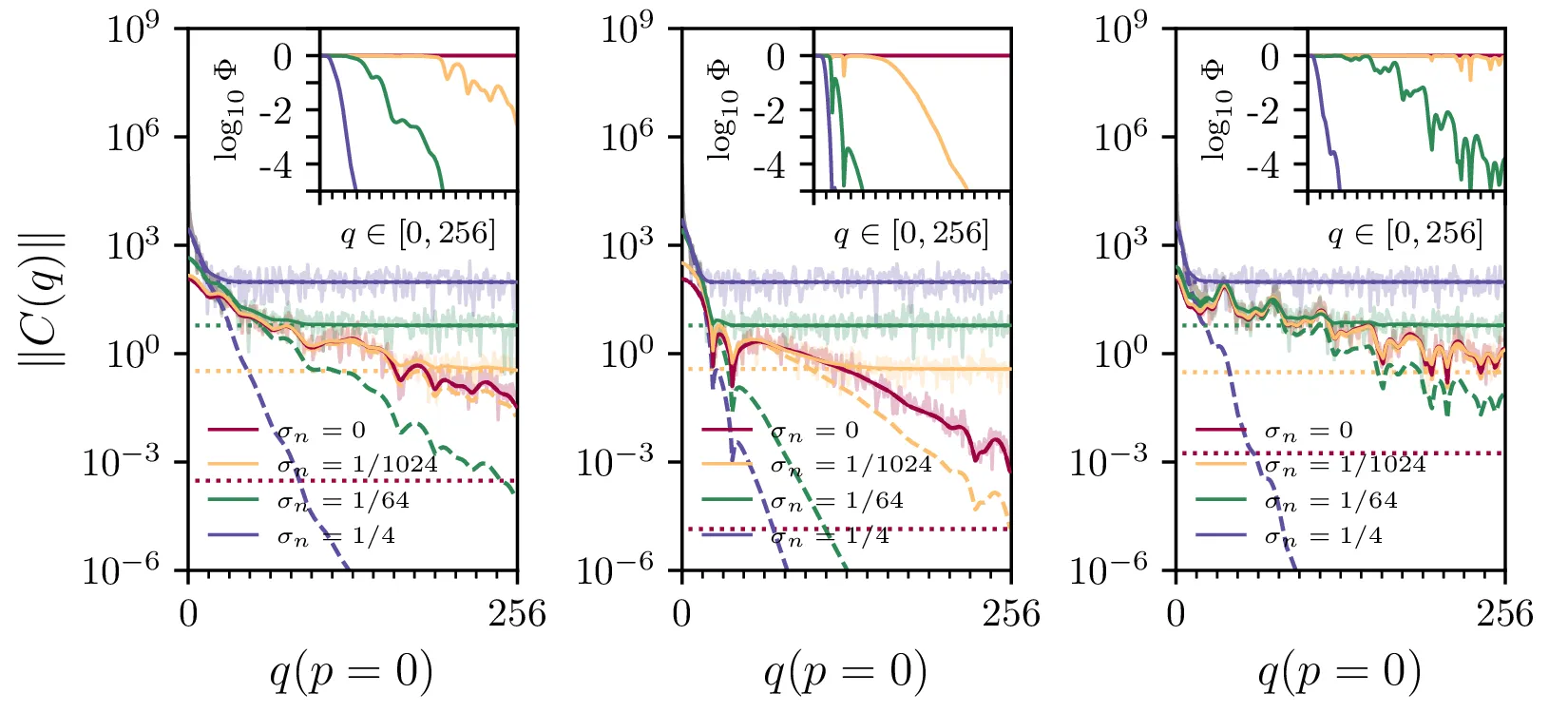
Pristop `W2`. Spektri signalov \(c(i,j)\), za konvolucijska jedra `kernel{1,2,3}`, od leve proti desni. Različne barve označujejo amplitude dodanega šuma. Na spekter smo prilagodili model \(C(p, q) = A \cdot \| K(p, q) \| \cdot e^{-\Lambda\sqrt{p^2 + q^2}} + C\), sestavljen iz člena za signal \(\hat{S} = A \cdot \| K(p, q) \| \cdot e^{-\Lambda\sqrt{p^2 + q^2}}\) (za različne \(\sigma_n\) narisan kot črtkane krivulje) in konstantnega člena šuma \(\hat{N} = C\) (narisan kot pikčaste vodoravne premice). Desno zgoraj je za vsak spekter narisan Wienerjev filter \(\Phi(p, q) = \frac{\hat{S}(p,q)^2}{\hat{S}(p,q)^2 + \hat{N}(p,q)^2}\), ki ga skonstruiramo iz ocen \(\hat{S}\) in \(\hat{N}\).

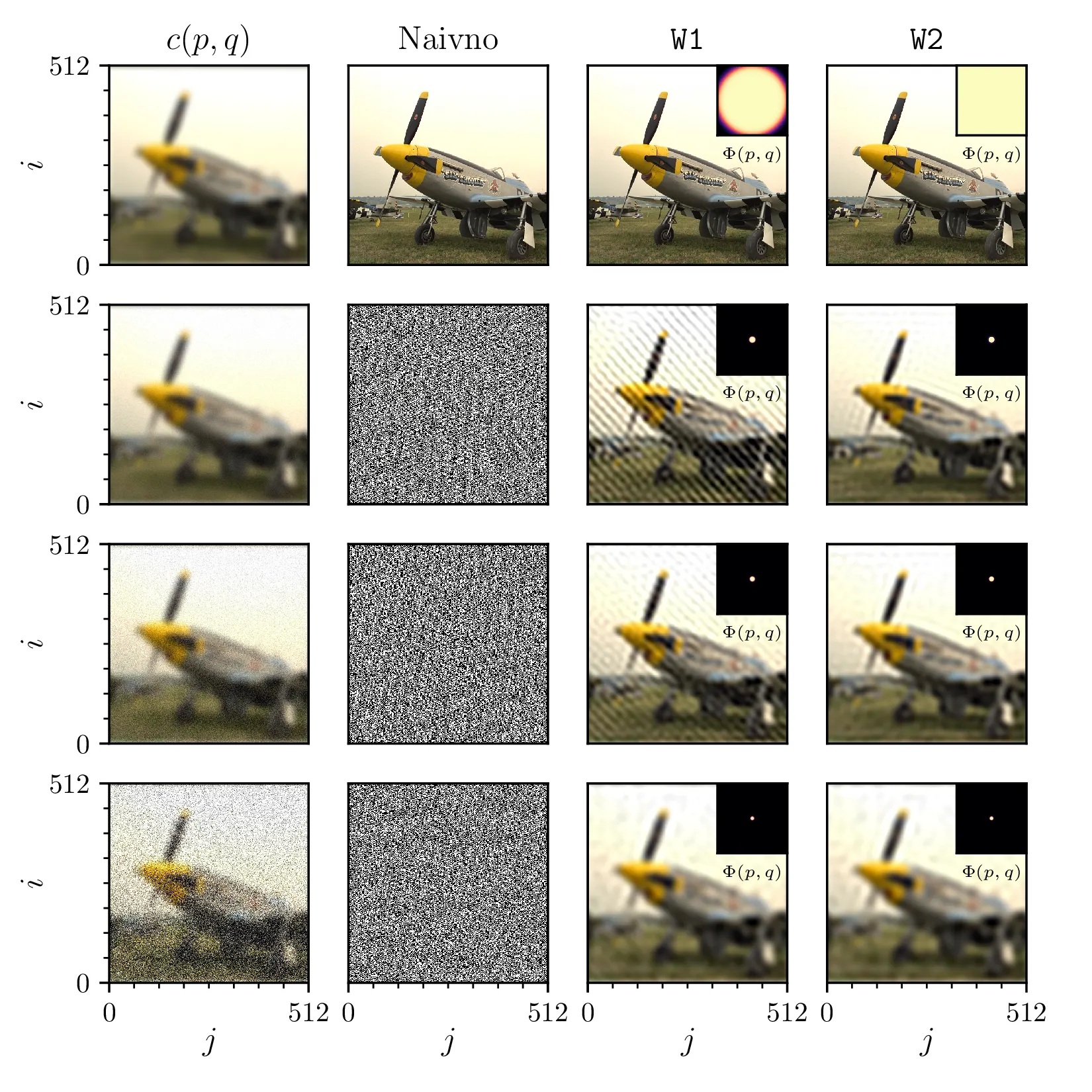
Rekonstrukcije iz konvolvirane in zašumljene slike, z jedrom `kernel1`. Amplitude šuma od zgoraj navzdol \(\sigma_n = \{ 0, 1/64, 1/16, 1/4\}\). Prikazani so tri različni načini rekonstrukcije oz. dekonvolucije. Prvi je naivni pristop, ki dobro deluje, ko ni prisotnega šuma (zgornja vrstica, \(\sigma_n = 0\), a zelo hitro degradira že z majhnim dodanim šumom). Za pristop `W1` uporabimo Wienerjev filter, s preprostim eksponentnim nastavkom za člen \(\hat{S}(p, q)\) (glej sliko 13). Nekoliko kompleksnejši pristop `W2` uporabi za nastavek \(\hat{S}(p, q)\) še znano obliko spektra \(\| K(p, q) \|\), kar omogoči, da je Wienerjev filter bolj selektiven in maskira le tiste regije, kjer je spekter po konvoluciji šibkejši od šuma; to izboljša rekonstrukcijo pri zmerni amplitudi šuma, saj ohrani pomembne spektralne komponente, ki bi jih `W1` zamaskiral.

Rekonstrukcije iz konvolvirane in zašumljene slike, z jedrom `kernel2`. Amplitude šuma od zgoraj navzdol \(\sigma_n = \{ 0, 1/64, 1/16, 1/4\}\). Prikazani so tri različni načini rekonstrukcije oz. dekonvolucije. Glej opis slike 15.

Rekonstrukcije iz konvolvirane in zašumljene slike, z jedrom `kernel3`. Amplitude šuma od zgoraj navzdol \(\sigma_n = \{ 0, 1/64, 1/16, 1/4\}\). Prikazani so tri različni načini rekonstrukcije oz. dekonvolucije. Glej opis slike 15.

Viri

[1]

J. H. Hubbard in B. H. West, Differential Equations: A Dynamical Systems Approach: Ordinary Differential Equations. New York: Springer, 1991.

[2]

S. P. N. Ernst Hairer Gerhard Wanner, Solving Ordinary Differential Equations: Nonstiff Problems, 2. izd., let. 2. v Springer Series in Computational Mathematics 8, vol. 2. Springer-Verlag Berlin Heidelberg, 1993.