Modelska analiza I
9. naloga: Stohastični populacijski modeli
Navodila
-
Napravi statistiko časov izumrtja za preprosti eksponentni model (\(\beta = 1.0/\text{enota časa}\)) za majhno (\(N = 25\)) in veliko (\(N = 250\)) populacijo. Ali je ta čas odvisen od velikosti časovnega koraka? Primerjaj z modelom, ki vključuje rojstva in smrti (\(\beta_r = 4\beta\), \(\beta_s = 5\beta\))!
-
Za zgornji model poišči matriko prehodov in z njo oceni čas izumrtja. Za preprost eksponentni model izumiranja lahko zapišeš enačbe za verjetnostno porazdelitev v odvisnosti od časa. Kako se efektivni odmik te porazdelitve spreminja s časom?
-
V stohastičnem modelu zajci-lisice določi povprečno življenjsko dobo sistema, če začnemo v ravnovesnem stanju. Za boljšo primerjavo med rezultati uporabi stacionarno stanje z 200 zajci in 50 lisicami in razmerje rodnost/smrtnost \(5/4\) za zajce in obratno za lisice.
-
Stohastično simuliraj model epidemije iz 4. naloge z dodano možnostjo, da imuni postopoma spet postajajo dovzetni. Kakšna je statistika časov popolne eliminacije bolezni v odvisnosti od velikosti populacije in hitrosti izgubljanja imunosti?
Model izumrtja
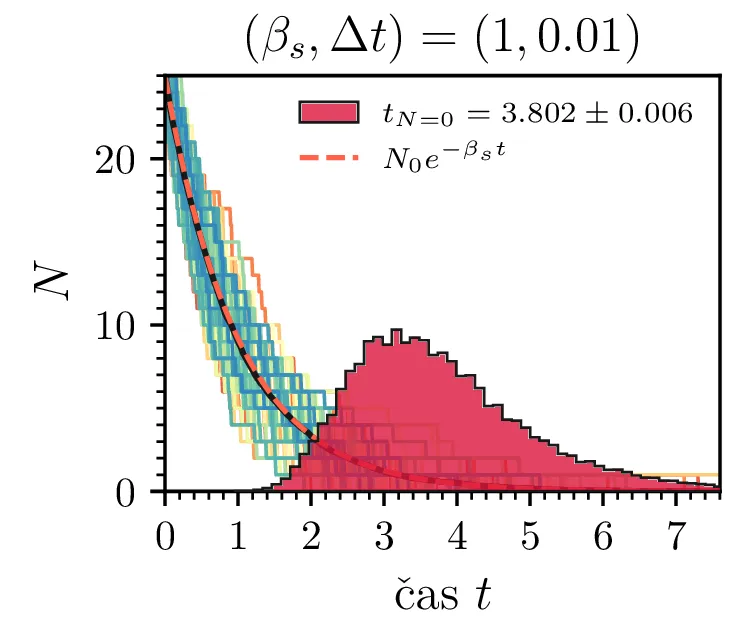
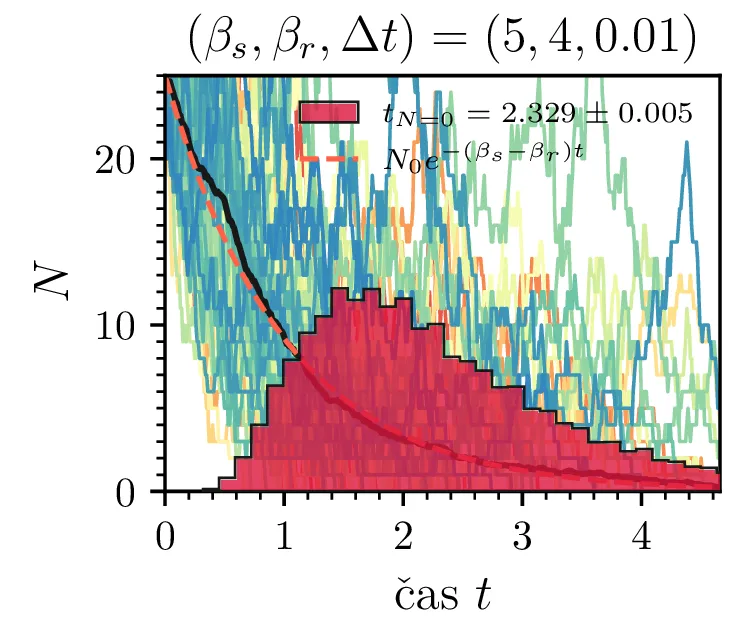
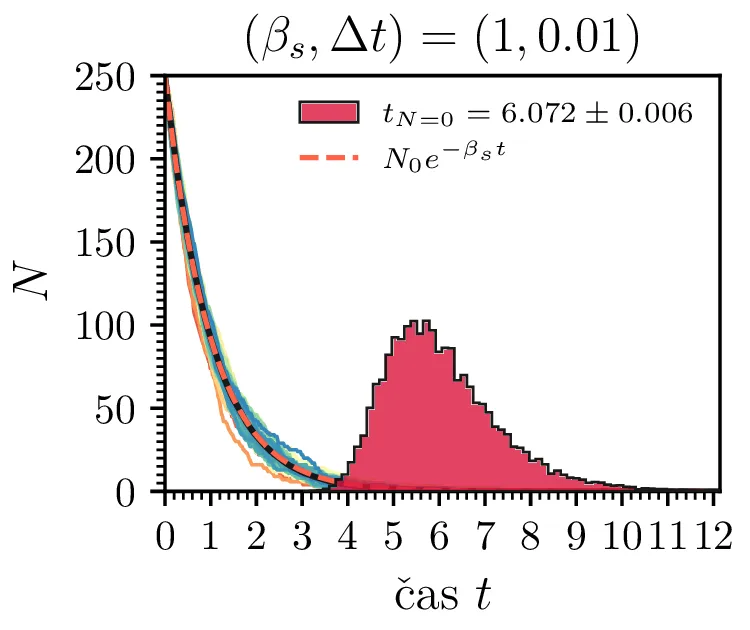
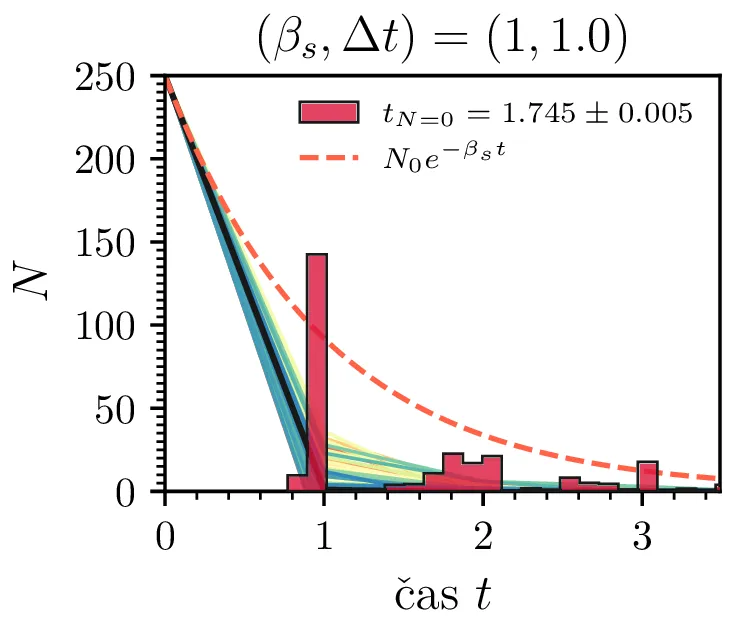
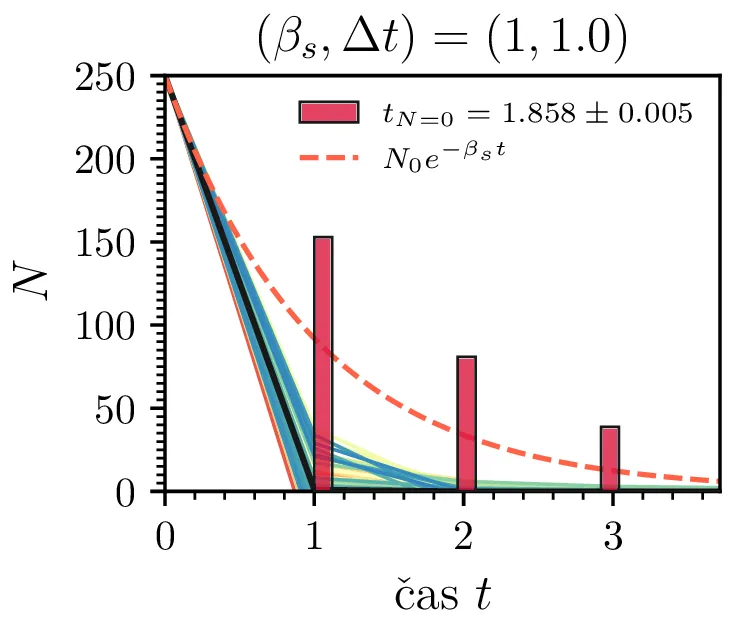
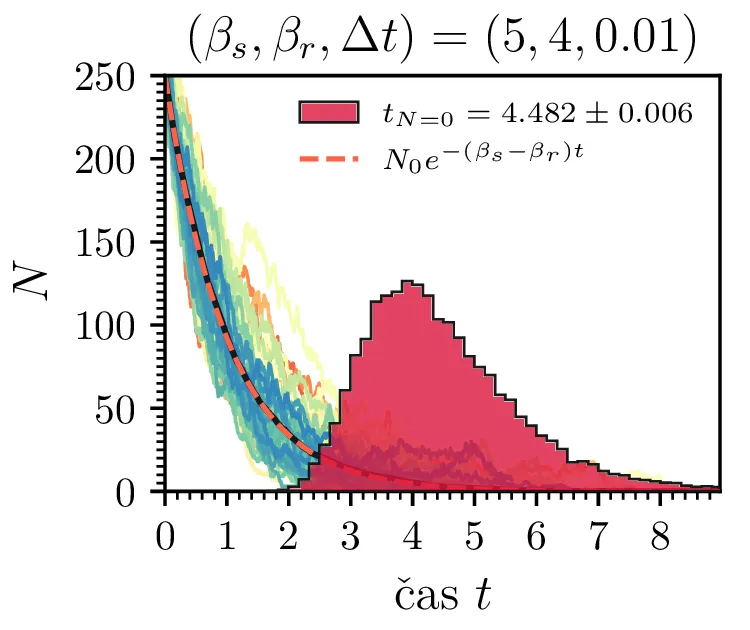
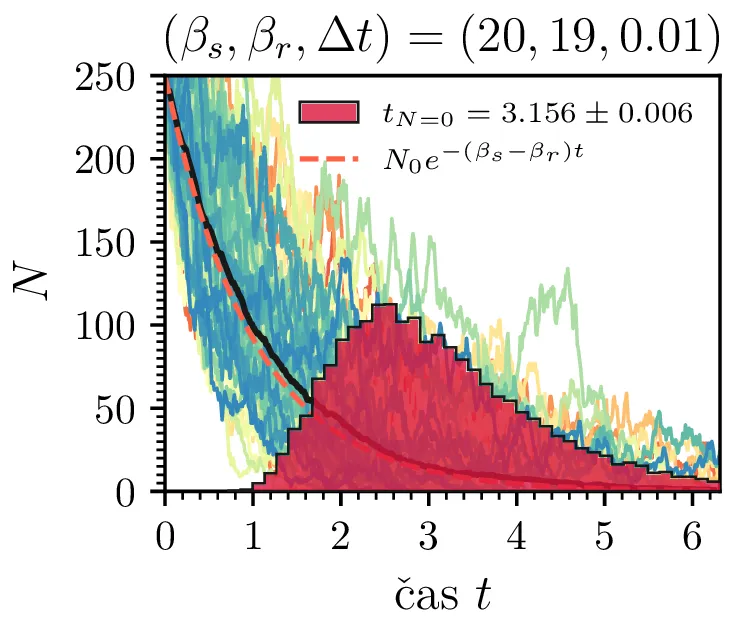
Prvo si pogledamo preprost model izumrtja, pri katerem začetno populacijo \(N(t = 0) = N_0\) zmanjšujemo stohastično kot \[N(t + \Delta t) = N(t) - \mathcal{P}(\beta_s N \Delta t),\] pri čemer je \(\mathcal{P}(\lambda)\) naključno število žrebano iz Poissonove porazdelite s povprečjem \(\lambda\). Povprečje \(\lambda = \beta N \Delta t\) je v osnovi eksponentno, tako da je \(\dot{N} \propto N\). V model izumiranja lahko dodamo še pojav rojstev, z dodatnim stohastičnim členom \begin{equation}N(t + \Delta t) = N(t) - \mathcal{P}(\beta_s N \Delta t) + \mathcal{P}(\beta_r N \Delta t). \label{eq:stohastic-de}\end{equation} V zvezni sliki ne-stohastične diferencialne enačbe bi to pomenilo rešitev združenih eksponentov \(N(t) = N_0 e^{-(\beta_s - \beta_r) t}\). A v stohastični sliki ima to dodatno posledico v tem, da porazdelitev časov izumrtja razširi. To lahko vidimo na sliki 1 kjer primerjamo med modelom izumrtja in modelom izumrtja z rojstvi, za začetno populacijo \(N_0 = 25\). To lahko razširimo tudi na primera \((\beta_s, \beta_r) = (5, 4)\) in \((20, 19)\) za večjo začetno populacijo na sliki 3.
Vpliv časovnega koraka
Da je simulacija statistično pravilna, mora biti korak \(\Delta t\) zadostno majhen, drugače umetno omejimo število možnih prehodov iz \(N > 0\) v \(N \le 0\). Najbolje to vidimo na slikah 2 sredinsko in desno, kjer je korak \(\Delta t = 1\). Vidimo, da histogram razpade na tri ločene vrhove, ki jih določa celoštevilski naklon možnih Poissonovskih skokov v prostoru \((t, N(t))\). Edina razlika med sredinsko in desno sliko je uporaba interpolacijske sheme, kjer čas izumrtja razumemo kot presečišče daljice med \((t_1, N_1)\) in \((t_2, N_2)\), pri čemer je \(N_1\) zadnji \(N > 0\), drugi \(N_2\) pa je prvi \(N \le 0\). Tako interpolacijsko shemo uporabljamo povsod v nadaljevanju, kjer je to smiselno.
Odvisnost časov izumrtja od parametrov
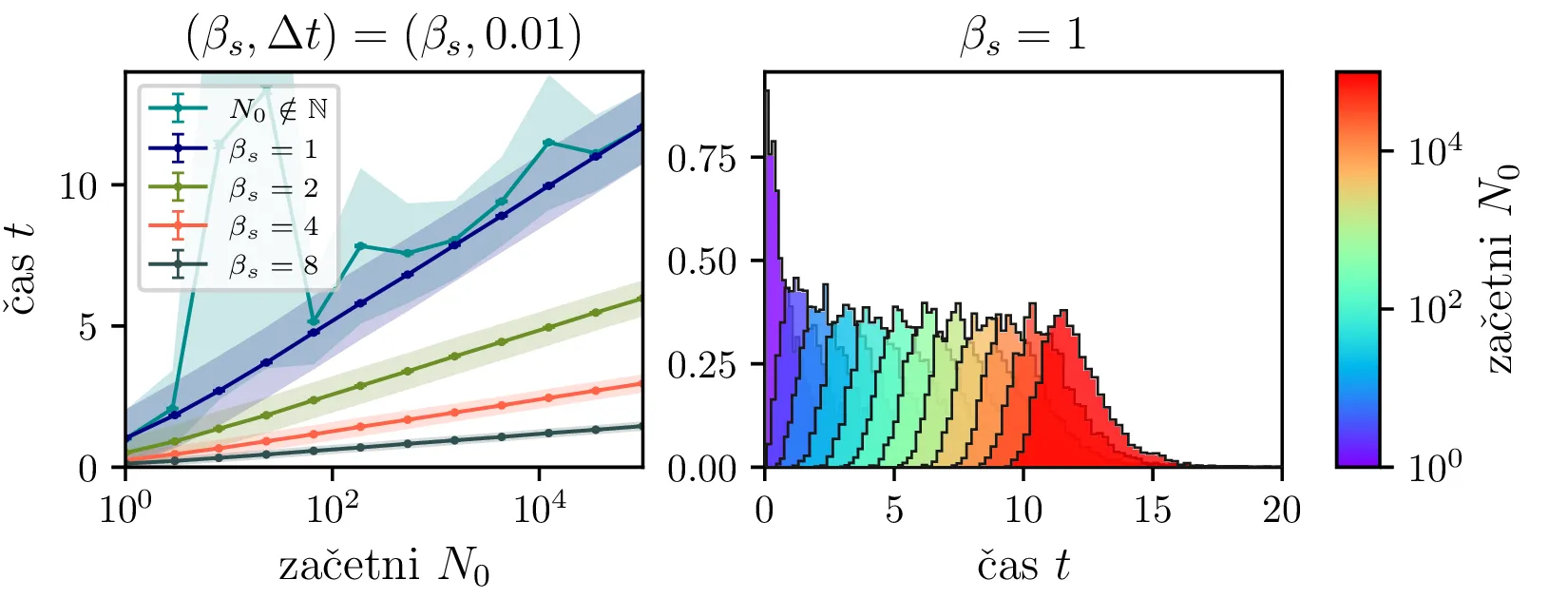
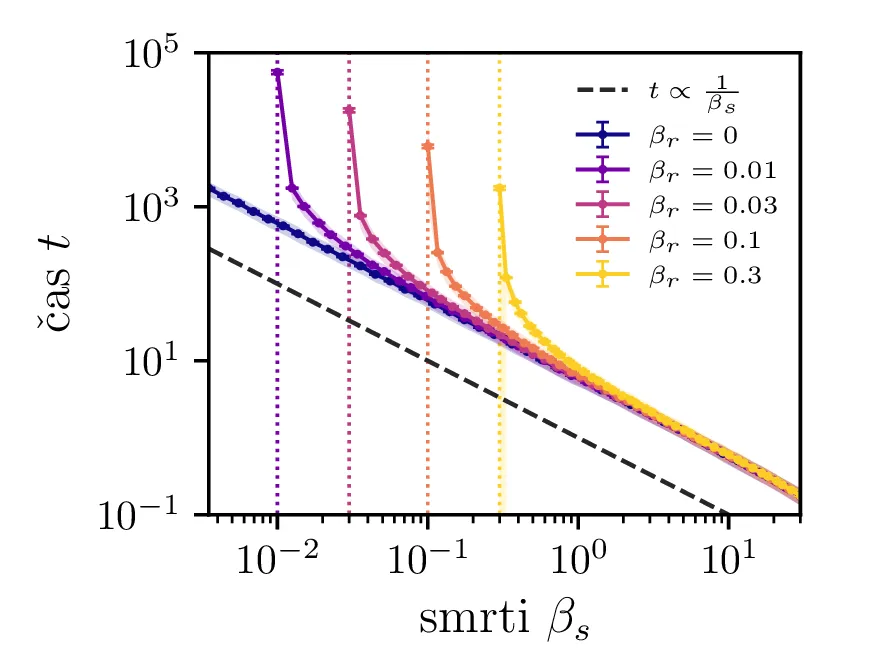
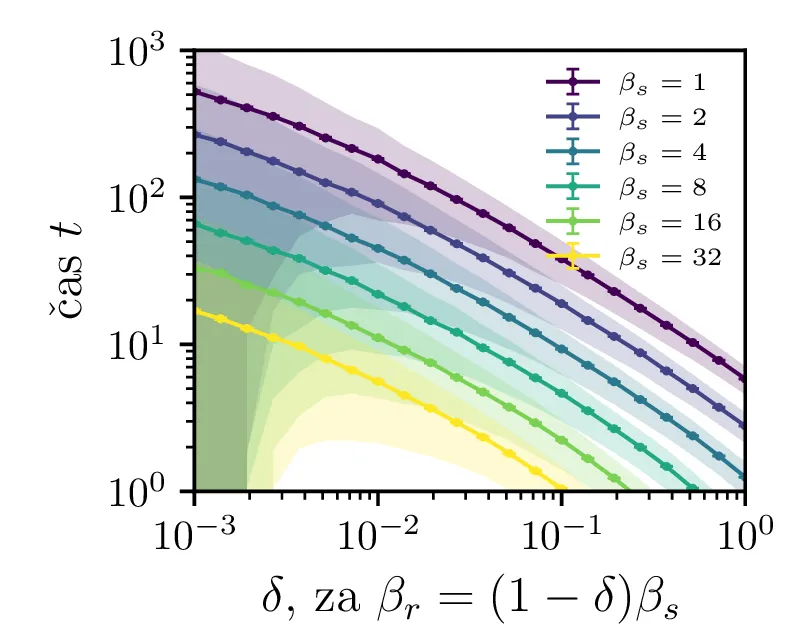
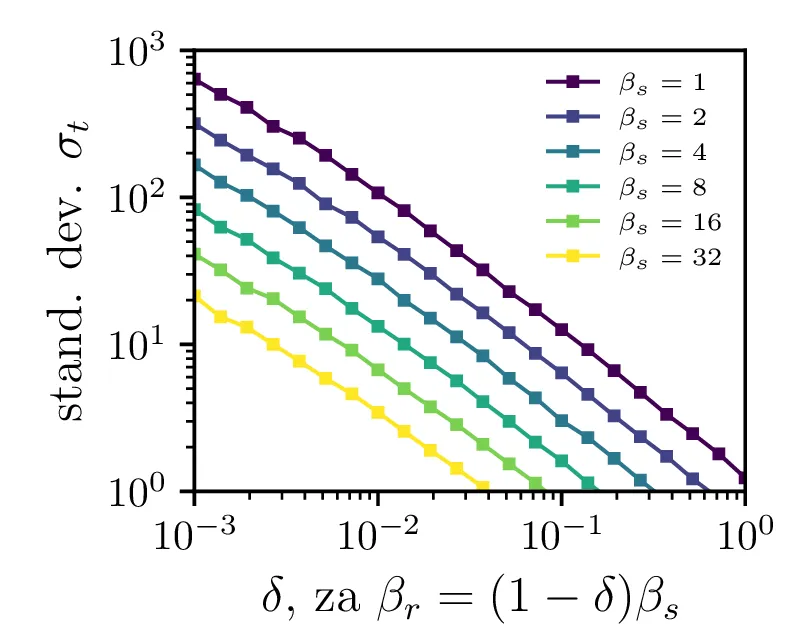
Na sliki 4 v log-linearni skali vidimo kako povprečen čas potreben za izumrtje logaritemsko narašča z velikostjo začetne populacije. Vidim lahko tudi napačen način računanja, kjer za \(N_0\) vzamemo necelo število, to pa povzroči statistično povsem nesmiselne rezultate, kjer se populacij zatakne pri nekem majhnem realnem številu \(N \in (0, 1)\). Poleg začetne velikosti populacije na povprečen čas izumrtja vpliva tudi hitrost izumiranje \(\beta_s\). Kot vidimo na sliki 5, je za \(\beta_s \ll \beta_r\) ta odvisnost smiselna in intuitivna \(t \propto \frac{1}{\beta_s}\). A za \(\beta_r \approx \beta_s\) ta čas močno naraste, saj je obnašanje bolj difuzivno, poleg smrti, ki premikajo \(N\) navzdol, so prisotna tudi rojstva, ki premikajo \(N\) navzgor. Bolj podroben pogled na te pole, kjer čas in njegova varianca narasteta, vidimo na sliki 6.
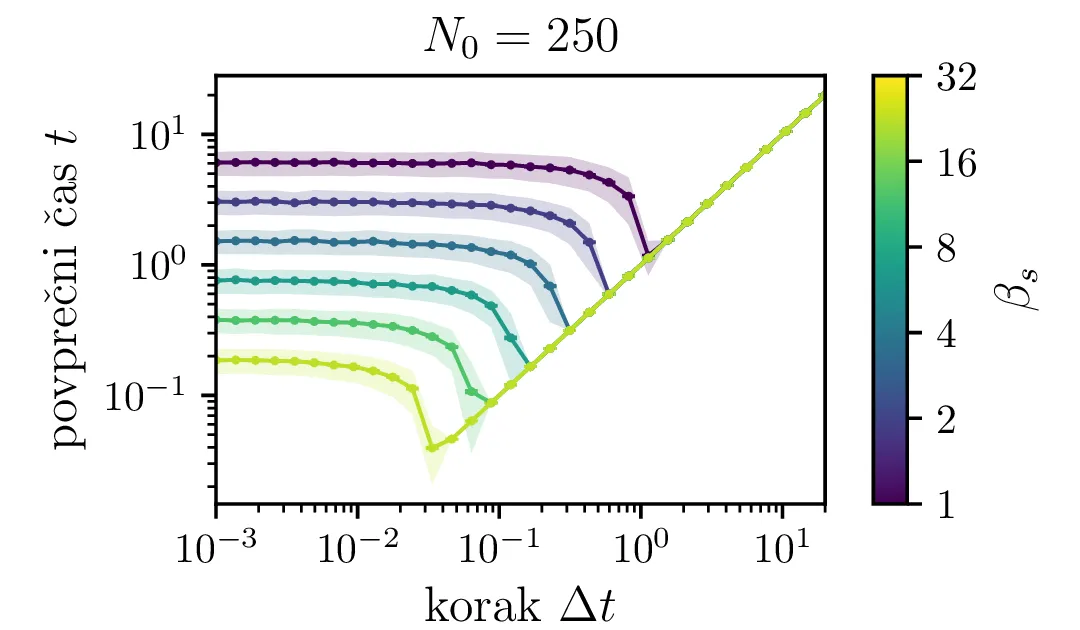
Na sliki 7 je narisana odvisnost povprečnih časov za neko izbiro hitrosti procesa \(\beta_s\) od koraka stohastične integracije. Kot pričakovano je potrebna za smiseln rezultat dovolj velika resolucija, t. j. dovolj majhen \(\Delta t\). Za večje \(\beta_s\) je tipično potrebna izbira manjšega koraka.
Model prehodne matrike
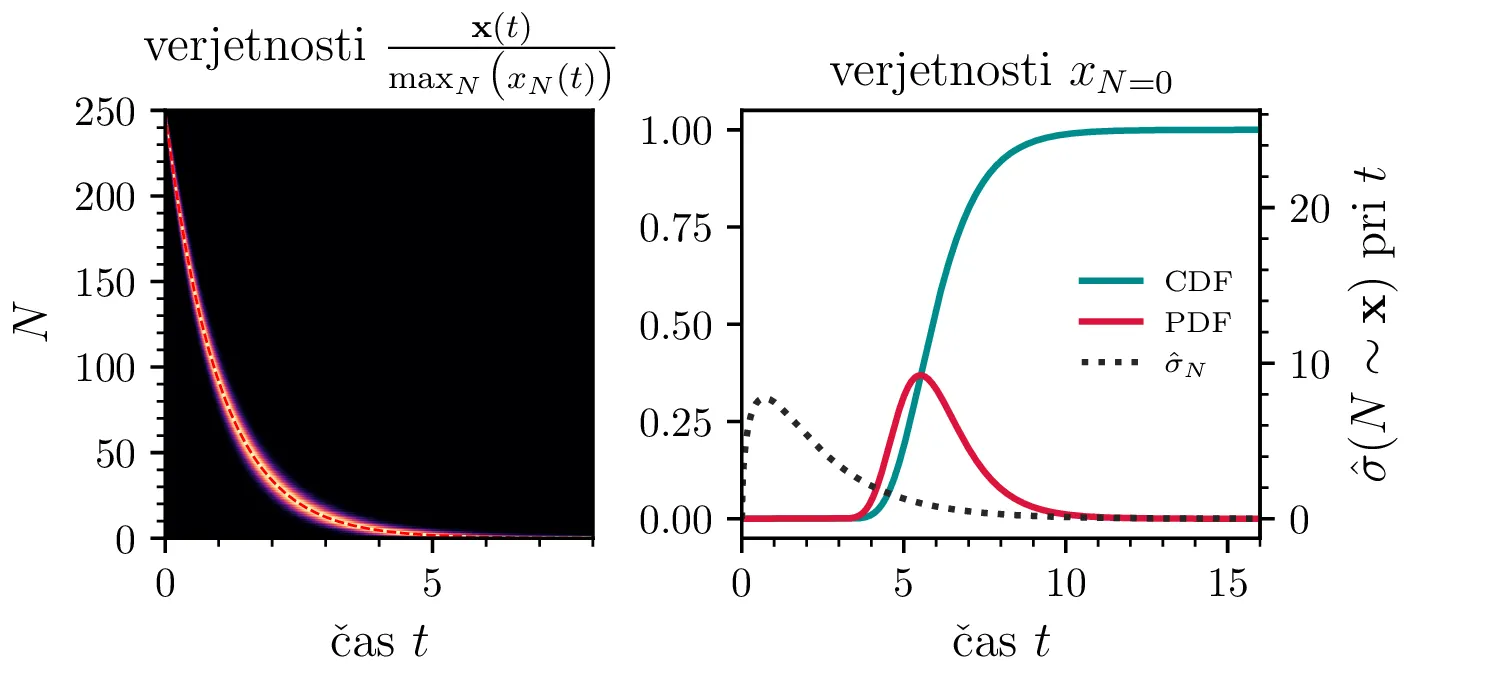
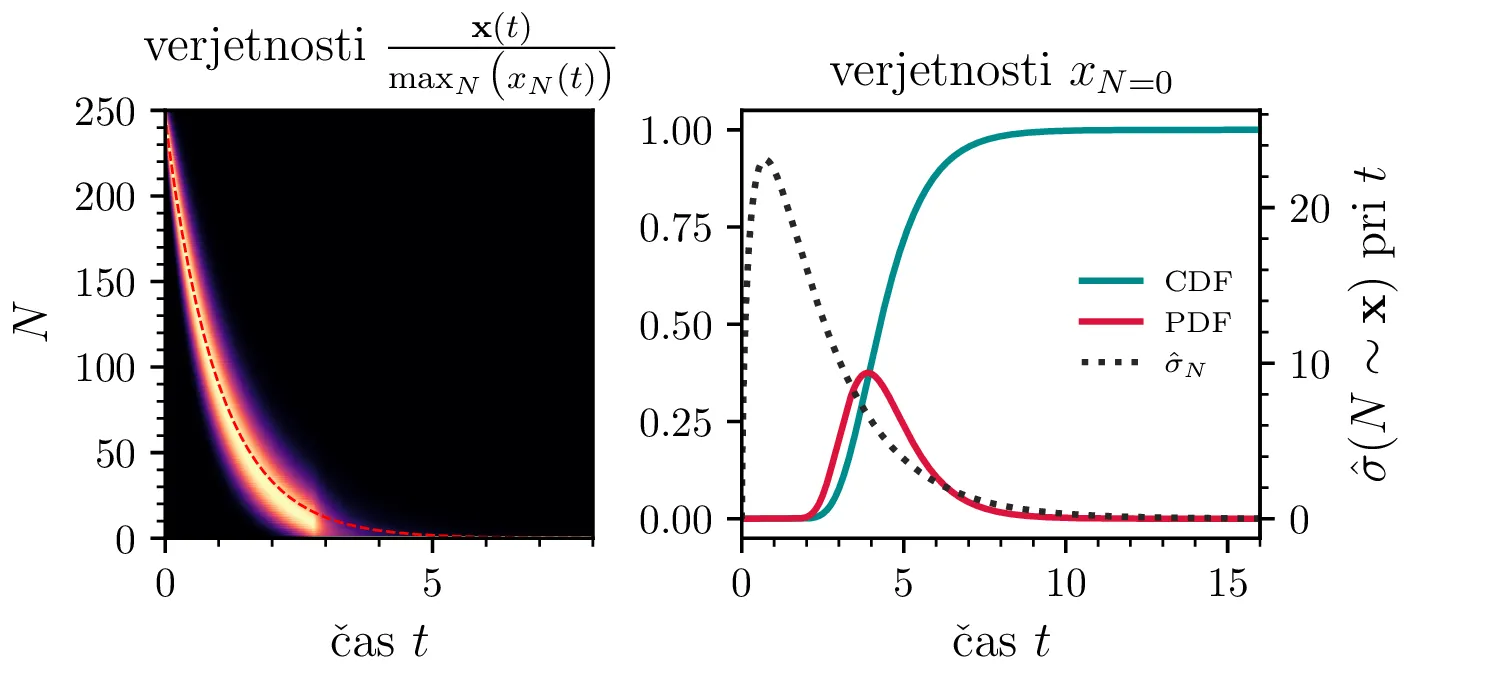
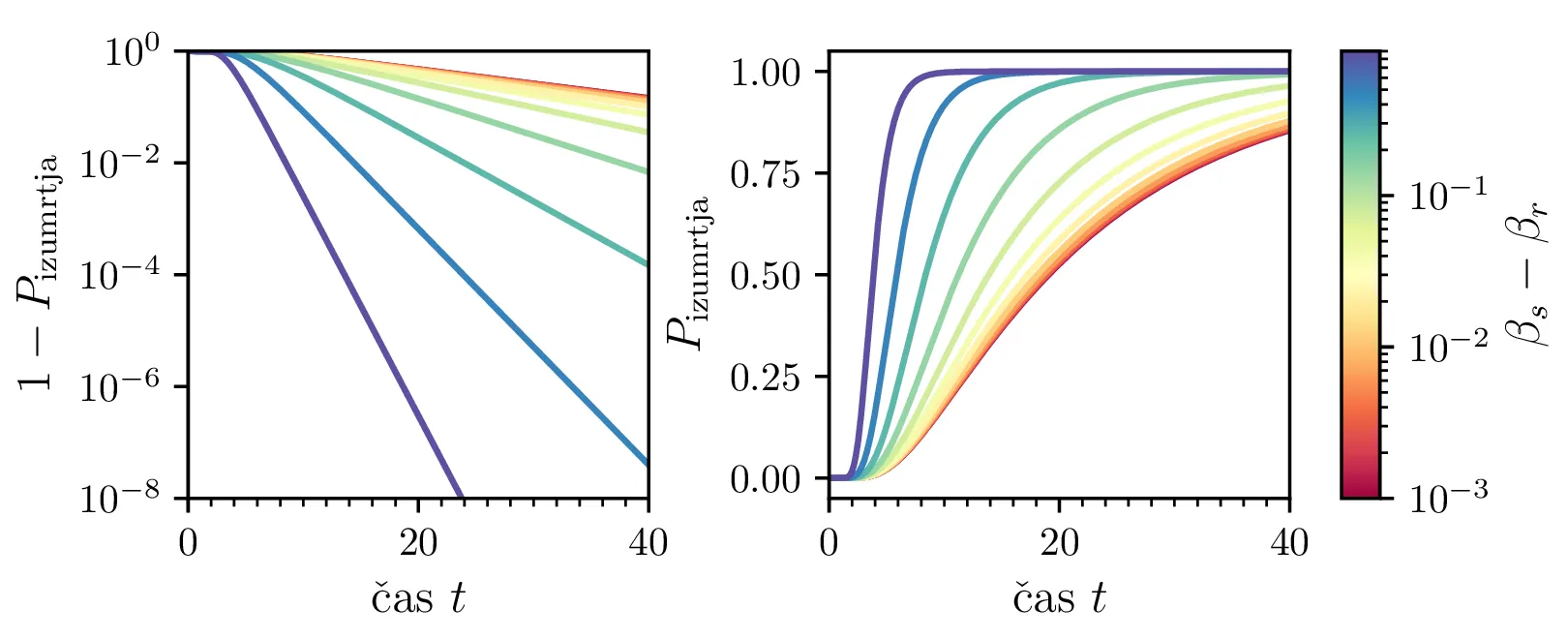
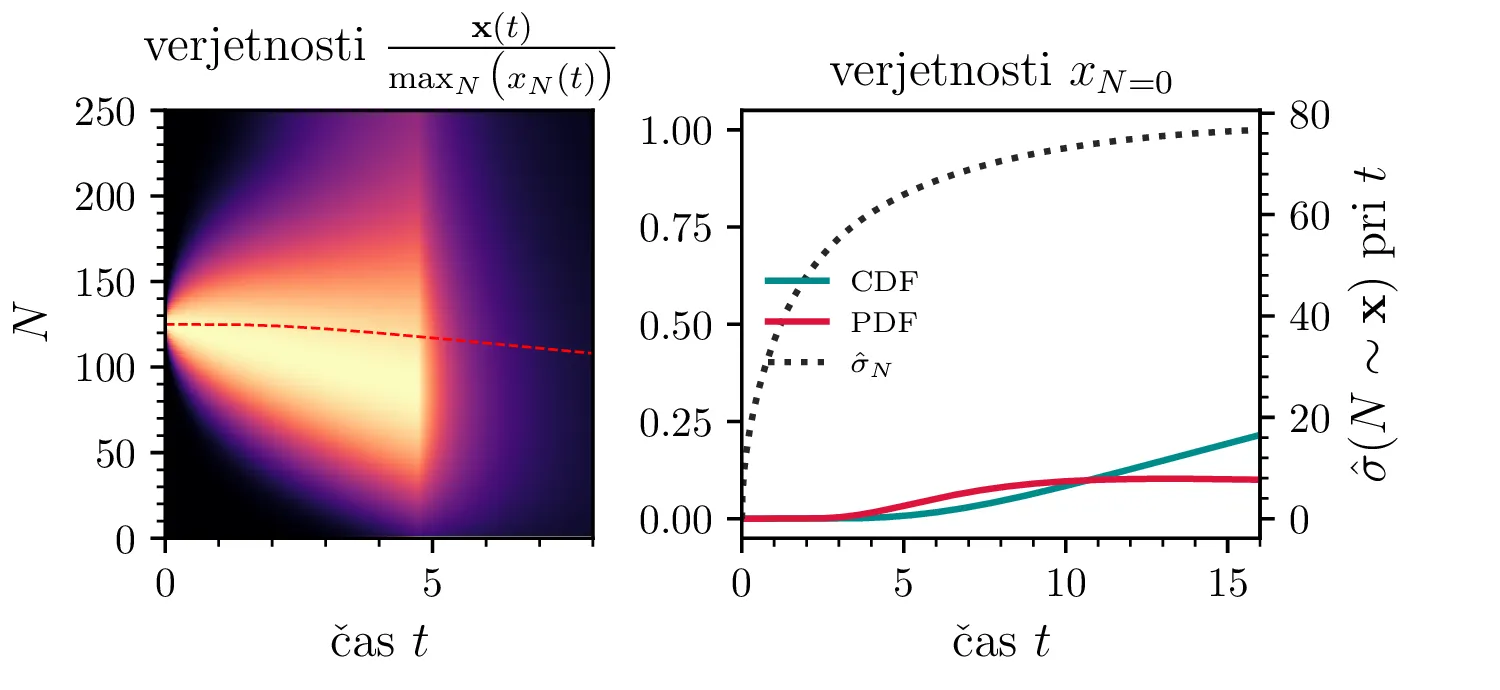
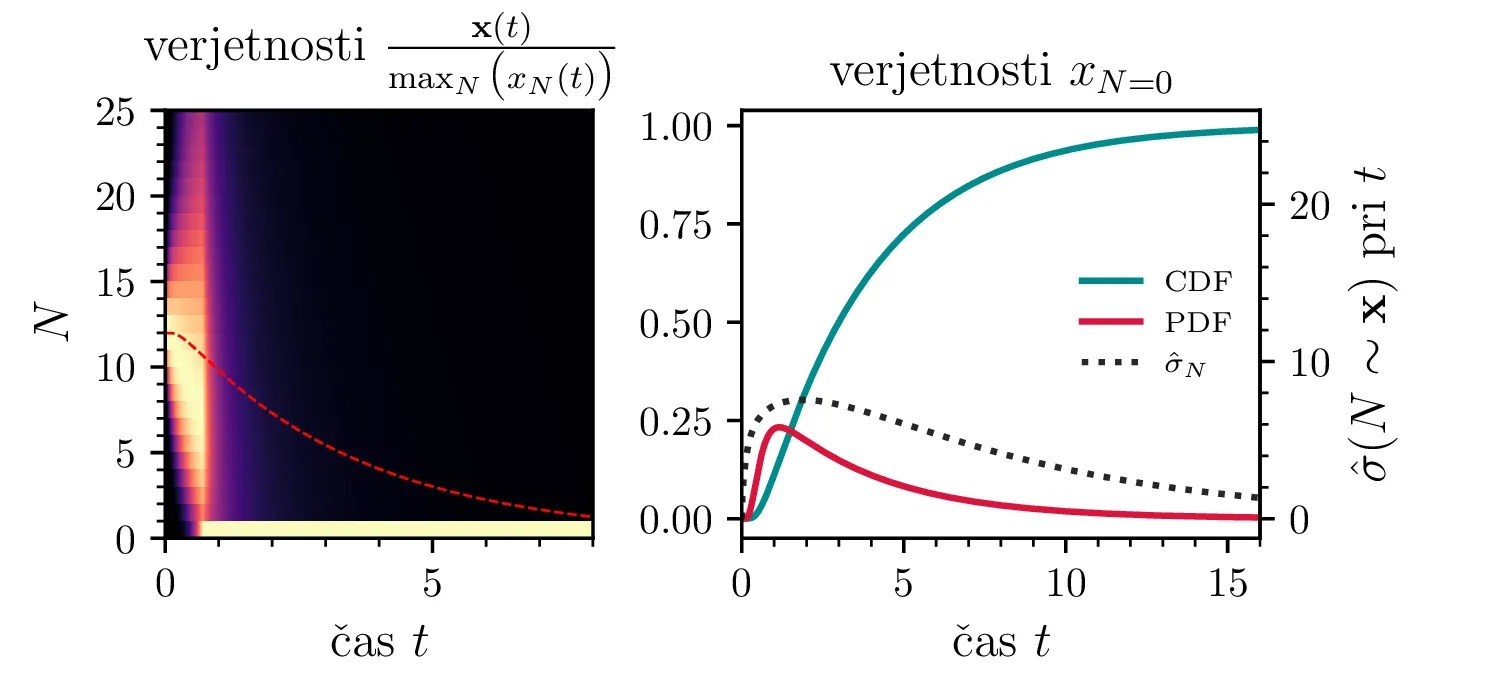
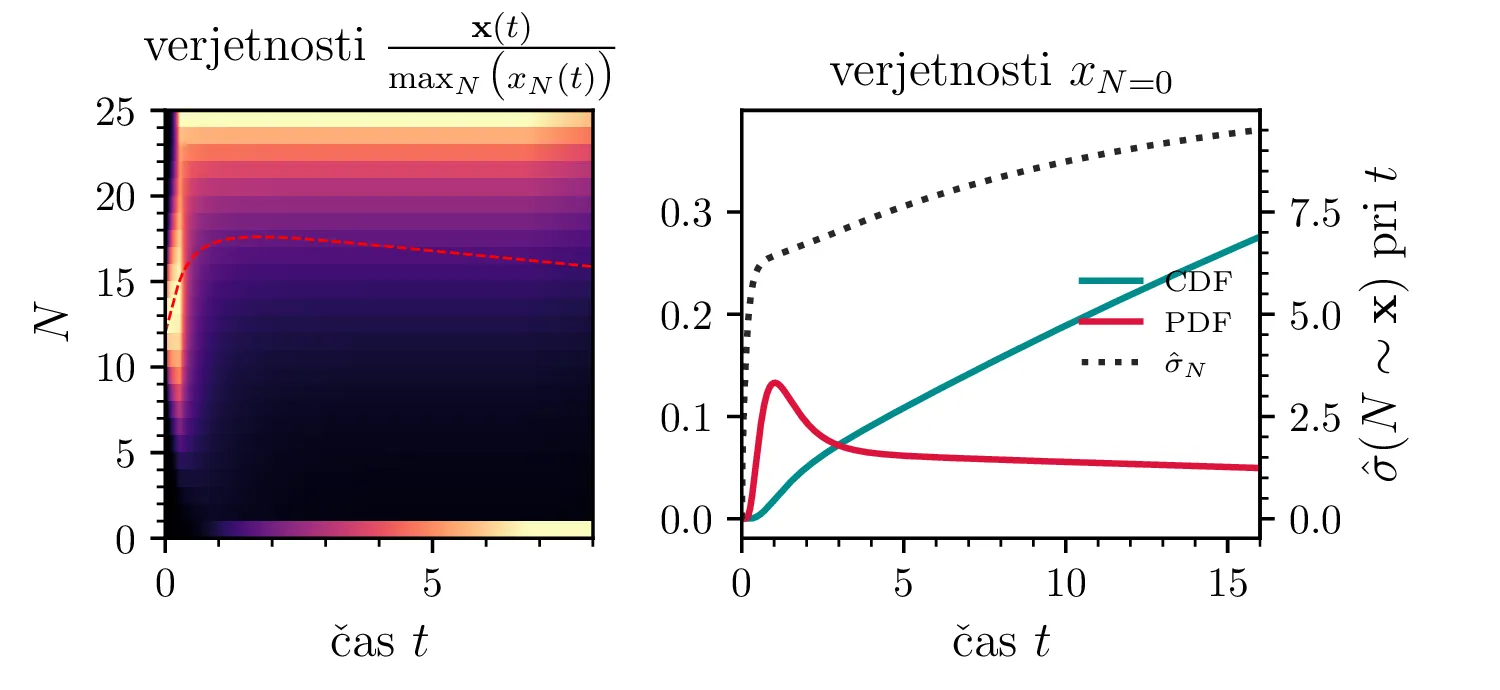
Namesto ansambla žrebanih rešitev stohastične diferencialne enačbe 1 lahko problem prevedemo na stohastični proces, konkretno Markovsko verigo, ki opisuje evolucijo porazdelitvenega vektorja. Primer takega vektorja za populacijo \(0 \ge N \ge N_0\) in \(N_0 = 9\) je zapisan kot \[\mathrm{x}_9 = \begin{pmatrix} p_{N = 0} & p_{N = 1} & \hdots & p_{N = 8} & p_{N = 9} \end{pmatrix}^T.\] Če nas zanima evolucija porazdelitev za populacijo \(N(t = 0) = N_0\), je začetna porazdelitev pri času \(t = 0\) oblike \[\mathrm{x}_9(t = 0) = \begin{pmatrix} 0 & 0 & \dots & 0 & 1 \end{pmatrix}^T.\] Za čase \(t > 0\) lahko porazdelitev razvijemo kot matrično množenje \[\mathbf{x}(t + h) = M \mathbf{x}(t),\] pri čemer je Markovska matrika, t. i. prehodna matrika oblike \[M_9 = \begin{pNiceMatrix} 1 & S h \\ 0 & 1 - 1(B + S) & 2S \\ & B & 1 - 2(B + S) & 3S \\ & & \Ddots & \Ddots & \Ddots \\ & & & 7 B & 1 - 8(B + S) & 9 S \\ & & & & 8 B & 1 - 9 S \end{pNiceMatrix},\] pri čemer sta \(B\) in \(S\) le okrajšavi za \[B \vcentcolon=\beta_s \Delta t, \quad S \vcentcolon=\beta_r \Delta t.\] Na sliki 8 zgoraj vidimo evolucijo porazdelitve pri zaporednih množenjih z matriko za \(\beta_s = 1\). Začetna porazdelitev z ničelno varianco se razširi, nato pa počasi premakne proti stacionarni porazdelitvi \(\mathbf{x} = (1, 0, \dots, 0, 0)\), ki pomeni izumrtje populacije. Na sliki 8 desno zgoraj vidimo tudi odvisnost \(\sigma_N\) od časa, v rdeči in modri barvi pa tudi CDF in PDF verjetnosti za izumrtje. Prav tako kot smo to ugotovili za stohastično diferencialno enačbo 1 se ob dodatku \(\beta_r > 0\) verjetne trajektorije razširijo (slika 8 spodaj). Kako točno \(\beta_r > 0\) vpliva na potek izumiranja, najlepše vidimo na sliki 9, kjer rišemo kumulativno verjetnost izumrtja po času za \(\beta_s = 1\) in malo manjši \(\beta_r = \beta_s - \varepsilon < 1\).
Difuzivni režim
V analogu ne-stohastične diferencialne enačbe je izumiranje prisotno le v režimu \(\beta_s > \beta_r\). A možna stanja diskretiziranega populacijskega modela z Markovsko verigo so navzgor omejena \(M \le N_0\), stanje izumrtja \(\mathbf{x} = (1, 0, \dots, 0, 0)\) pa je edino stacionarno stanje procesa. Tako je pojav izumrtja prisoten tudi za \(\beta_s \ge \beta_r\). To vidimo v različnih realizacijah na sliki 10, kjer vidimo difuzivni režim \(\beta_s = \beta_r\) za začetno populacijo \(N_0 = 250\). Vidimo tudi difuzijo iz začetnega stanja \(N(t = 0) = N_0 / 2\) za \(N_0 = 25\), kjer se trajektorije sprva širijo enakomerno gor in dol (rojstva in smrti), na koncu pa se vseeno ustalijo v stanju izumrtja. Nekoliko presenetljivo velja tudi za režim \(\beta_r > \beta_s\) (slika 10 spodaj).
Stohastični Lotka-Volterra
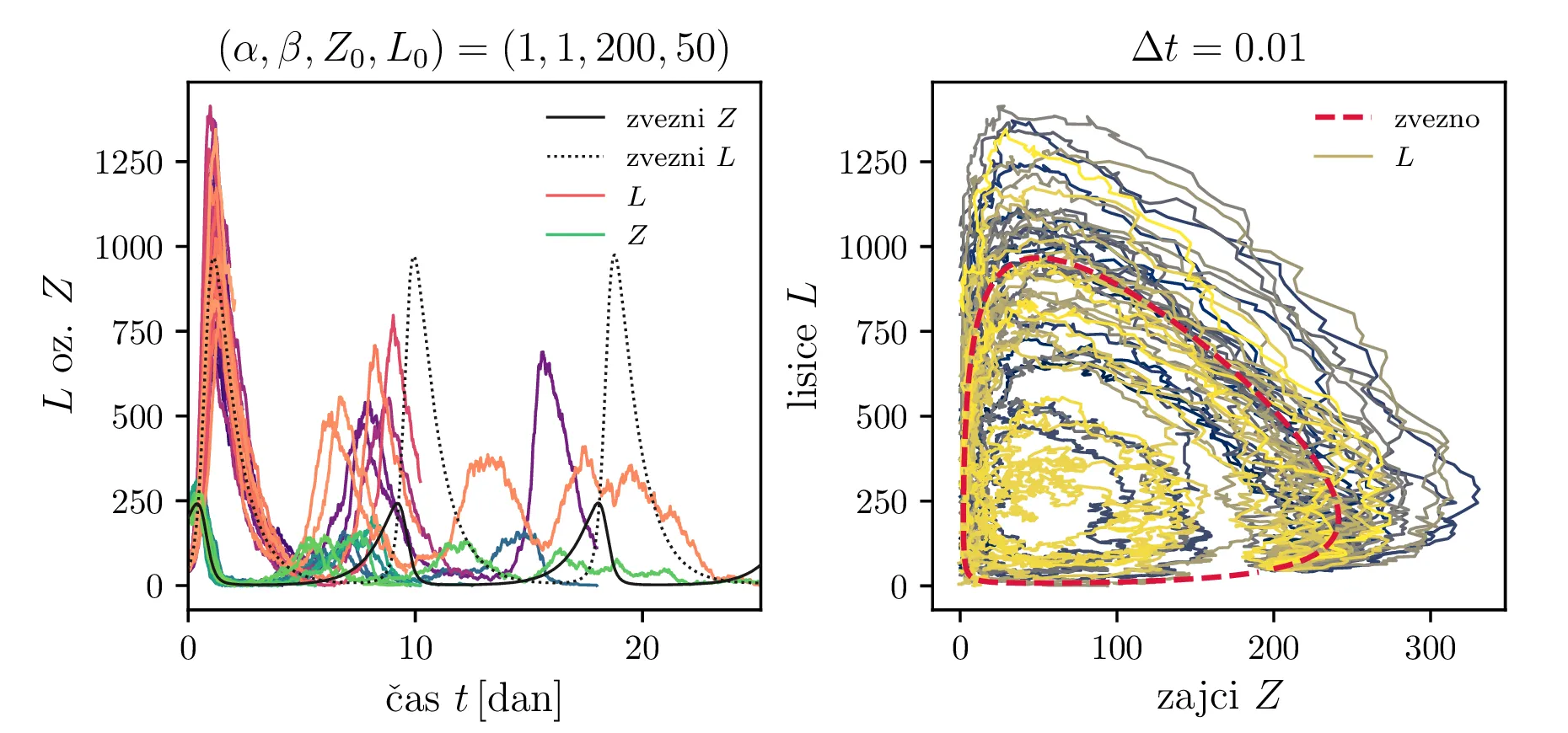
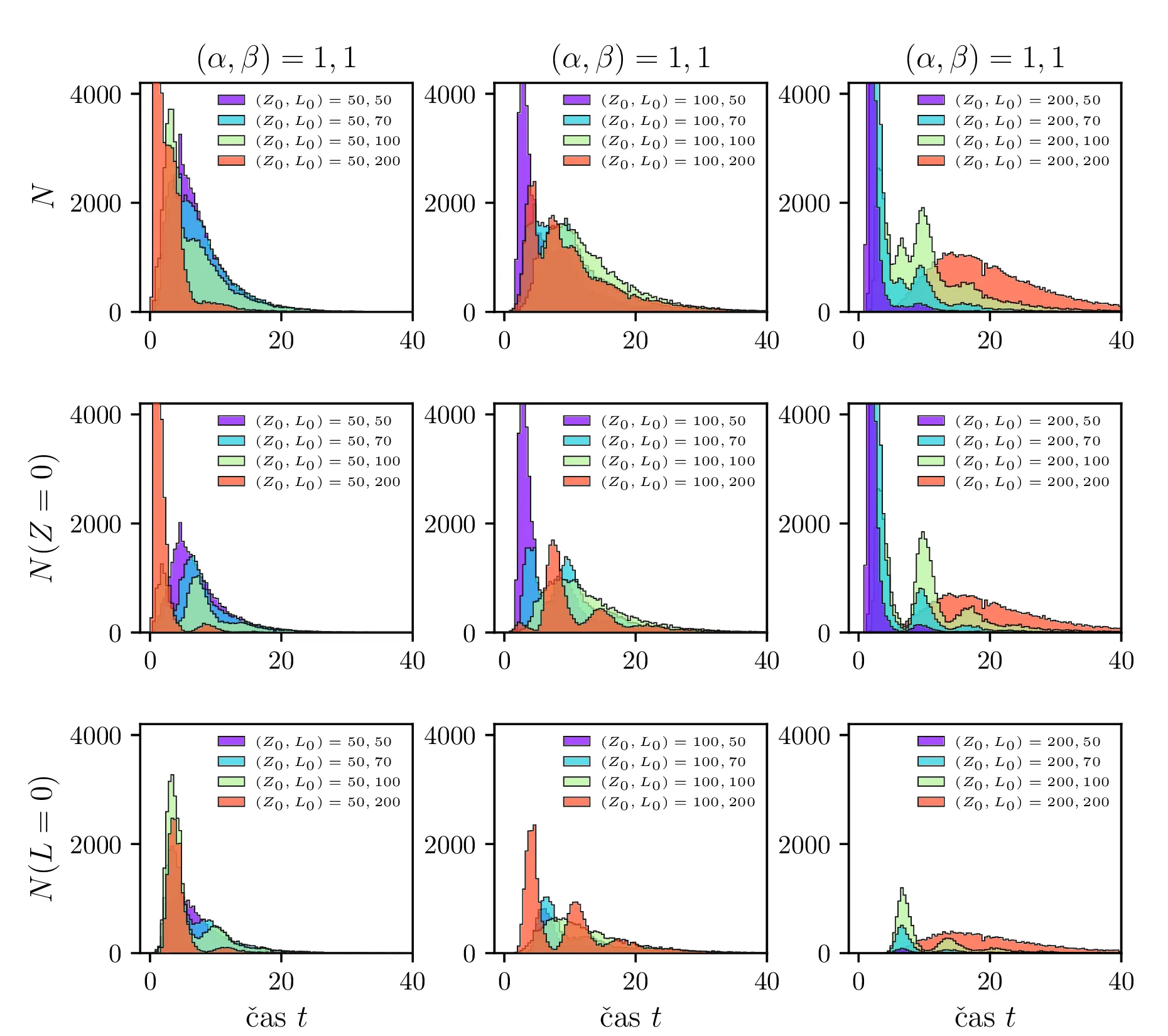
Stohastični Lotka-Volterra model opišemo z stohastično diferencialno enačbo, kjer rojstva in smrti opišemo z nasprotno predznačenimi Poissonovskimi \(\mathcal{P}\) členi, predacijo pa prav tako z Poissonovskimi členi \(\propto ZL\). Sistem stohastičnih enačb je torej \begin{equation}\begin{aligned} &Z(t + \Delta t) = Z(t) + \mathcal{P}(5\alpha Z \Delta t) - \mathcal{P}(4 \alpha Z \Delta t) - \left( \frac{\alpha ZL }{L_0} \right), \nonumber \\ &L(t + \Delta t) = L(t) + \mathcal{P}(4\beta L \Delta t) - \mathcal{P}(5 \beta L \Delta t) + \left( \frac{\beta ZL }{Z_0} \right), \label{eq:stohastic-lotka} \end{aligned}\end{equation} kar v zvezni ne-stohastični sliki ustreza sistemu navadnih diferencialnih enačb \[\begin{aligned} &\dot{Z} = \alpha Z - \alpha \frac{ZL}{L_0}, \nonumber \\ &\dot{L}= -\beta L + \beta \frac{ZL}{Z_0}. \end{aligned}\] Na sliki 11 vidimo primer 40 shohastičnih potekov \(Z, L\) populacij. V osnovi je obnašanje še vedno ciklično, le pri vsakem ciklu obstaja v minimumu populacije za vrsto možnost izumrtja le-te vrste. To se še lepše vidi na histogramih na sliki 15, kjer so v zgornji vrsti predstavljeni histogrami vseh izumrtij po času, v sredinski in spodnji vrsti pa vidimo histograme ločeno za izumrtja ene in druge vrste (zajcev in lisic). V teh ločenih histogramih vidimo jasne vrhove povečane verjetnosti za izumrtje vrste, ki ustrezajo periodičnih minimumom populacije za to vrsto.
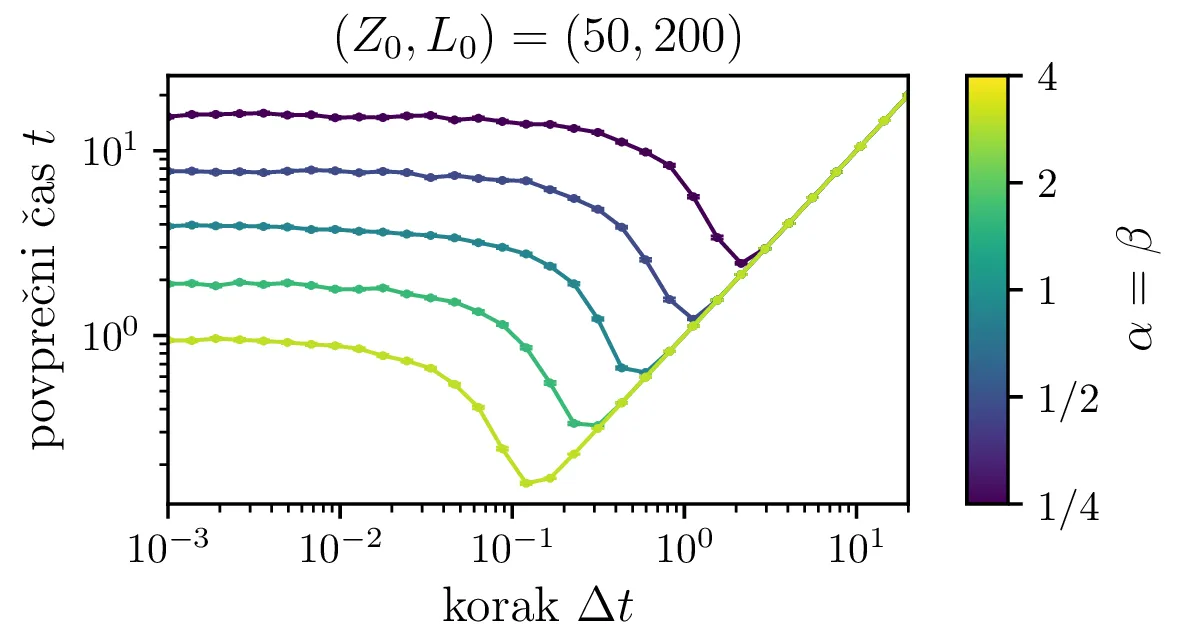
Na sliki 13 je narisana odvisnost povprečnih časov za neko izbiro \(\alpha = \beta\) od koraka stohastične integracije. Zgodba je povsem enaka kot s korakom integracije za proces izumiranja na sliki 7, potreben je dovolj majhen \(\Delta t\), za večje \(\alpha = \beta\) je potrebna izbira manjšega koraka.
Povprečni čas izumrtja
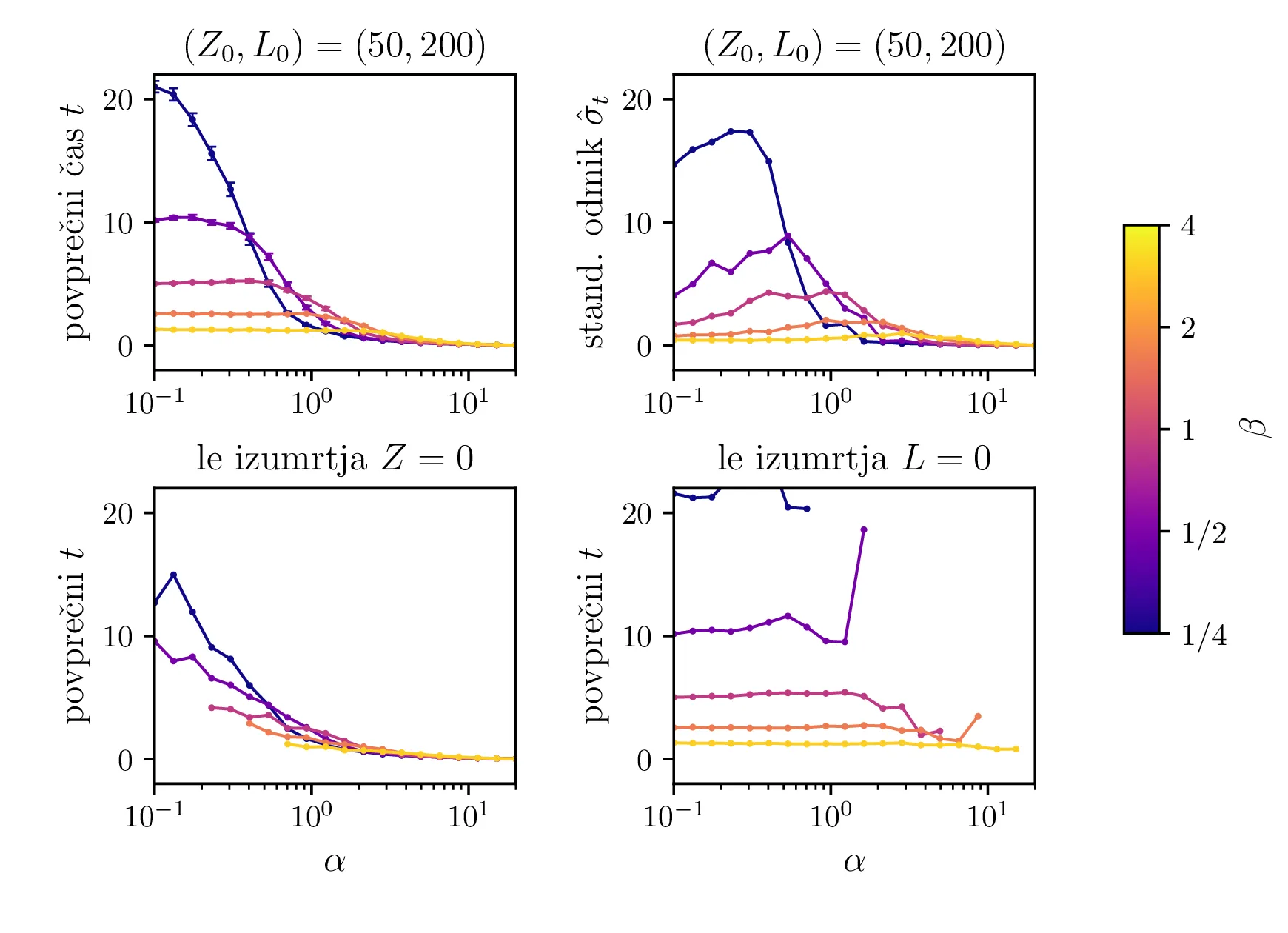
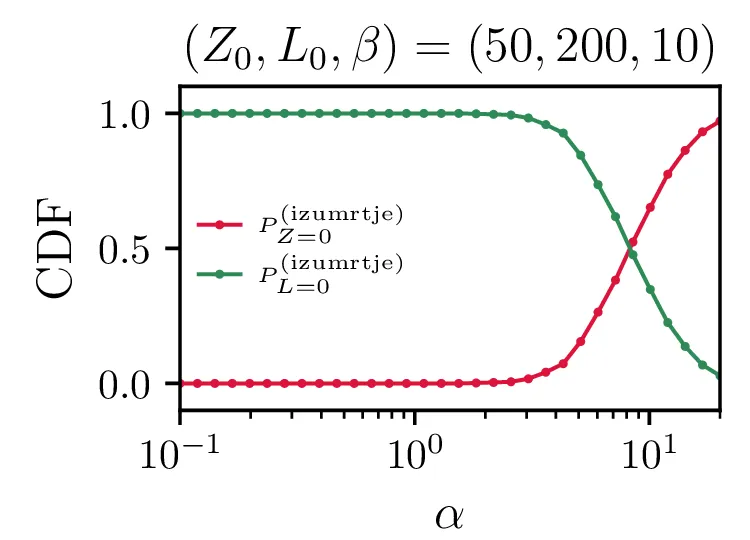
Na sliki 12 so predstavljeni povprečni časi izumrtja za različne hitrosti \(\alpha\) in \(\beta\). Spet ločimo dogodke izumrtja na izumrtja zajcev \(Z = 0\) in izumrtja lisic \(L = 0\). Na sliki 12 spodaj se ločeno vidita povprečna časa za izumrtja zajcev in izumrtja lisic. Za \(\alpha \ll \beta\) na grafu izumrtij \(Z = 0\) ni več točk, saj so dogodki tako redki, da jih sploh ne zajamemo (ali pa jih zajamemo res majhno število in je dobljeno povprečje povsem nezanesljivo). Obratno je za režim \(\alpha \gg \beta\) očiten manjko točk na grafu izumrtij \(L = 0\). V tem režimu so vice-versa izjemno redka izumrtja lisic.
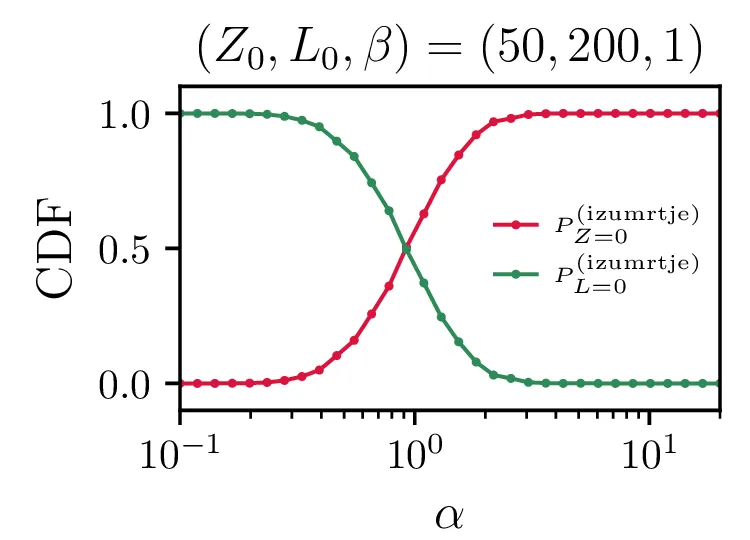
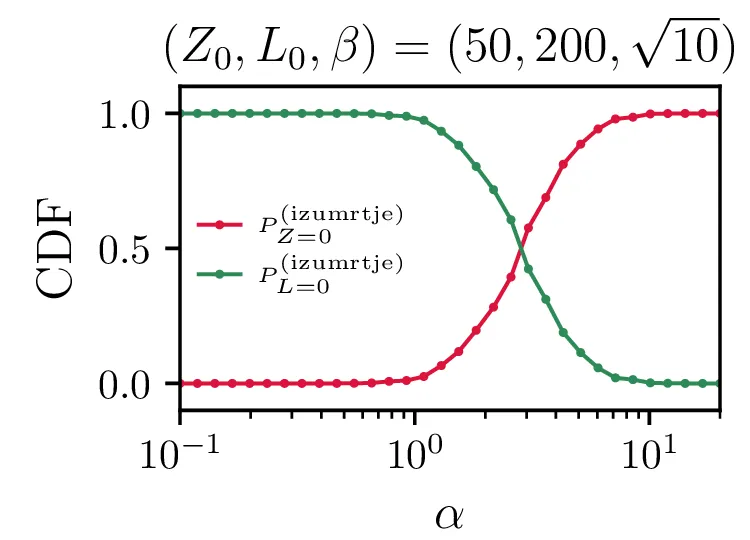
Še bolj eksplicitno je prehod med tema dvema režimoma izumiranj prikazan na sliki 14, kjer je očiten prehod iz izumiranja lisic za \(\alpha \ll \beta\) v izumiranje zajcev za \(\alpha \gg \beta\).
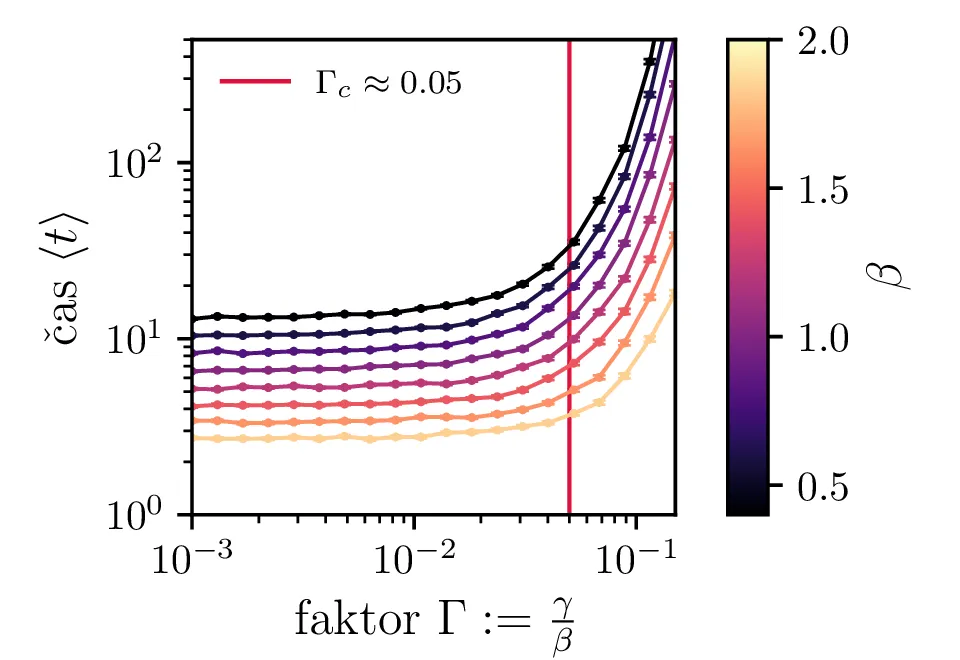
Shohastični model epidemije
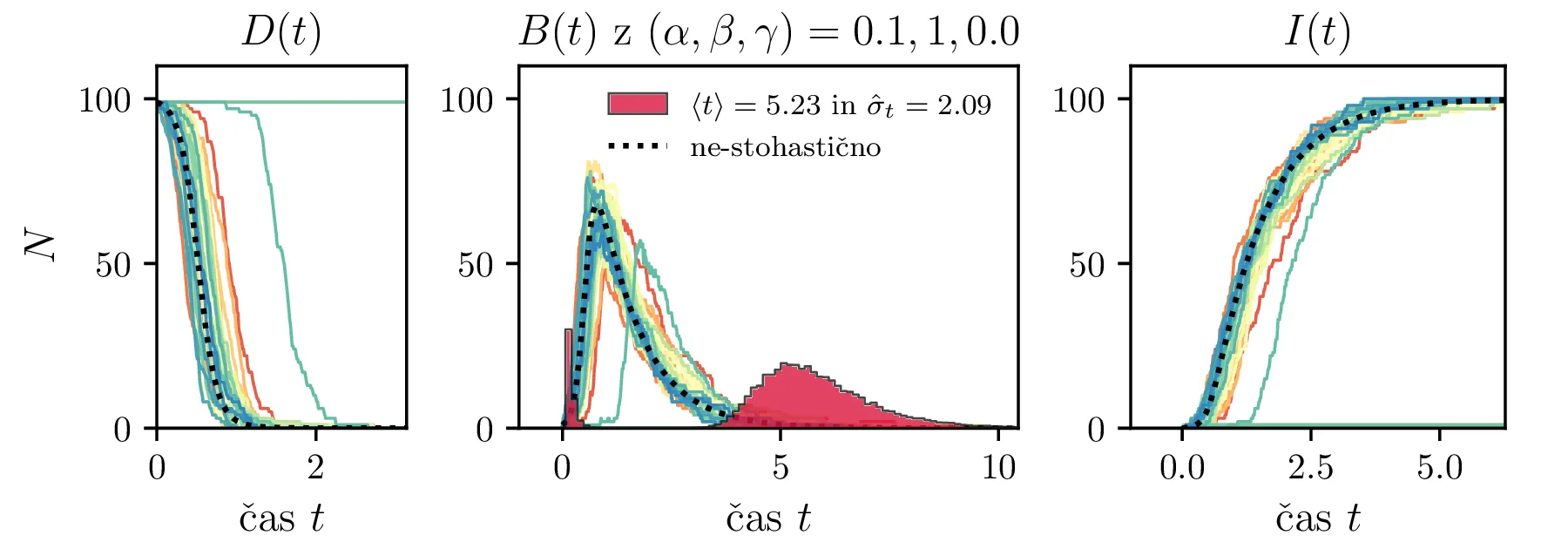
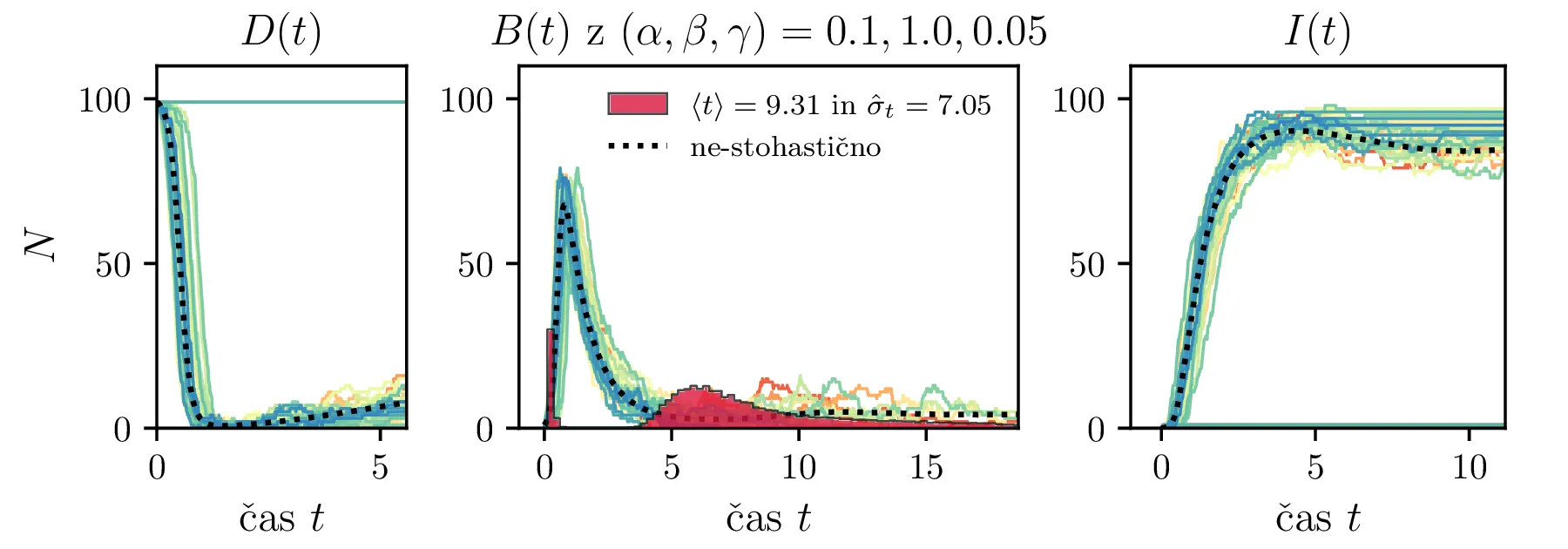
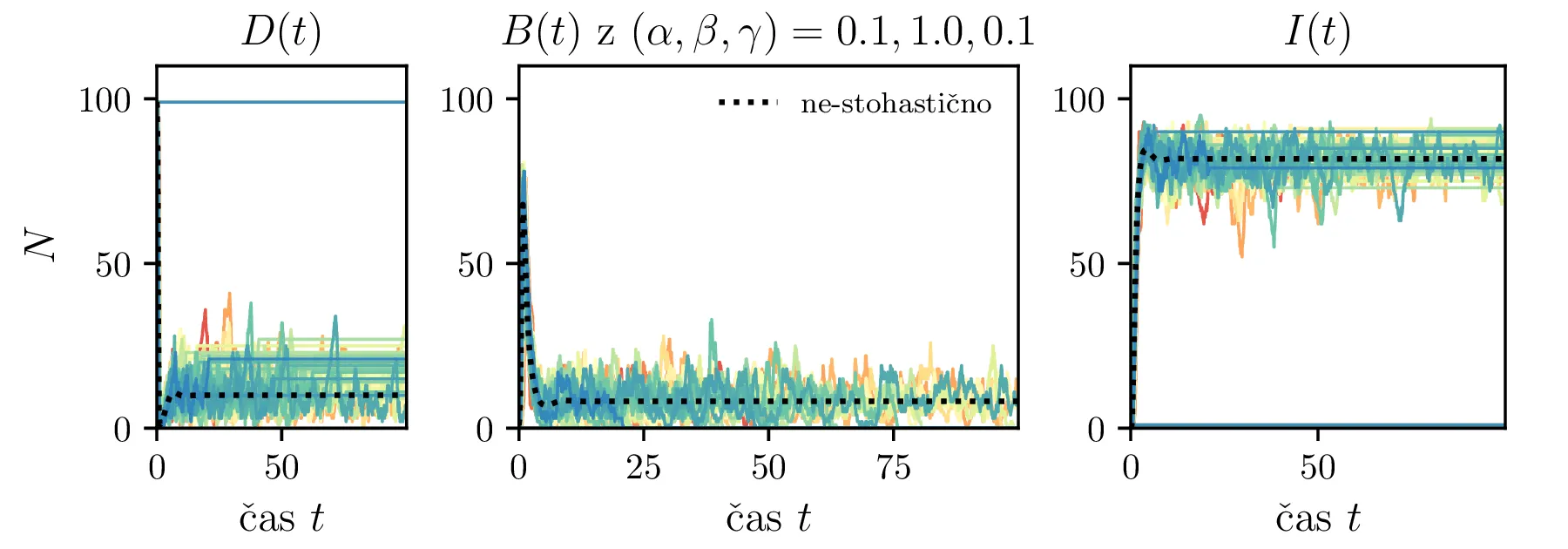
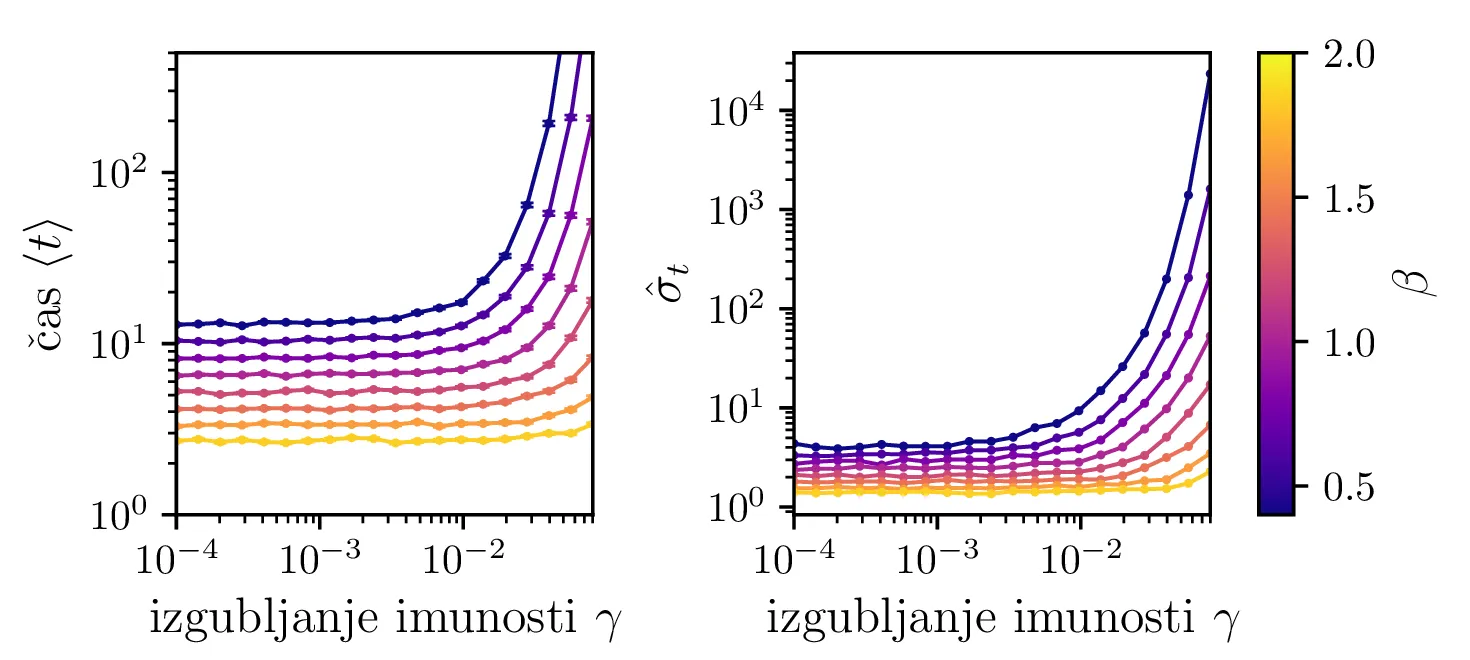
Podobno kot v 4. nalogi bomo časovni razvoj epidemije opisovali z sistemom diferencialnih enačb za tri razrede dovzetnih \(D\), bolnih \(B\) in imunih \(I\). Dodali bomo tudi člen \(-\gamma I\), ki bo opisoval popuščanje imunosti v nekem času \(\tau_\mathrm{pop. imunosti} = \frac{1}{\gamma}\). Sistem ne-stohastičnih enačb tedaj zapišemo kot \[\begin{aligned} \dot{D} &= -\alpha DB + \gamma I, \nonumber \\ \dot{B} &= \alpha DB - \beta B, \\ \dot{I} &= \beta B - \gamma I \nonumber. \end{aligned}\] Preprosto je videti, kako tak zvezni model preslikamo v sistem stohastičnih diferencialnih enačb. Kar brez dolgovezenja zapišemo \begin{equation}\begin{aligned} &D(t + \Delta t) = D(t) -\mathcal{P}(\alpha DB \Delta t) + \mathcal{P}(\gamma I \Delta t), \nonumber \\ &B(t + \Delta t) = B(t) + \mathcal{P}(\alpha DB \Delta t) - \mathcal{P}(\beta B \Delta t), \label{eq:stohastic-DBI} \\ &I(t + \Delta t) = I(t) + \mathcal{P}(\beta B \Delta t) - \mathcal{P}(\gamma I \Delta t) \nonumber. \end{aligned}\end{equation} Na sliki 16 vidimo primerjavo med procesom za model pri \(\gamma = 0\), t. j. ko pridobljena imunost pacienta ne popusti in modelom z neko hitrostjo popuščanja \(\gamma = 0.05\). Tako popuščanje znatno podaljša epidemijo, kar se pozna na veliko daljšem desnemu repu histograma po časih konca epidemije. Poveča se tako povprečni čas kot tudi njegova varianca, eksplicitno to narišemo na sliki 18, kjer je vidno, da za dovolj majhne \(\beta = 1\), t. j. za dolgožive bolezni, trajanje epidemije zelo občutljivo na popuščanje imunosti. Da je to res pogojeno s kombinacijo dolgožive bolezni in z popuščanjem imunosti, lahko vidimo z uvedbo parametra \(\Gamma \vcentcolon=\frac{\gamma}{\beta}\), kjer je odvisnost lepša in kriterij za izjemno dolgo trajajočo epidemijo je približno \[\Gamma > \Gamma_c, \quad \Gamma_c \approx 0.05,\] kot to vidimo na sliki 18 spodaj, kjer vsi časi hkrati poskočijo nekje približno pri \(\Gamma_c \approx 0.05\). Za večje \(\Gamma \gg \Gamma_c\) so epidemije pričakovano lahko izjemno dolge, kot to vidimo vsaj ilustrirano na primeru 17.