Modelska analiza I
8. naloga: Metropolis-Hastings algoritem

Navodila

1. Molekularna verižnica. 17 členkov dolga nitkasta molekula je obešena za oba konca. Vsak členek se lahko povesi od ničelne lege na poljubnega od 19 nivojev in si s tem zmanjša potencialno energijo za eno enoto na nivo. Če pa s tem prenategne vezi do sosedov, plača s prožnostno energijo, ki je za vsakega soseda enaka kvadratu razlike v nivojskem številu. Določi ravnovesno energijo v odvisnosti od temperature. Za poteze lahko uporabiš spremembo za en nivo na izbranem slučajnem mestu.

2. Isingov model. Feromagnetne in antiferomagnetne snovi v dveh dimenzijah v približku dveh stanj opišemo s Hamiltonovim operatorjem \begin{equation}\mathcal{H} = −J \sum_{\langle ij \rangle} s_i s_s − H \sum_{i} s_i, \quad J = \pm 1 \label{eq:hamiltonian}\end{equation} kjer je \(s_i = \pm 1\) in vsota teče le po vezeh \(\langle ij \rangle\) med najbližjimi sosedi. Če ni zunanjega polja (\(H = 0\)), temperatura \(T_c\) faznega prehoda pri feromagnetu zadošča enačbi \[\sinh \left( \frac{2J}{k T_c} \right) = 1,\] kar je približno enako \[T_c \approx 2.269185 \frac{J}k.\] Določi povprečno energijo \(\langle E \rangle\) in lastno magnetizacijo \(\langle S \rangle\) v odvisnosti od temperature. \(S = \sum_{i=1}^N s_i\) je celotna magnetizacija sistema. Oglej si tudi spinsko susceptibilnost in specifično toploto pri različnih jakostih magnetnega polja. \begin{equation}\chi = \frac{\langle S ^2 \rangle - \langle S \rangle^2}{N kT}, \quad c = \frac{\langle E^2 \rangle - \langle E \rangle^2}{N kT^2}. \label{eq:susept}\end{equation}

Molekularna verižica

Molekularna verižica je sestavljena iz molekul \(i = 1, 2, \dots 17\), ki jih opisujejo položaji \(h_1, h_2, \dots, h_{17}\). Njena energija je enaka \begin{equation}\mathcal{E} = \alpha \sum_{i = 1}^{17} h_i + \frac{1}{2} \sum_{i = 2}^{17} (h_{i-1} - h_i)^2. \label{eq:energy}\end{equation} Stanja verižice so omejena v nekem intervalu \(h_i \in [h_\mathrm{min} 0]\), pri čemer je \(h_\mathrm{min} < 0\) neko število ali pa \(-\infty\). Za obnašanje sistema je pomemben faktor \(\alpha\), ki določa pomen potencialne energije, večji \(\alpha\) opisuje sistem, kjer prevladuje potencialna energija. Sistem bomo simulirali z Monte-Carlo simulacijo. Poglavitna ideja za Monte-Carlo simulacijo takega sistema je to, da žrebamo vzorce mikrostanj \(\Omega\) iz Boltzmannove porazdelitve \[\mathrm{PDF}[\Omega] = e^{-\mathcal{E}(\Omega) / kT}.\] Žrebanje mikrostanj za Monte-Carlo simulacijo bomo izvajali z Metropolisovim algoritmom

1. Začnemo z neko naključno porazdelitvijo \(h_i \sim U(0, \mathop{\mathrm{max}}(-20, h_\mathrm{min}))\), le za \(h_1 = h_{17} = 0\).

2. Na posameznem koraku predlagamo potezo \(h_{i} \mapsto h_i + \delta_i\) za naključna \(i = 2, 3, \dots, 16\) in \(\delta_i = \pm 1\).

3. Predlagano potezo sprejmemo, če je \(\Delta\mathcal{E} < 0\), pri čemer je \(\Delta \mathcal{E} = \delta_i^2 - \delta_i (h_{i+1} - 2h_i + h_{i-1} - \alpha)\).

4. Predlagano potezo sprejmemo tudi v primeru, da je \(\Delta\mathcal{E} > 0\), a le z verjetnostjo \(P_\mathrm{sprejetja} = e^{-\Delta \mathcal{E} / T}\) (tu uporabljamo brezdimenzijsko temperaturo, glej 2.1).

5. Naslednji korak. Ponovimo korak 2.

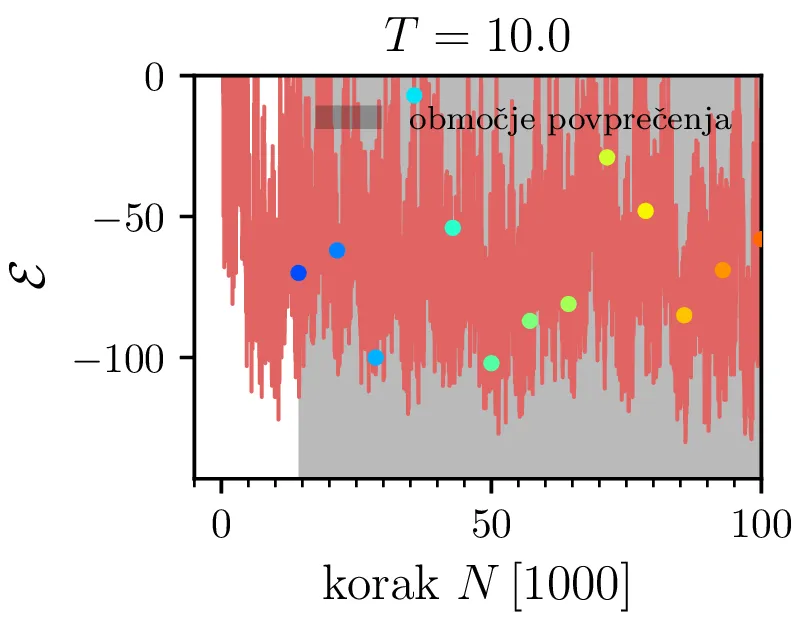
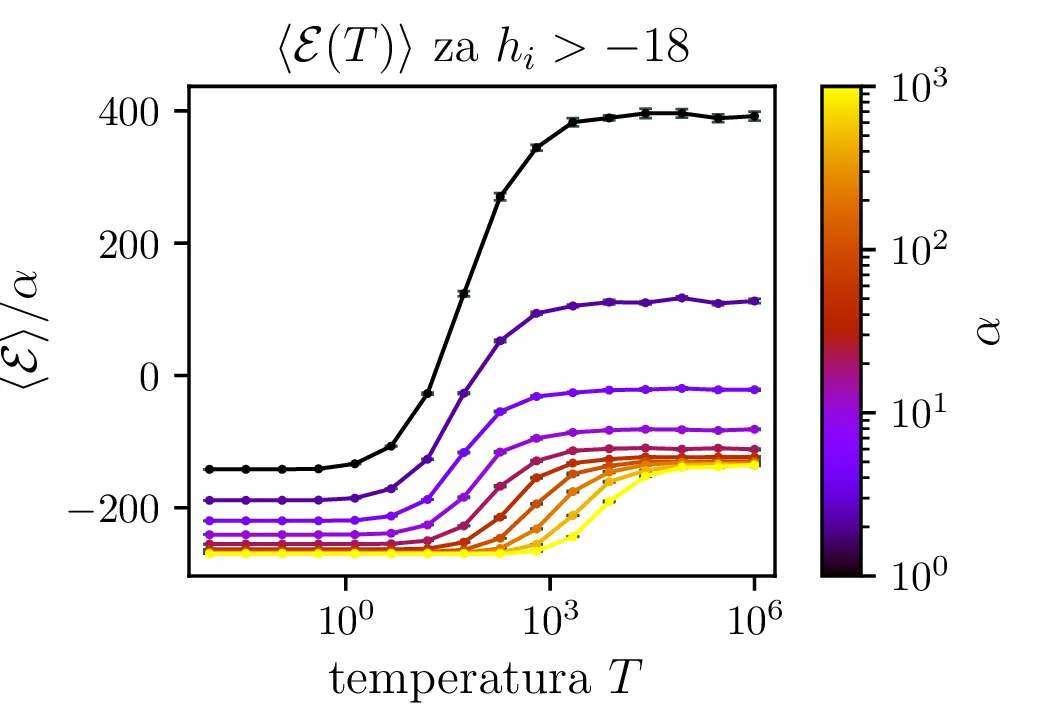
Primere mikrostanj žrebanih z Metropolisovim algoritmom vidimo na sliki 3 za omejeno verižico \(h_i > -18\) in na sliki [fig:ensabmle-nolim] za neomejeno verižico. Tako kot to velja za energije v poteku integracije 1, je tudi za konfiguracije očiten vpliv temperature, ki povzroči večje fluktuacije. Ko vzorčimo za namen dejanske integracije, npr. za izračun \(\langle \mathcal{E} \rangle\), si izberemo tudi nek t. i. burn-in periodo, v kateri vzorčenje po Metropolisovem algoritmu še ni prešlo v stacionarno porazdelitev (Markova veriga še ni stacionarna). Tako območje, npr. prvih \(20\%\) na sliki 1 izločimo iz naših vzorcev, s katerimi bomo v nadaljevanju računali.

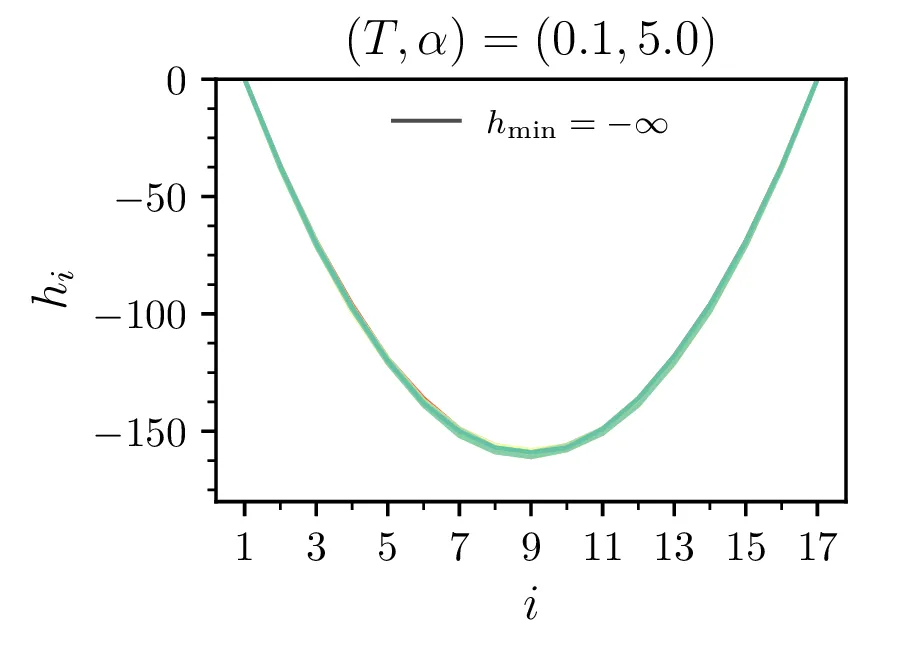
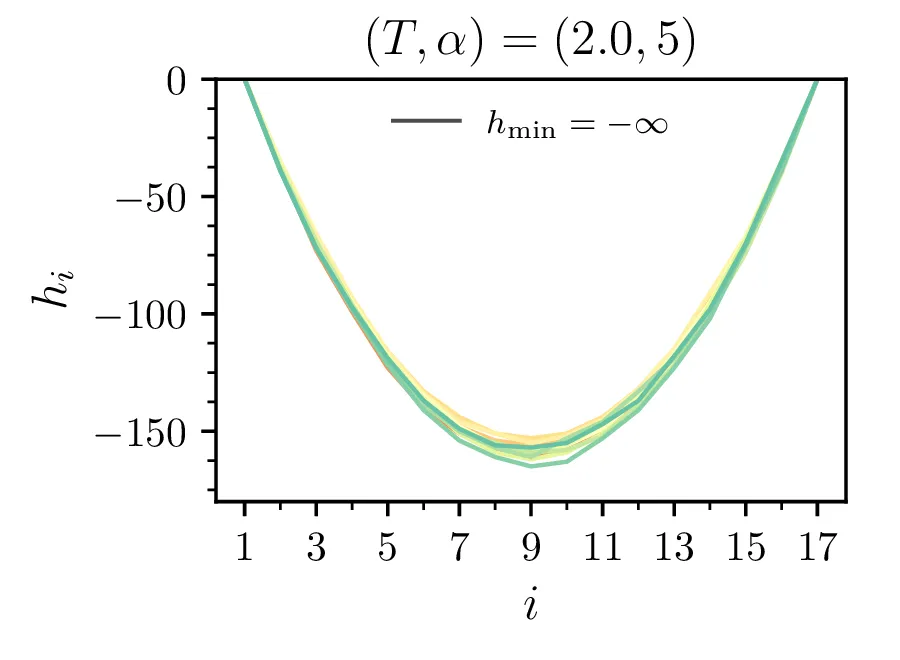
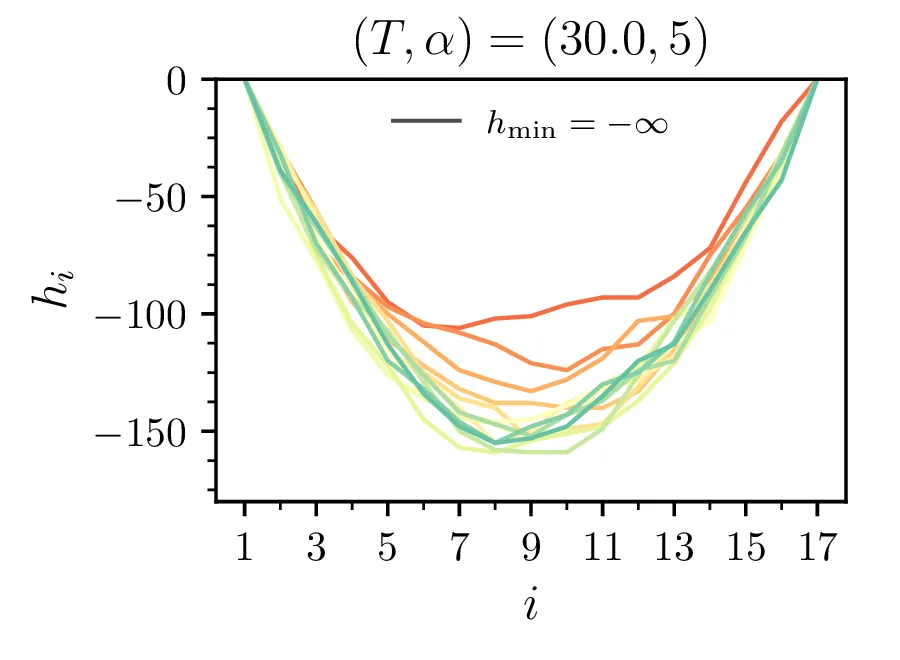
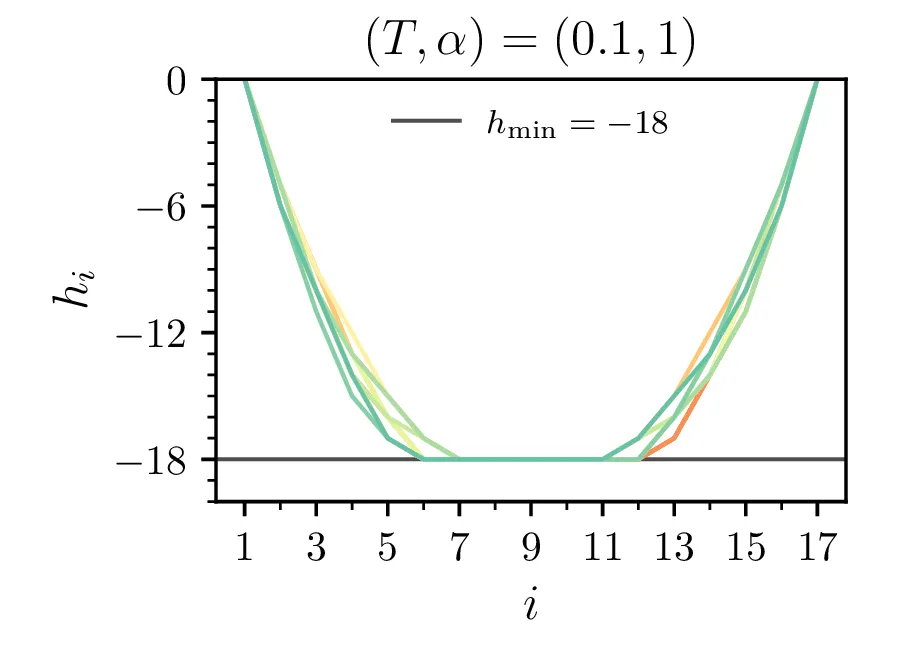
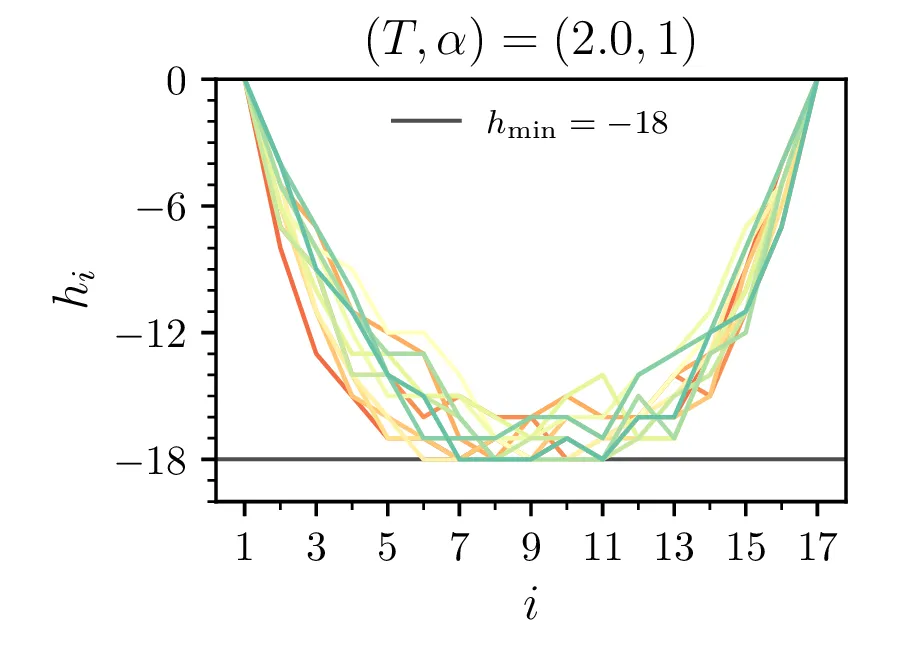
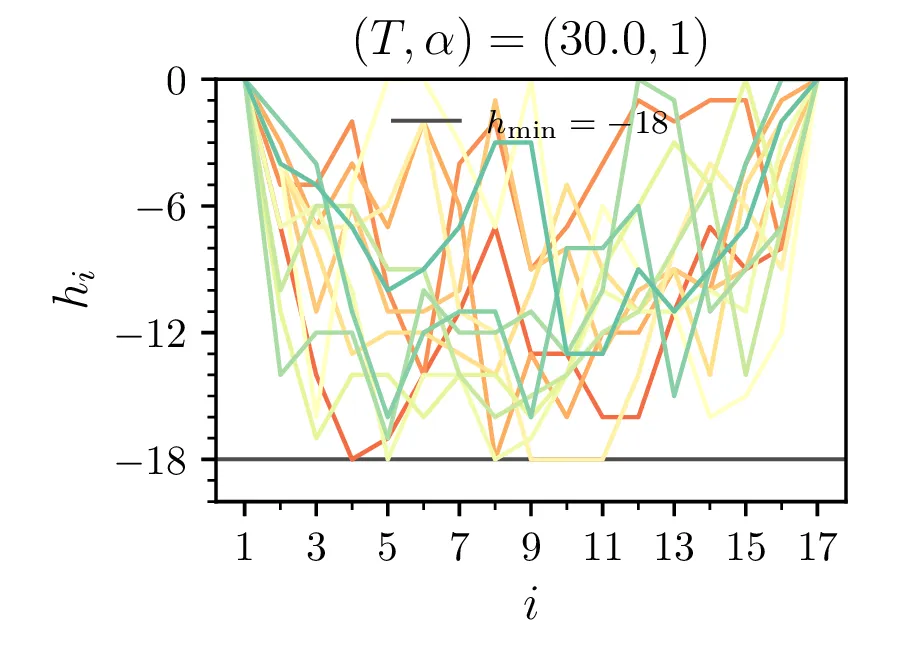
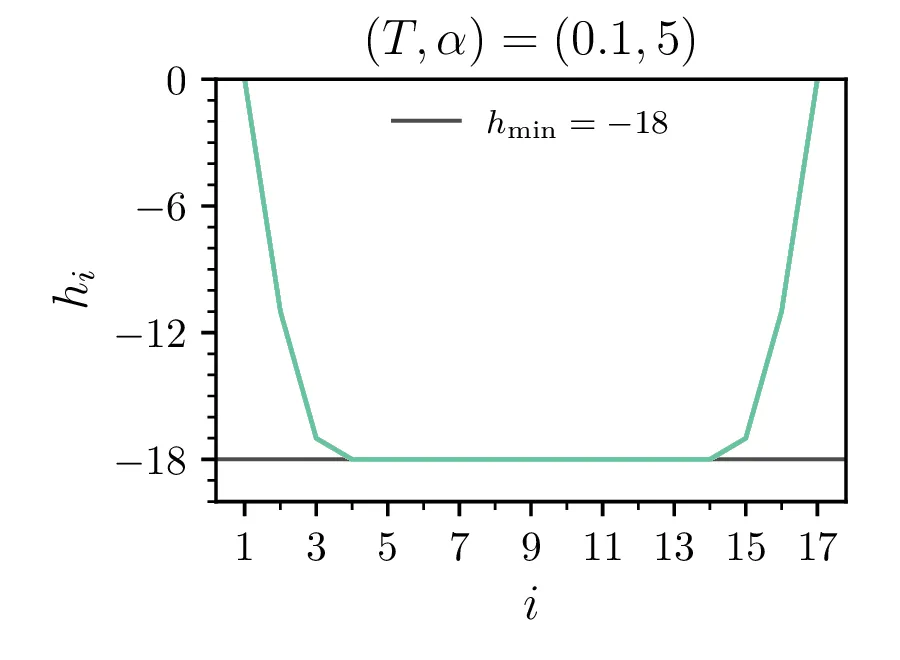
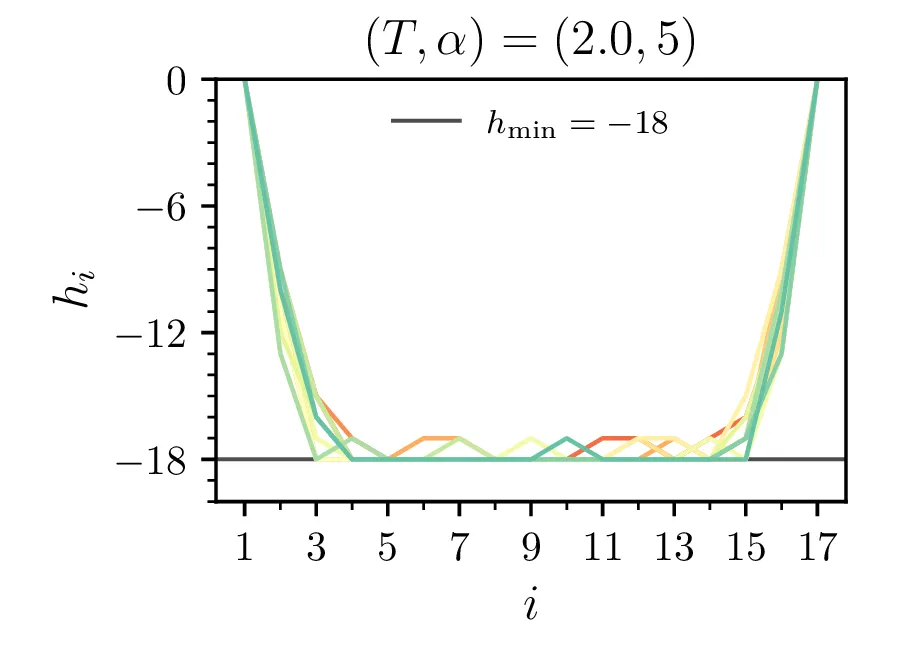
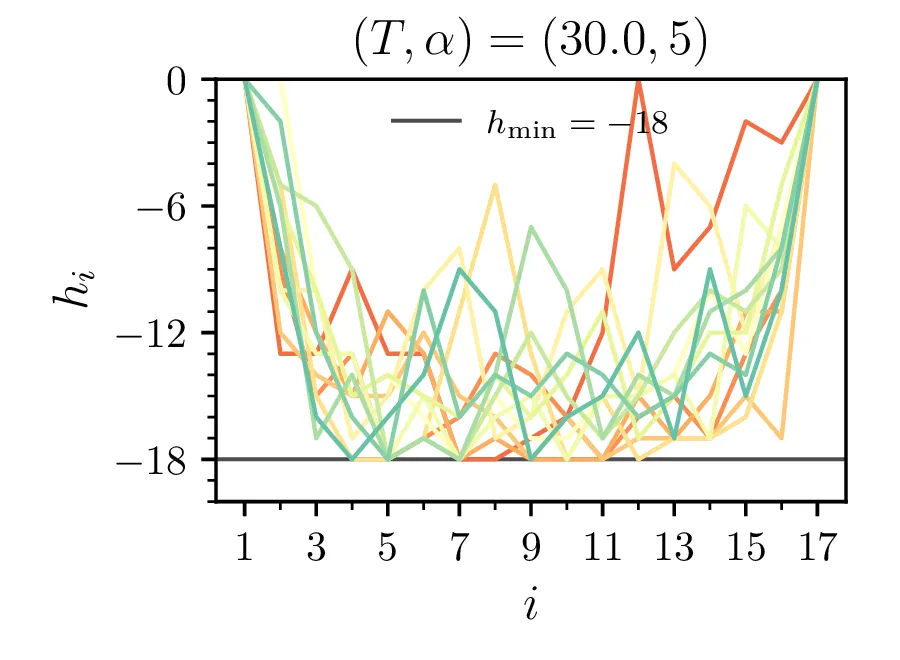
Brezdimenzijska temperatura

Ker je energija 3 brezdimenzijska, je nekako nesmiselno, da ima naš \(kT\) dejanske enote. Zato bomo za brezdimenzijsko vzeli tudi našo temperaturo \(T\), glede enot pa bomo postopali sledeče. Če energiji \(\mathcal{E}\) pripišemo neko enoto \(E_\mathrm{enota}\), lahko določimo tudi enotsko temperaturo po zvezi \[E_\mathrm{enota} = k T_\mathrm{enota}.\] Boltzmannovi faktorji \(e^{-E / kT_\mathrm{Kelvin}}\) so tedaj v naših brezdimenzijskih oblikah kar enaki \(e^{-\mathcal{E} / T}\), pri čemer je enota za temperaturo enaka \(T_\mathrm{enota} = E_\mathrm{enota} / k\).

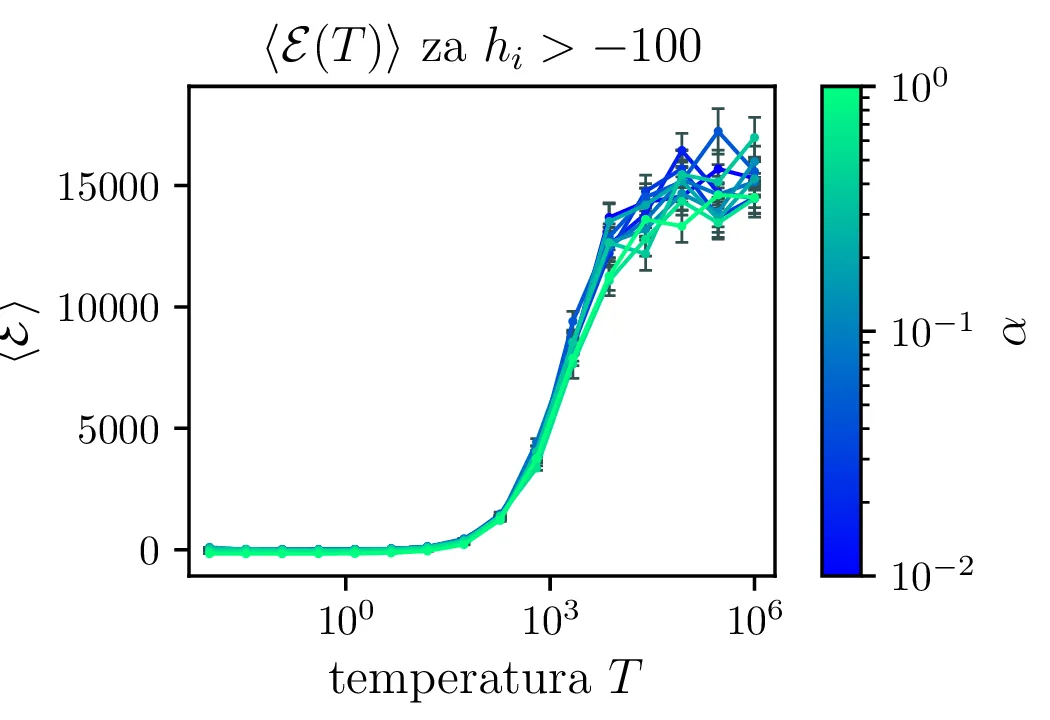
Temperaturna odvisnost energije

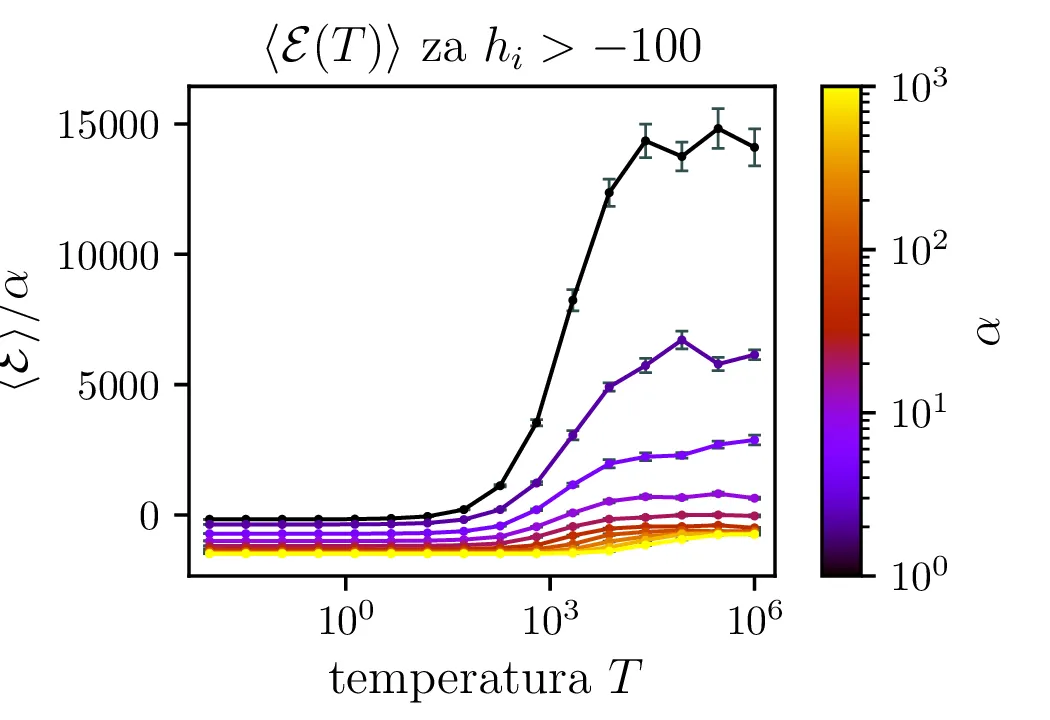
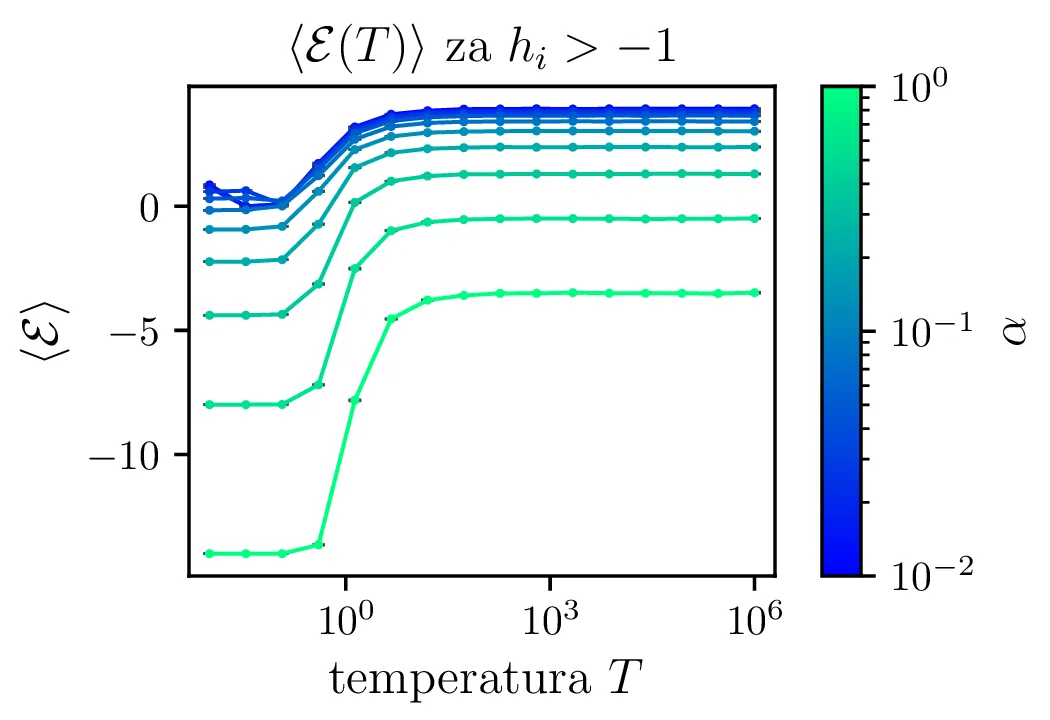
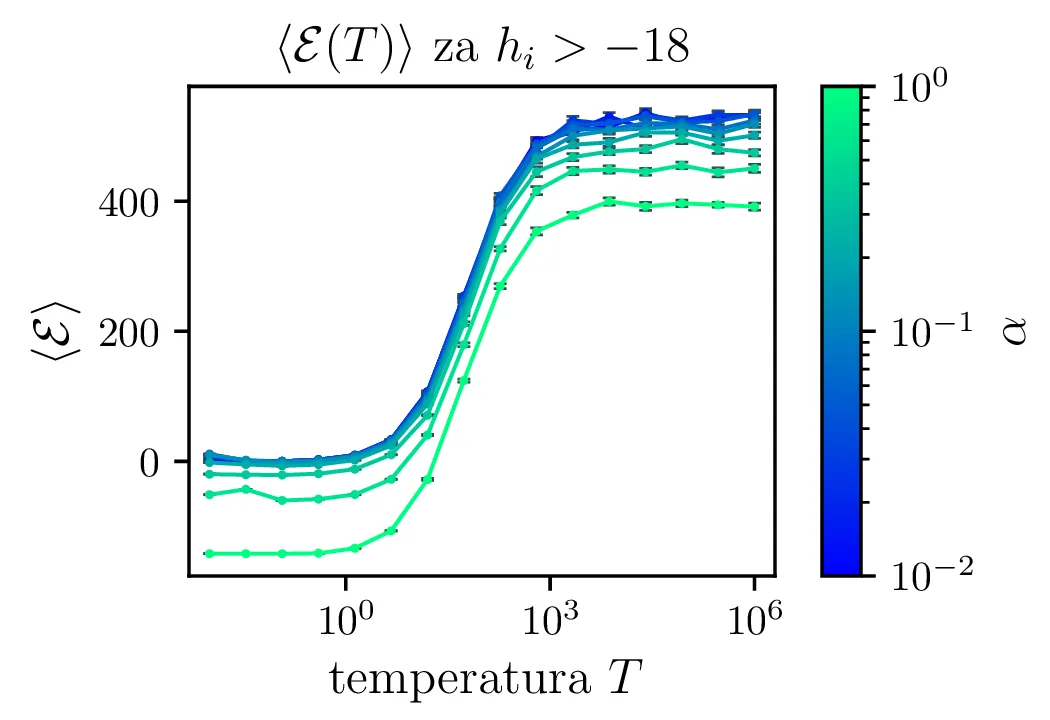
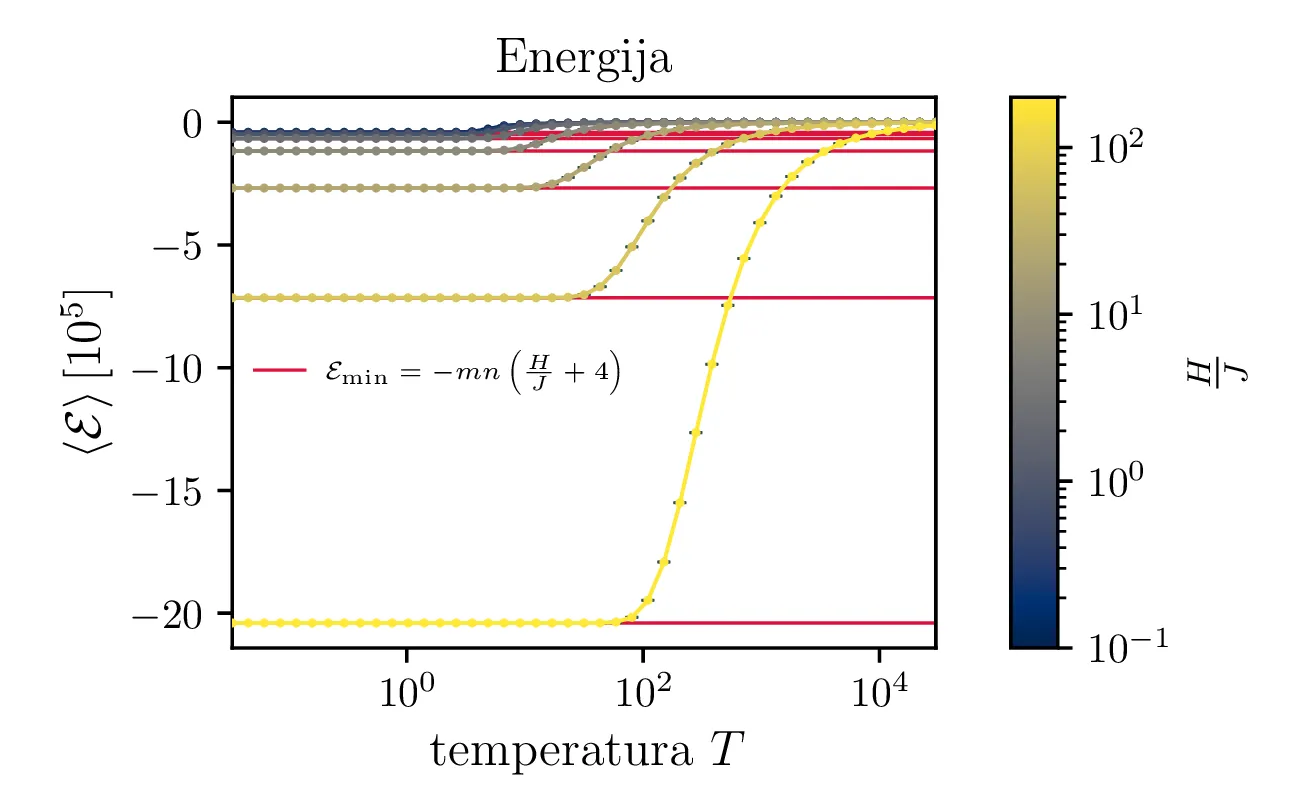
Na sliki 5 vidimo temperaturno odvisnost pričakovane energije. Iz odvisnosti \(\langle \mathcal{E} \rangle(T)\) lahko za lepšo preglednost faktoriziramo odvisnost \(\langle \mathcal{E} \rangle(T) \propto \alpha\), ki jo v nizkotemperaturni "limiti" jasno vidimo na sliki 4.

Ocena variance

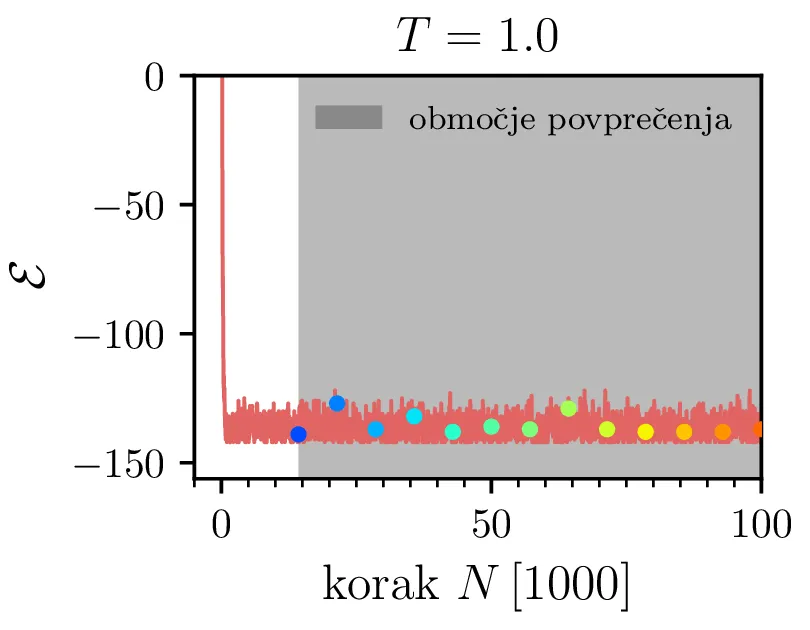
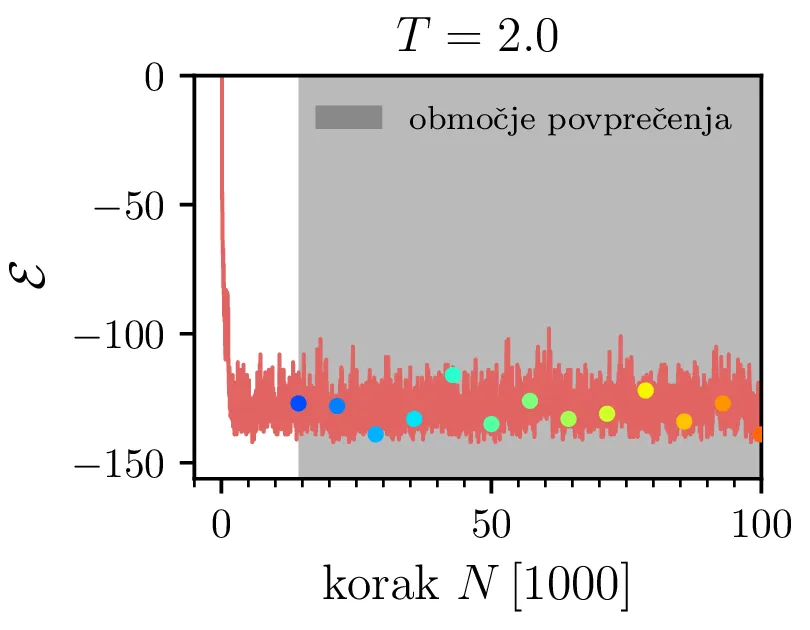
Varianco integracije bomo ocenili z povprečji neprekrivajočih batch-ov [1, Pogl. 1.10.1]. Prvo izberemo neko burn-in periodo izločenih vzorcev, npr. prvih \(20\%\) vzorcev kot prikazano na sliki 1. Nato območje po burn-in periodi razdelimo na 20 razdelkov \(k = 1, 2, \dots, 20\) in za vsakega izmed njih izračunamo povprečje. Standardno napako naše integracije tedaj ocenimo kot varianco teh 20 agregatov \[\mathrm{SE} \approx \sqrt{ \frac{\mathop{\mathrm{Var}} {[\langle S \rangle_k]_{k=1}^{20}}}{20}}.\]

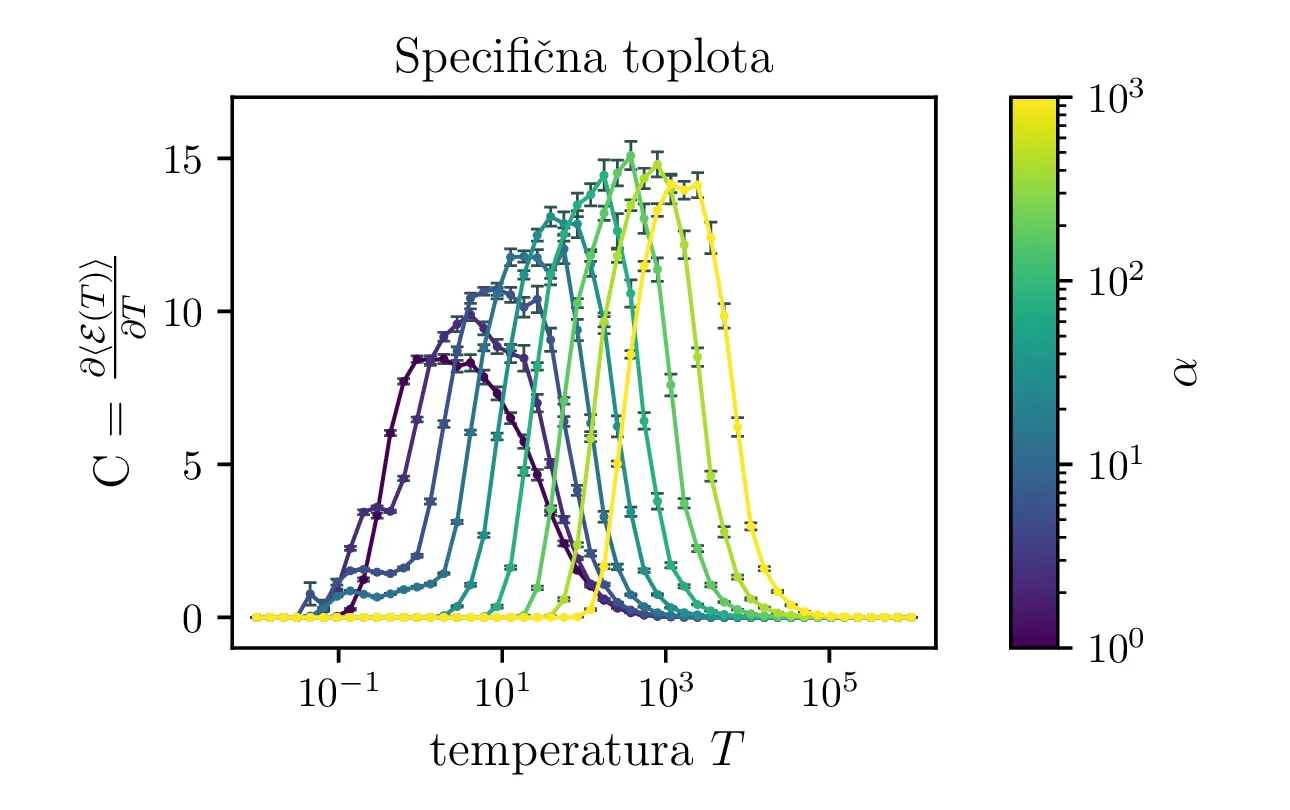
Specifična toplota

Za molekularno verižico nas zanima tudi specifična toplota. To bomo ocenili po t. i. Fluctuation-dissipation izreku [2], po katerem je specifična toplota kar sorazmerna z varianco energije našega sistema. To lahko preprosto pokažemo preko statistične fizike. Če je particijska funkcija sistema enaka \[Z = \int e^{-\beta \mathcal{E}} \,\mathrm{d}\Omega,\] lahko pričakovano vrednost energije izračunamo preko odvoda \(\ln Z\), specifična toplota pa je v nadaljevanju kar odvod \(\langle \mathcal{E} \rangle\) po temperaturi \[\langle \mathcal{E} \rangle = -\frac{\partial \ln Z}{\partial \beta} = \frac{\int \mathcal{E} e^{-\beta \mathcal{E}} \,\mathrm{d}\Omega}{\int e^{-\beta \mathcal{E}} \,\mathrm{d}\Omega},\] \[C \vcentcolon=\frac{\partial \langle \mathcal{E} \rangle}{\partial \beta} \frac{\mathrm{d}\beta}{\mathrm{d}T} = \frac{\partial}{\partial \beta} \left( \frac{-1}{Z} \frac{\partial Z}{\partial \beta} \right) \left( \frac{-1}{kT^2} \right) = \frac{1}{kT^2} \left( \frac{1}{Z} \frac{\partial^2 Z}{\partial \beta^2} - \frac{1}{Z^2} \left( \frac{\partial Z}{\partial \beta} \right)^2 \right).\] Ker je \(\frac{\partial^2 Z}{\partial \beta^2} / Z\) kar pričakovana vrednost \(\langle \mathcal{E} \rangle\), lahko zaključimo, da je specifična toplota enaka kar varianci energije za porazdelitev podano z particijsko funkcijo \begin{equation}C = \frac{\langle \mathcal{E}^2 \rangle - \langle \mathcal{E} \rangle^2}{kT^2} = \frac{\mathop{\mathrm{Var}} [\mathcal{E}]}{kT^2} \label{eq:specific-heat}\end{equation} To je zelo prikladno za izračun z MC metodo, saj je varianco \(\mathop{\mathrm{Var}} [\mathcal{E}]\) preprosto izračunamo na območju, na katerem smo računali npr. energijo (sivo območje na 1). Tako izračunana specifična toplota za \(h_i > -18\) je prikazana na sliki 6.

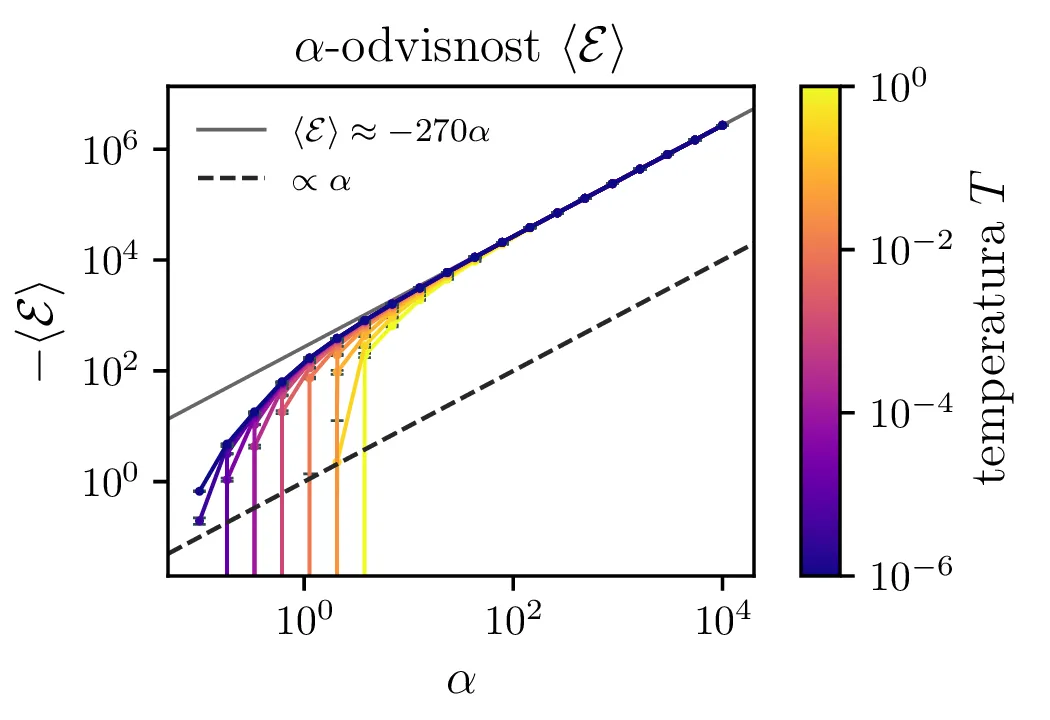
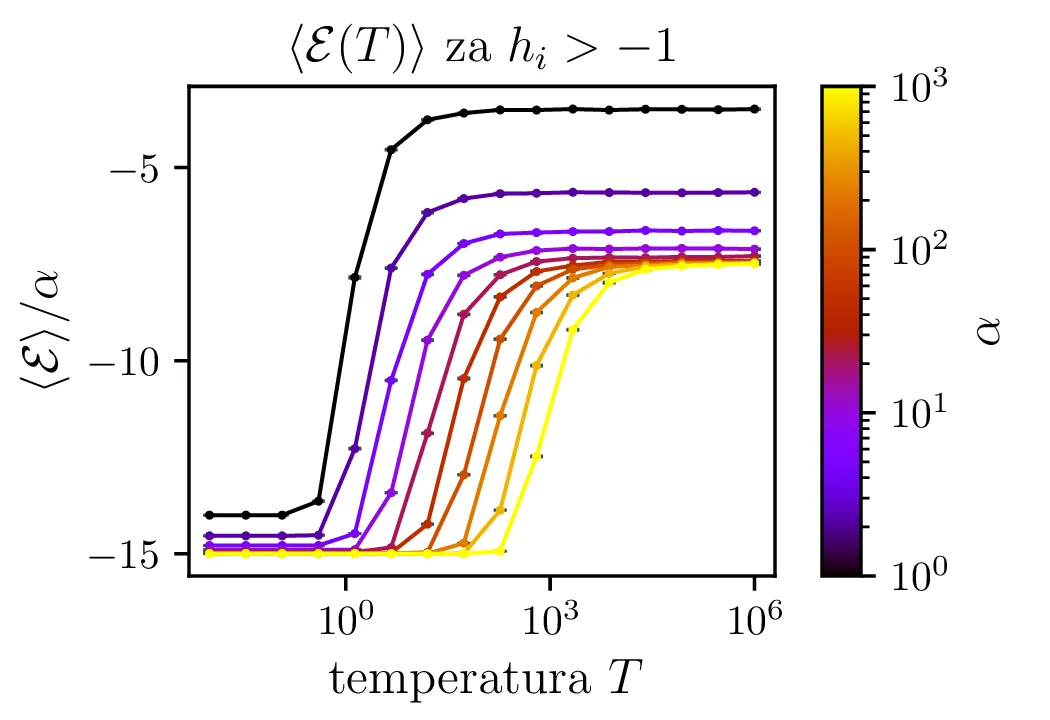
Isingov model

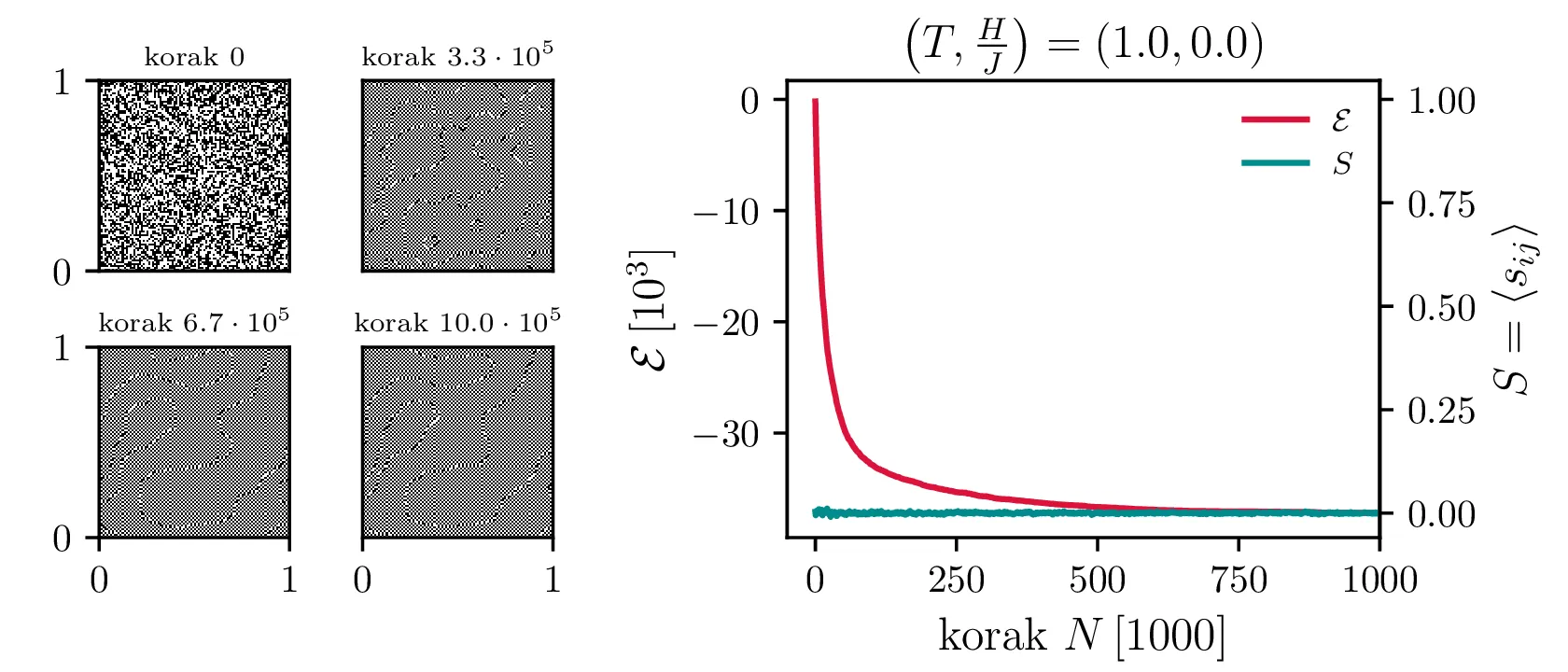
Isingov model je opisan z Hamiltonianom 1. Prvo se bomo znebili enega parametra tako, da bomo zapisali \(\mathcal{E} = \mathcal{H} / J\) \[\mathcal{E} = −\sum_{\langle ij \rangle} s_i s_j − \left(\frac{H}{J}\right) \sum_{i} s_i, \quad J = \pm 1.\] Tedaj obnašanje sistema določa Boltzmannov faktor \(e^{-\mathcal{E} / T}\), pri čemer je \(T\) brezdimenzijska temperatura v enotah \[T_\mathrm{enota} = \frac{J}{k}.\] Obnašanje sistema je povsem določeno z dvema spremenljivkama \((T, H/J)\)¹. Simulirali ga bomo z Metropolisovim algoritmom, ki se od tistega za molekularno verižico razlikuje le po tem, kako izbiramo naše naključne poteze, to je t. i. proposal distribution in po tem, kakšna je sprememba energije za take možne poteze. Če še enkrat zapišemo algoritem v celoti

1. Začnemo z neko \(m\times n\) naključno porazdelitvijo dimenzije \(S_{ij} \in \{ -1, 1 \}\).

2. Na posameznem koraku predlagamo potezo \(S_{ij} \mapsto -S_{ij}\) za naključno mesto \((i,j)\).

3. Predlagano potezo sprejmemo, če je \(\Delta \mathcal{E} < 0\), pri čemer je \[\Delta \mathcal{E} = 2S_{ij} \left( S_{i-1,j} + S_{i+1,j} + S_{i,j-1} + S_{i,j+1} \right) + 2\left(\frac{H}{J}\right) S_{ij},\] kar računamo pri stari, še nespremenjeni mreži, hkrati pa premik v bližnjo okolico razumemo v smislu periodične mreže \(i \pm 1 \mathop{\mathrm{mod}} m\), pri čemer je \(m\) dimenzija mreže za indeks \(i\). Podobno je indeks \(j\) periodičen za dimenzijo \(n\).

4. Predlagano potezo sprejmemo tudi v primeru, da je \(\Delta \mathcal{E} > 0\), a le z verjetnostjo \(P_\mathrm{sprejetja} = e^{-\Delta \mathcal{E} / T}\) (tu uporabljamo brezdimenzijsko temperaturo, glej 2.1).

5. Naslednji korak. Ponovimo korak 2.

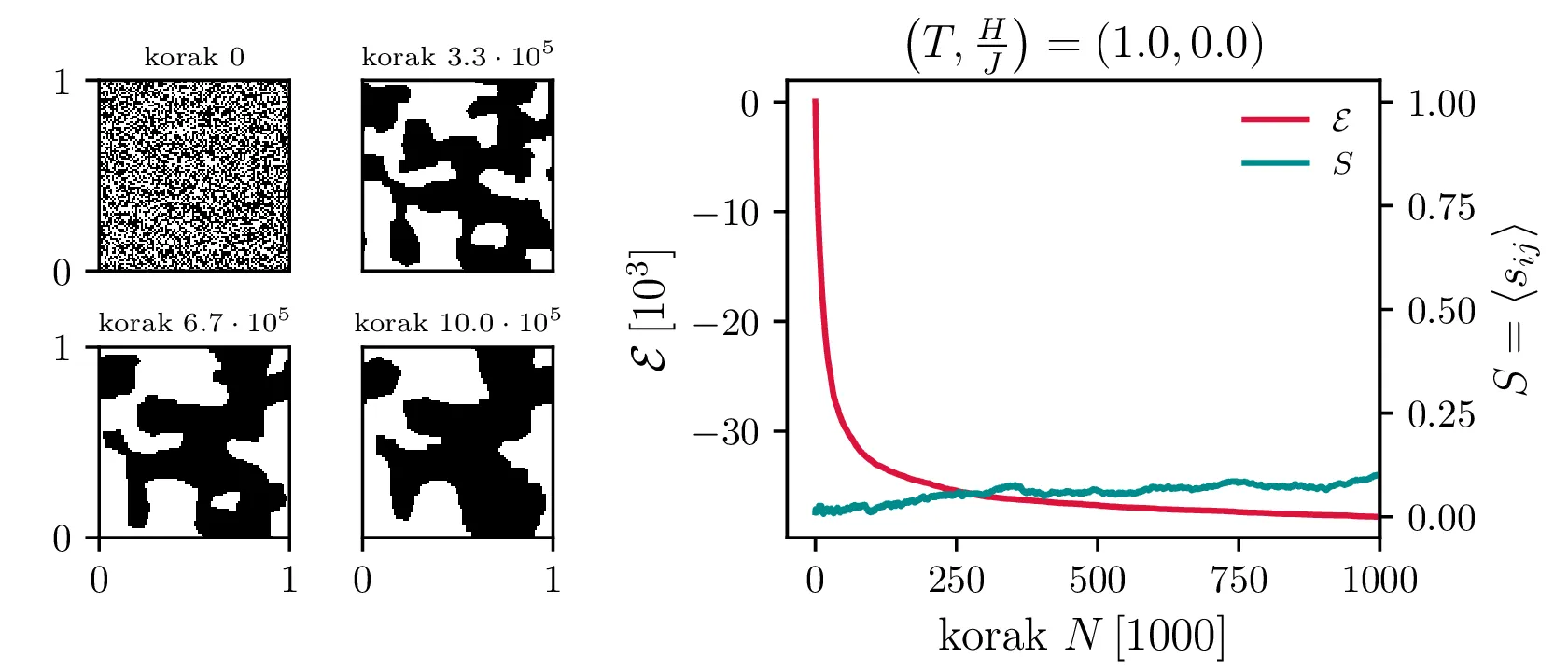
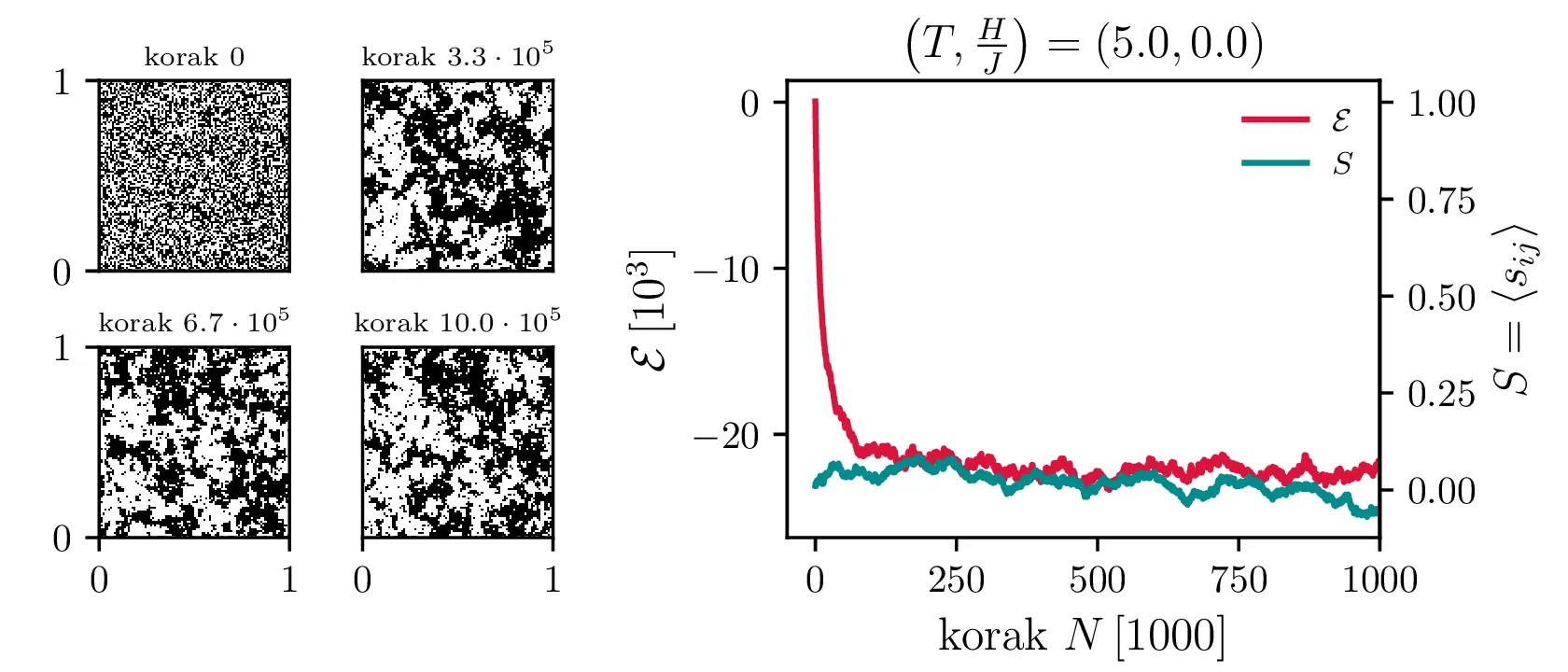
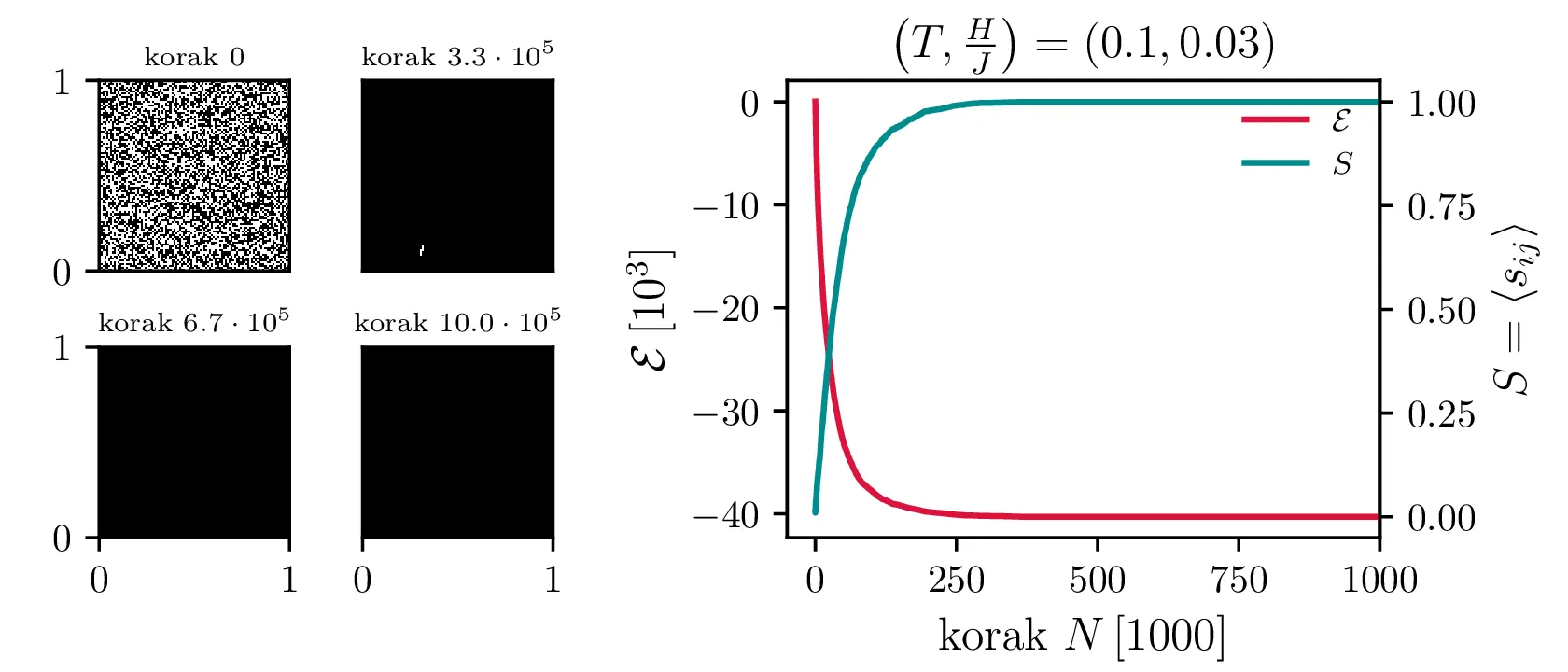
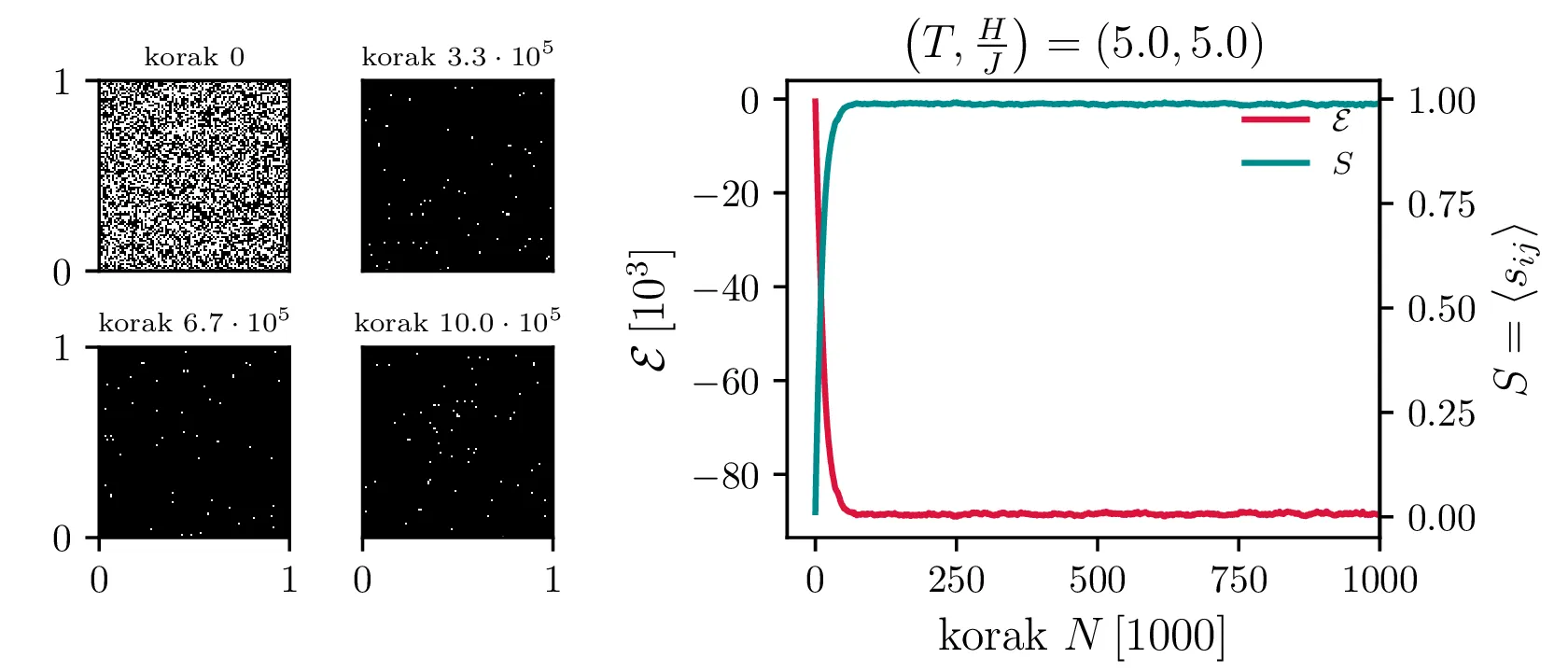
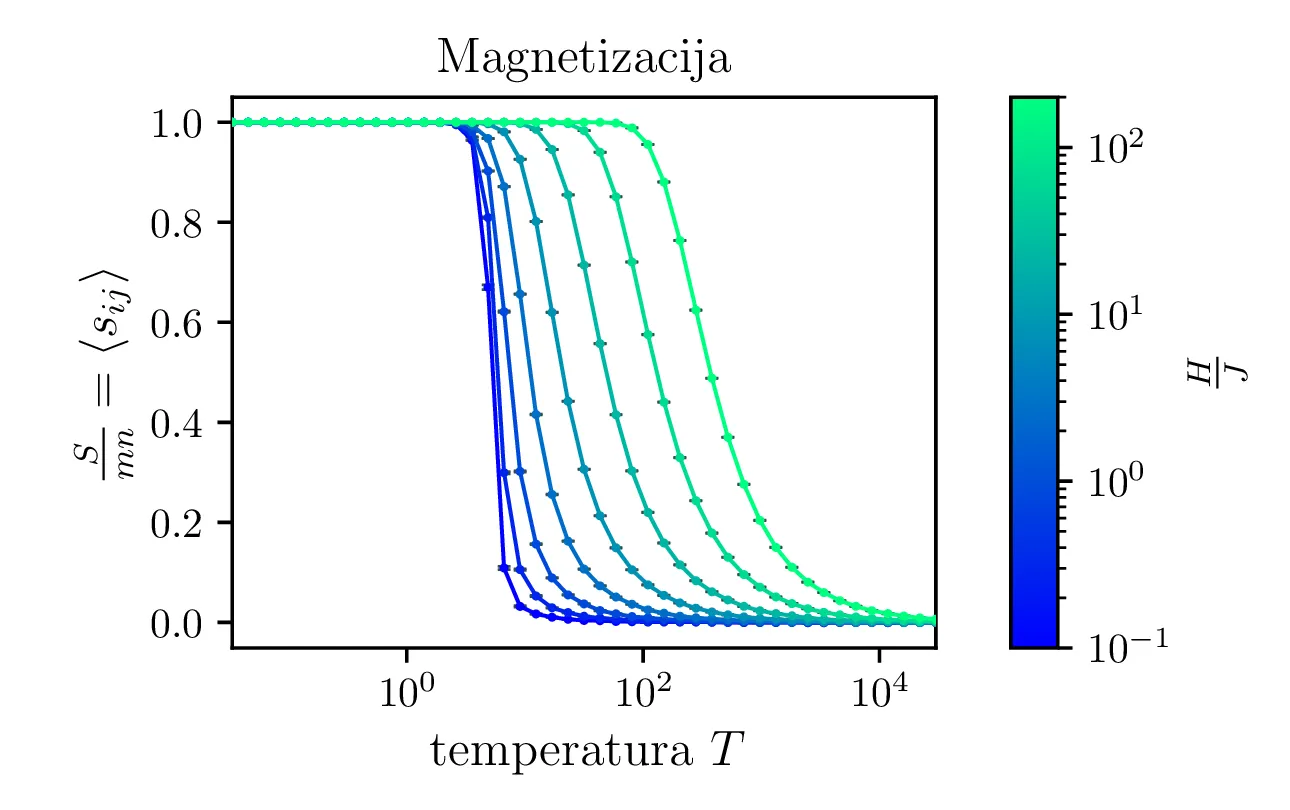
Po tem postopku si hitro pogledamo nekaj integracij. Na sliki 7 vidimo termalizacijo integracije za model \(100\times 100\), za nizko temperaturo \(T = 1\) in visoko (\(> T_c\)) temperaturi \(T = 5\). Pri nizki temperaturi se izoblikujejo magnetne domene, pri visoki pa je stanje nekakšen šum.

Specifična toplota

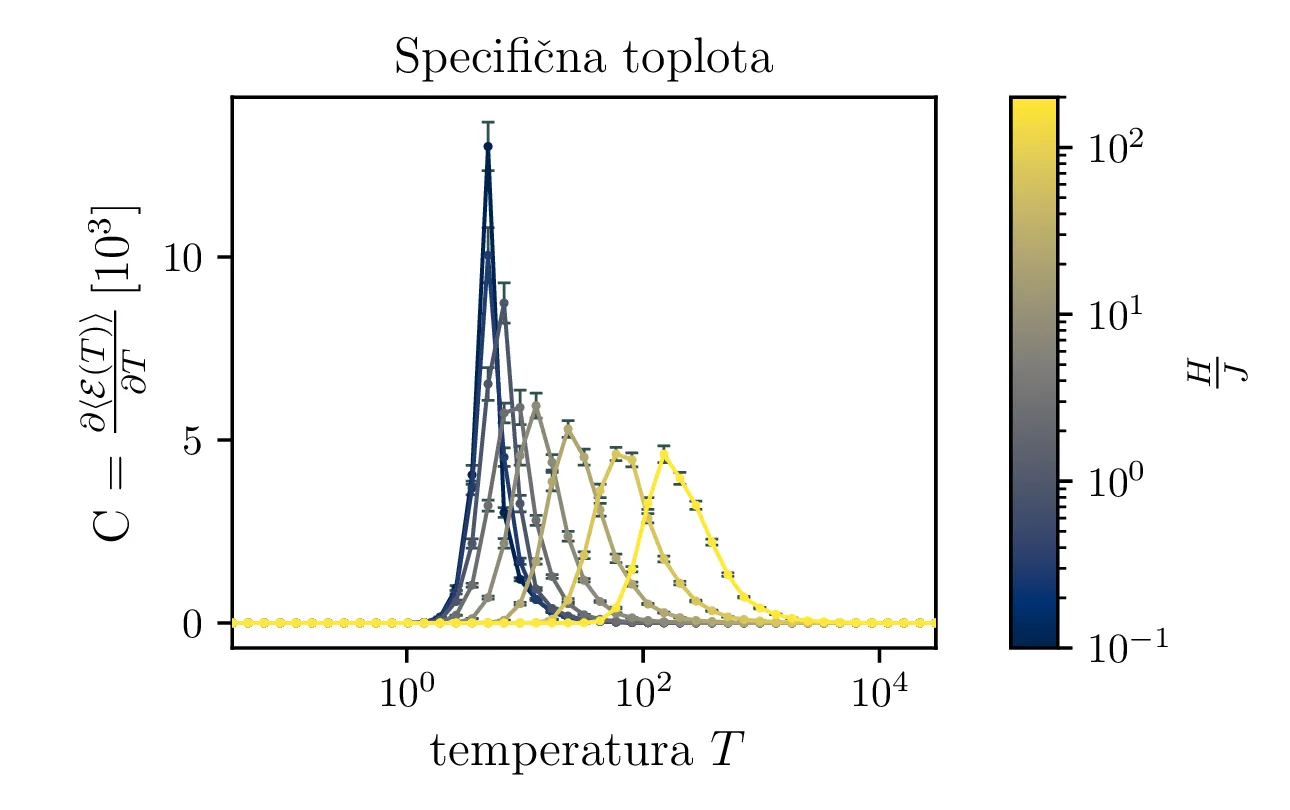
Na sliki 8 levo vidimo temperaturne odvisnosti energije Isingovega modela. Za močnejša zunanja polja je značilna višja temperatura energijskega prehoda, pri kateri sistem "kristalizira" v osnovno stanje z najnižjo možno energijo, kjer so vsi spini orientirani v isto smer \[\mathcal{E}_\mathrm{min} = mn \left( \frac{H}{J} + 4 \right).\] Za Isingov model lahko specifično toploto izračunamo popolnoma analogno kot za molekularno verižico v 2.4, torej kot \(C = \frac{\mathop{\mathrm{Var}}[\mathcal{E}]}{T^2}\), pri čemer standardno napako izračunamo preko 20 neprekrivajočih batch-ov. Tako izračunano specifično toploto vidimo na sliki 8 desno.

Magnetna susceptibilnost

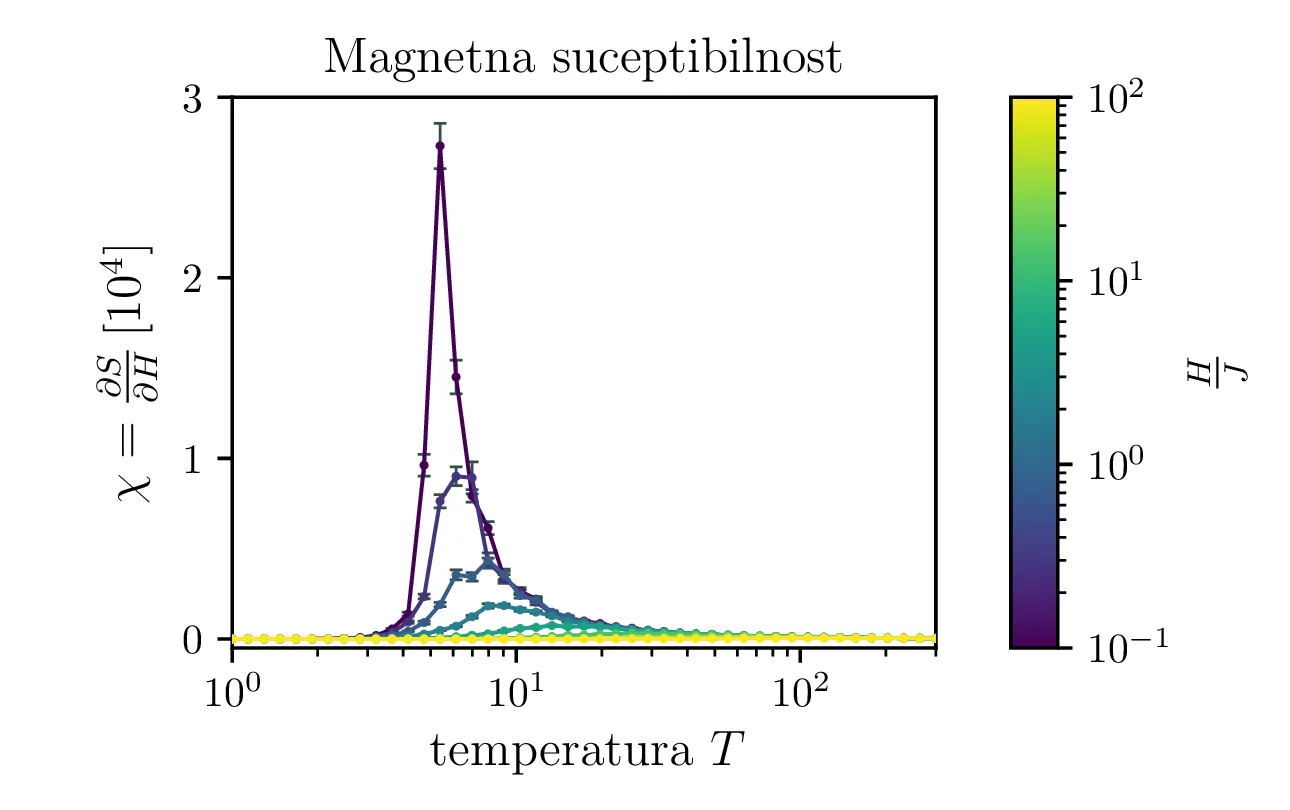
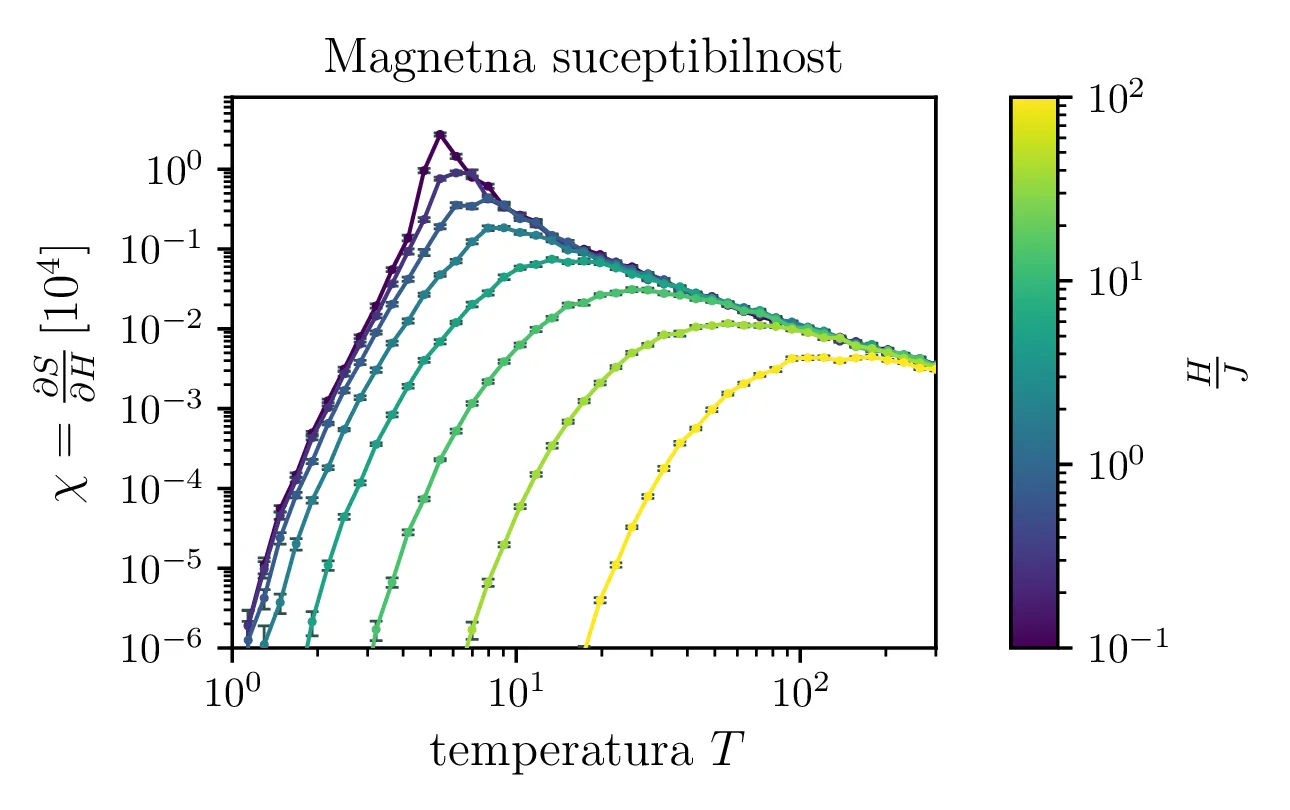
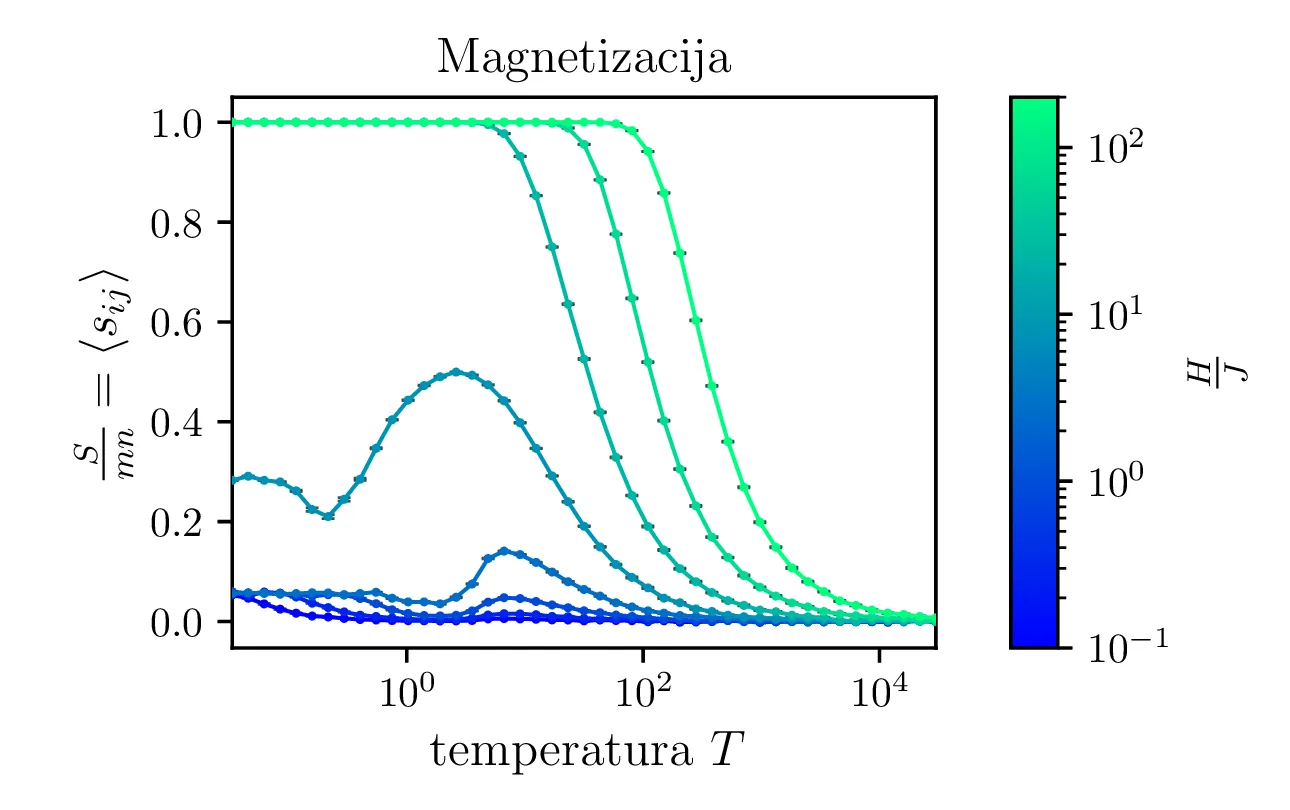
Podobno kot je specifična toplota odvod pričakovane energije \(C = \frac{\partial \langle \mathcal{E} \rangle}{\partial T}\), je magnetna susceptibilnost odvod magnetizacije (pričakovane vrednosti \(S = mn \langle s_{ij} \rangle\)) \[\chi = \frac{\partial S}{\partial H}.\] Tako lahko po zelo podobnemu argumentu kot tisti v 2.4 zaključimo, da je \[\chi = \frac{\mathop{\mathrm{Var}}\left[\sum_{ij} s_{ij}\right]}{T},\] pri čemer uporabljamo brezdimenzijsko temperaturo (glej 2.1). Na sliki 10 vidimo magnetizacijo in njene skoke s padanjem temperature. Pripadajoče temu vidimo na sliki 11 izračunano susceptibilnost, ki ima zelo visok vrh za majhna polja, ko je feromagnet še daleč od zasičenja. To se ujema z resničnim obnašanjem feromagnetov.

Histereza

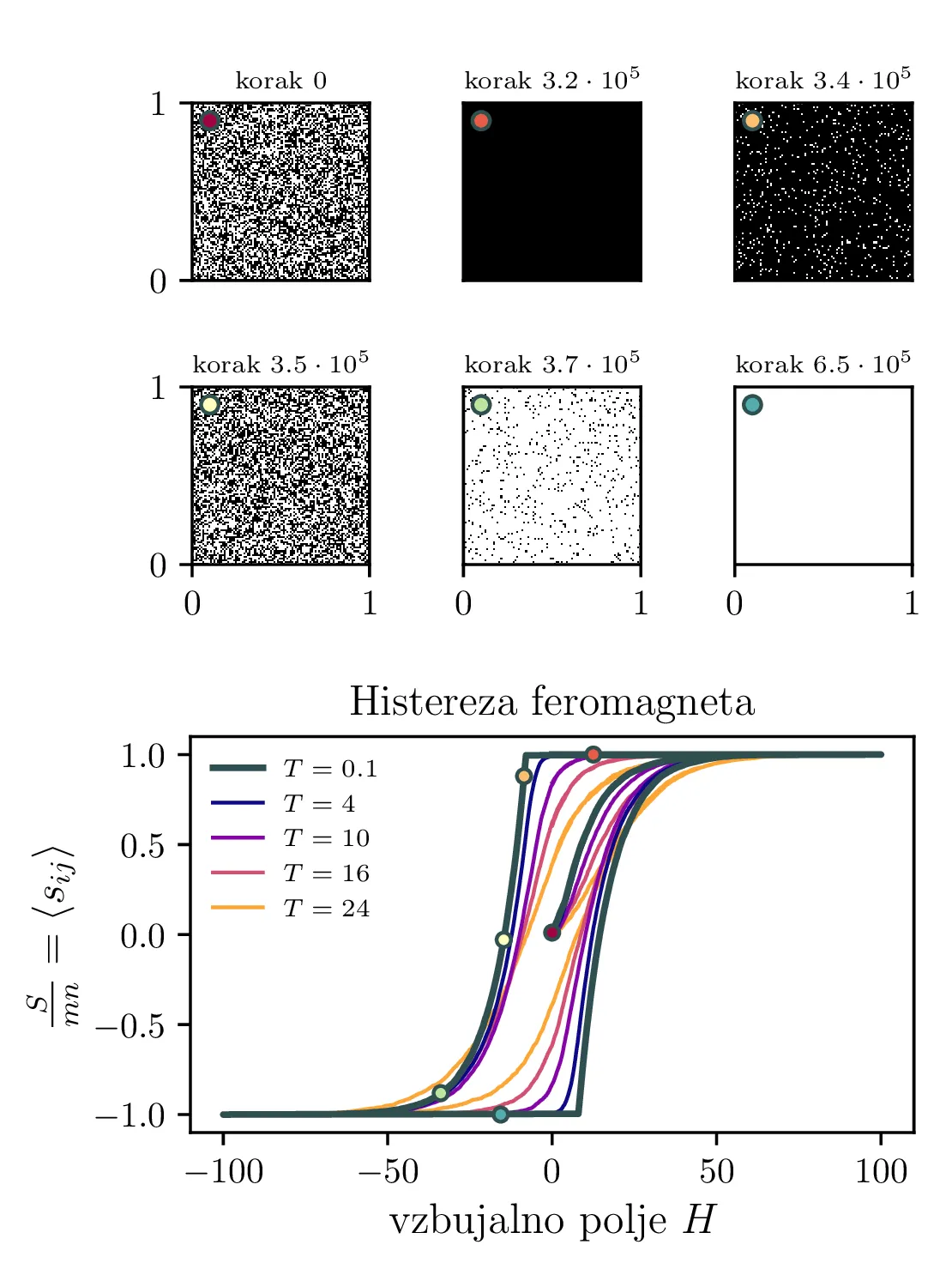
Še eno zanimivo fizikalno obnašanje feromagnetnih materialov je histereza magnetizacije pri spreminjanju vzbujalnega polja \(H_t\) po času \(t\). Tedaj krivulja \(t \mapsto (H_t, S(H_t))\) ne opisuje grafa neke funkcije \(S(H)\), temveč je bolj kompleksna, ciklična krivulja (glej sliko 12 spodaj). Histerezno obnašanje lahko relativno enostavno opazimo v Isingovem modelu, če le vstavimo časovno spreminjajoče polje \[H_t = H(T) = H_0 \cos({3\cdot 2\pi t/N}).\] Na sliki 12 vidimo obnašanje Isingovega \(100\times 100\) modela za \(H_0 = 100\), vključno z vmesnimi mikrostanji, ki lepo ilustrirajo celoten histerezni cikel. Začnemo v točki \((H, S) = (0, 0)\), kjer je sistem naključno urejen. Nato se s povečevanjem vzbujalnega polja \(H\) sistem povsem uredi v tej \(+1\) smeri. Da to urejenost podremo in sistem uredimo spet v drugo smer negativnega polja \(-1\), mora \(H\) polje postati znatno negativno. Tako torej samo urejeno \(\pm 1\) stanje sistema deluje kot spomin tega, kakšen je bil \(H\) ob prejšnjih časih.

Autokorelacija kot indikator za fazni prehod

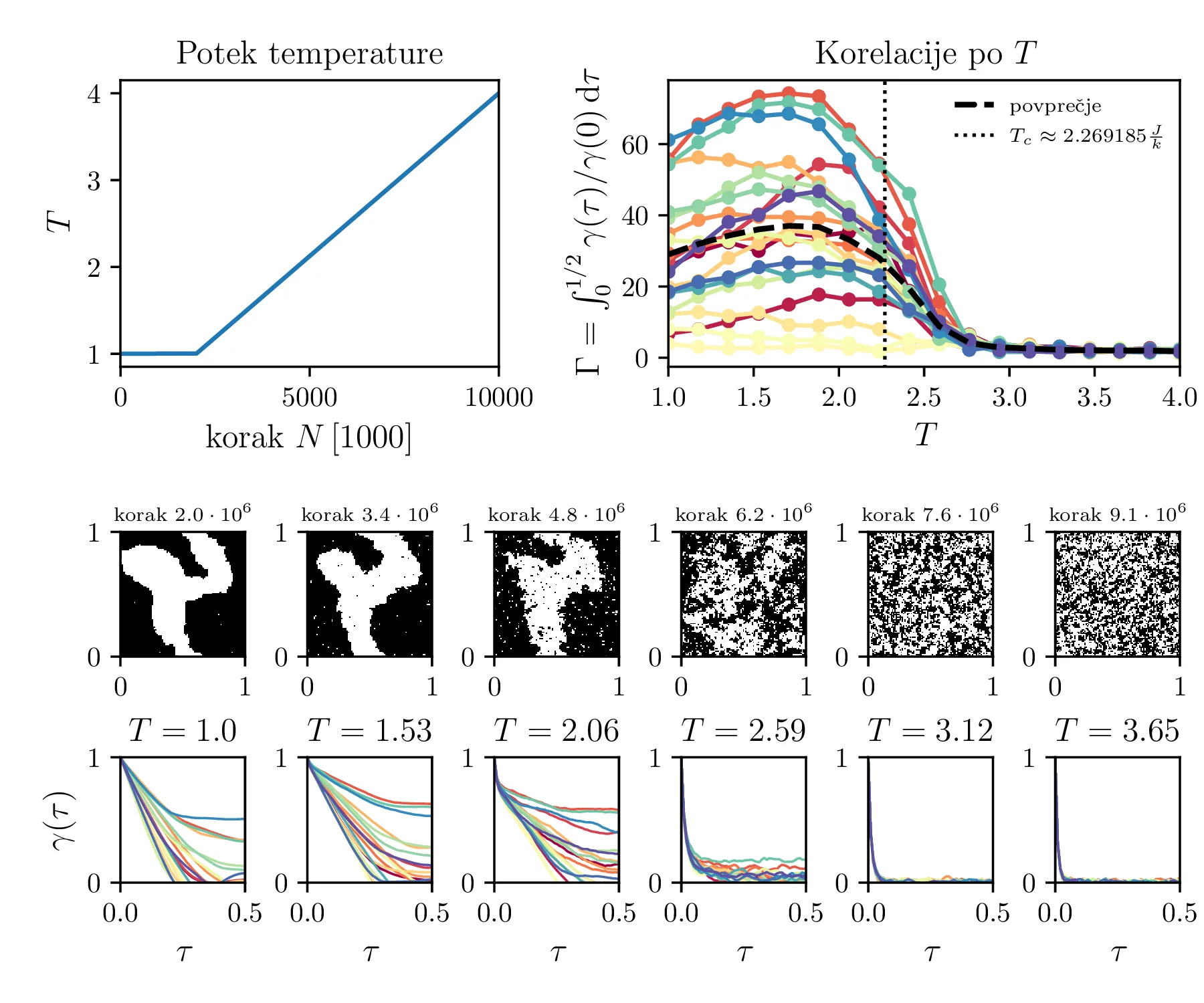
Preko autokorelacije sem poskusil kvantificirati fazni prehod, ki se pri Isingovem modelu po analitični napovedi pojavi pri \(T_c \approx 2.269185 \frac{J}{k}\). V ta namen sem Metropolis algoritem pognal z spremenljivo temperaturo \(T(t)\) (glej sliko 13 zgoraj levo). Nato sem iz celotnega poteka vzorčil 18 stanj pri različnih \(T\) in za njih izračunal \(\gamma(\tau)\) normirane autokorelacije v \(x\)-smereh. Šest izmed teh 18 stanj in njihove normirane \(\gamma(\tau)\) vidimo na sliki 13 spodaj. Kot indikator razdalje autokorelacij sem vzel kar njen integral \(\Gamma(T) \vcentcolon=\int_0^{1/2} \frac{\gamma(\tau)}{\gamma(0)} \,\mathrm{d}\tau\). Nato sem odvisnost \(\Gamma(T)\) narisal na sliki 13, sicer sem to ponovil za \(20\) simulacij dolgih po \(N = 10^7\) korakov. Te odvisnosti \(\Gamma(T)\) imajo pričakovan padec ko višamo temperaturo in magnetne domene nizkotemperaturne faze izginejo.

Antiferomagnet

Še en model realnih snovi, ki jih najdemo v naravi, a se jim v tej nalogi nisem posebej posvečal, so t. i. antiferomagneti. Opisuje jih povsem enak Hamiltonian kot 1, le da z dodatnim \(-1\) predznakom pred interakcijskim členom \(\sum_{\langle ij \rangle} s_i s_j\). Tak material se v odsotnosti polja organizira v šahovnico, oz. bolj natančno v večje domene nasprotno predznačenih šahovnic (glej 14). V limiti močnega polja se tako kot pri feromagnetu vsi spini uredijo v smer zunanjega polja. A pri manjših poljih pa je odziv nekoliko drugačen, kot vidimo na sliki 15.

Viri