Modelska analiza I
7. naloga: Naključna števila in integracije z metodo Monte Carlo

Navodila

Telesu, ki ga omejuje ploskev \[\sqrt{x} + \sqrt{y} + \sqrt{z} = 1,\] določi maso ter vztrajnostni moment: (a) če je gostota konstantna, (b) če se gostota spreminja z razdaljo od središča kot \(\rho = r^p\), kjer je \(r\) razdalja od središča telesa. Kakšen učinek ima vrednost parametra \(p\)? Oceni natančnost rezultatov. Opazuješ lahko tudi obnašanje ostalih momentov (težišče, povprečja sferičnih harmonikov).
V krogli se rojevajo žarki gama. Njihova povprečna prosta pot v snovi, iz katere je krogla, je enaka radiju krogle. Kolikšen delež fotonov uide iz krogle? Kako se verjetnost pobega spreminja z razmerjem povprečne proste poti in radija krogle?
Model nevtronskega reflektorja: tok nevtronov vpada pravokotno na ploščo, v kateri se nevtroni sipljejo in nič ne absorbirajo, pri čemer je njihova prosta pot enaka polovici debeline plošče. V poenostavljenem modelu privzamemo, da se sipljejo samo naprej in nazaj, in to z enako verjetnostjo. Kakšna je porazdelitev po številu sipanj? Kolikšna je prepustnost reflektorja? Oceni natančnost. Nekoliko bolj realen je model z izotropnim sipanjem. Z njim preveri, koliko so rezultati poenostavljenega modela uporabni. Razišči še kotno porazdelitev odbitih in prepuščenih nevtronov ter odvisnost prepustnosti od debeline plošče v modelu z izotropnim sipanjem

(Levo) Ilustracija geometrijskega telesa, omejenega s ploskvijo \(\sqrt{|x|} + \sqrt{|y|} + \sqrt{|z|} = 1\). (Desno) Zgornji desni kvadrant lika \(\sqrt{|x|} + \sqrt{|y|} < 1\) (senčeno zeleno) in prikaz točk, generiranih direktno v trikotniku (glej razdelek 2.1.1).

Volumen geometrijskega telesa

2-dimenzijski presek

Še pred volumnom 3-dimenzijskega telesa si bomo pogledali še nekoliko preprostejši primer telesa opisanega kot \[\sqrt{|x|} + \sqrt{|y|} < 1.\] To telo je pravzaprav 2-dimenzijski presek telesa, ki ga bomo gledali v nadaljevanju. Površina takega lika je izražen kot integral \[S = \int_0^1 \left( 1 - \sqrt{x} \right)^2 \,\mathrm{d}x = \frac{1}{6}.\]

Integracija za lik \(\sqrt{|x|} + \sqrt{|y|} < 1\) in primerjava med različnimi načini generiranja točk in različnimi načini računanja variance. (Levo) V barvah je narisan potek MC integracije za ansambel 100 integracij po \(10^5\) korakov. Točke generiramo v trikotniku kot opisano v sekciji 2.1.1. Temno modro je narisano ansambelsko povprečje za 100 integracij, roza pa ansambelsko povprečje za 100 integracij po domeni \([0, 1]^2\) namesto po trikotniku. (Sredinsko) Napake za posamezne potke integracije, odstopanje ansambelskega povprečja (temno modro) in \(\hat\sigma\) razpršenosti za ansambel pri integraciji po trikotniku (vijolično) in pri integraciji po kvadratu \([0, 1]^2\) (rožnato). Na manjšem grafu levo stopaj je narisano tudi razmerje teh dveh razpršenosti, za katerega bi pričakovali, da je \(\sim 0.5\). (Desno) Drugačen način računanja variance za le en \(10^7\) dolg potek integracije, kjer gledamo namesto razpršenosti ansambla razpršenost \(\sqrt{\langle S^2 \rangle - \langle S \rangle^2}\).

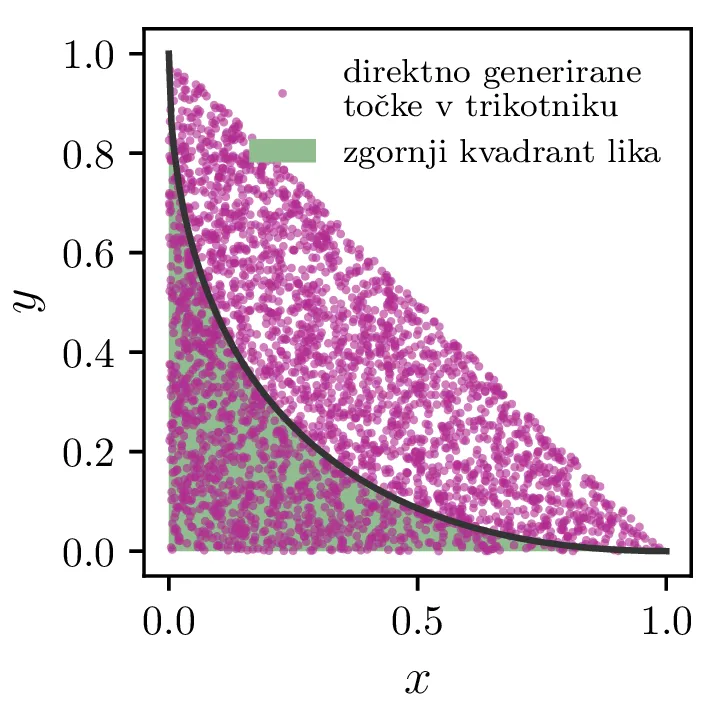
Generiranje točk na trikotniku

Ker je zgornji desni kvadrant lika \(\sqrt{|x|} + \sqrt{|y|} \le 1\) povsem vsebovan v trikotniku \((0, 0), (1, 0), (0, 1)\), lahko to izkoristimo in prihranimo \(1/2\) poskusov tako da direktno generiramo točke znotraj tega trikotnika. To storimo tako, da uporabimo baricentrične kordinate in generiramo števila \[\alpha \sim U(0, 1), \qquad \beta \sim U(0, 1),\] nato pa enakomerno porazdeljene točke znotraj trikotnika \((0, 0), (1, 0), (0, 1)\) dobimo kot \[\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \alpha & (\beta - \alpha) & 1 - \beta \end{bmatrix} \begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{bmatrix}\] Primer takega vzorčenja vidimo na sliki 1 desno.

Ocena napake

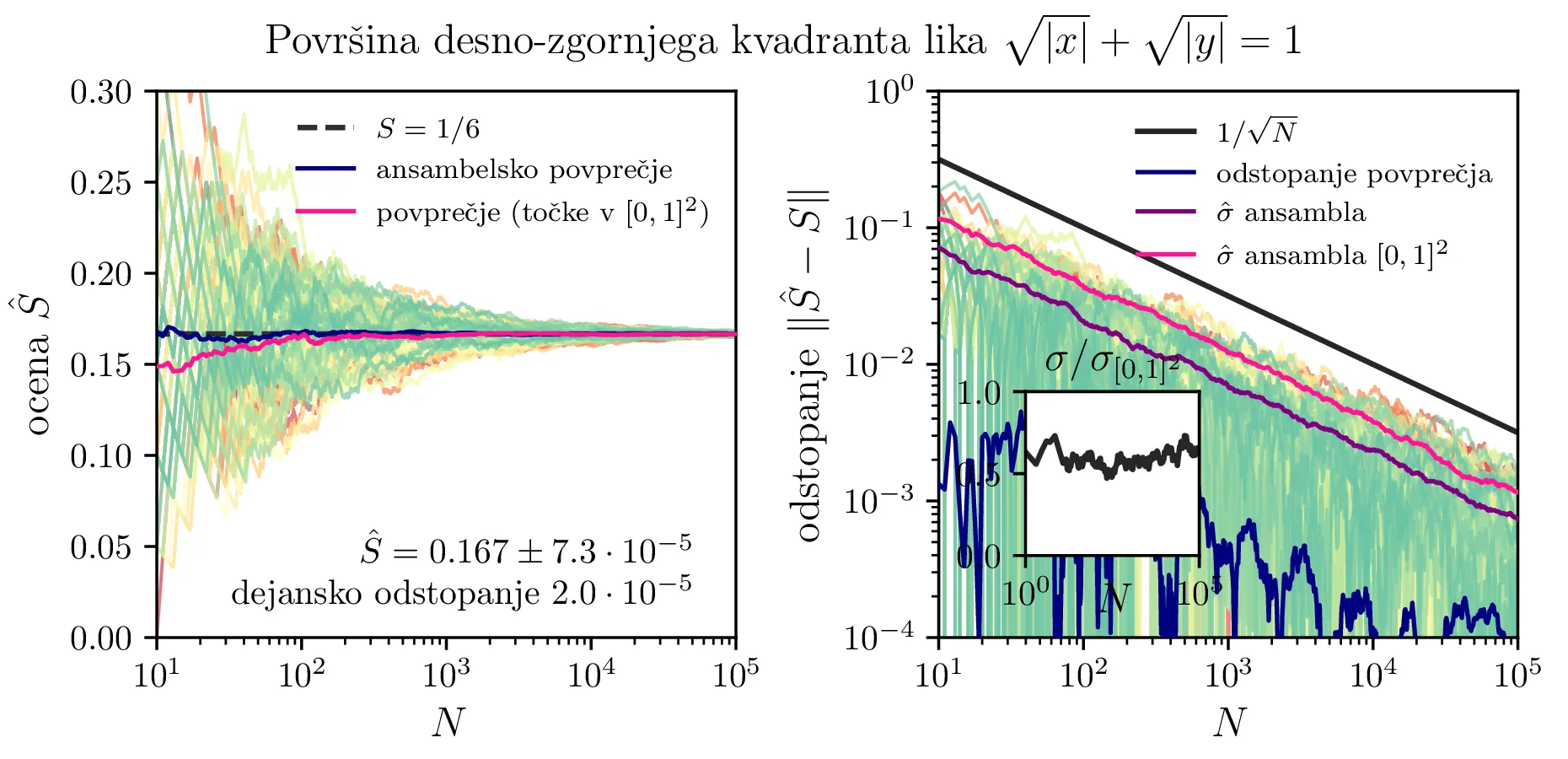
(Levo) Volumni za potek ansambla \(M = 100\) integracij po \(10^6\) korakov. (Desno) Napaka takih integracij, ki pada kot \(\frac{1}{\sqrt{N}}\). Vidimo, da je ansambelska standardna napaka \(\mathrm{SE} = \frac{\hat\sigma}{\sqrt{M}}\) (svetlejša modra črta) dobra ocena za napako ansambelskega povprečja (temno modra črta).

Za površino lika \(\sqrt{|x|} + \sqrt{|y|} < 1\), v nadaljevanju pa tudi za volumen telesa \(\sqrt{|x|} + \sqrt{|y|} + \sqrt{|z|} < 1\), lahko izračunamo eksakten rezultat, ki nam omogoča preprosto vrednotenje napake MC integracije. V dejanskih aplikacijah MC integracije, kjer eksakten rezultat ni na voljo, pa vseeno potrebujemo nek način za oceno napake.

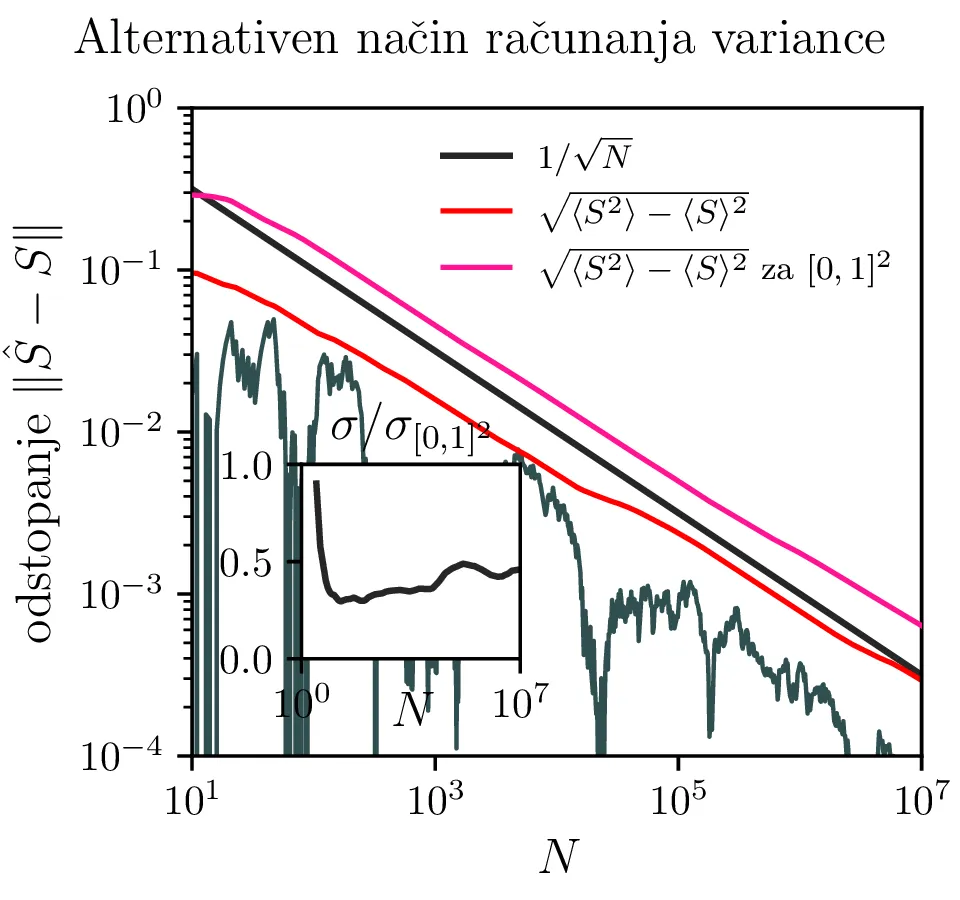
Najbolj intuitiven način za oceno se mi zdi kar standardna napaka ansambla, kjer poženemo ansambel \(M\) integracij, za katere dobimo rezultate \([S_i]_{i=1}^M\), nato pa rezultat z napako podamo kot \begin{equation}S = \langle [S_i]_{i=1}^M \rangle \pm \frac{\hat{\sigma}_{[S_i]_{i=1}^M}}{\sqrt{M}}. \label{eq:format}\end{equation} Takšna napaka je t. i. standardna napaka (ang. standard error ali SE), ki ocenjuje standardno deviacijo vzorčnega povprečja. Na sliki 2 sredinsko npr. vidimo tako oceno \(\hat\sigma\) za ansambel velikosti \(M = 100\), in iz logaritemske skale je razvidno, da po deljenju z \(\sqrt{100}\) to ustreza tudi velikosti napake \(\langle [S_i]_{i=1}^{100} \rangle\) (ta je narisana v temno modri barvi). Alternativa ansambelskemu načinu računanja in oceni napake je znana formula za varianco \[\mathop{\mathrm{Var}}(S) = \langle S^2 \rangle - \langle S \rangle^2.\] Če uporabimo to formulo, lahko napako ocenimo tudi brez ansambla večjih integracij. Iz poskusov (glej sliko 2 desno) sem ugotovil, da je potek takšne napake sicer na izgled bolj gladek, je pa bolj nestabilen od ansambelske SE napake. V nadaljevanju torej uporabljam ansambelsko SE napako in rezultate navajam v obliki (1). Da je napaka \(\mathrm{SE}\) res primerna za oceno napake ansambelskega povprečja, lahko jasno vidimo tudi na sliki 3 desno.

Volumen in vztrajnostni moment lika

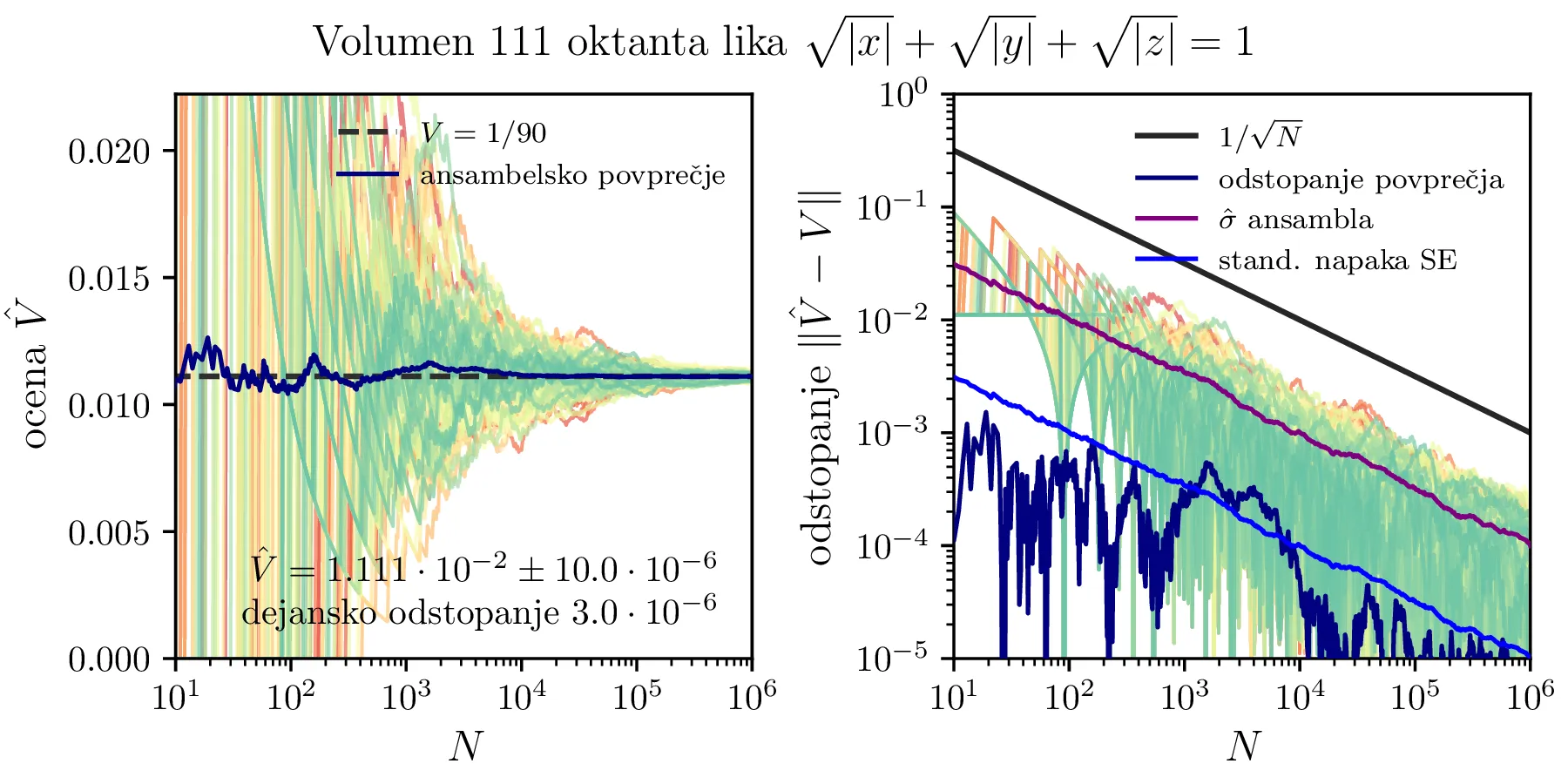
Izračunati želimo volumen telesa \[\sqrt{|x|} + \sqrt{|y|} + \sqrt{|z|} < 1,\] konkretno nas bo zanimala \(1/8\) tega volumna, torej volumen v \(111\) oktantu. Volumen enega takega oktanta je \[V = \int_0^1 \int_0^{(1 - \sqrt{y})^2} \big(1 - \sqrt{x} - \sqrt{y}\big)^2 \,\mathrm{d}x \,\mathrm{d}y = \frac{1}{90}.\] Na sliki 3 vidimo integracijo \(100\times10^6\), t. j. ansambel 100 integracij po \(10^6\) korakov. Tako izračunamo za volumen enega oktanta \[\hat{V} = 1.111 \cdot 10^{-2} \pm 10^{-7},\] kar znotraj \(\mathrm{SE}\) napake ustrezno in se ujema z \(V = 1/90\), dejansko odstopanje je \(3\cdot10^{-6}\). Samo integracijo lahko nekoliko posplošimo z uvedbo gostote \begin{equation}\rho = (p+1) r^{p}, \label{eq:rho}\end{equation}

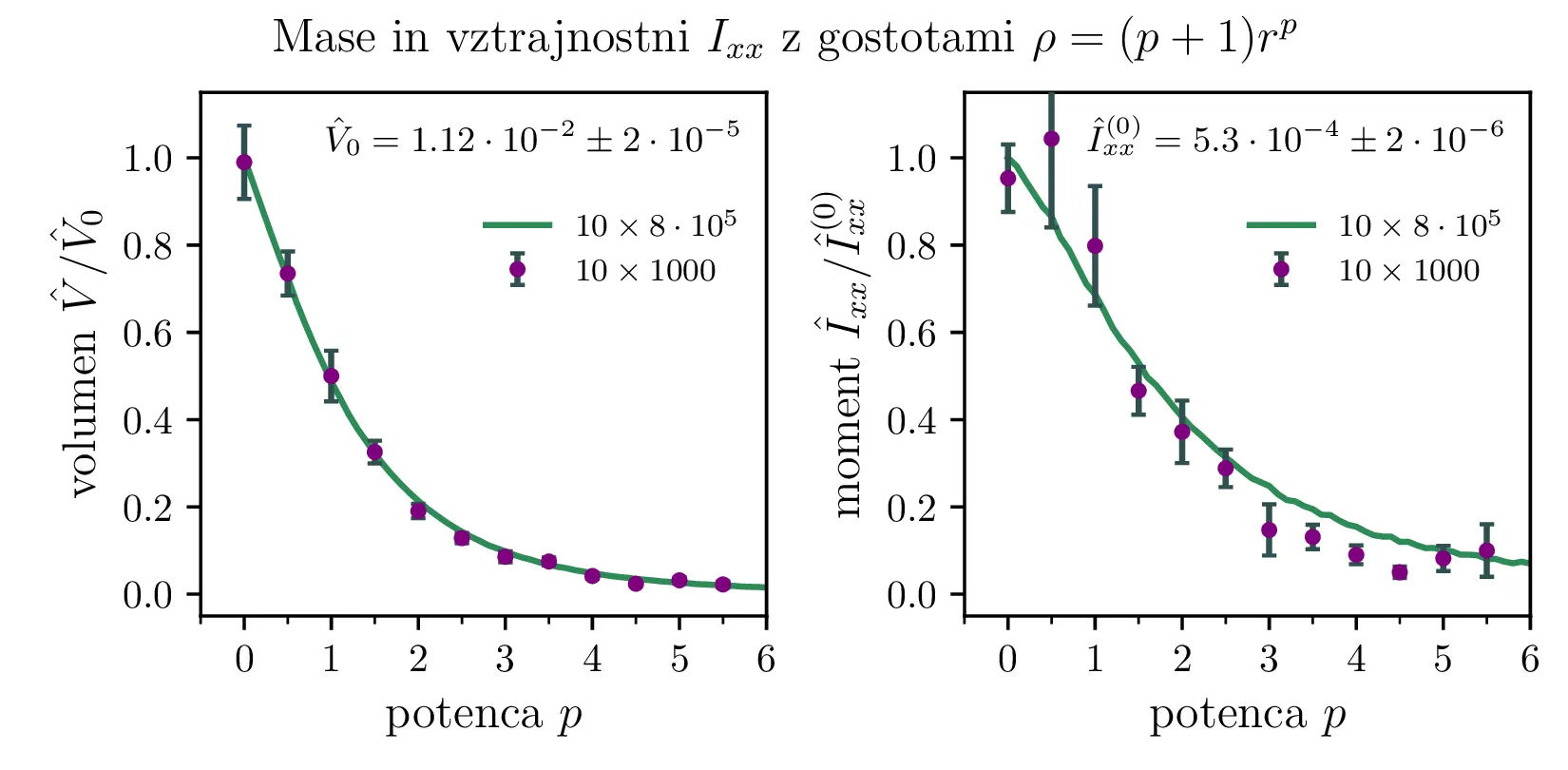
Razmerja izračunanih mas (Levo) in vztrajnostnih momentov (Desno) za manjši ansambel \(10\times 1000\) in za večji ansambel \(10\times 8\cdot 10^5\). Iz približno \(1/3\) ujemanj znotraj napake med manjšim in večjim ansamblom lahko zaključimo, da je tak način ocenjevanja napake smiseln.

s katero moramo pri vsoti obtežiti posamezne točke v integraciji. Na sliki 4 levo vidimo odvisnost volumna od potence v gostoti (2). Poleg mase lahko izračunamo tudi vztrajnostni moment \[I_{xx} = \frac{1}{8} \iiint_{\sqrt{|x|} + \sqrt{|y|} + \sqrt{|z|} < 1} \rho(x, y, z) (y^2 + z^2) \,\mathrm{d}x \,\mathrm{d}y \,\mathrm{d}z.\] Tako definiran vztrajnostni moment okoli \(x\)-osi vidimo na sliki 4, izračunan za različne eksponente \(p\). Vidimo, da je račun take količine precej bolj zašumljen kot izračun mase.

Importance sampling

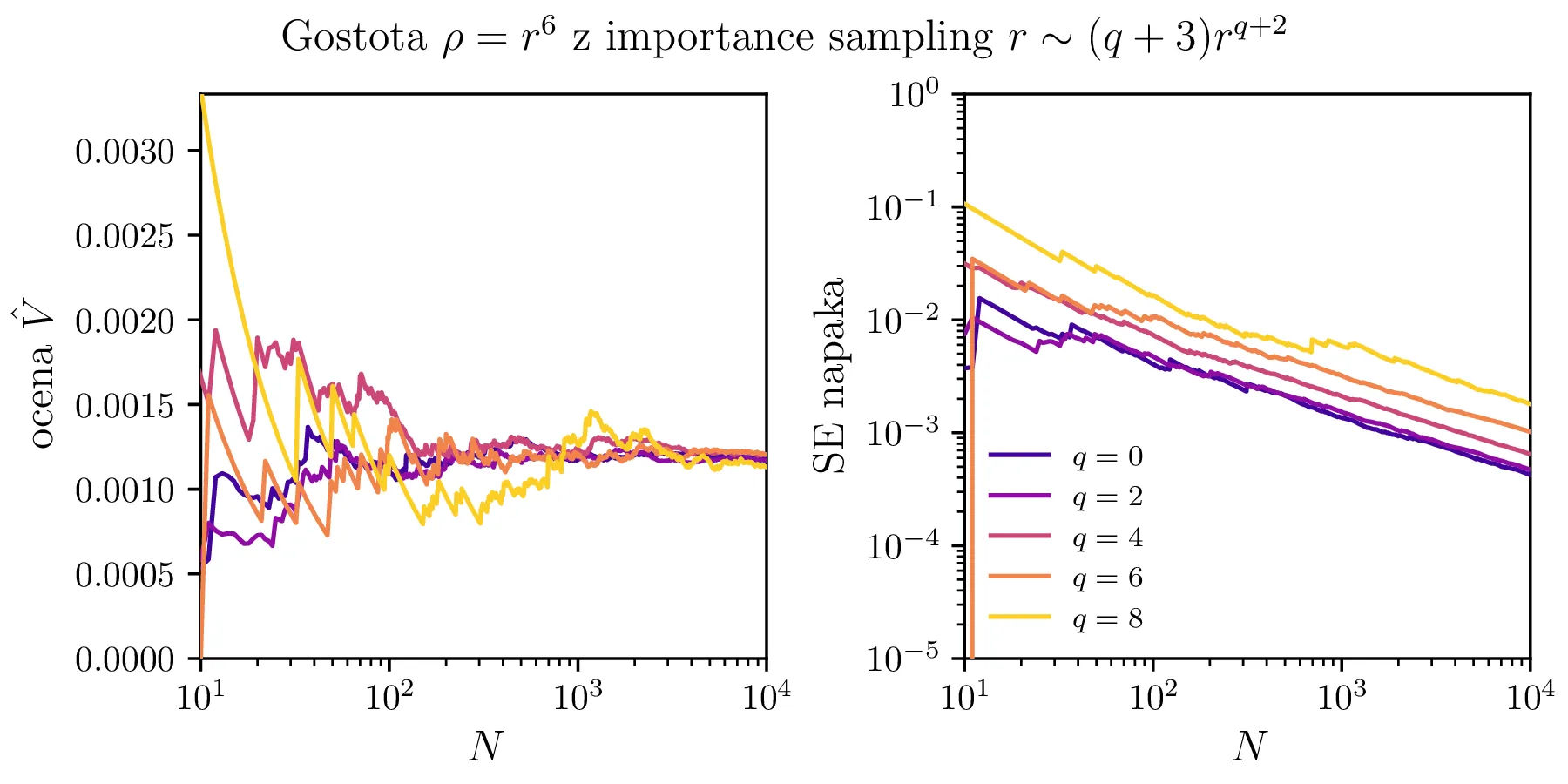
Ker gostota našega telesa (2) zdaj narašča z \(r\), se nam porodi misel, da bi integral gosteje vzorčili pri večjih \(r\). To lahko realiziramo s t. i. pomembnostnim vzorčenjem (ang. Importance sampling), kjer vzorce porazdelimo neenakomerno, sorazmerno s tem pa jih tam kjer je vzorčenje redkejše, močneje obtežimo. Zahtevamo, da je ta porazdelitev neničelna povsod,kjer je \(F(X) \neq 0\). Nato MC integracija neke količine \(F(X)\) za naključno spremenljivko \(X \sim g\) poteka kot

Generiraj vzorce iz nove porazdelitve \(Y_i \sim h\) za \(i = 1, 2, \dots, N\).
Izračunaj pričakovano vrednost \(\langle F(X) \rangle\) kot obteženo vsoto \[\langle F \rangle \approx \frac{1}{N} \sum_{i = 0}^N w(Y_i) F(Y_i)\] pri čemer so vzorci iz nove porazdelitve \(h\) obteženi kot \[w(Y_i) = \frac{g(Y_i)}{h(Y_i)}.\]

Ko generiramo naključno porazdeljene točke v volumnu enotske krogle, izberemo za radij \[r \sim 3 r^2\] Da naredimo MC integracijo gostejšo pri večjih \(r\) (da proti bolj zunanjim lupinam gostota raste kot \(r^q\)), po novem žrebamo iz porazdelitve \[r \sim (q+3) r^{q+2} = \sqrt[q+2]{U(0, 1)}.\]

Verjetnost pobega iz krogle

(Levo) Skica krogle, v notranjosti katere nastajajo \(\gamma\)-fotoni. Zaradi sferične simetrije se lahko omejimo le na dogajanje na enemu radialnemu poltraku (črtkana črta). Foton nastane na nekem položaju v krogli, opisanim le z radialno koordinato \(R \sim \sqrt[3]{U(0, 1)}\). Sevanje fotonov je izotropno, ker pa je je problem simetričen tudi glede na preslikavo čez črtkano os, lahko gledamo le kote med \(0\) in \(\pi\). Absorbcijo fotona v snovi modeliramo z eksponentno porazdelitvijo "realizirane poti" \(\ell\), pri čemer je parameter porazdelitve \(\frac{1}{\lambda}\) enak povprečni prosti poti v tej snovi. Le če je \(\ell > L(R, \vartheta)\), bomo šteli, da je foton ušel iz krogle. (Desno) Odvisnosti razdalje \(L(R, \vartheta)\) od točke nastanka fotona do površine krogle.

Izračunati želimo verjetnost za pobeg \(\gamma\)-žarkov iz krogle, v kateri nastajajo na naključnih mestih, homogeno po volumnu. V snovi, iz katere je narejena krogla, se absorbirajo po eksponentni atenuaciji \(e^{-\lambda x}\), pri čemer je parameter povezan s povprečno prosto potjo fotona v snovi \[\frac{1}{\lambda} = \langle \ell \rangle.\]

Verjetnosti za pobeg \(\gamma\)-žarka iz krogle glede na povprečno prosto pot \(\langle \ell \rangle = \frac{1}{\lambda}\) oz. razmerje povprečne proste poti proti radiju krogle (ta je v računu fiksno enak \(1\)). Narisan je manjši \(10\) manjših integracij po \(50\) točk, povezane črte pa so bolj točna integracija \(10\times8\cdot10^3\).

(Levo) Verjetnosti za pobeg v logaritemski skali, itegracija z ansambli \(10\times8\cdot10^3\). Vidimo da je izračun problematičen za zelo majhne ali zelo velike \(\langle \ell \rangle\). Račun sem poskusil izboljšati z importance sampling po porazdelitvi za \(5\langle \ell \rangle\), z obtežitvijo kot opisano v 2.4. To integracije ni izboljšalo. (Desno) Primerjava MC integracije \(\hat{P}\) z hibridno metodo \(\widetilde{P}\), pri kateri azimutalni kot \(\vartheta\) sevanja (glej skico 6 levo) povzorčimo enakomerno, ne-naključno na intervalu \([0, \pi]\). Primerjavmo tudi integracijo z *importance sampling* vzorčenjem za \(5\)-kratni \(\langle \ell \rangle\). Vidimo da se izračuna ne ujemata povsem, varianca je za hibridno metodo pravzaprav še večja pri zelo majhnih \(\langle \ell \rangle\). Vzorčenje *importance sampling* je nepričakovano najslabša od vseh metod.

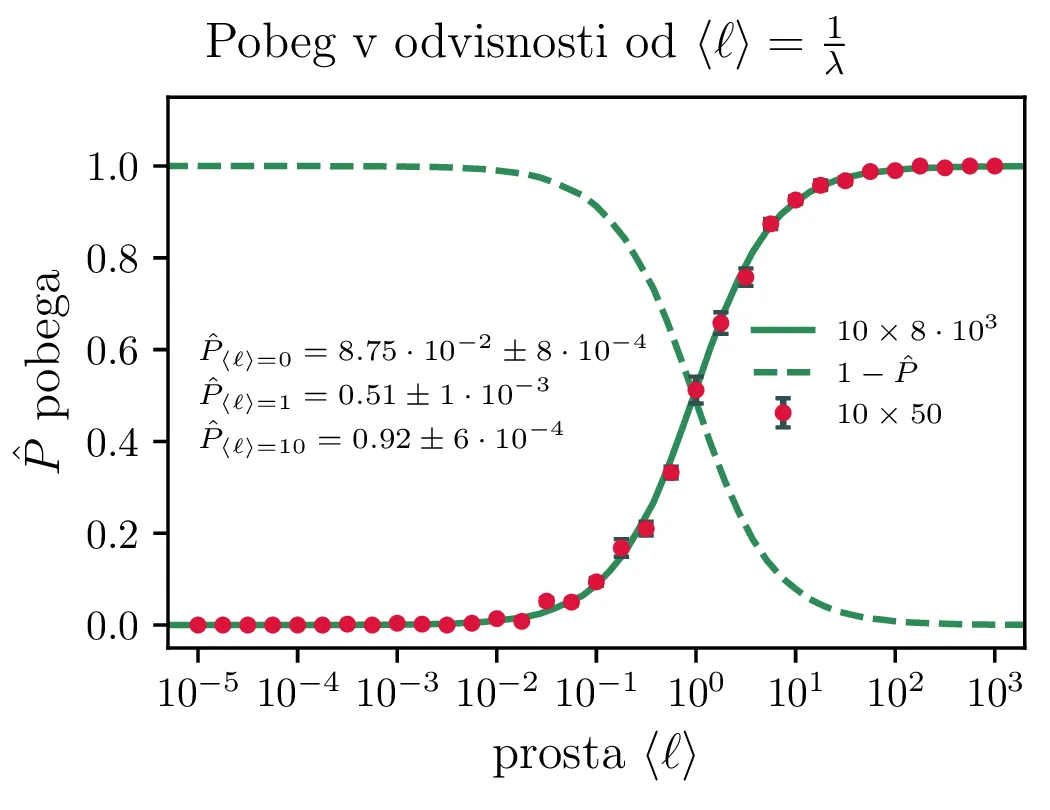
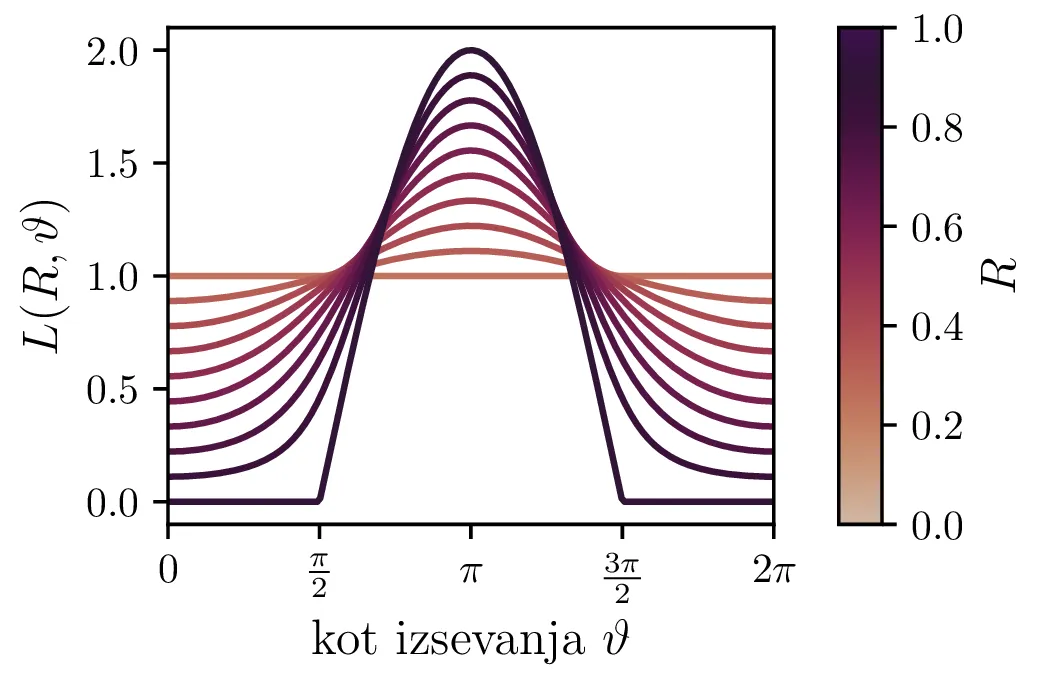
Ker bomo za kroglo izbrali enotsko kroglo, je brezdimenzijska tudi prosta pot \(\langle \ell \rangle\) in torej predstavlja razmerje med dejansko povprečno prosto potjo in radijem krogle. Ker je problem sferično simetričen, ga lahko gledamo le na enem radialnemu poltraku iz središča sfere (glej skico 6 levo). Na takem poltraku izberemo nek \(R \sim \sqrt[3]{U(0, 1)}\), nato pa še kot \(\vartheta \sim U(0, \pi)\), saj je nastajanje izotropno (vzamemo lahko le \([0, \pi]\), saj je druga polovica \([0, -\pi]\) povsem enakovredna). Mehanizem eksponentne absorbcije tedaj modeliramo tako, da za "dogodke" oz. fotone žrebamo neko "realizirano pot" \(\ell \sim \lambda e^{-\lambda x}\), nato pa preverimo, če je \(\ell\) dovoljšen, da foton uide iz krogle, če pot začne na poltraku pri \(r = R\) in potuje v smer \(\vartheta\) glede na izbrani poltrak. Če za tak poltrak vzamemo \(x\)-os, je potovanje izsevanega fotona omejeno na žarek \[\mathbf{r} = (R + S \cos\vartheta, S \sin\vartheta, 0), \quad S \in \mathbb{R}^+,\] pri čemer je \(S\) pot fotona po žarku v smeri, v katero je bil izsevan. Razdalja, ki jo mora prepotovati, da zapusti kroglo (razdalja do površine) je tedaj rešitev kvadratne enačbe \[R^2 + 2RS \cos\vartheta + S^2 = 1,\] in ustrezna pozitivna rešitev je razdalja do površine krogle \begin{equation}L(R, \vartheta) = -R \cos(\vartheta) + \sqrt{ \frac{2 - R^2 + R^2 \cos(2\vartheta)}{2} }. \label{eq:L}\end{equation} To odvisnost \(L(R, \vartheta)\) lahko vidimo na sliki 6 desno. Zdaj nam ostane le žrebanje točk \((R, \vartheta, \ell)\) in preverjanje \(\ell > L(R, \vartheta)\). Delež dogodkov, v katerih ta neenakost drži, se pri integraciji približuje verjetnosti za pobeg iz krogle. Tako izračunane verjetnosti za pobeg vidimo na sliki 7.

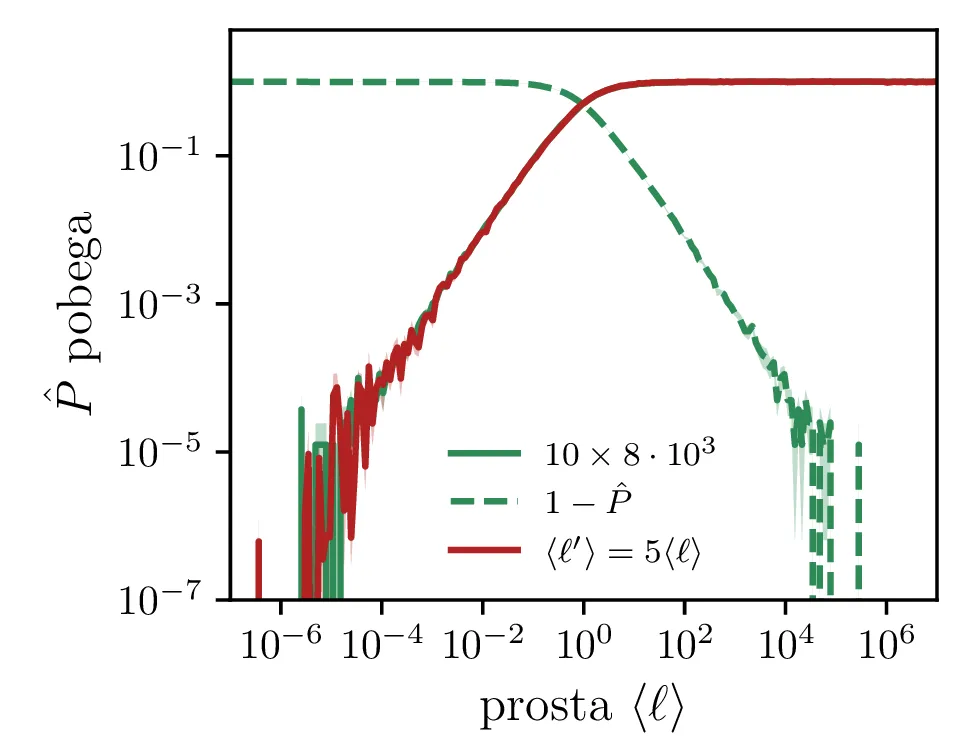
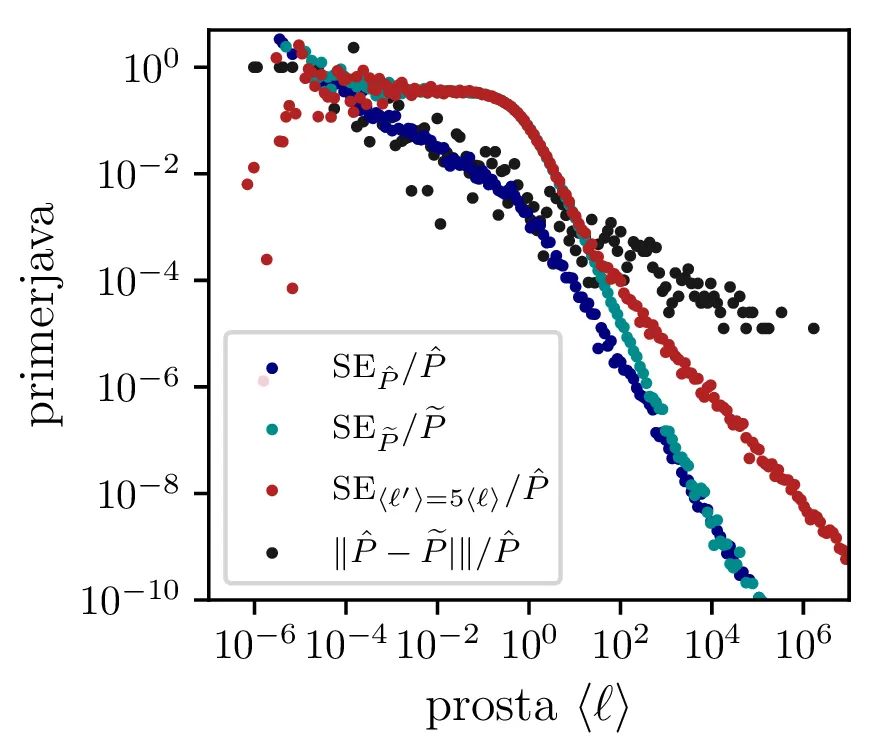
Napake za ekstremne vrednosti proste poti

Kot vidimo na sliki 8 levo, je MC integracija relativno nenatančna za zelo majhne ali zelo velike \(\langle \ell \rangle\). Tedaj je med končnim vzorcev dogodkov zelo malo dogodkov, kjer foton pobegne in statistični šum postane znaten. To sem poskusil rešiti tako, da sem realizirane poti \(\ell\) dejansko žrebal po porazdelitvi \(\sim \lambda' e^{-\lambda' x}\) za prosto pot \(\frac{1}{\lambda'} = \langle \ell' \rangle\), kjer smo za \(\langle \ell' \rangle\) izbrali 5-kratnik dejanske proste poti, za katero smo računali verjetnost pobega. Kot je vidno in opisano na sliki 8 ta procedura ni delovala, napaka se je kvečjemu poslabšala.

Hibridna metoda

Poleg povsem naključne MC metode z naključnimi spremenljivkami \((R, \vartheta, \ell)\) sem poskusil tudi hibridno metodo, kjer vzorci \(\vartheta\) niso zares naključni, temveč so enakomerno in ne-naključno porazdeljeni po \([0, \pi]\). Kot vidimo na sliki 8 desno, je tudi taka metoda slabša od navadne MC integracije.

Nevtronski reflektor

Poteki za \(N = 100\) delcev pri \(\langle \ell \rangle = 0.2\). Prikazane so tri različne debeline reflektorja \(d \in \{ 1, 2, 3 \}\) (Od leve proti desni). Opazimo, da je število prepuščenih nevtronov večje za tanjši reflektor.

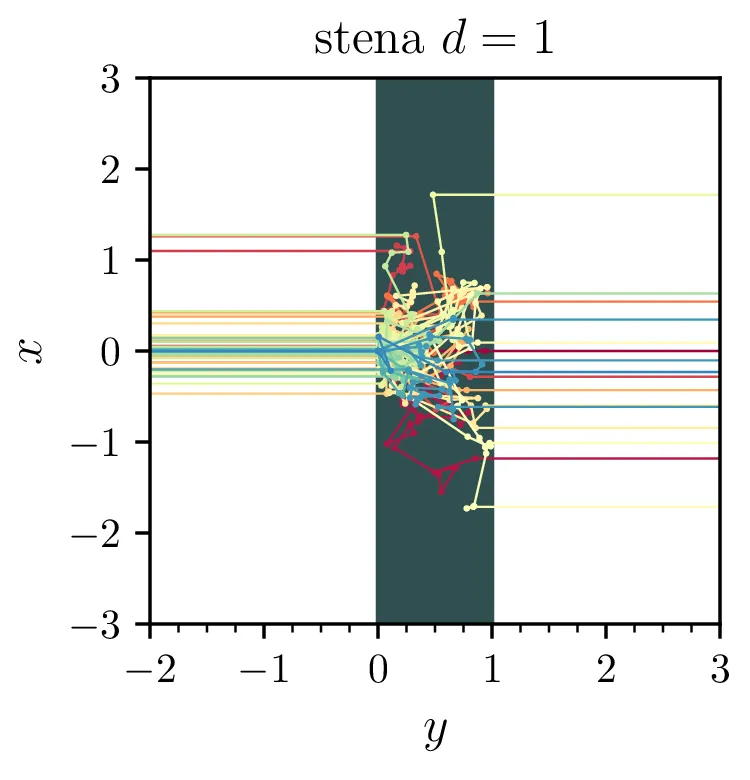
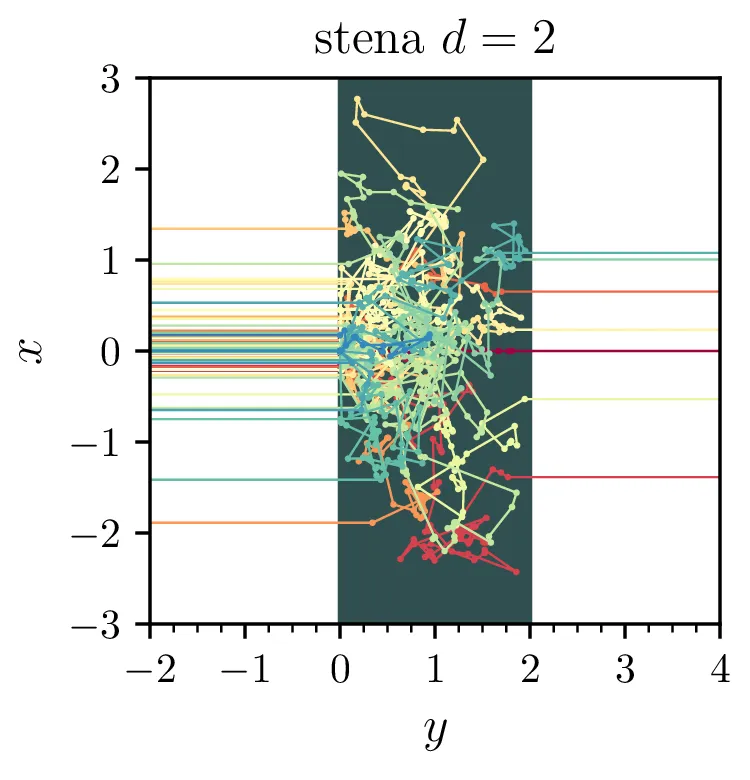
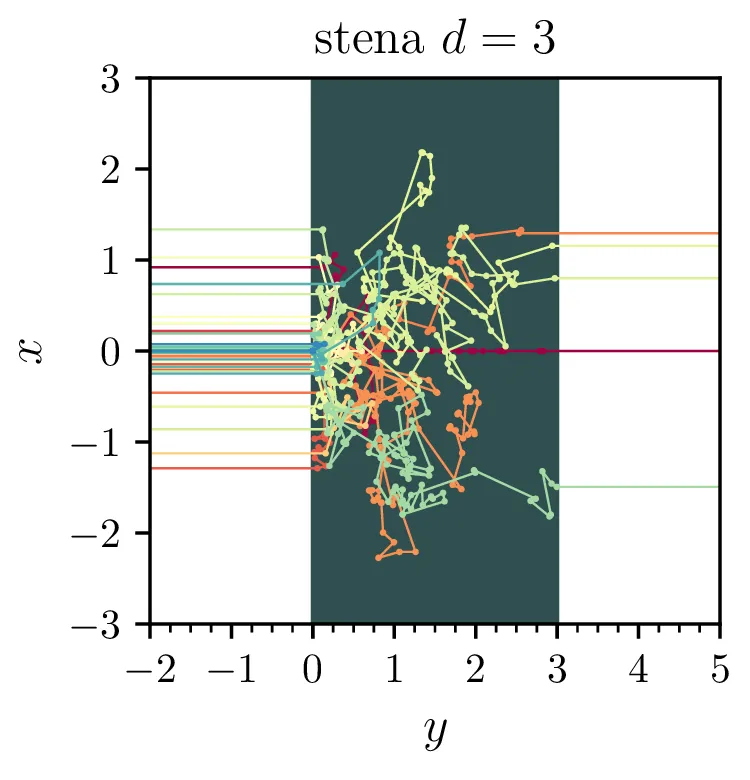
Obravnavamo nevtronski reflektor debeline \(d\), za katerega želimo računati verjetnost prepustnosti \(T\) in verjetnost odboja \(R\). Model je invarianten na sočasno skaliranje povprečne proste poti \(\langle \ell \rangle\) in debeline reflektorja. Zato bomo pri simulacijah nastavili \(d\) na 1 in prosto pot \(\langle \ell \rangle = \frac{1}{\lambda}\) dejansko razumeli kot razmerje proste poti in debeline reflektorja.

Model bomo z MC integracijo simulirali kot ansamble \(M\times N\) za naključne hode \(N\) delcev. Glede na dimenzijo, v kateri bomo problem reševali, bomo položaje nevtronov po vstopu v reflektor posodabljali sledeče

1-dimenzionalni model, kjer vsak korak naključno izberemo znak \(\mathcal{S} \in \{-1, 1\}\) in korak \(\ell \sim \lambda e^{-\lambda x}\), nato pa položaj korakamo kot \(x_{t + \Delta} = x_t + \ell \mathcal{S}\). Zagotovimo, da je prvi \(\mathcal{S}_0 = 1\).
2-dimenzionalni model, kjer vsak korak naključno izberemo kot \(\phi \in U(0, 2\pi)\) in korak \(\ell \sim \lambda e^{-\lambda x}\), nato pa položaj korakamo kot \(x_{t + \Delta} = x_t + \ell \cos(\phi)\), po potrebi pa še \(y_{t + \Delta} = y_t + \ell \sin(\phi)\).
3-dimenzionalni model, kjer vsak korak naključno izberemo kot \(\vartheta \in \arccos\big( U(-1, 1) \big)\) in korak \(\ell \sim \lambda e^{-\lambda x}\), nato pa položaj korakamo kot \(x_{t + \Delta} = x_t + \ell \cos(\vartheta)\), po potrebi pa še radij \(\rho_{t + \Delta} = \rho_t + \ell \sin(\vartheta)\).

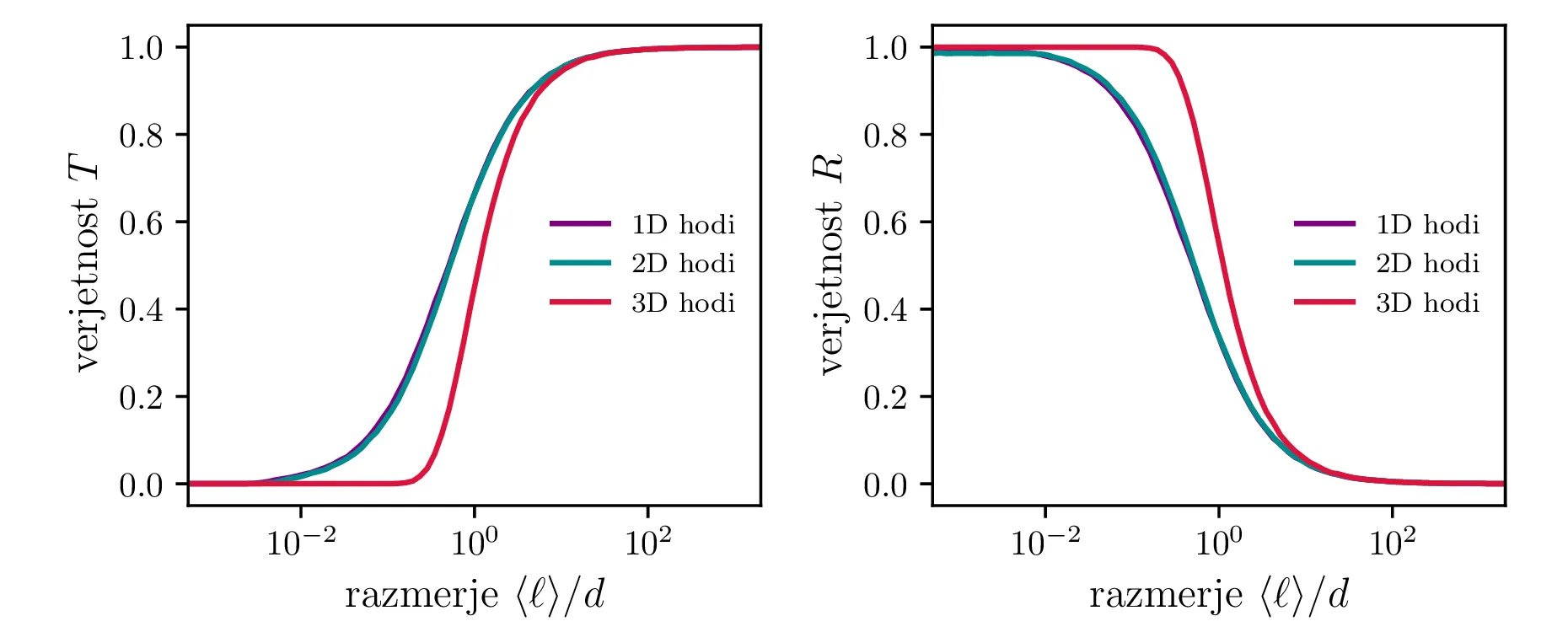
Primere posameznih realizacij za \(N = 100\) delcev v 2-dimenzijskem modelu vidimo na sliki 9. Že takoj vidimo, da je debelejši reflektor bolj odbojen. Modele v različnih številih dimenzij lahko neposredno primerjamo (slika 11) in opazimo, da se 1D in 2D izotropni model precej dobro ujemata, 3D izotropni model pa ima drugačno značilno obliko \(T\) in \(R\).

Časovna omejitev

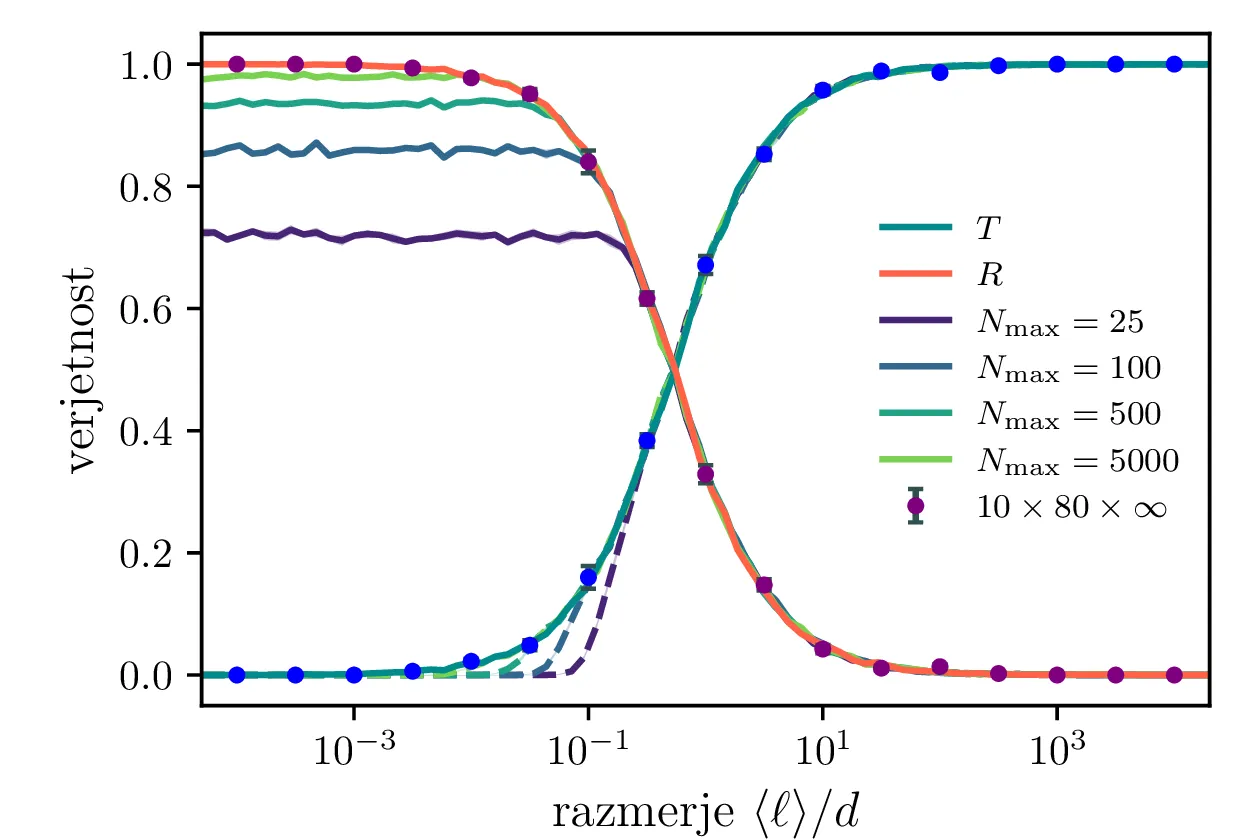
Prikaz prepustnosti \(T\) (modra črta) in odbojnosti \(R\) (oranžna črta) za \(M = 10\) ansambel po \(500\) delcev za 2-dimenzijski model (kot na sliki 9). Za manjši ansambel \(10\times 80 \times \infty\) so narisane posamezne točke z označeno napako. Za vse te krivulje je \(N_\mathrm{max} = \infty\), kar pomeni, da število korakov ni navzgor omejeno. Narisane so tudi \(T\) odvisnosti za ansamble \(10\times 500\times N_\mathrm{max}\) pri \(N_\mathrm{max} \in \{ 25, 100, 500, 5000 \}\), kjer lahko opazimo, da se prepustnost za zelo majhne \(\langle \ell \rangle / d\) ustali pri vrednosti manjši od \(1\). To je posledica mnogih nevtronov, ki v omejenem času preprosto ne zapustijo reflektorjevega volumna, ne v eno ne v drugo smer.

Na sliki 10 sta narisani \(T\) in \(R\) za 2-dimenzijski model. Razvidna je sigmoidna oblika, kjer je za majhne proste poti \(\langle \ell \rangle\) značilna visoka odbojnost \(R \sim 1\) in majhna prepustnost \(T \sim 0\), ravno obratno pa pri velikih \(\langle \ell \rangle\). Te pričakovane obliki sta nekoliko zmoteni, če pri korakanju uvedemo maksimalno število korakov \(N_\mathrm{max}\), kot nekakšno časovno omejitev. Tedaj je za majhne \(\langle \ell \rangle\) odbojnost \(R < 1\), hkrati pa je propustnost še vedno \(T \sim 0\). Tako imamo na videz nesmiselno situacijo \[T + R < 1,\] ki pa je pravzaprav posledica tega, da znotraj omejitve števila korakov nevtroni sploh ne zapustijo volumna reflektorja. To sicer ni primerno za simulacijo stacionarnega stanja, lahko pa bi postalo smiselno za modeliranje nekega časovno zamejenega procesa.

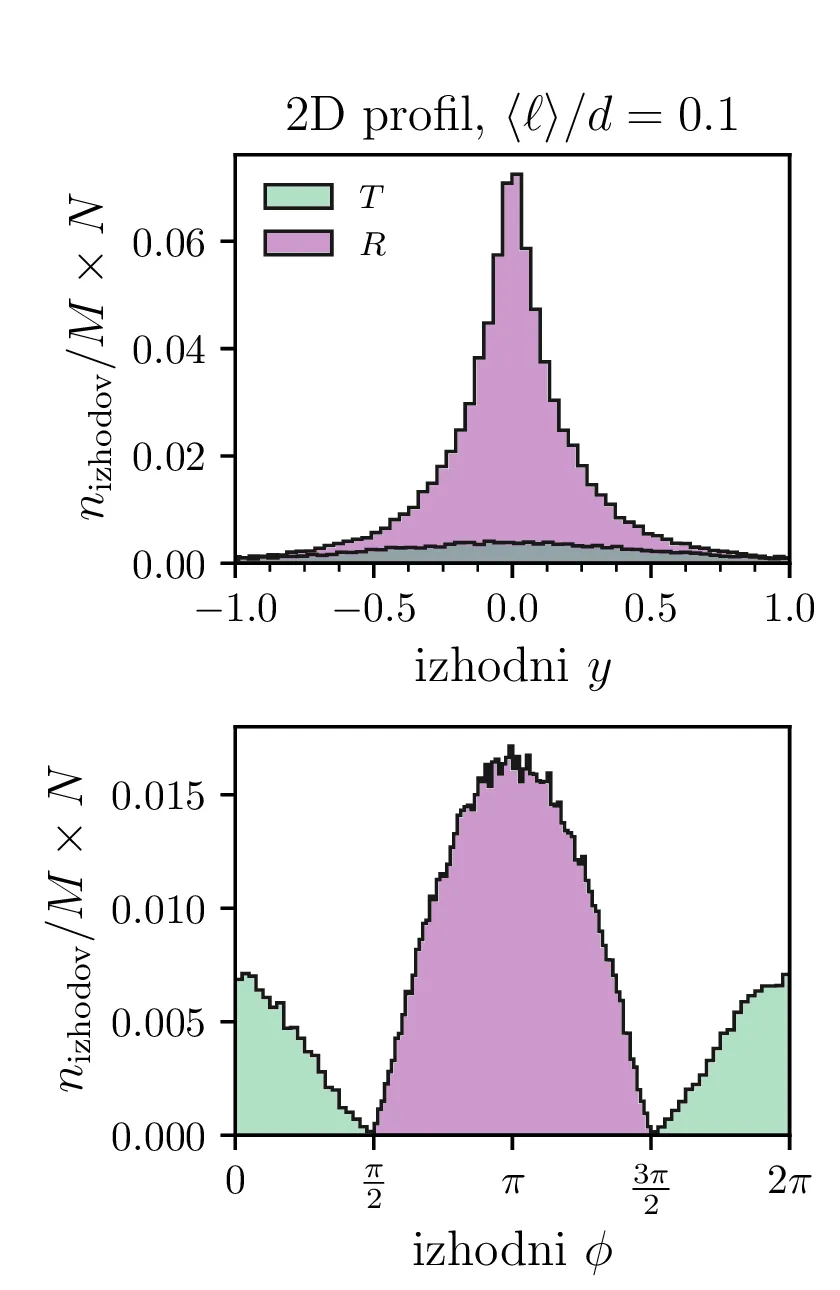
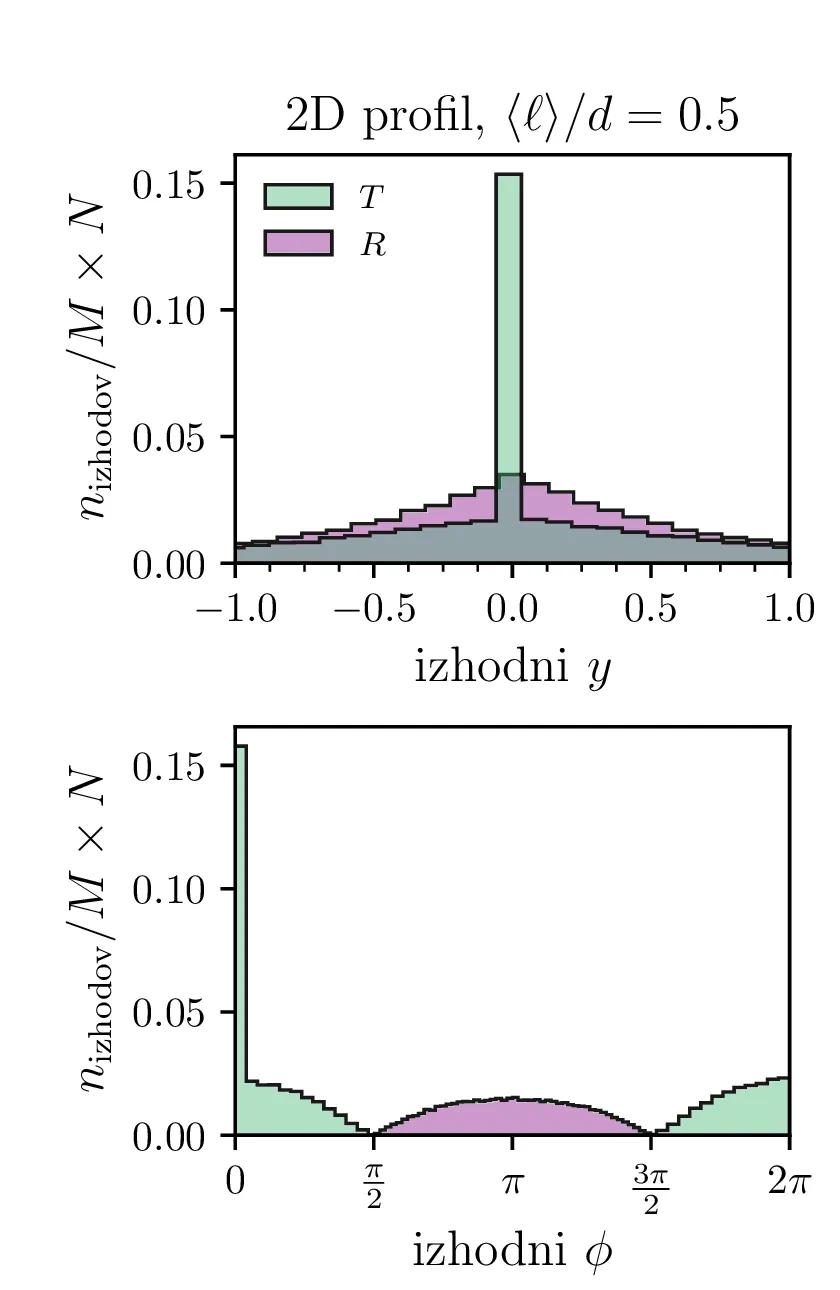
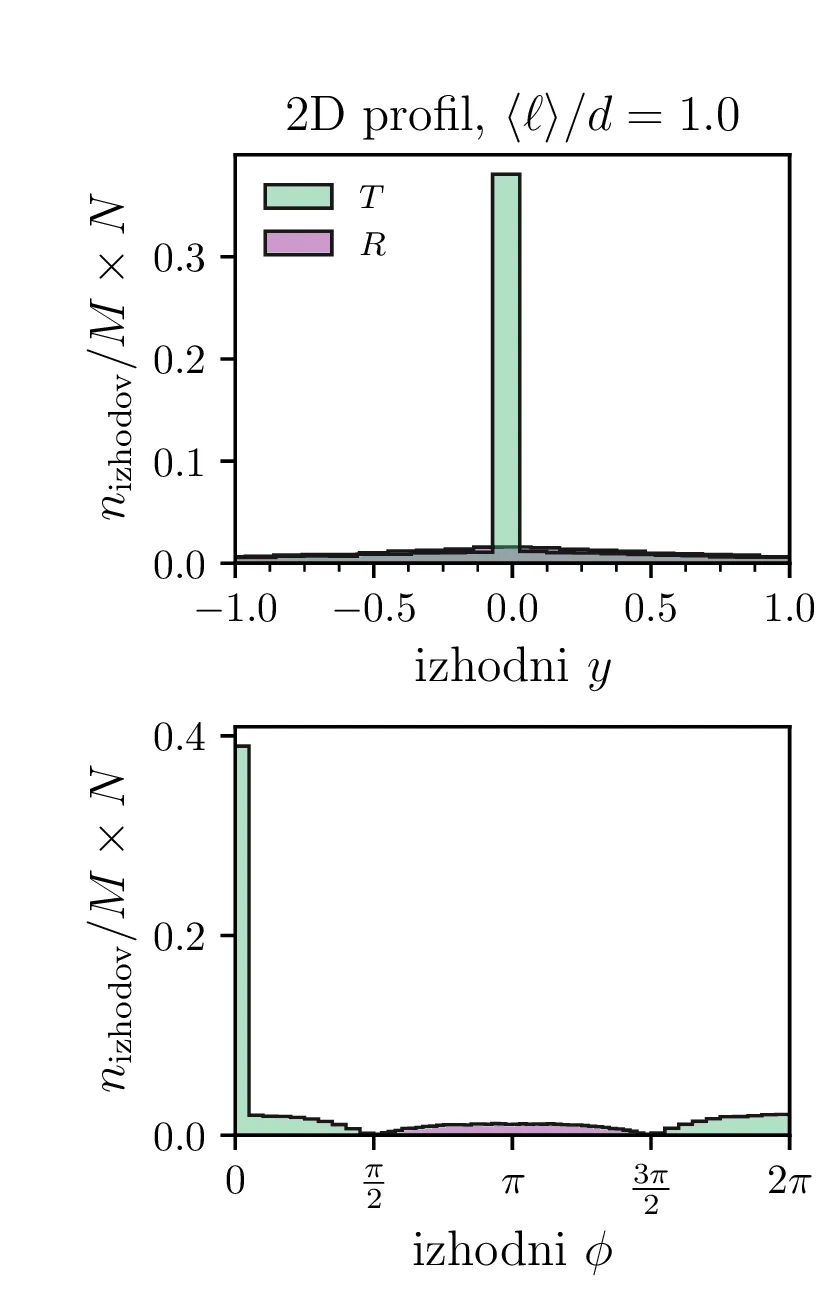
Primerjava izotropnih 1D, 2D in 3D modelov. Izračun z \(M = 10\) ansambli po \(5000\) trajektorij, brez omejitve maksimalnega števila korakov. Vidimo, da sta 1-dimenzijski in 2-dimenzijski izotropni model skoraj ekvivalentna. Znatno pa se razlikuje izotropni 3-dimenzijski model, ki ga karakterizira strmejši in kasnejši porastek prepustnosti \(T\), ko večamo povprečno prosto pot \(\langle \ell \rangle\) (ali manjšamo debelino reflektorja).

Profili prepuščenih in odbitih nevtronov

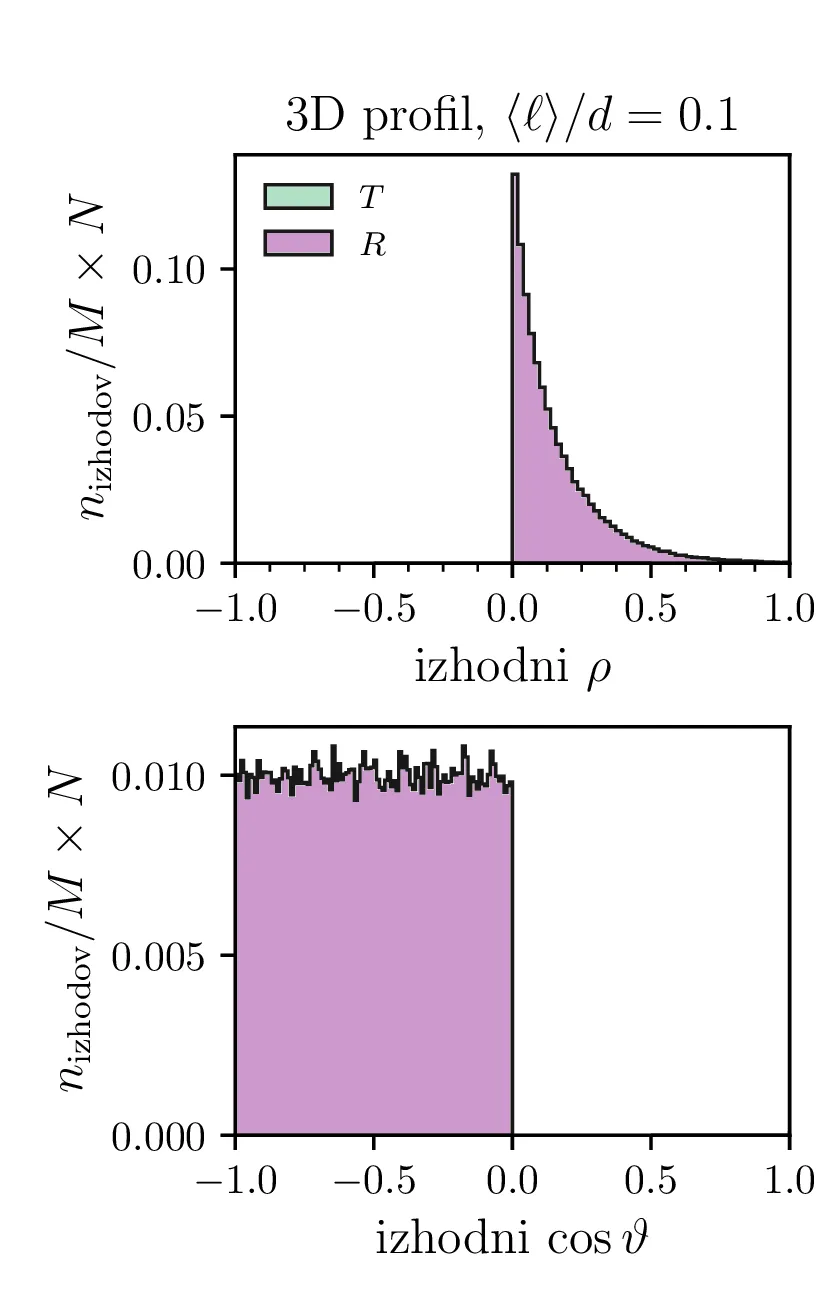
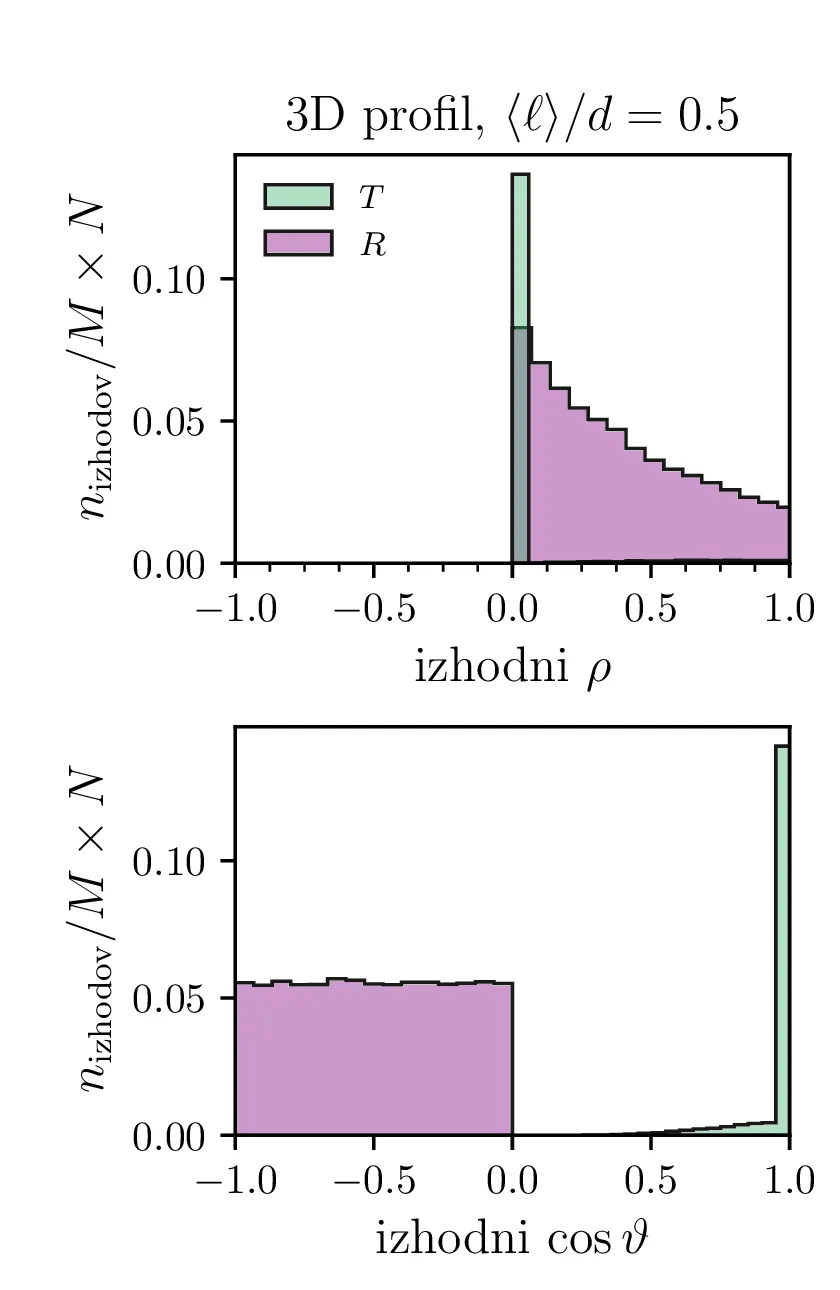
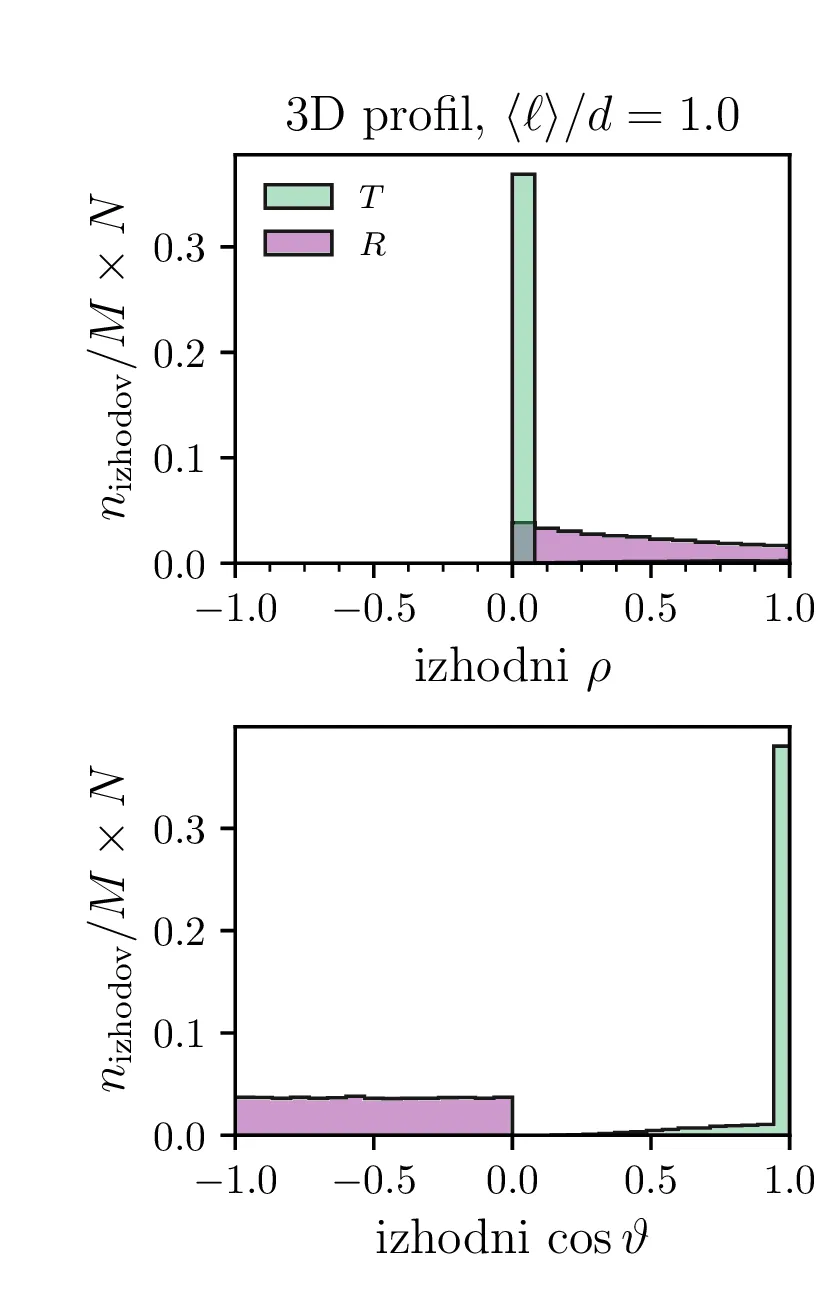
Pogledamo si lahko še nekaj porazdelitev nevtronov. Sicer nas bo za 2-dimenzijski model zanimala porazdelitev po koordinati \(y\) in po kotu \(\phi\), pod katerim potuje nevtron ko zapusti reflektor na levi (odbit nevtron) ali desni strani (prepuščen nevtron). Take profile za nekaj različnih razmerij \(\langle \ell \rangle\) vidimo na sliki 12. Tako kot v 2D modelu gledamo izhodna \(y\) in \(\phi\), gledamo v 3D modelu izhodno radialno cilindrično koordinato \(\rho\) in kot \(\cos\vartheta\). Profile po \(\rho\) in \(\cos\vartheta\) narišemo na sliki 13.

Na podlagi teh profilov lahko 2D in 3D model primerjamo. Za oba modela npr. velja, da tanek reflektor z visoko prepustnostjo \(T\) prepusti zelo usmerjen curek (glej 12 in 13). A modela se razlikujeta po tem, kako učinkovit je tanjši reflektor (v 3D modelu je že precej tanjši reflektor zelo dober in ima \(R \sim 1\)). Za 3D model pa je značilno še to, da odbiti nevtroni po odboju iz reflektorja izhajajo izotropno (glej slike 13 spodaj).

Histogramirani profili izhodnih prepuščenih in odbitih nevtronov po koordinati \(y\) in po izhodnemu kotu \(\phi\) za 2-dimenzijski model in različne \(\langle \ell \rangle\). Normalizirano na število vseh nevtronov v ansamblu \(M\times N\). Po špicah za \(\langle \ell \rangle = 0.5\) in \(1.0\) vidimo, da so prepuščeni nevtroni za tanek reflektor zelo usmerjeni, za tanek reflektor pa se znatno bolj porazdelijo (leva slika).

Histogramirani profili izhodnih prepuščenih in odbitih nevtronov po cilindrični radialni koordinati \(\rho\) in po izhodnemu kotu \(\cos\vartheta\) za 2-dimenzijski model in različne \(\langle \ell \rangle\). Normalizirano na število vseh nevtronov v ansamblu \(M\times N\). Podobno kot v 2D modelu (sika 12) je prepuščeni curek skozi tanko ploščo visoko usmerjen. Hkrati pa v 3D modelu že tanjši reflektor \(\langle \ell \rangle = 0.1\) praktično ne prepušča nevtronov (leva slika). Zanimiva je tudi konstantna porazdelitev odbitih nevtronov po \(\cos\vartheta\), ki ustreza izotropni porazdelitvi tega kota sferičnih koordinat – odbiti nevtroni torej znotraj reflektorja povsem izgubijo informacijo o svoji začetni smeri in iz njega na levi strani izhajajo izotropno.

Viri

[1]

J. H. Hubbard in B. H. West, Differential Equations: A Dynamical Systems Approach: Ordinary Differential Equations. New York: Springer, 1991.

[2]

S. P. N. Ernst Hairer Gerhard Wanner, Solving Ordinary Differential Equations: Nonstiff Problems, 2. izd., let. 2. v Springer Series in Computational Mathematics 8, vol. 2. Springer-Verlag Berlin Heidelberg, 1993.

Modelska analiza I 7. naloga: Naključna števila in integracije z metodo Monte Carlo