Modelska analiza I
6. naloga: Luščenje modelskih parametrov
Navodila
-
V farmakologiji merijo odziv tkiv na različne reagente. Za večino teh pojavov lahko privzamemo, da gre za reakcijo, kjer spremljamo vezavo molekul reagenta X na receptorje Y v tkivu. \[Y + X \rightleftharpoons Y^*.\] V stacionarnem stanju dobimo zvezo \begin{equation}y = \frac{y_0 x}{x + a}. \label{eq:pharm}\end{equation} Iz merskih podatkov v datoteki
farmakoloski.datdoloči parametra \(y_0\) in \(a\), kjer pomeni \(y_0\) nasičeni odziv tkiva in \(a\) koncentracijo, potrebno za odziv, ki je enak polovici nasičenega. Napaka v meritvi odziva je v vsem področju enaka trem enotam. Zvezo lahko lineariziramo. Pazi, kako se pri tem transformirajo napake. Določi še parametre razširjenega nelinearnega modela \begin{equation}y = \frac{y_0 x^p}{x^p + a^p}, \label{eq:pharm-nonlinear}\end{equation} in zagovarjaj statistično upravičenost vpeljave dodatnega parametra \(p\). -
Poišči najboljšo vrednost za čistilnost ledvic iz kliničnih podatkov v datoteki
ledvice.datz uporabo enorazdelčnega in dvorazdelčnega modela ter primerjaj rezultate. Pri dvorazdelčnem modelu lahko za začetni približek vzameš eksponentni konstanti v razmerju \(1:10\). Ali je dodatek aditivne konstante (“ozadje” pri štetju razpadov) statistično upravičen? Poskusiš lahko tudi s funkcijo \(e^{-\lambda\sqrt{t}}\), ki jo izvedemo iz bolj zapletenih modelov. Spremenljivka \(t\) v podatkih je čas na sredi vsakega merilnega intervala. -
Za uporabo visokoločljivostnega magnetnega spektrometra potrebujemo preslikavo, ki iz izmerjenih količin rekonstruira parametre trajektorije delcev, potrebne za izračun energije in drugih kinematičnih količin. V datoteki
thtg-xfp-thfp.datnajdete kalibracijske podatke z meritvami \(\vartheta_\mathrm{tg}\) (disperzijski kot na tarči v stopinjah) za različne \(x_\mathrm{fp}\) (položaj v goriščni ravnini v milimetrih) in \(\vartheta_\mathrm{fp}\) (kot v goriščni ravnini v stopinjah). Natančnosti meritev kotov so velikostnega reda miliradianov, položajev pa okrog milimetra. Sestavi varčni model za preslikavo \[(x_\mathrm{fp}, \vartheta_\mathrm{fp}) \mapsto \vartheta_\mathrm{tg}.\] Uporabiš lahko na primer najnižje potence \(x_\mathrm{fp}\) in \(\vartheta_\mathrm{fp}\) ali pa kakšne druge funkcije teh dveh spremenljivk. Za izbiro relevantnih členov lahko uporabiš SVD razcep in reduciran \(\chi^2\).
Farmakološki odziv
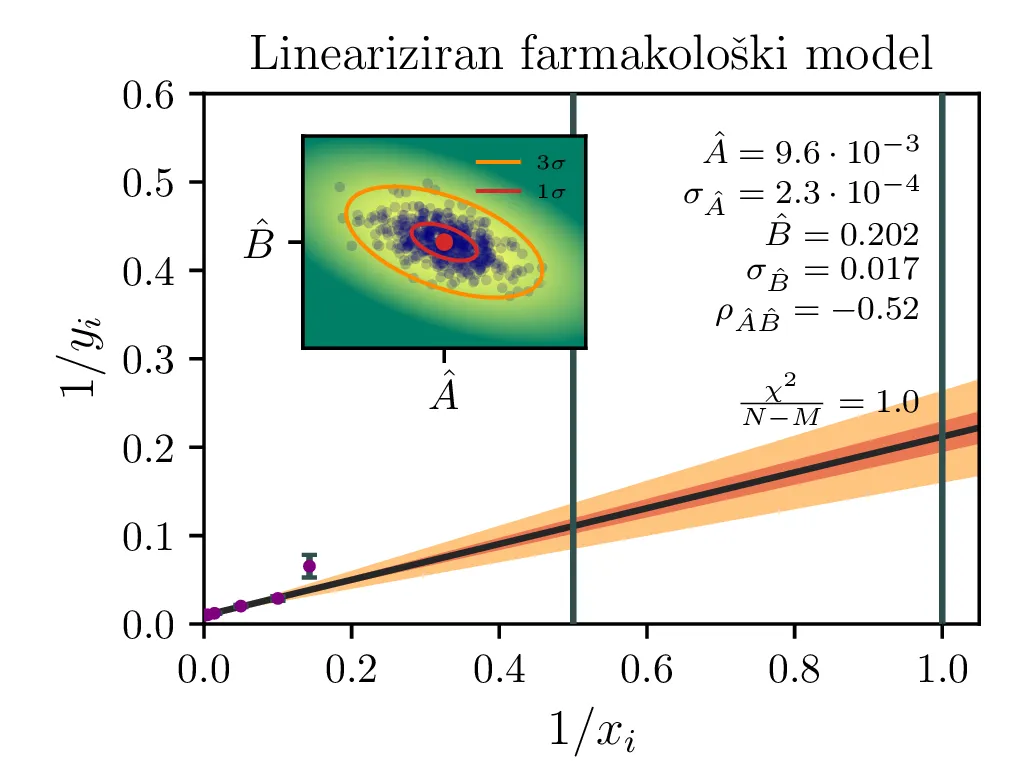
Model s funkcijsko obliko (1) lahko reduciramo na navadno (sicer obteženo, saj napake izmerkov zdaj niso več enake) linearno regresijo z modelom oblike \begin{equation}\frac{1}{y} = A + B \left( \frac{1}{x} \right), \label{eq:pharm_lin}\end{equation} pri čemer sta parametra novega modela \begin{equation}A \vcentcolon=\frac{1}{y_0}, \quad B = \frac{a}{y_0}. \label{eq:ya-to-AB}\end{equation}
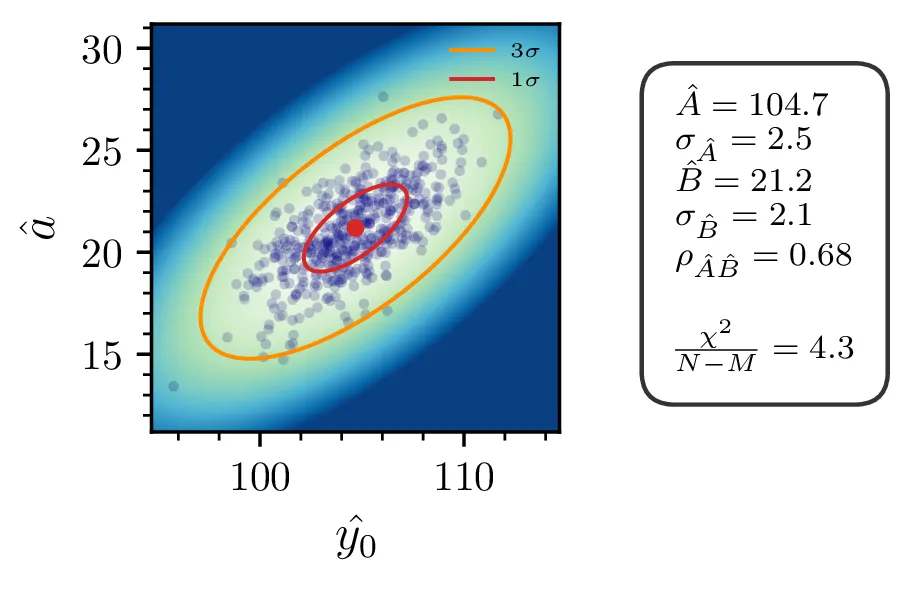
Izmerki \(y_i\) za model imajo napako \(\sigma_y = 3\), a z uvedbo novih spremenljivk se napaka spremeni kot \(\sigma_{\frac{1}{y}} = \frac{\sigma_y}{y^2}\) in postano mnogo večja za majhne \(y\). Z obteženo metodo najmanjših kvadratov, kjer minimiziramo \[\chi_\beta^2 \vcentcolon=\sum_i \frac{(y_i - \hat{y}_\beta(x_i))^2}{\sigma_i^2},\] pri čemer je \(\hat{y}\) naša predpostavljena modelska funkcija, parametrizirana z vektorjem \(M\) parametrov \(\mathbf{\beta}^T = \begin{bmatrix} \beta_1, \dots, \beta_M \end{bmatrix}\), v našem primeru \[\hat{y}_\beta(x) = A + B x, \quad \beta = \begin{bmatrix} A \\ B \end{bmatrix}.\] Optimizacijska metoda, ki jo bomo uporabili, nam bo vrnila kovariančno matriko za vektor parametrov \[\Omega_\beta \vcentcolon=\begin{bmatrix} \sigma_A^2 & \sigma_{AB} \\ \sigma_{AB} & \sigma_B^2 \end{bmatrix}\] Ko prehajamo med različnimi parametri \([A, B]\) in \([y_0, a]\), moramo upoštevati kako se transformirajo napake. Za to je najbolj priročno zapisati kar Jakobian transformacije med enimi in drugimi parametri \begin{equation}J = \begin{bmatrix} \nabla^T y_0(A, B) \\ \nabla^T a(A, B) \end{bmatrix} = \begin{bmatrix} \frac{-1}{A^2} & 0 \\ \frac{-B}{A^2} & \frac{1}{A} \end{bmatrix} \label{eq:jac}\end{equation} Tedaj lahko kovariantno matriko parametrov \(y_0, a\) v lineariziranem približku zapišemo s transformacijo \[\Omega_{[y_0, a]} \vcentcolon=\begin{bmatrix} \sigma_{y_0}^2 & \sigma_{y_0,a} \\ \sigma_{a,y_0} & \sigma_a^2 \end{bmatrix} \approx J \cdot \Omega_{[A, B]} \cdot J^T.\]
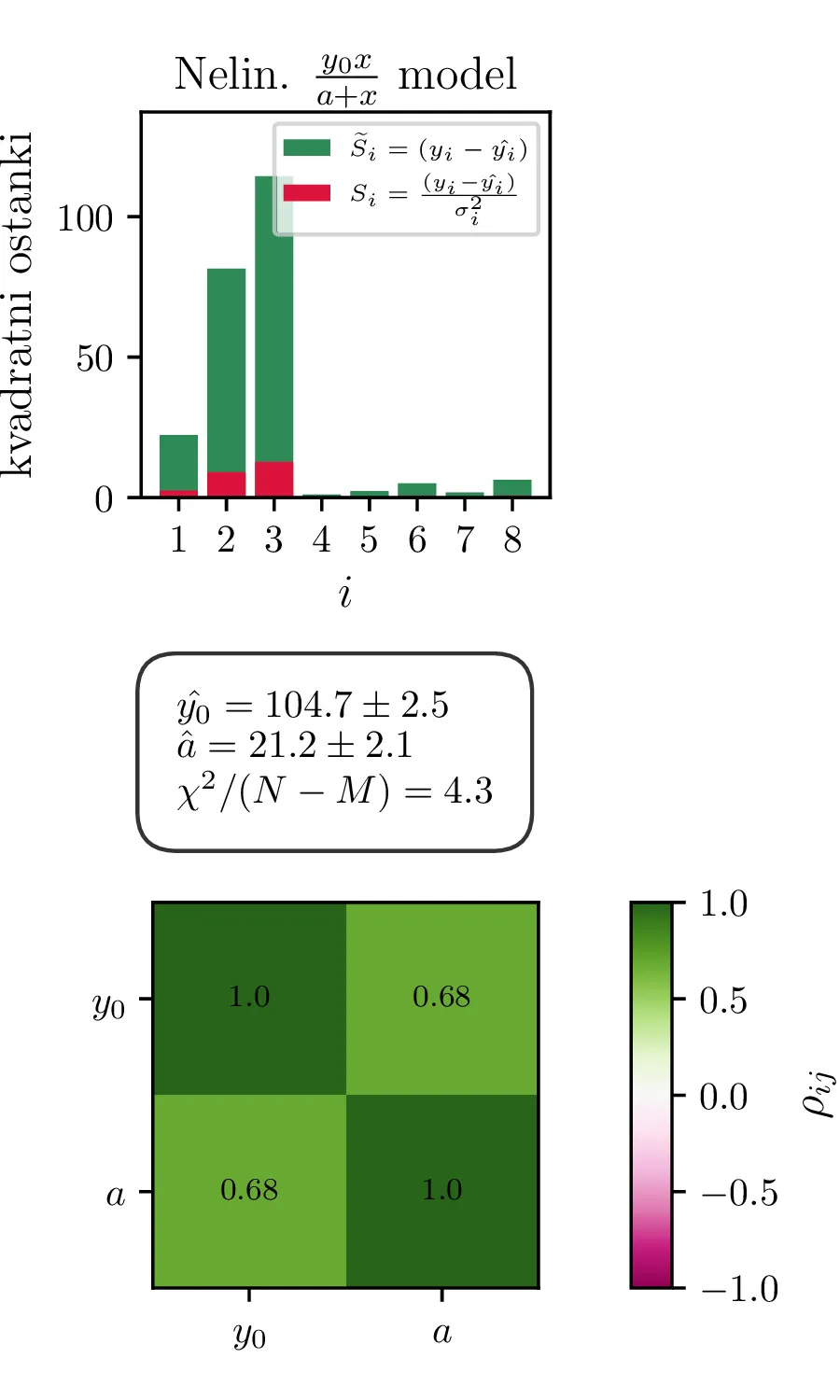
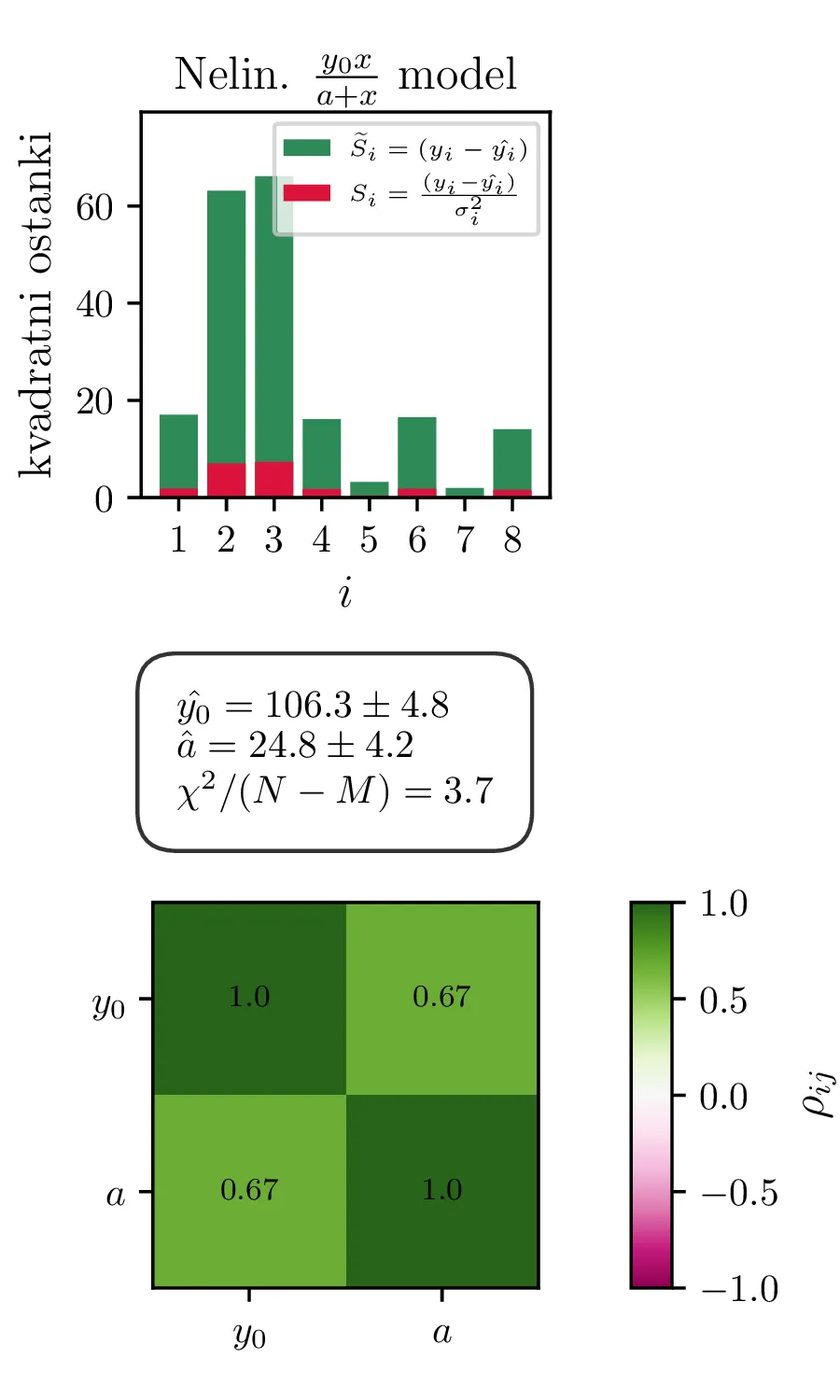
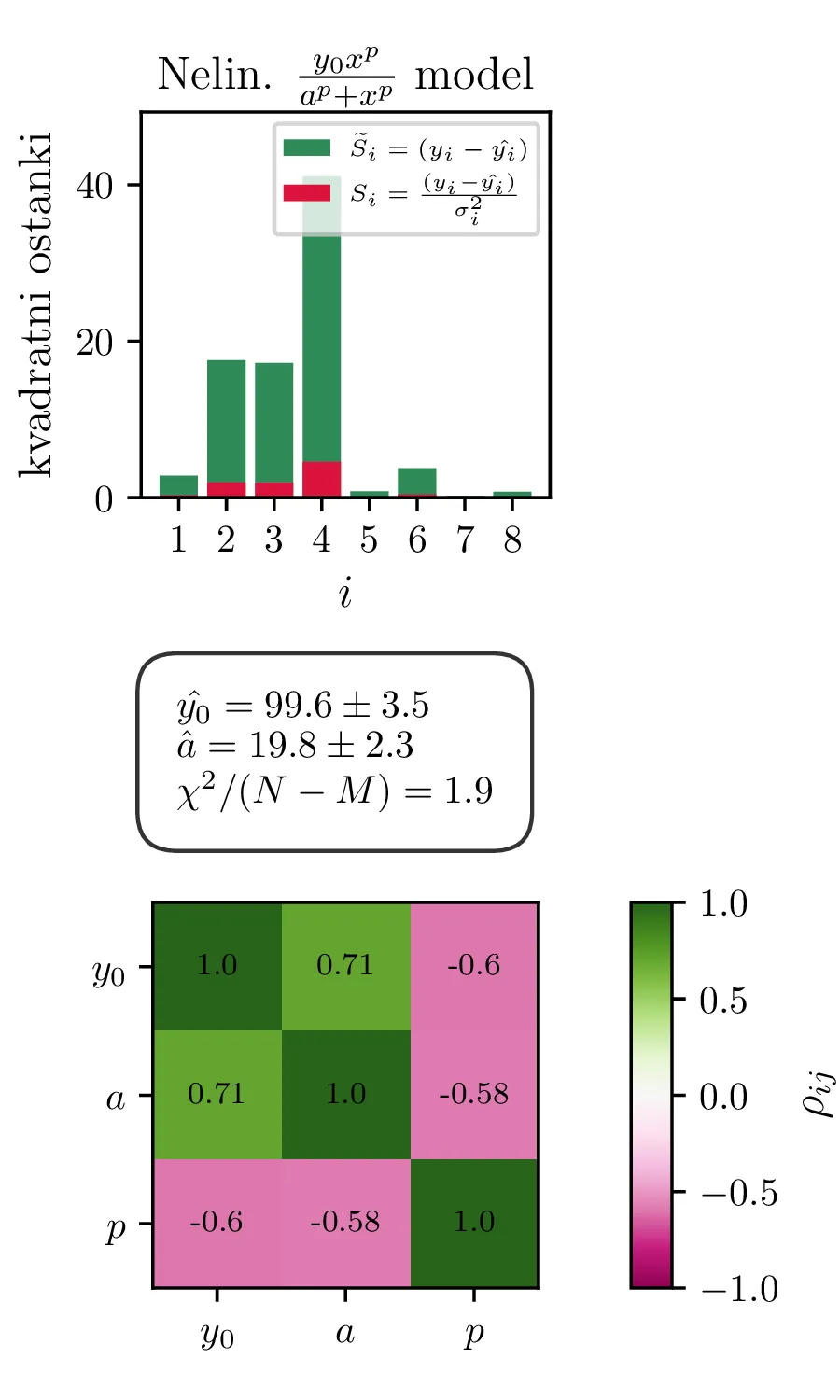
Primerjava modelov
Na podatkih farmakoloski.dat zdaj preizkusimo tri različne modele:
-
Lineariziran model \(1/y = A + B (1/x)\), parametra \(y_0, a\) nato dobimo z inverzno preslikavo (4), z Jakobianom (5),
-
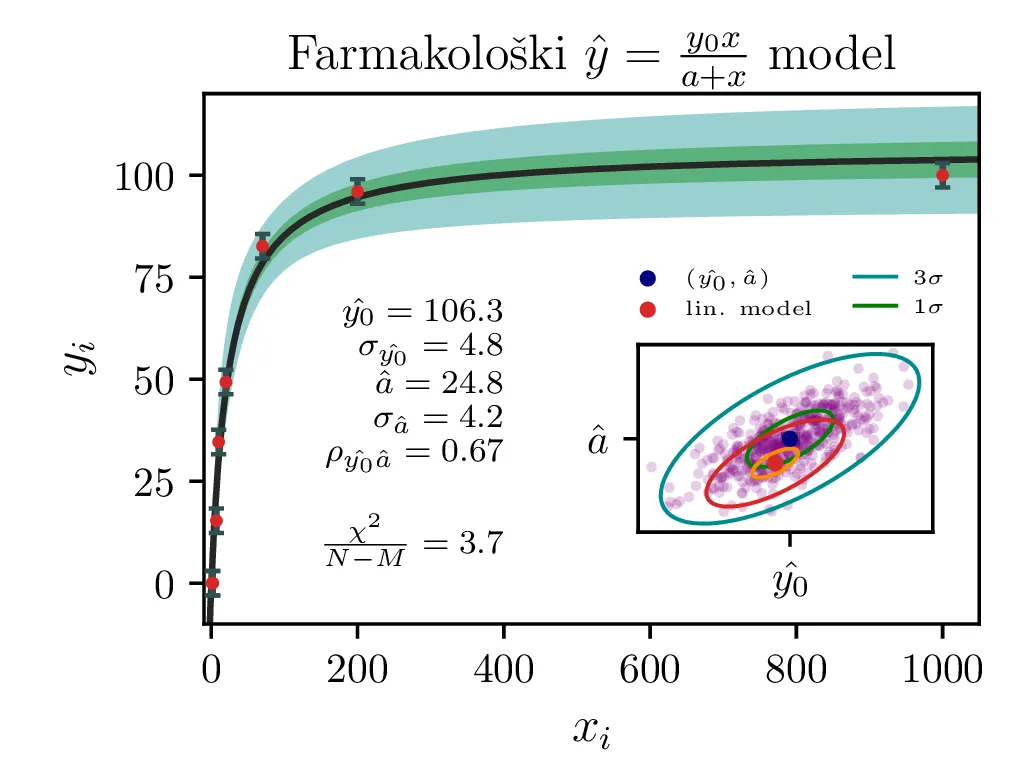
Model \(y = \frac{y_0 x}{x + a}\). Ta model je nelinearen v parametrih,
-
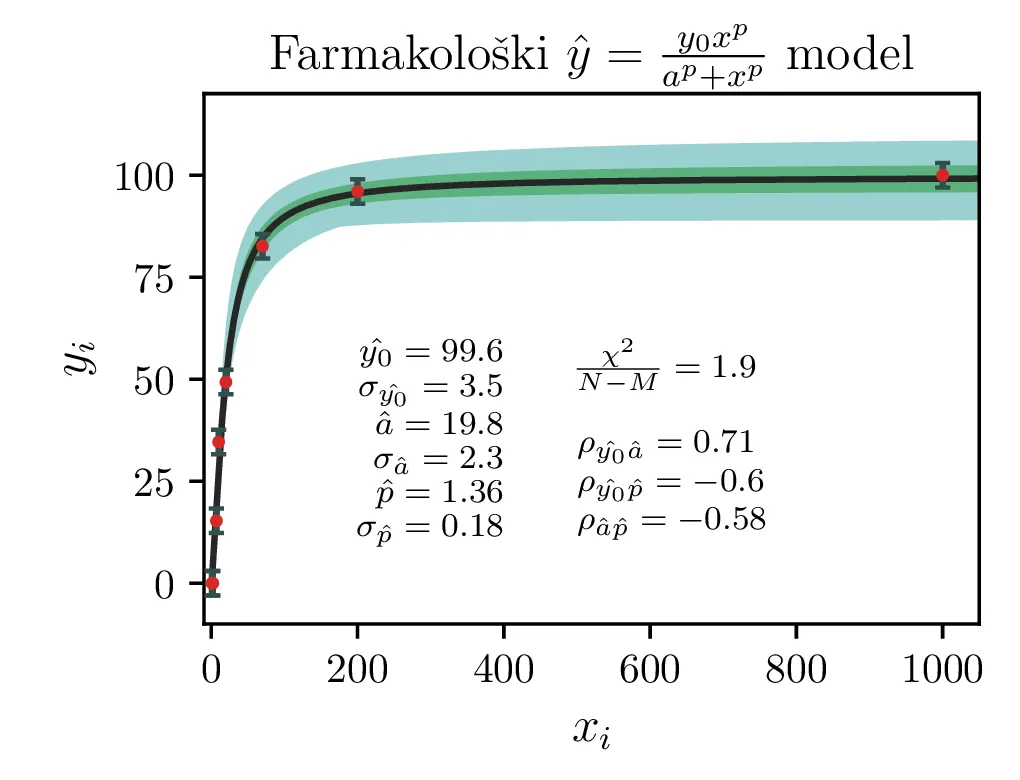
Izboljšan model \(y = \frac{y_0 x^p}{x^p + a^p}\) z dodatnim parametrom \(p\). Tudi ta model je nelinearen v parametrih.
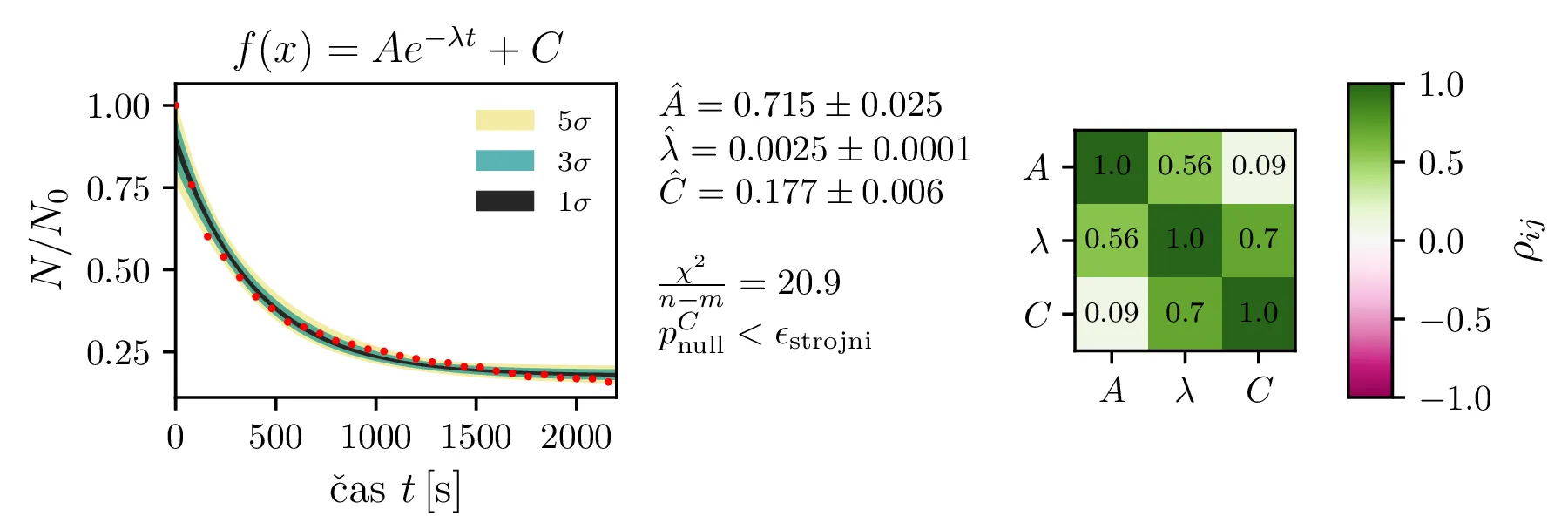
Rezultati in intervali zaupanja za 1. linearizirani model so prikazani na sliki 1 levo. Po transformaciji \((A, B) \mapsto (y_0, a)\) dobimo rezultat na sliki 1 desno. Po tej transformaciji dobimo za reducirani \(\chi^2\) vrednost \(4.3\), kar pomeni, da je model preveč preprost ali pa da so podcenjene naše napake. Nekoliko boljši \(\chi^2 / (N-1)\) nam da 2. model, nelinearizirani model funkcijske oblike (1).
Ker sta za 1. in 2. model reducirana \(\chi^2\) mnogo večja od \(1\), lahko upravičimo dodatni parameter \(p\) za model v obliki (2). Fit takšnega modela vidimo na sliki 2 desno. Dodatni parameter \(p\) nam model znatno izboljša, saj se reducirani \(\chi^2\) praktično razpolovi, njegova vrednost je \(1.9\).
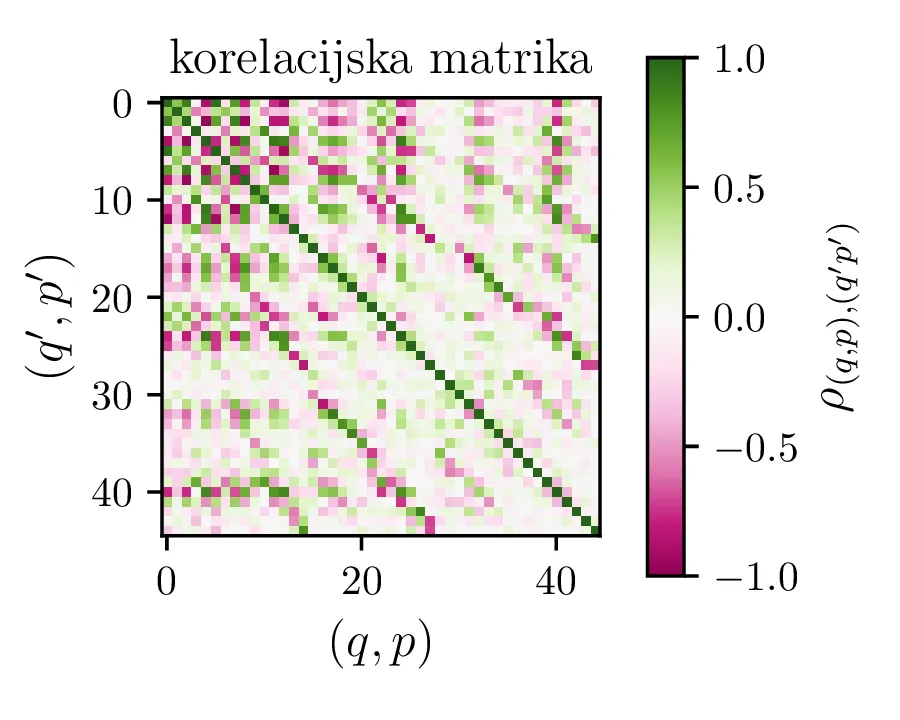
Vsi modeli kažejo določeno mero odvisnosti med dobljenimi parametri \(y_0, a, p\). To kvantificiramo z matriko Pearsonovih korelacij \[\rho_{ij} = \frac{\sigma_{ij}}{\sigma_i \sigma_j},\] pri čemer je \(\sigma_{ij}\) kovarianca dveh spremenljivk. Takšne korelacije so narisane na sliki 3 spodaj, kjer lahko vidimo, da so parametri za vse modele precej močno korelirani.
Razdelčni modeli ledvic
Na podatkih iz ledvice.dat bomo preizkusili modele sledečih funkcijskih oblik
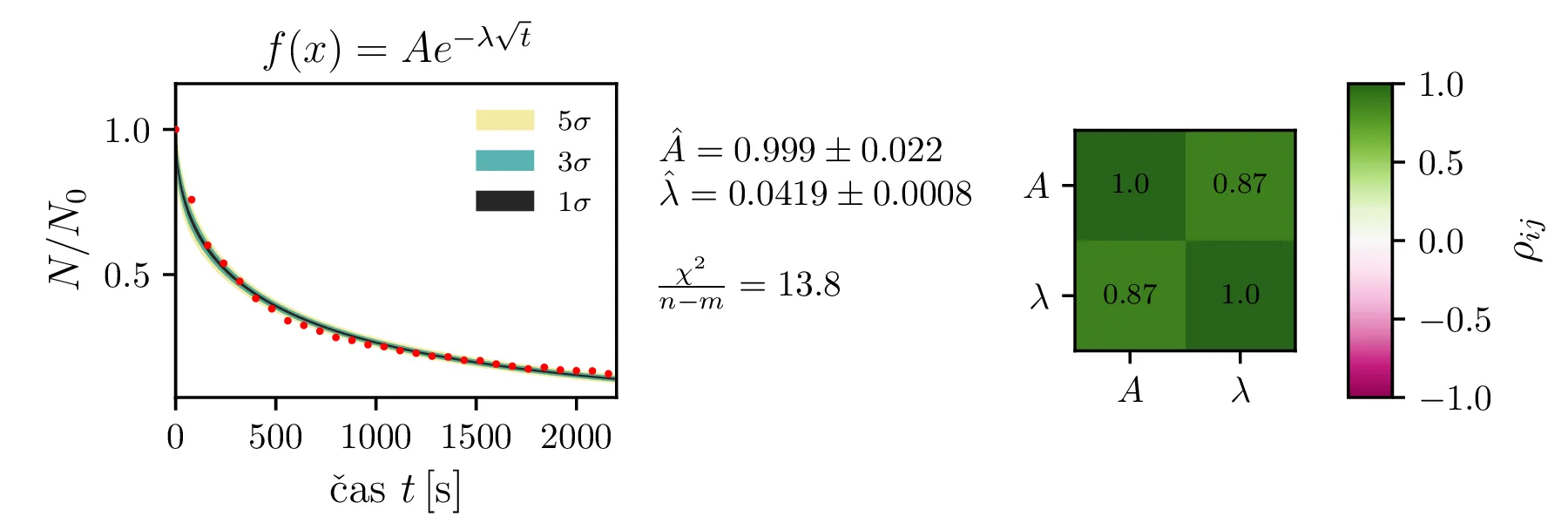
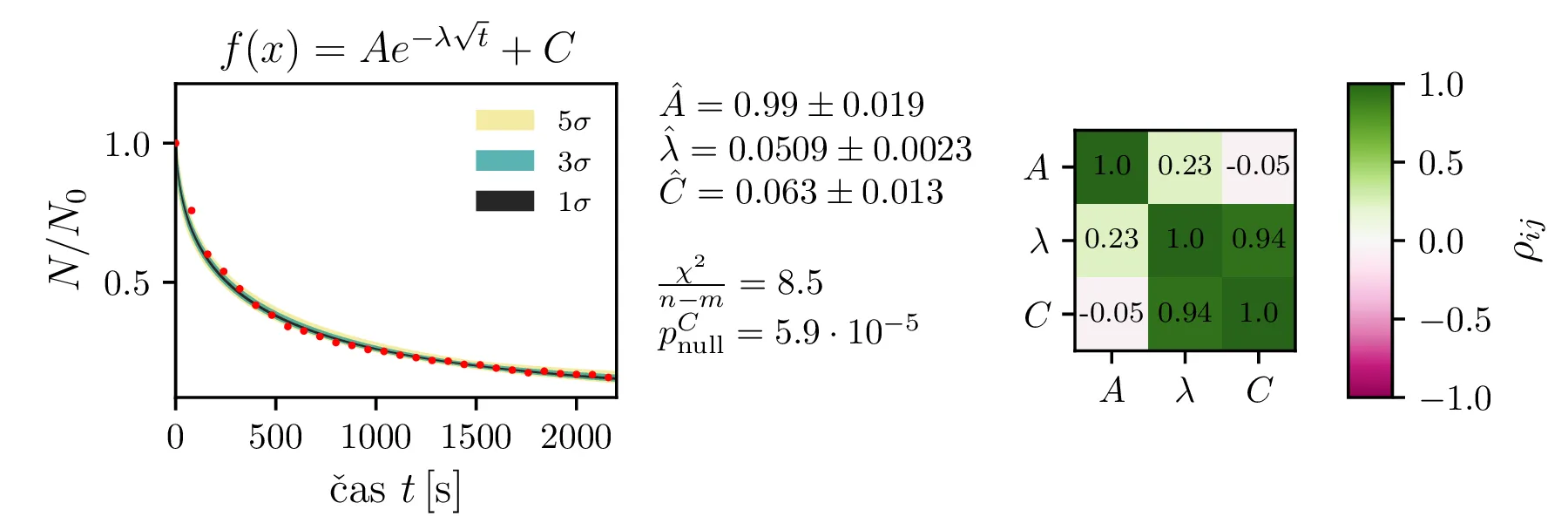
\begin{equation}\begin{aligned} &f_1(x) = A e^{-\lambda t} \label{eq:exp1} , \\ &f_2(x) = A e^{-\lambda t} +
C \label{eq:exp2} , \\ &f_3(x) = A e^{-\lambda \sqrt{t}} \label{eq:sqrt_exp1} , \\ &f_4(x) = A e^{-\lambda
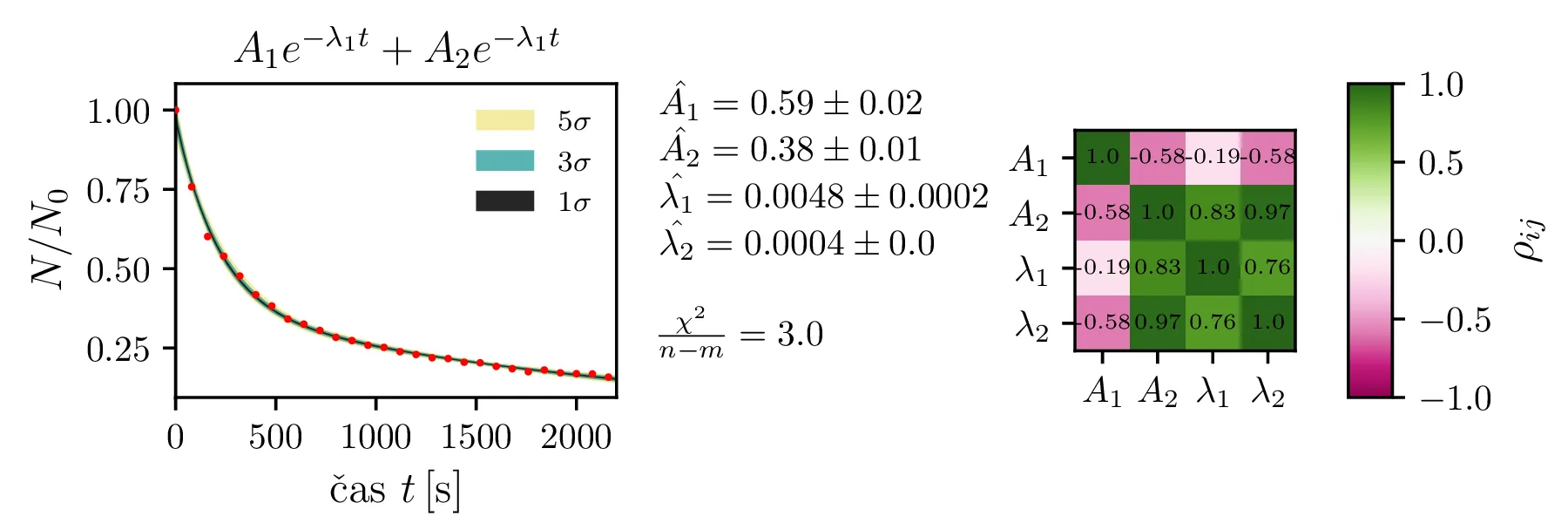
\sqrt{t}} + C \label{eq:sqrt_exp2} , \\ &f_5(x) = A_1 e^{-\lambda_1 t} + A_2 e^{-\lambda_1 t}
\label{eq:exp_double1} , \\ &f_6(x) = A_1 e^{-\lambda_1 t} + A_2 e^{-\lambda_1 t} + C \label{eq:exp_double2} ,
\\ &f_7(x) = A_1 e^{-\lambda_1 \sqrt{t}} + A_2 e^{-\lambda_1 t} \label{eq:sqrt_exp_double1} , \\ &f_8(x) = A_1
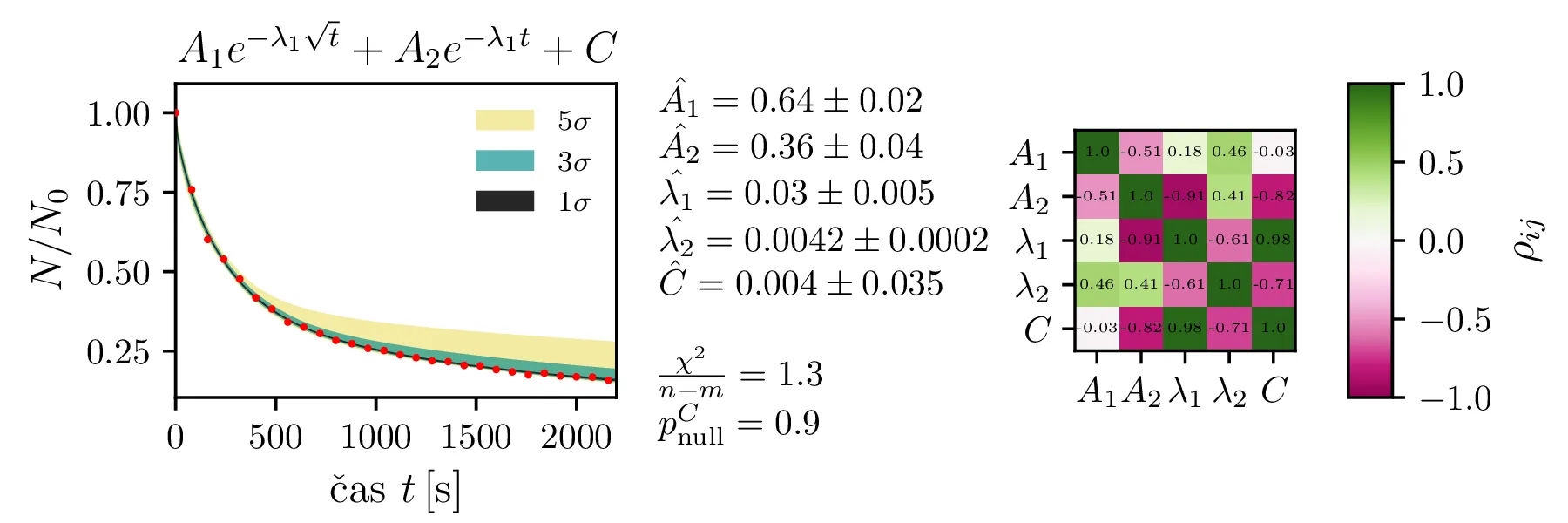
e^{-\lambda_1 \sqrt{t}} + A_2 e^{-\lambda_1 t} + C \label{eq:sqrt_exp_double2}.
\end{aligned}\end{equation}
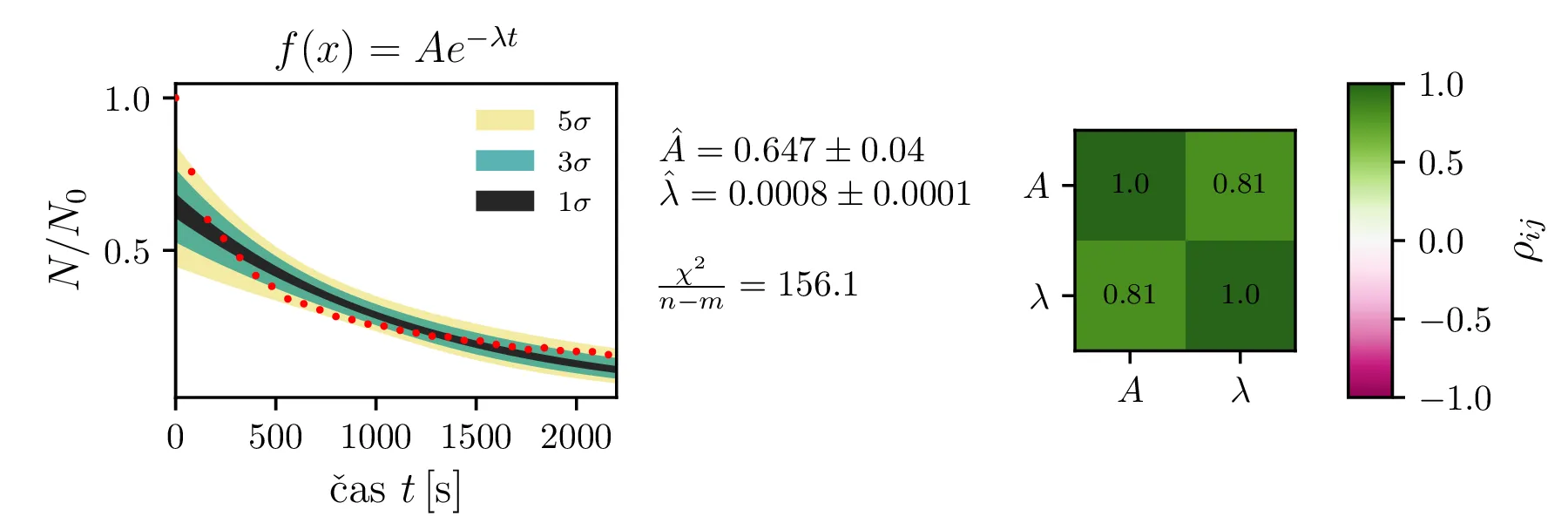
Rezultate modelov, njihove parametre in reduciran \(\chi^2\) predstavimo na
slikah 4, 6
in 7. Po dobljenem reduciranem
\(\chi^2\) se nedvoumno najbolje odreže model z enim korensko eksponentnim
členom in enim eksponentnim členom brez ozadja (oblika ([eq:sqrt_exp_double1])).
Napaka izmerkov
Ker je za podatki, ki jih merimo, proces radioaktivnega razpada, so naše naključne spremenljivke \(N(t_i)\) porazdeljene Poissonovsko. Tedaj je torej povsem naravno, da je tudi njihova varianca enaka \(N\), za napaka pa vzamemo \[\sigma_N \approx \sqrt{N}.\]
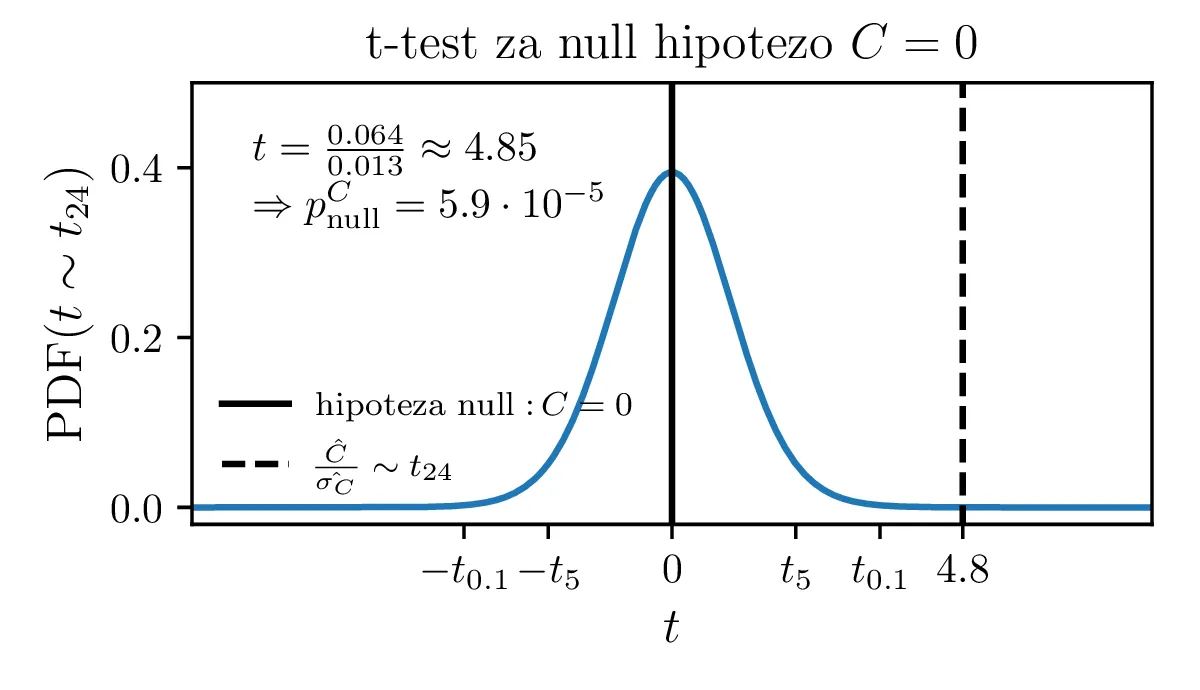
Upravičenost konstante ozadja
Predpostavimo lahko, da bi model izboljšali, če dodamo neko konstanto \(C\), ki predstavlja konstantno ozadje. Zanima nas, ali je dodatek takšne konstante upravičen. To bomo preverili z testom za statistiko \[t = \frac{\hat{C}}{\hat{\sigma_C}}.\] Vzorčno določena ocena parametra \(\hat{C}\) porazdeljena Gaussovsko, vzorčna ocena \(\hat{\sigma_C}\) pa po \(\chi^2_{N - M - 1}\) porazdelitvi, pri čemer je \(N\) število vzorcev, \(M\) pa število parametrov v funkcijski obliki za fit. Tedaj vemo, da je statistika porazdeljena po Studentovi t-porazdelitvi \[t \sim t_{N - M - 1},\] Zdaj nas zanima verjetnost nulte hipoteze \[\text{null: } C = 0,\] ki jo določimo kot verjetnost obojestranskih repov t-porazdelitve. Na sliki 5 je prikazan primer za model \(Ae^{-\lambda\sqrt{t}} + C\), kjer je število prostostnih stopenj 24. Ker lahko nulto hipotezo ovržemo z p-vrednostjo \(6.1 \cdot 10^{-5}\), lahko rečemo, da je dodatek konstante ozadja statistično upravičen.
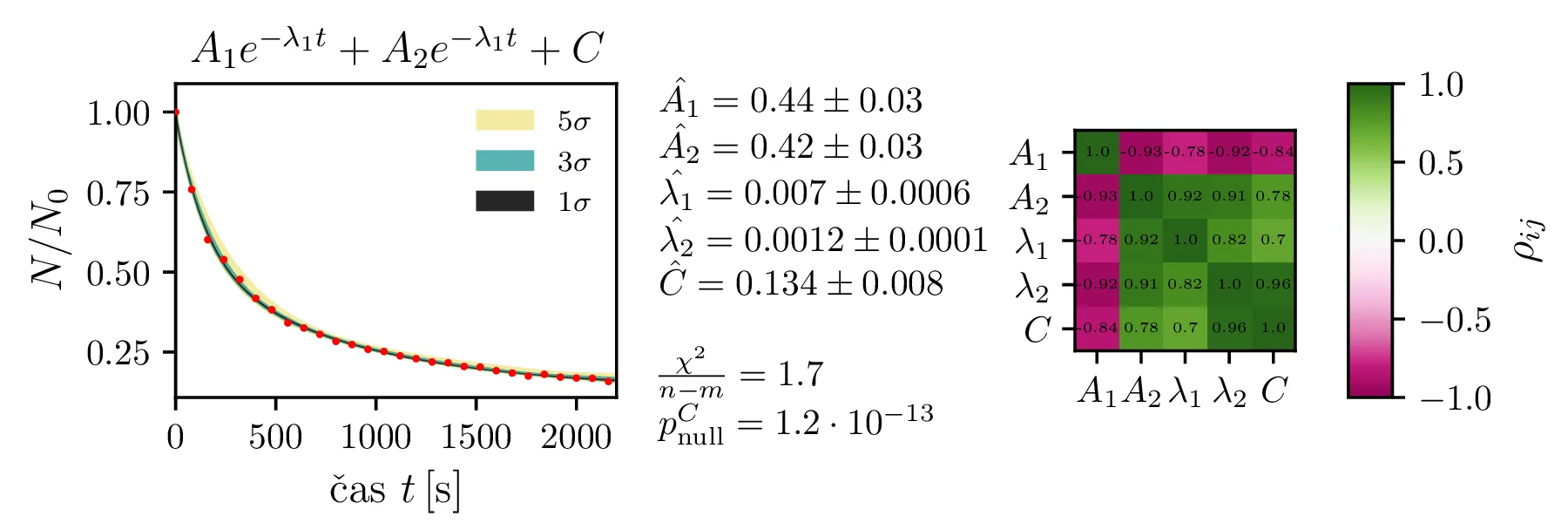
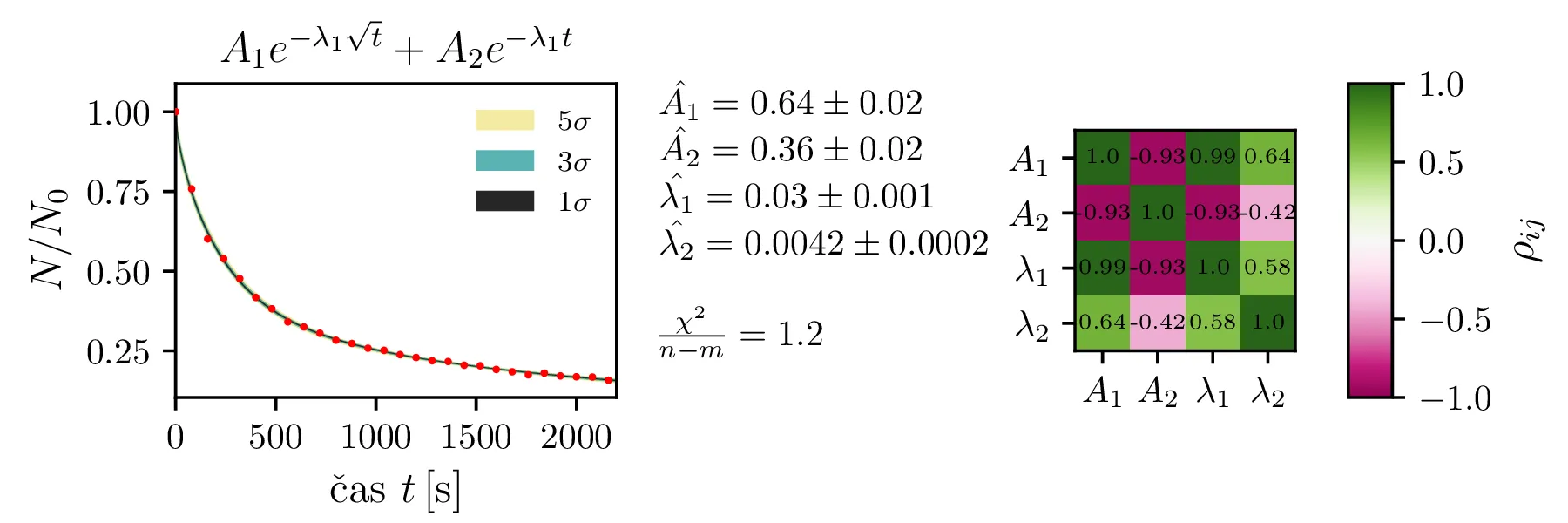
Magnetni spektrometer
Meritve imamo podane v koordinatah \(\vartheta_\mathrm{fp}, x_\mathrm{fp}\) in narisane na sliki 8 levo. Na podlagi nekega visoko-dimenzijskega fita bomo izbrali za napako v izmerjenih kotih \(\vartheta_\mathrm{tg}\) vrednost \[\sigma_{\vartheta_\mathrm{tg}} = 5.5 \,\mathrm{mrad}.\] V namen numerične stabilnosti in lažje izbire baznih funkcij jih najprej pretvorimo v nove koordinate, določene z linearno transformacijo \begin{equation}\begin{bmatrix} X \\ Y \end{bmatrix} = \begin{bmatrix} 0.00787 & 0 \\ -0.00974 & 0.00840 \end{bmatrix} \begin{bmatrix} \vartheta_\mathrm{fp}\\ x_\mathrm{fp} \end{bmatrix} - \begin{bmatrix} 0.0345 \\ -0.155 \end{bmatrix}. \label{eq:skew}\end{equation} Meritve v novih koordinatah vidimo na sliki 8 desno, kjer padejo v normaliziran \([-1, 1]\times[-1, 1]\) kvadrat.
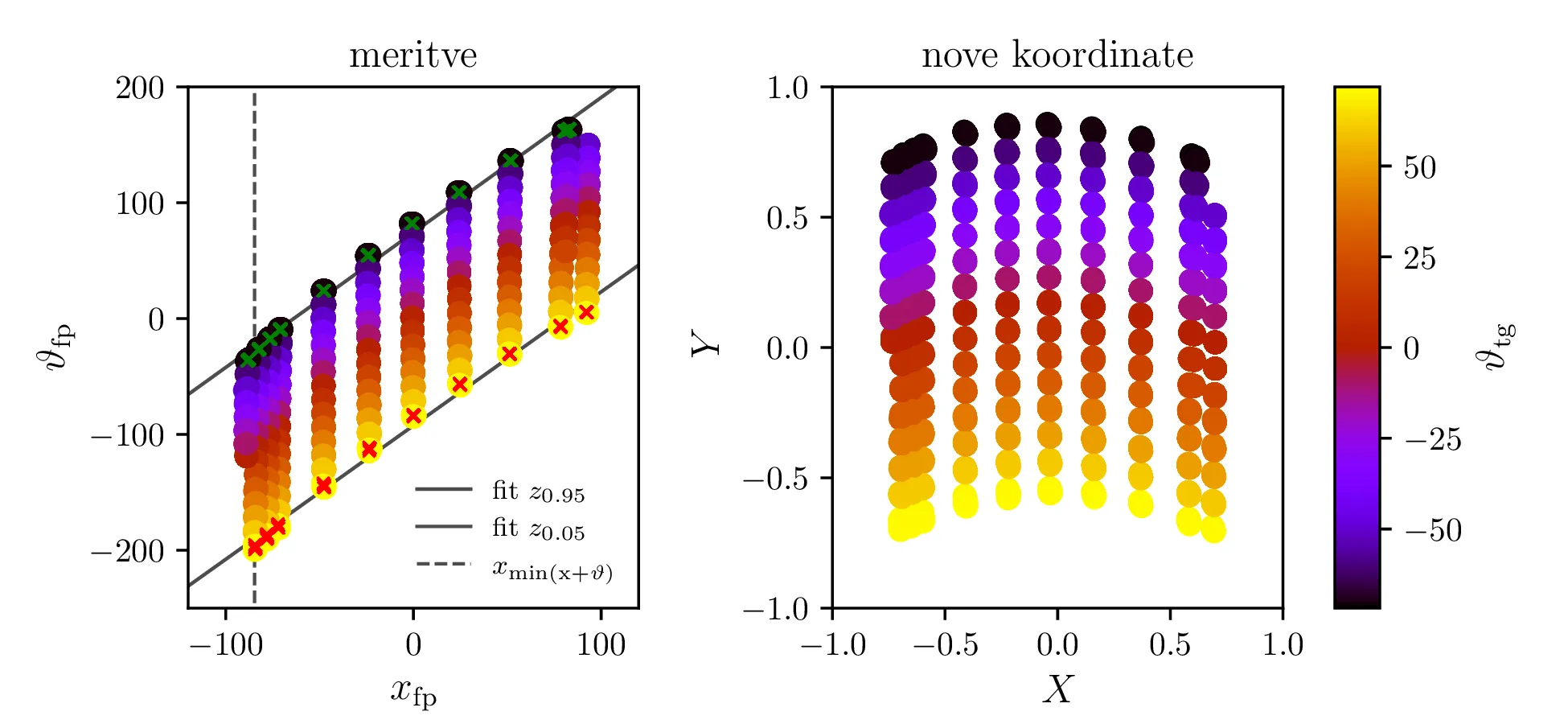
Bazne funkcije
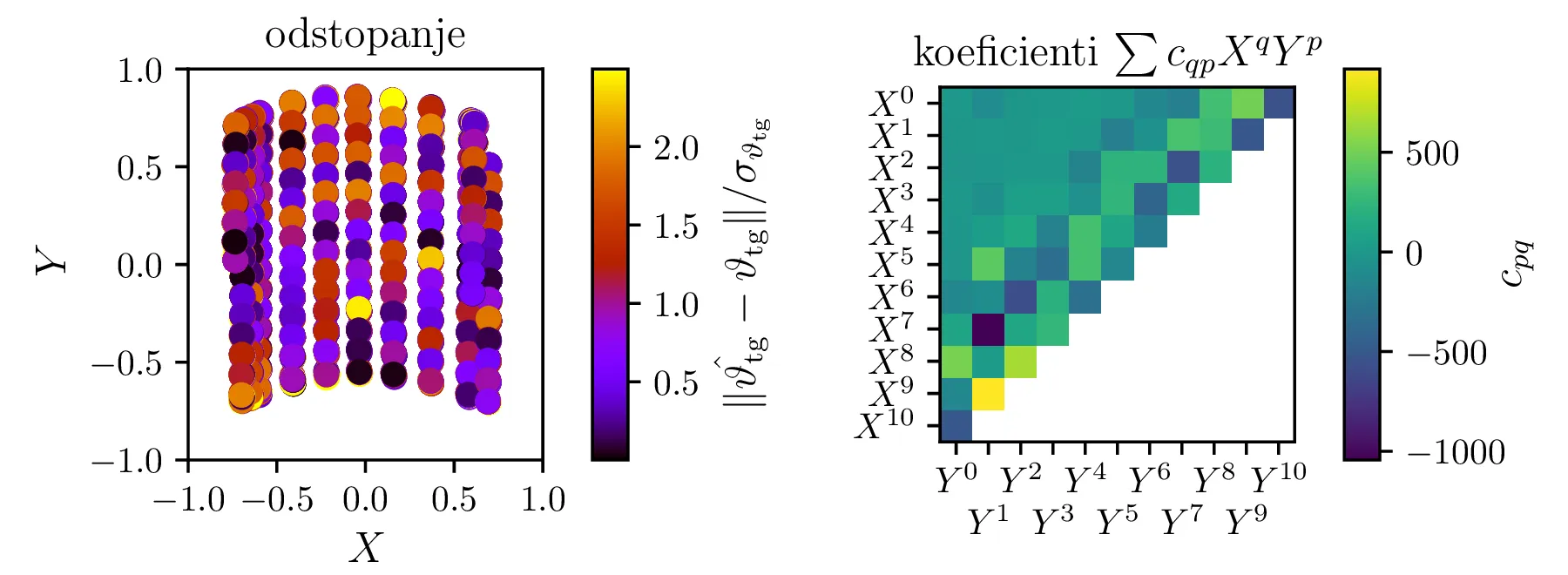
Za modelsko funkcijo bomo vzeli v koordinatah \(X, Y\) polinome v dveh spremenljivkah \[\hat{\vartheta_\mathrm{tg}}^{(K)}(X, Y) = \sum_{q + q \le K} c_{qp} X^q Y^p.\] Za linearno regresijo s takšnimi baznimi funkcijami bomo formirali matriko \(A\) z indeksi stolpcev \((p, q) = 1, 2, \dots, M\), pri čemer je število vseh parametrov v modelu enako \[M = \frac{(K+1)(K+2)}{2},\] vrstice matrike \(A\) za izmerke \(i = 1, 2, \dots, N\) pa so oblike \[A_{i, \bullet} = \begin{bmatrix} 1 & X_i & Y_i & X_i^2 & X_i Y_i & Y_i^2 & \dots \end{bmatrix}.\] Na sliki 9 vidimo odstopanja od meritev in koeficiente samih členov za \(K = 10\). Reduciran \(\chi^2\) takega modela z \(M = 45\) prostimi koeficienti \(c_{qp}\) je \[\chi^2 / (N - M) = 1.34.\] V nadaljevanju bomo modele izboljšali predvsem tako, da bomo začeli z večjim številom prostih parametrov \(M\), nato pa bomo parameter odstranjevali do točke, ko to ne bo bistveno pokvarilo modela.
Chebyebishevi polinomi kot alternativna baza
Kot alternativo polinomski \(X^q Y^p\) bazi sem poskusil model tudi z produktno
bazo Chebyebishevi polinomov, torej kot
\[\hat{\vartheta_\mathrm{tg}}^{(K)}(X, Y) = \sum_{q + q \le K} c_{qp} T_q(X) T_p(Y),\]
pri čemer sta \(T_q\) in \(T_p\) Chebyebisheva
polinoma redov \(q\) in \(p\), izvrednotena
kar z SciPy metodo scipy.special.chebyt. Ob uporabi te nove baze se prilagajanje obnaša nekoliko
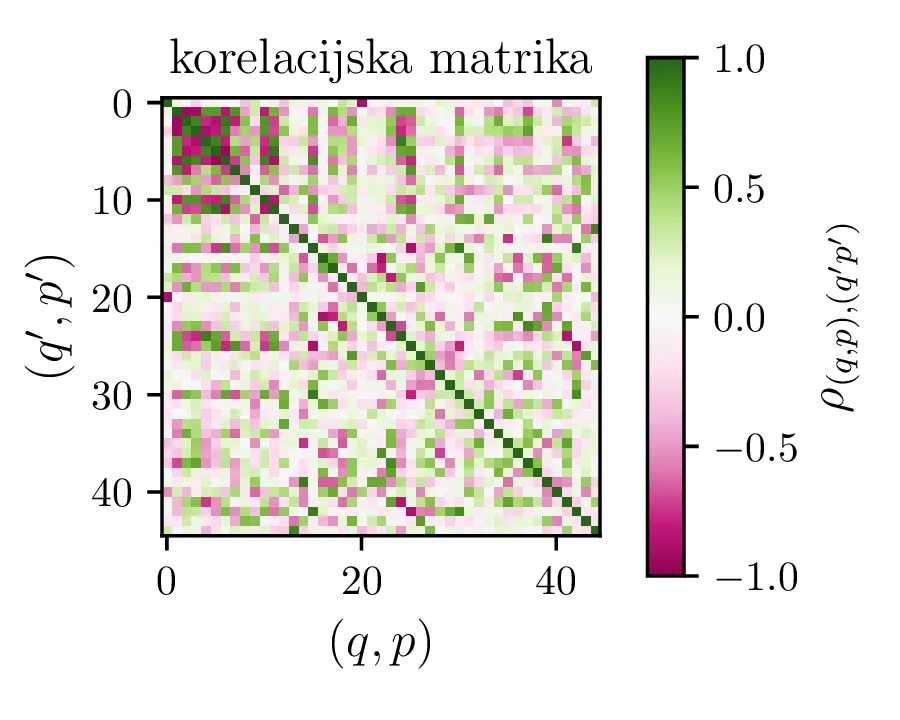
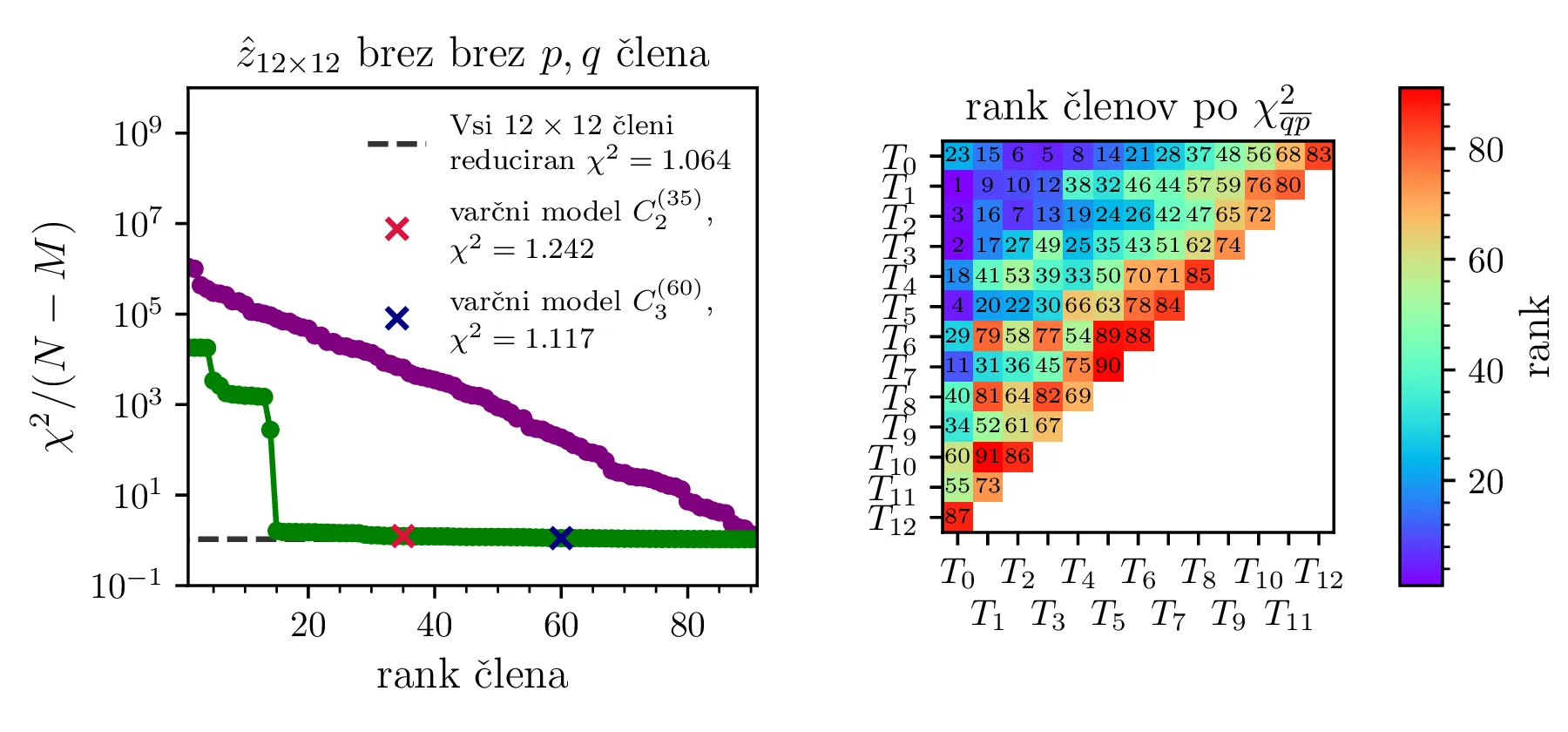
drugače. Prvo se spremeni korelacijska matrika med parametri (slika 10). Ob pogledu na sliki 13
pa izgleda, da z Chebyebishevo produktno bazo lažje dosežemo varčen model. Z zgolj 35 parametri dosežemo boljši
reducirani \(\chi^2\) kot z 60 parametri za navadno produktno polinomsko bazo.
Reševanje z SVD
Sam problem linearne regresije lahko preprosto rešujemo z uporabo SVD razcepa [1]. Rešitev za naš vektor parametrov \[\mathbf{c} = \begin{bmatrix} c_1 & c_2 & \dots & c_M \end{bmatrix}^T\] v smislu predoločenega sistema, kjer minimiziramo \[\| A\mathbf{c} - \mathbf{b}\|,\] kjer je \(\mathbf{b}\) vektor izmerkov, v našem primeru \(\vartheta_\mathrm{tg}^{(1)}, \vartheta_\mathrm{tg}^{(2)}, \dots, \vartheta_\mathrm{tg}^{(N)}\), je podana preko rešitve normalnega sistema \[A^T A \mathbf{c} = A^T \mathbf{b}.\] Tu si lahko pomagamo z SVD razcepom matrike \(A\) kot \[A = U \Sigma V^T,\] Kjer sta \(U\) in \(V\) ortogonalni, \(\Sigma\) pa diagonalna matrika. Po nekaj krajšega računanja lahko pokažemo, da je rešitev normalnega sistema tedaj podana v dveh korakih kot \[\begin{aligned} \text{1. korak: } &\Sigma \mathbf{w} = U^T \mathbf{b}, \text{reši sistem za }\mathbf{w}, \\ \text{2. korak: } &\mathbf{c} = V \mathbf{w}. \end{aligned}\] Dodatno velja tudi, da je kovariančna matrika podana kot \[\mathop{cov} \big( c_i, c_j \big) = V_{jk} V_{kj} / \Sigma_{kk}^2.\]
Iskanje varčnega modela z izločanjem členov
Cilj nam je poiskati model, ki potrebuje neko relativno majhno število parametrov, hkrati pa je dober glede na kriterij reduciranega \(\chi^2 \sim 1\). Da pridemo do takšnim modelov, bomo postopali sledeče
-
Za neko relativno visoko stopnjo \(K\), ki določa najvišji stopnji baze \(q + p \le K\), bomo z SVD razcepom rešili problem najmanjših kvadratov z \(M = \frac{1}{2} (K+1)(K+2)\) parametri.
-
(Brez ponovnega reševanja sistema) S postopkom maskiranja posameznih parametrov v modelu, kjer nastavimo nek \(c_i = 0\) določili hipotetične vrednosti \(\chi^2 (c_i = 0) / (N - M)\). Ko bomo takšne hipotetične \(\chi^2\) razporedili od največjega do najmanjšega, bo to naš t. i. "vrstni red dodajanja parametrov", mesto v tem vrstnem redu pa v nadaljevanju imenujemo rank. Tako padanje \(\chi^2 (c_i = 0) / (N - M)\) po ranku vidimo npr. na sliki 11 zgoraj levo v vijolični barvi.
-
(S ponovnim reševanja sistema) Za neko izbrano število prostih parametrov \(M\) bomo po "vrstnem red dodajanja parametrov" dodali le \(M\) parametrov, nato pa model na novo prilagodili v tej reducirani obliki. Tako padanje \(\chi^2/ (N - M)\) po ranku vidimo npr. na sliki 11 zgoraj levo v zeleni barvi.
Na tretjem koraku bomo dobili krivuljo, kjer s številom parametrov \(M\) reducirani \(\chi^2\) pada, a za višji rank se bolj ali manj ustali blizu \(1\). Tedaj je naša naloga, da tak model izberemo, upoštevajoč naše zahteve po malem številu parametrov oz. kvaliteti fita.
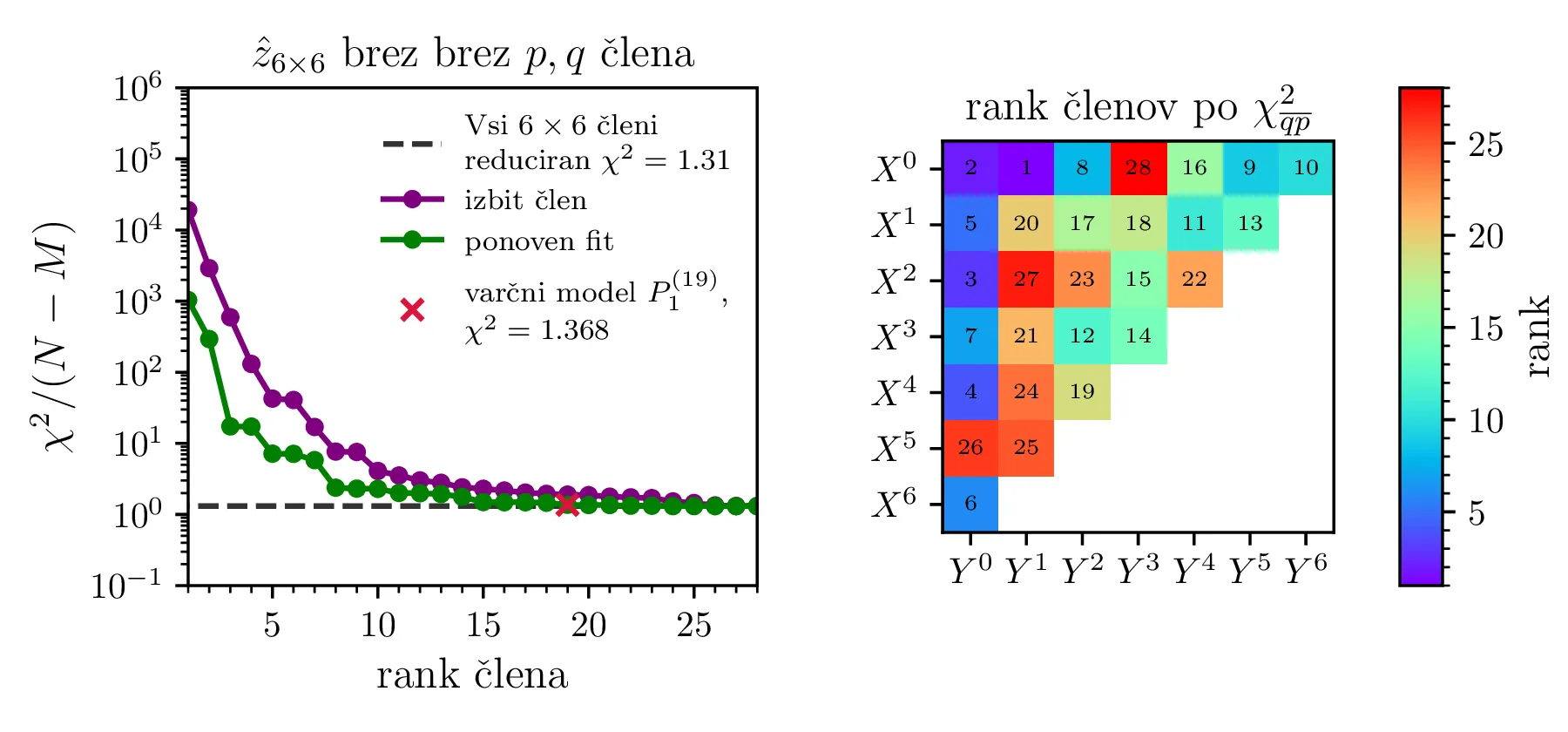
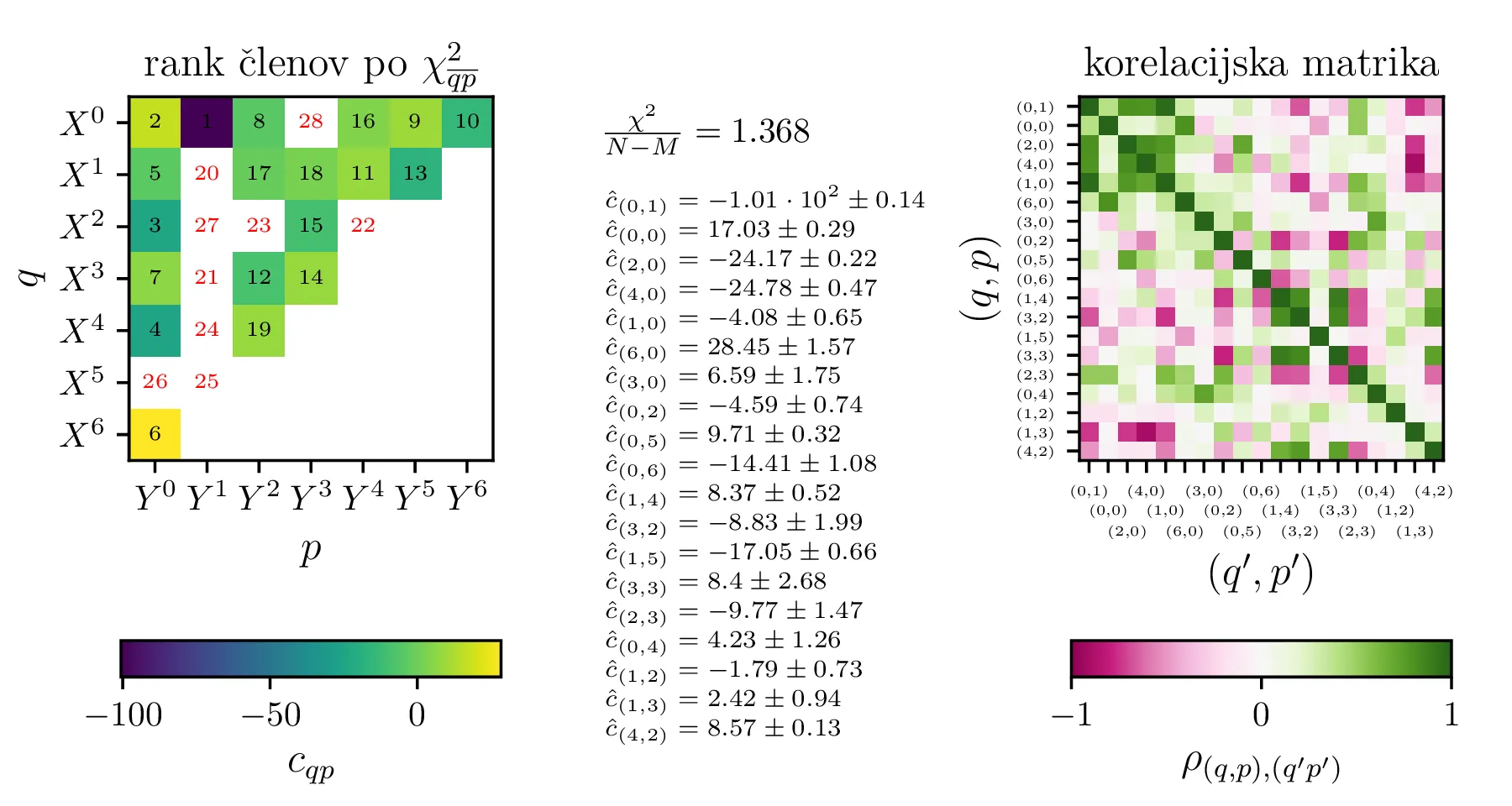
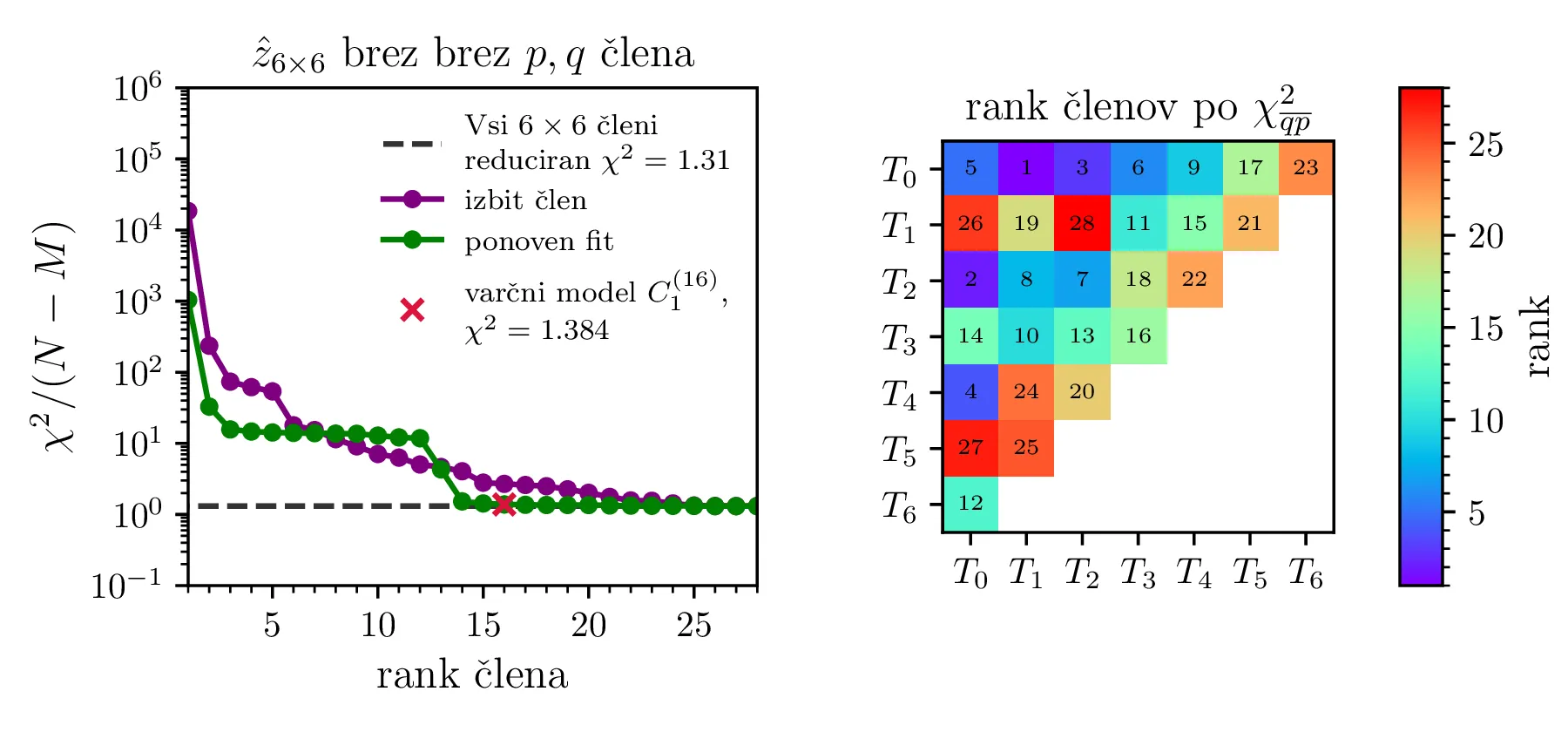
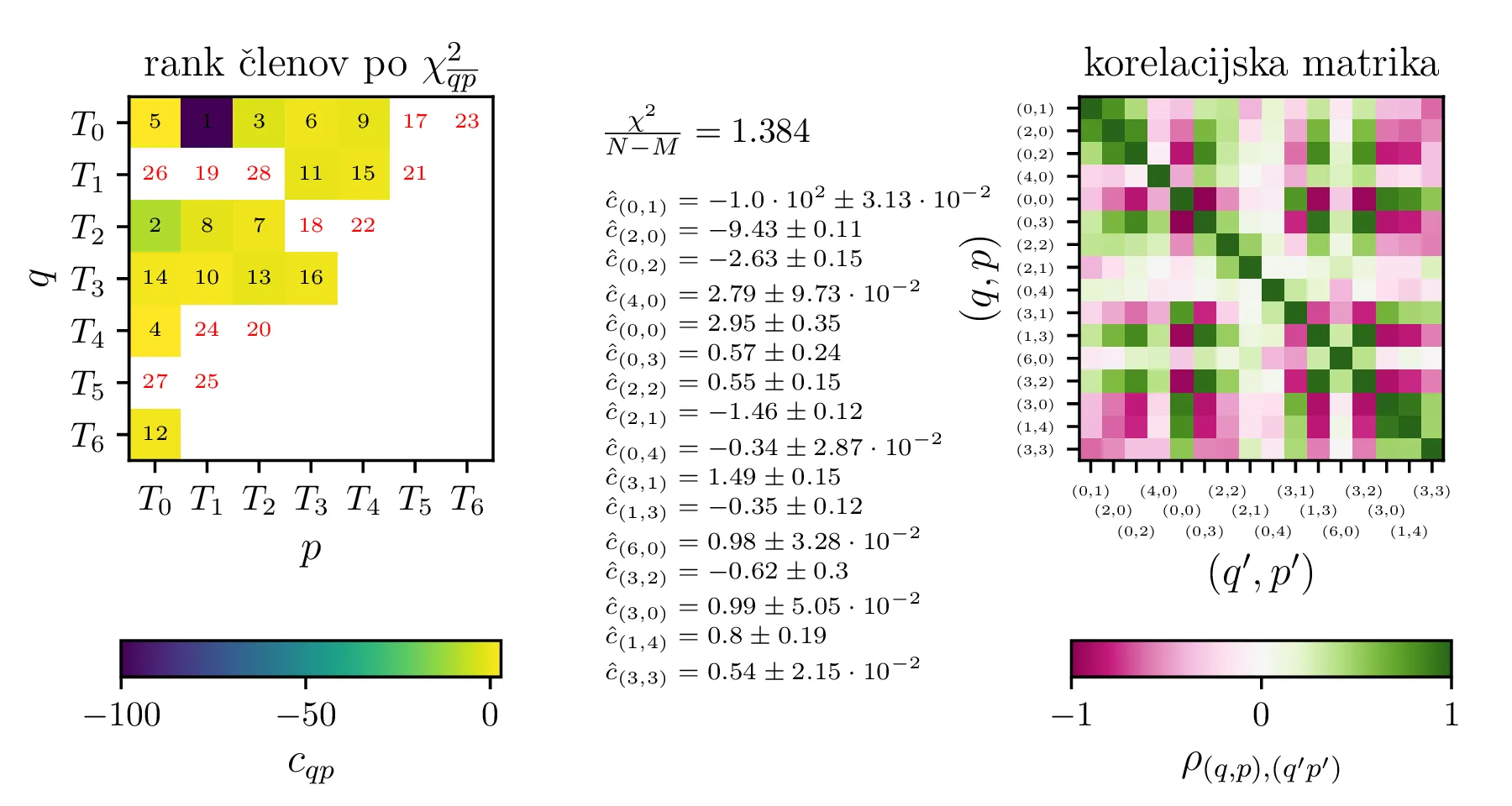
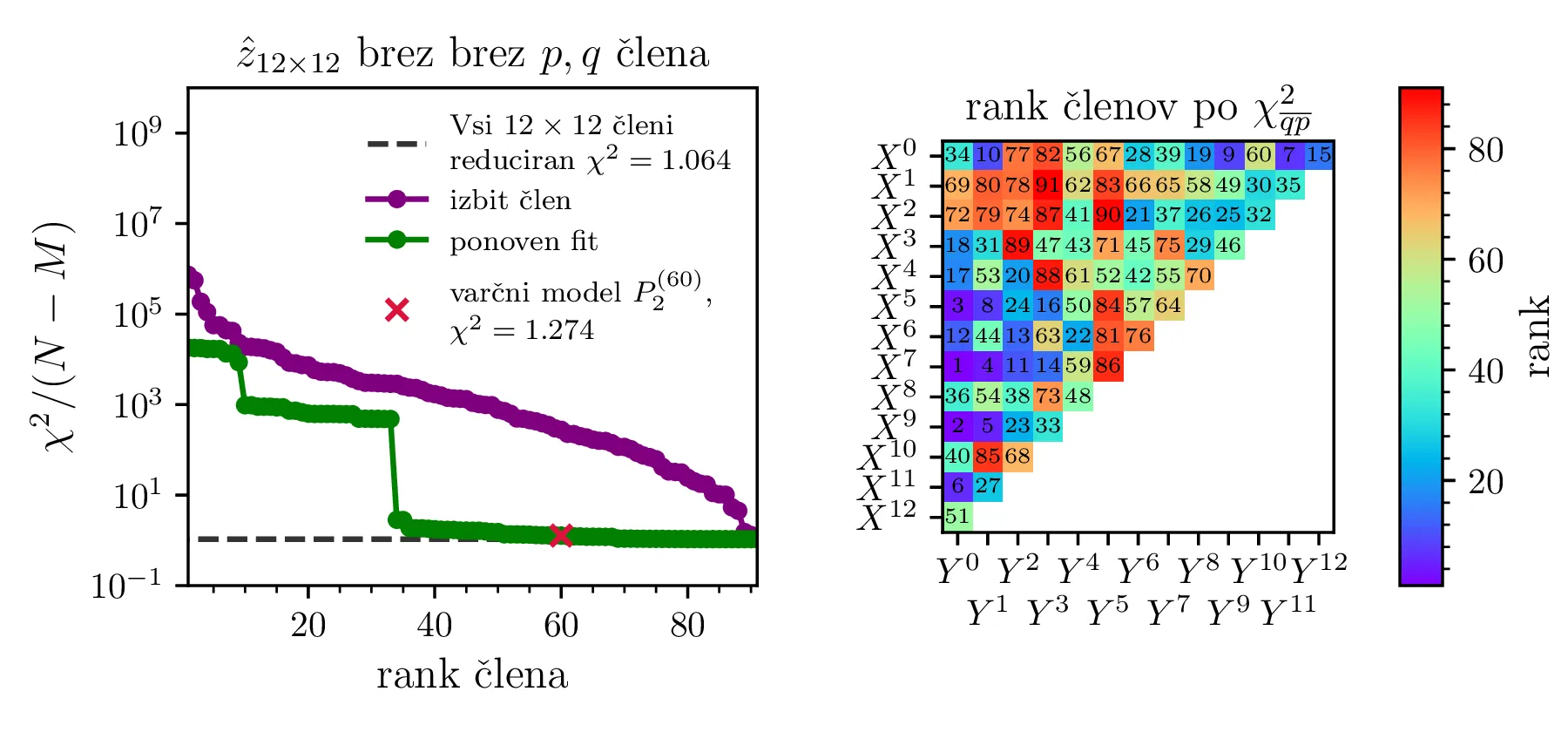
Po opisanem postopku obravnavamo modele z polinomsko \(X^q Y^p\) bazo do stopnje \(p + q \le K = 6\) na sliki 11. Na isti sliki 11 spodaj predstavimo tudi koeficiente in korelacijsko matriko za izbran varčni model \(P_1^{(16)}\) z 16 parametri. V primerjavo obravnavamo tudi modele s Chebyebishevo produktno bazo \(T_q(X) T_p(Y)\) do stopnje \(p + q \le K = 6\) na sliki 11. Na isti sliki spodaj predstavimo tudi varčni model \(C_1^{(13)}\) z 13 parametri.
Prednost baze \(T_q(X) T_p(Y)\) pa opazimo predvsem pri modelih z večjim \(K = 12\). Na sliki 13 primerjamo modela z navadno polinomsko in Chebyebishevo produktno bazo do stopnje \(K = 12\). S primerjavo zelenih krivulj ponovno prilagojenih modelov (sliki 13 zgoraj in spodaj levo) vidimo, da je model Chebyebishevo bazo hitreje varčen, dobro prileganje lahko doseže že z manjšim številom parametrov. Reducirani \(\chi^2\) za 60 parameterski polinomski model je namreč \(1.274\), za le 35 parameterski Chebyebishev model pa \(1.242\). Z 60 parametri, toliko kot jih ima polinomski model \(P_2^{(60)}\), pa Chebyebishev model doseže omembe vredno boljši reducirani \(\chi^2 = 1.117\).