Modelska analiza I
5. naloga: Modeli kemijskih reakcij

Navodila

Za model binarne reakcije \begin{equation}\begin{aligned} \mathrm{A} + \mathrm{A} &\mathop{\rightleftharpoons}_q^p \mathrm{A} + \mathrm{A}^*, \nonumber \\ \mathrm{A}^* &\mathop{\to}_r \mathrm{B} + \mathrm{C}, \label{eq:binary} \end{aligned}\end{equation} kjer je \(\frac{q}{p} = 1000\), integriraj sistem eksaktno in v aproksimaciji stacionarnega stanja za \(\frac{r}{q A(0)} \in \{ 10, 1, 0.1 \}\).
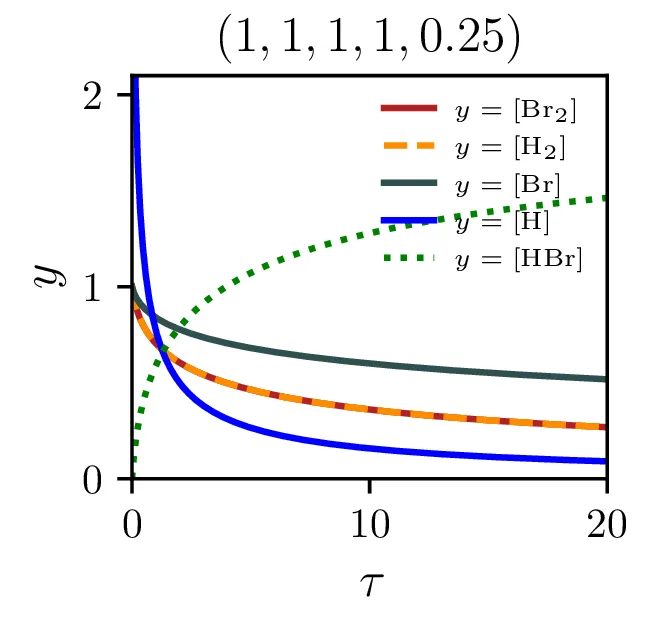
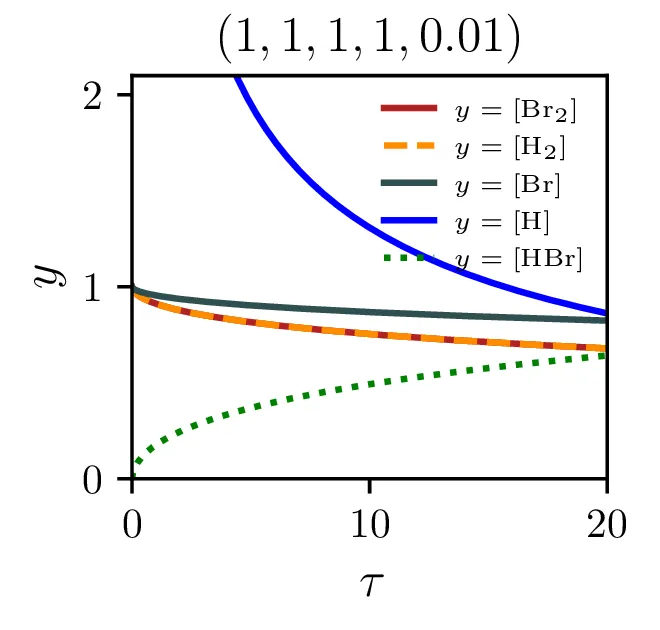
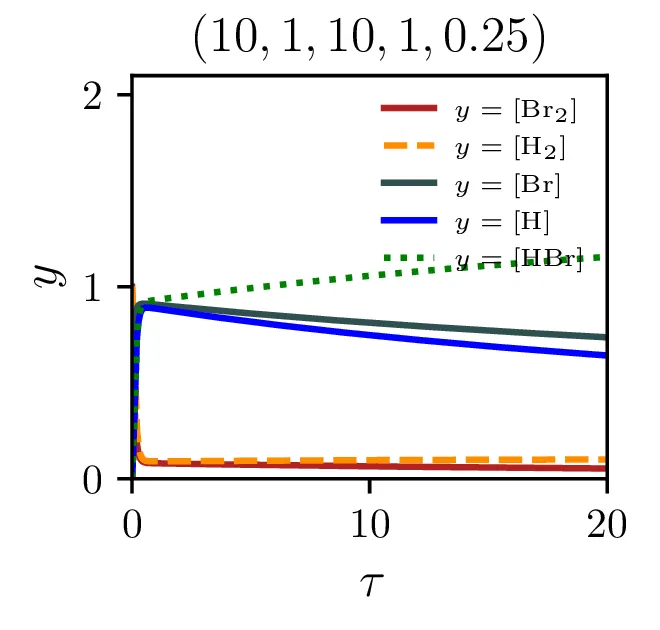
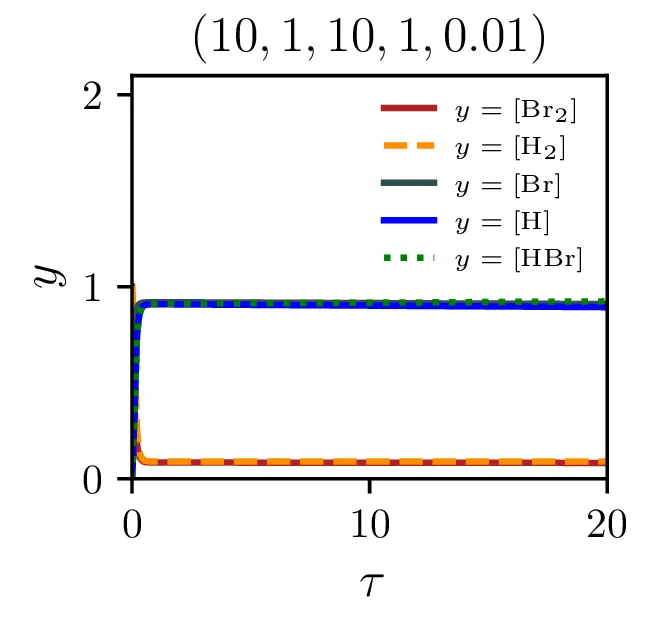
Model reakcije \(\mathrm{H}_2 + \mathrm{Br}_2 \rightleftharpoons 2\mathrm{HBr}\) vključuje naslednje stopnje: \begin{equation}\begin{aligned} &\mathrm{Br}_2 \mathop{\rightleftharpoons}_{\alpha'}^{\alpha} 2 \mathrm{Br}, \nonumber \\ &\mathrm{Br} + \mathrm{H}_2 \mathop{\rightleftharpoons}_{\beta'}^{\beta} \mathrm{HBr} + \mathrm{H}, \nonumber \\ &\mathrm{H} + \mathrm{Br}_2 \mathop{\to}_\xi \mathrm{HBr} + \mathrm{Br}. \label{eq:synthesis} \end{aligned}\end{equation} Določi hitrost sinteze \(\mathrm{HBr}\) v aproksimaciji stacionarnega stanja in primerjav z empiričnim izrazom \begin{equation}\mathop{[\mathrm{HBr}]}^\bullet = \frac{k[\mathrm{H}_2] [\mathrm{Br}_2]^{1/2}}{m + \frac{[\mathrm{HBr}]}{[\mathrm{Br}_2]}}. \label{eq:empiric}\end{equation} Kako bi najlažje izmeril empirični konstanti \(k\) in \(m\). Skiciraj časovne poteke za začetne \([\mathrm{H}_2]/[\mathrm{Br}_2] \in \{ 100, 1, 0.01 \}\) in \(m = 2.5\). Ali kaj pomaga, če že v začetno stanje primešamo mnogo \(\mathrm{HBr}\).
Kemijske ure so reakcije, ki stečejo s predvidljivim in ponavadi ostrim časovnim zamikom. Primer take reakcije je jodova ura, ki v eni izmed izvedb temelji na ravnotežju naslednjih reakcij: \begin{equation}\begin{aligned} \mathrm{S_{2}O_{8}^{2-}} + 2\mathrm{I^{-}}&\mathop{\to}_\delta \mathrm{I_2}+ 2\mathrm{SO_4^{2-}}, \nonumber \\ 2\mathrm{S_{2}O_{3}^{2-}} + \mathrm{I_2}&\mathop{\to}_{\delta'} 2\mathrm{I^{-}}+ \mathrm{S_{4}O_{6}^{2-}}. \label{eq:clock} \end{aligned}\end{equation} Druga reakcija je bistveno hitrejša od prve, mehanizem merjenja časa pa je enakomerno porabljanje tiosulfata \(\mathrm{S_2O_3^{2-}}\). Če je persulfat \(\mathrm{S_2O_8^{2-}}\) v prebitku, lahko za aktivne spremenljivke vzamemo le \([\mathrm{I^{-}}]\), \([\mathrm{I_2}]\) in \(\mathrm{S_{2}O_{3}^{2-}}\). Obe zgornji reakciji sta v resnici sestavljeni iz še dveh stopenj. Prva reakcija je sestavljena iz stopenj \begin{equation}\begin{aligned} &\mathrm{S_{2}O_{8}^{2-}} + \mathrm{I^{-}}\mathop{\to}_\text{počasi} \mathrm{I}\mathrm{S_{2}O_{8}^{3-}},\nonumber \\ &\mathrm{I}\mathrm{S_{2}O_{8}^{2-}} + \mathrm{I^{-}}\mathop{\to}_\text{hitro} \mathrm{I_2}+ 2\mathrm{SO_4^{2-}}, \label{eq:clock-A} \end{aligned}\end{equation} druga reakcija pa iz stopenj \begin{equation}\begin{aligned} &\mathrm{S_{2}O_{8}^{2-}} + \mathrm{I^{-}}\mathop{\to}_\text{počasi} \mathrm{I}\mathrm{S_2O_3^-} + \mathrm{I^{-}}, \nonumber \\ &\mathrm{I}\mathrm{S_2O_3^-} + \mathrm{S_{2}O_{3}^{2-}} \mathop{\to}_\text{hitro} \mathrm{I^{-}}+ \mathrm{S_{4}O_{6}^{2-}}. \label{eq:clock-B} \end{aligned}\end{equation} Izpelji glavni kinetični zvezi v približku stacionarnega stanja. Razišči potek celotne reakcije in odvisnost trajanja reakcije od začetne koncentracije tiosulfata. Za razmerje hitrosti glavnih reakcij vzemi \(\delta'/\delta \in \{1, 10, 100\}\).

Binarna reakcija

Za model binarne reakcije lahko zapišemo sistem navadnih diferencialnih enačb \begin{equation}\begin{aligned} &\dot{A} = -p AA + q A A^*, \nonumber \\ &\dot{A}^* = p AA - q A A^* - r A^*, \nonumber \\ &\dot{B} = rA^*, \nonumber \\ &\dot{C} = rA^*. \label{eq:nde-binary} \end{aligned}\end{equation} Da namesto treh parametrov \(p, q, r\) operiramo z dvema parametroma \[\gamma \vcentcolon=\frac{q}{p}, \quad \mu \vcentcolon=\frac{r}{p},\] lahko sistem zapišemo za brezdimenzijski čas \(\tau = pt\), tako da je \(\dot{x} = \frac{\mathrm{d}x}{\mathrm{d}\tau}\), ne \(\frac{\mathrm{d}x}{\mathrm{d}t}\). Oblika sistema je tedaj \begin{equation}\begin{aligned} &\dot{A} = -AA + \gamma A A^*, \nonumber \\ &\dot{A}^* = AA - \gamma A A^* - \mu A^*, \nonumber \\ &\dot{B} = \mu A^*, \nonumber \\ &\dot{C} = \mu A^*. \label{eq:nde-binary-nondim} \end{aligned}\end{equation}

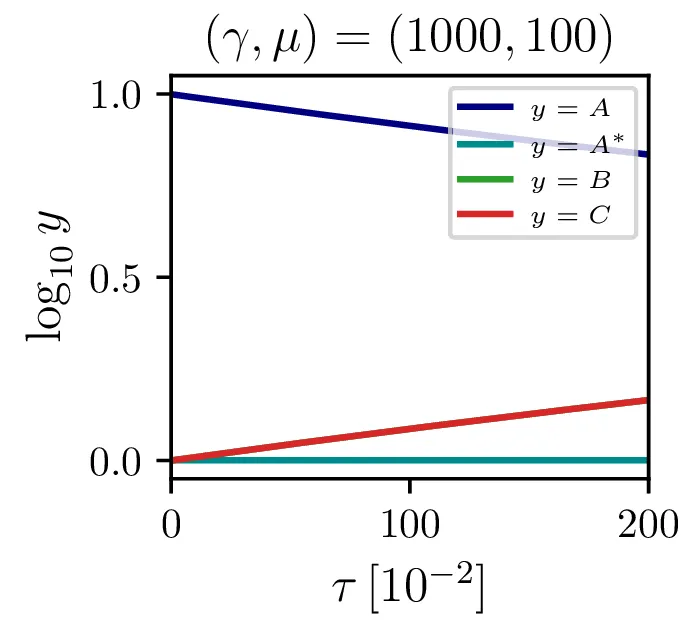
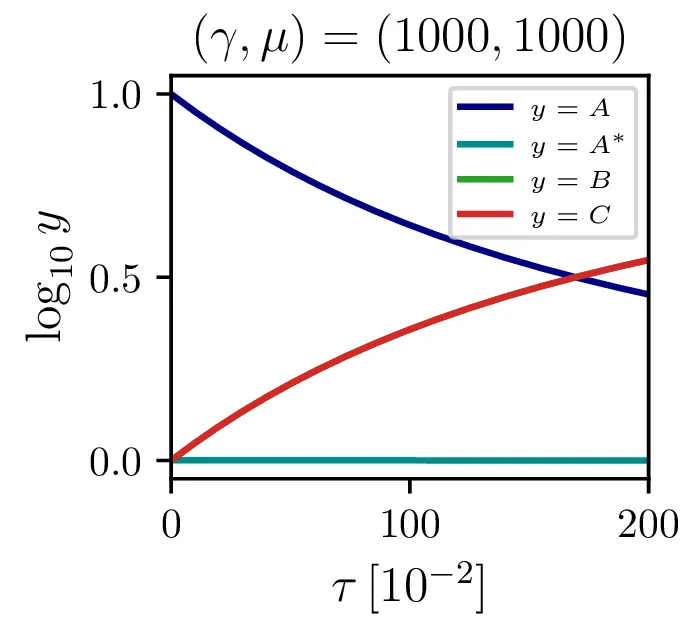
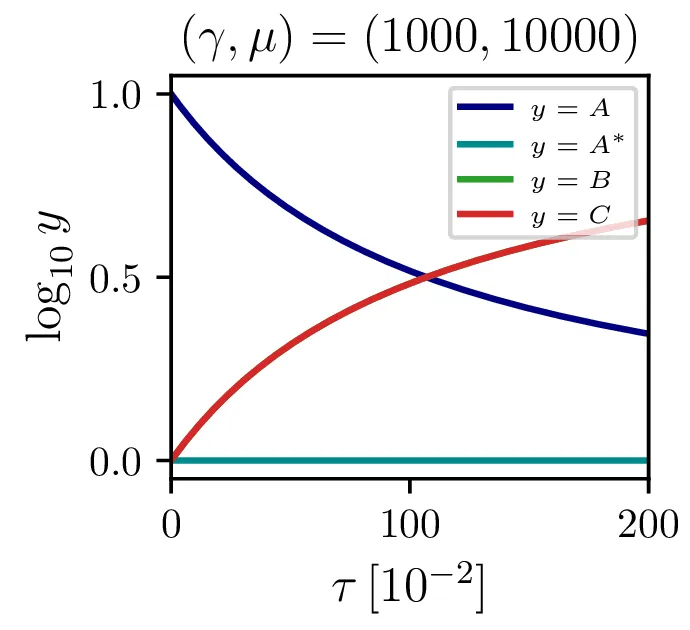
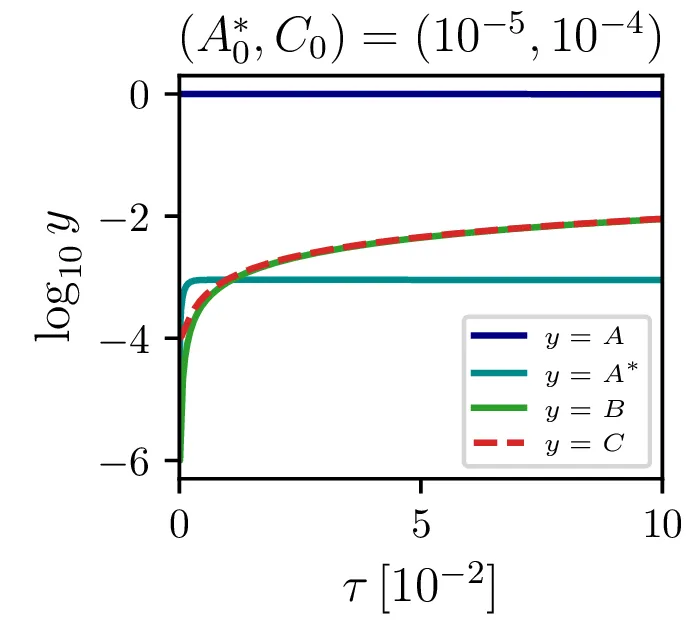
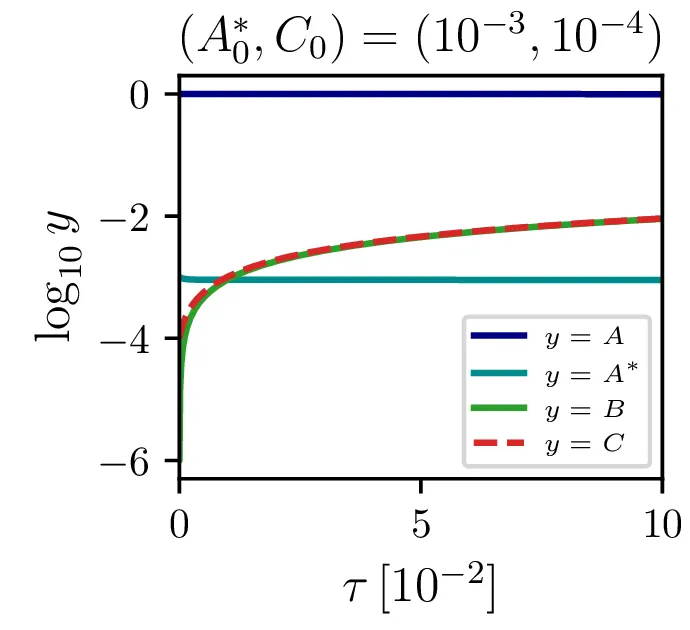
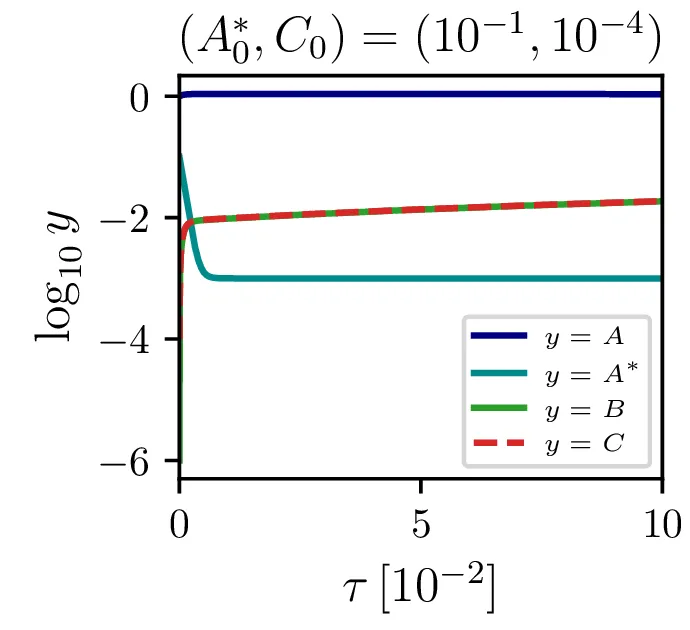
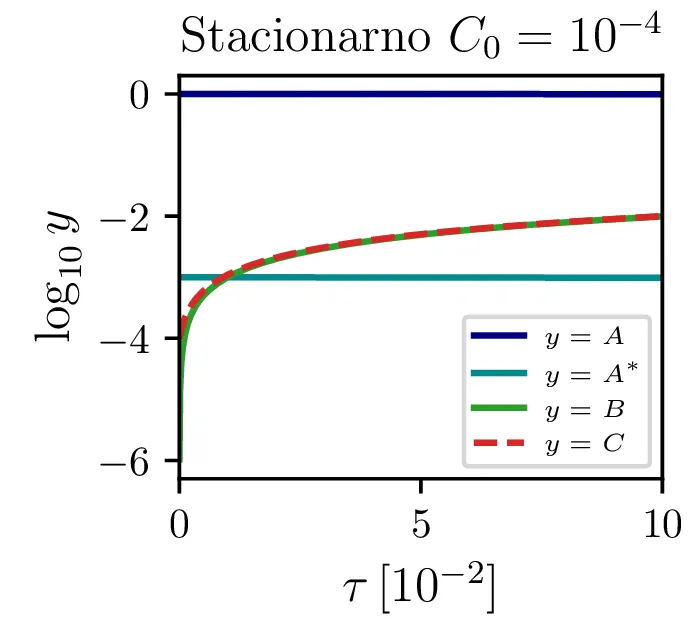
Poteki za \(\tau \in [0, 2]\), \(A(0) = 1\), \(\gamma = 1000\) in različne \(\frac{r}{qA(0)}\). (Levo) \(\frac{r}{qA(0)} = 0.1\) oziroma \(\mu = 100\). (Sredinsko) \(\frac{r}{qA(0)} = 1\) oziroma \(\mu = 1000\). (Desno) \(\frac{r}{qA(0)} = 10\) oziroma \(\mu = 10^4\).

Sistem (8) rešimo za \(\gamma = 1000\) in \(\frac{r}{q A(0)} \in \{ 10, 1, 0.1 \}\) na sliki 1. Vidimo, da večji \(\mu\) kot pričakovano pomeni hitrejši potek reakcije.

Stacionarni približek

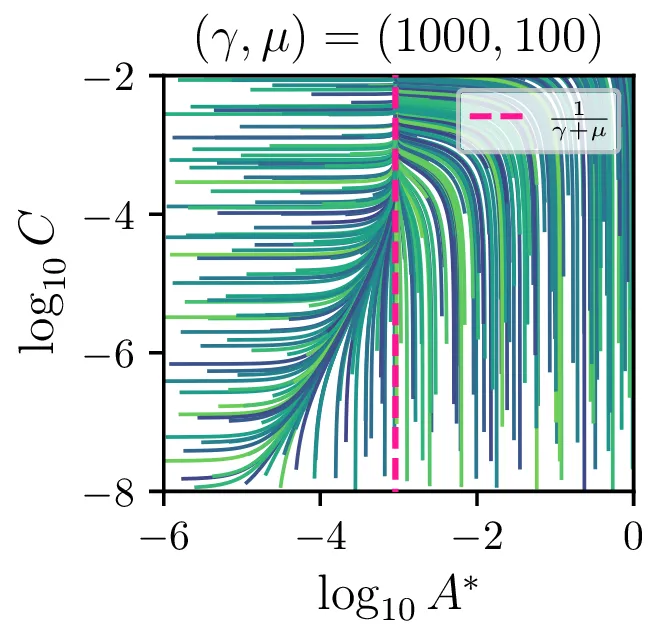
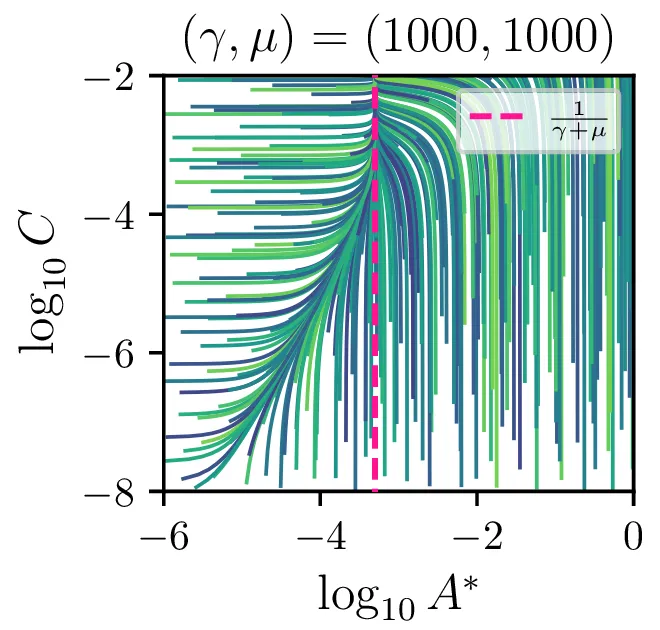
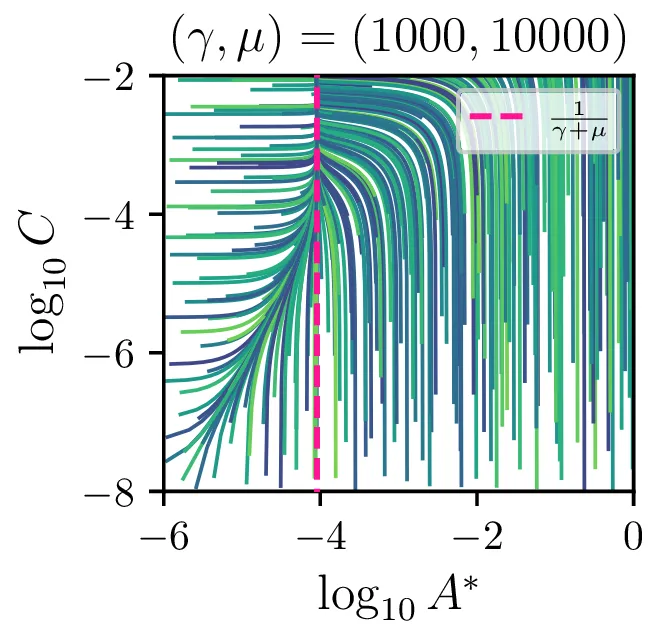
Poteki za \(\tau \in [0, 10^{-2}]\) in začetne pogoje \((A, A^*, B, C)_0 = (1, A^*_0, 0, C_0)\). Parameter \(\gamma\) je vseskozi \(1000\), narisani pa so različni \(\mu\). (Levo) \(\mu = 100\). (Sredinsko) \(\mu = 1000\). (Desno) \(\mu = 10^4\).

Sistem diferencialnih enačb se znatno poenostavi, če predpostavimo stacionarnost \(\dot{A}^* \approx 0\). Tedaj velja \[AA = \gamma AA^* + \mu A^*,\] in sistem diferencialnih enačb (8) se poenostavi v \begin{equation}\begin{aligned} &\dot{A} = -\mu A^*, \nonumber \\ &\dot{B} = \mu A^*, \nonumber \\ &\dot{C} = \mu A^*, \label{eq:nde-binary-stationary} \end{aligned}\end{equation} zraven pa za \(A^*\) velja \[A^* = \frac{A^2}{\gamma A + \mu}.\]

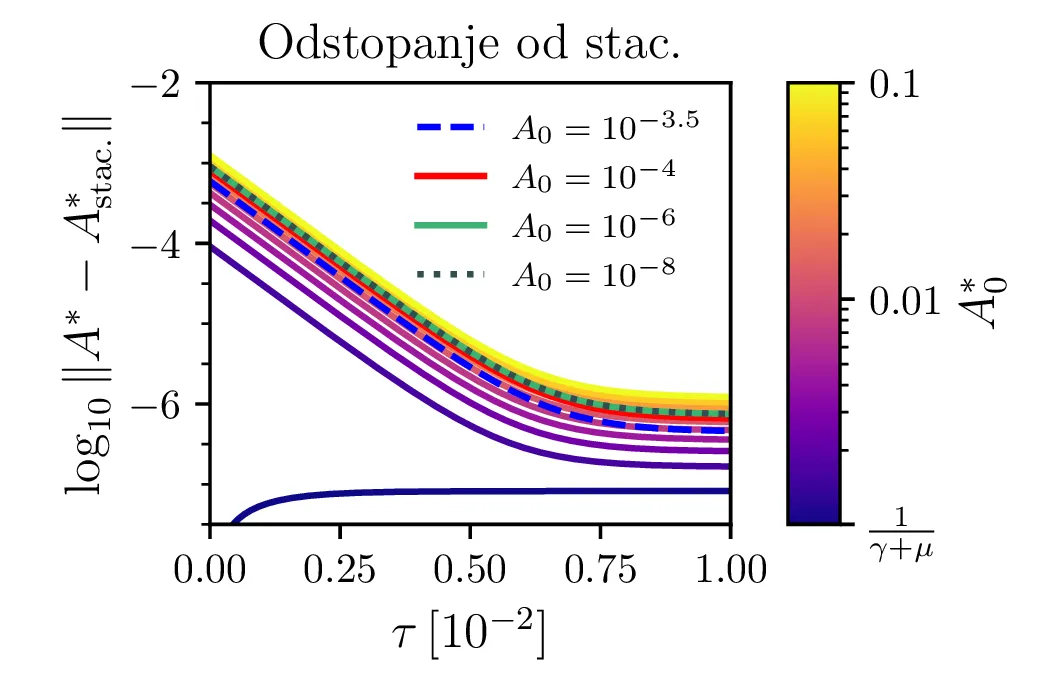
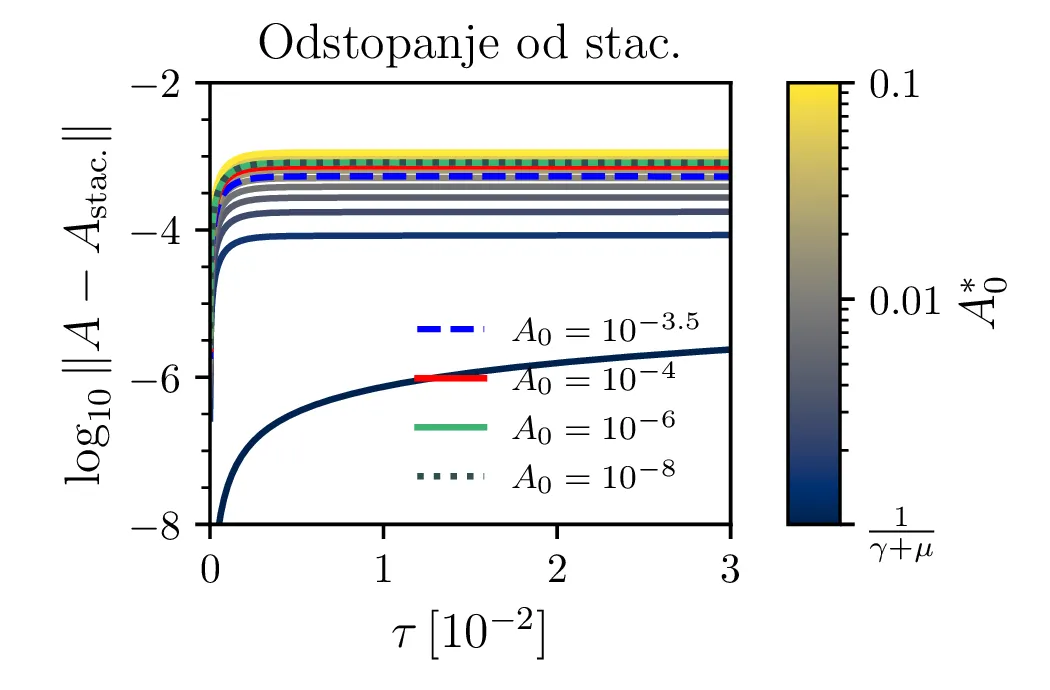
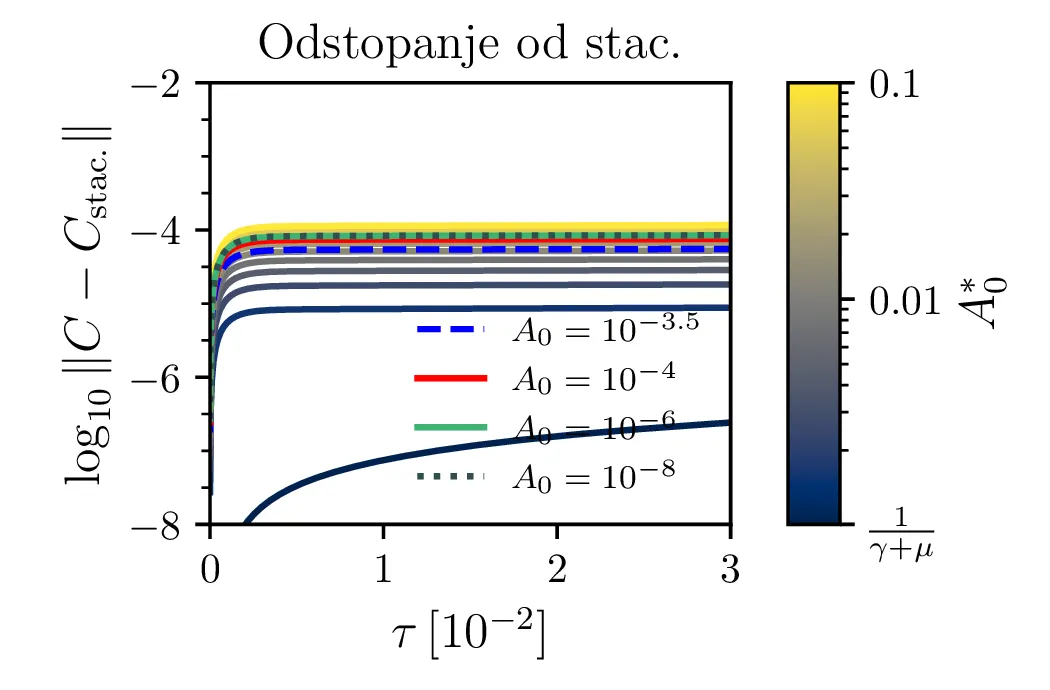
Glavno vprašanje je, kdaj je tak približek smiseln. Na to vprašanje nam najlažje pomagajo odgovoriti fazni diagrami 2. Na njih jasno vidimo, da se \(A^*\) za vse poteke bliža nekakšni "dolini", v kateri je \(A^* = \text{konst.}\). Asimptotsko obnašanje torej dobro opiše predpostavka \(\dot{A}^* \approx 0\) in sistem enačb (9). Na sliki 4 levo vidimo rešitev v takšnem, stacionarnem približku. Kvantitativno primerjavo oz. odstopanje od eksaktne rešitve narišemo na sliki 4 desno in na sliki 4.

(Levo) Potek v približku stacionarnega \(A^*\). Če potek primerjamo z sliko 3 desno, je potek vizualno podoben, razlikuje se le v začetnem ostrem padcu \(A^*\). (Desno) Odstopanje stacionarnega približka \(A^*_\mathrm{stac.}\) in eksaktne rešitve. Narisana so odstopanje za različne začetne pogoje \(A^*_0\), kot za premico v faznem diagramu 2 levo. Vidimo, da je odstopanje najmanjše ravno za

Odstopanje stacionarnega približka od eksaktne rešitve. (Levo) Odstopanje \(A\). (Desno) Odstopanje \(C\).

Sinteza HBr

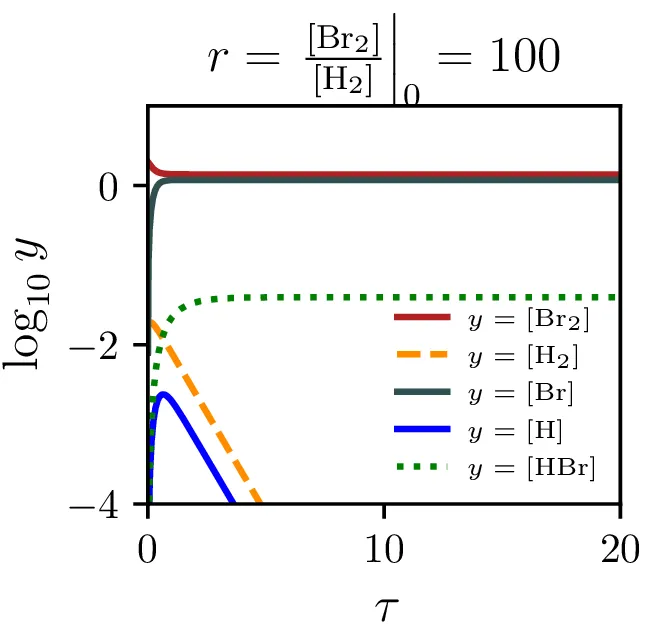
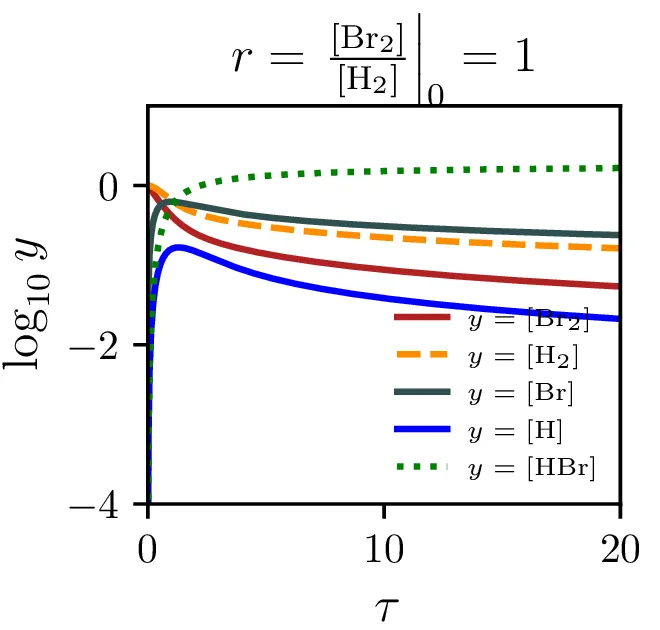
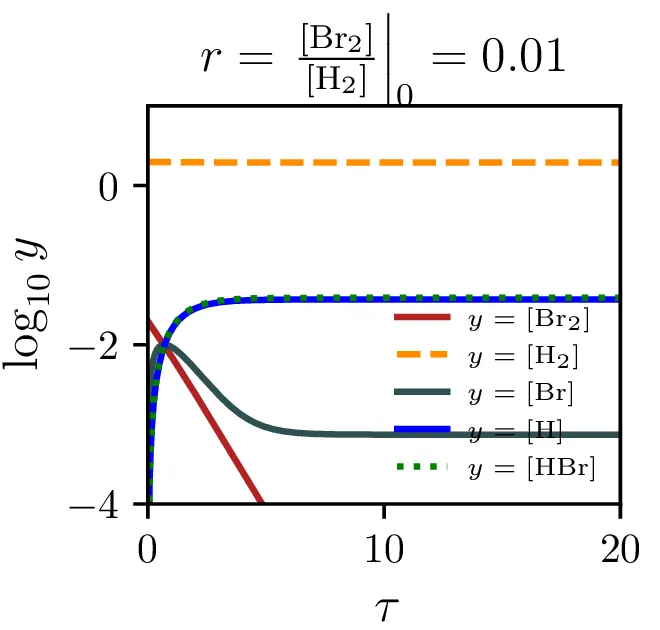
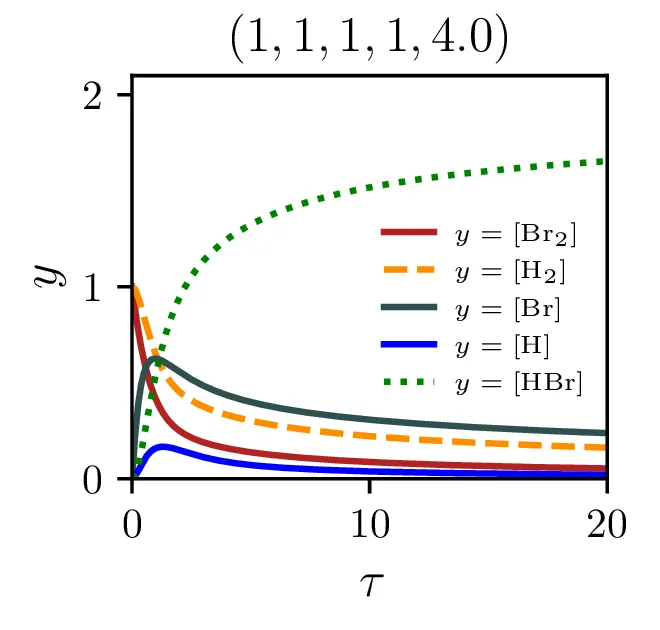
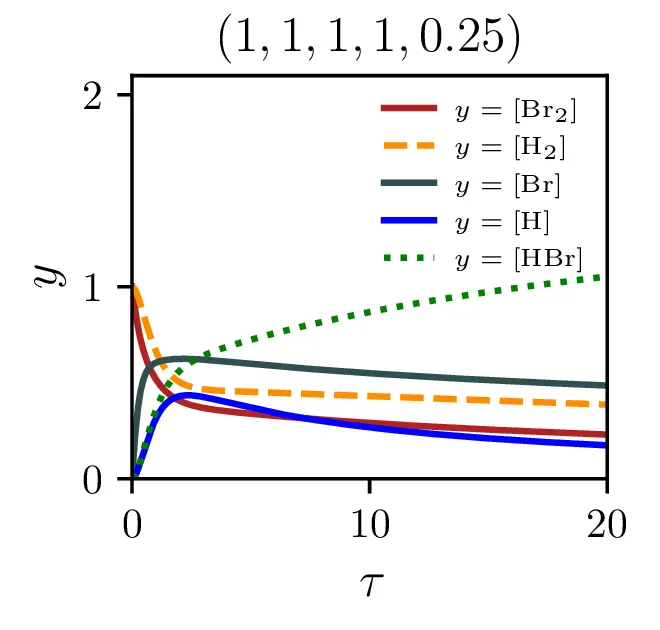
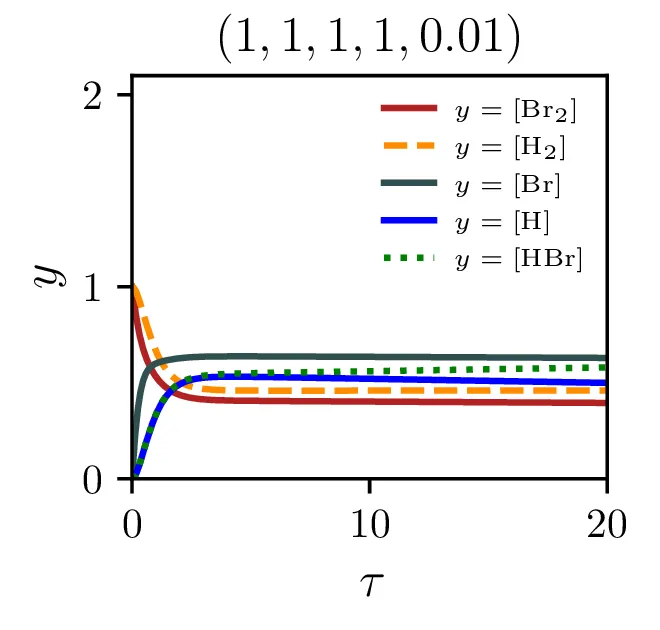
Sintezo \(\mathrm{HBr}\), ki jo opisuje reakcija 2, lahko opišemo s sistemom diferencialnih enačb \begin{equation}\begin{aligned} &\mathop{[\mathrm{Br}_2]}^\bullet = \Big( -\alpha [\mathrm{Br}_2] + \alpha' [\mathrm{Br}][\mathrm{Br}] \Big) - \xi [\mathrm{H}][\mathrm{Br}_2], \nonumber \\ &\mathop{[\mathrm{H}_2]}^\bullet = - \beta [\mathrm{Br}][\mathrm{H}_2] + \beta' [\mathrm{HBr}][\mathrm{H}], \nonumber \\ &\mathop{[\mathrm{Br}]}^\bullet = 2\Big( \alpha [\mathrm{Br}_2] - \alpha' [\mathrm{Br}] [\mathrm{Br}] \Big) - \Big( \beta [\mathrm{Br}][\mathrm{H}_2] - \beta' [\mathrm{HBr}][\mathrm{H}] \Big) + \xi [\mathrm{H}] [\mathrm{Br}_2], \nonumber \\ &\mathop{[\mathrm{H}]}^\bullet = \Big( \beta [\mathrm{Br}][\mathrm{H}_2] - \beta' [\mathrm{HBr}][\mathrm{H}] \Big) - \xi [\mathrm{H}][\mathrm{Br}_2], \nonumber \\ &\mathop{[\mathrm{HBr}]}^\bullet = \Big( \beta [\mathrm{Br}][\mathrm{H}_2] - \beta' [\mathrm{HBr}][\mathrm{H}] \Big) + \xi [\mathrm{H}][\mathrm{Br}_2]. \label{eq:synthesis-system} \end{aligned}\end{equation} Rešitve sistema enačb (10) za različne začetne pogoje predstavimo na sliki 6. Kot pričakovano je količina nastalega \(\mathrm{HBr}\) največja pri reakciji, v katero dodatno reaktanta \(\mathrm{Br}_2, \mathrm{H}_2\) v enakem razmerju.

Poteki za \(\tau \in [0, 20]\) in parametre \((\alpha, \alpha', \beta, \beta', \xi) = (1, 1, 1, 1, 4)\). Različni so začetni pogoji \(([\mathrm{Br}_2], [\mathrm{H}_2], [\mathrm{Br}], [\mathrm{H}], [\mathrm{HBr}])_0 = (\frac{2r}{r+1}, \frac{2}{r+1}, 0, 0, 0)\). (Od leve proti desni) Poteki, ki jih dobimo z integracijo sistema (10) za \(r = \left. \frac{[\mathrm{Br}_2]}{[\mathrm{H}_2]} \right\vert_0 \in \{ 100, 1, 1/100 \}\).

Stacionarnost vmesnih produktov

Za vmesna produkta \(\mathrm{Br}\) in \(\mathrm{H}\) bomo predpostavili, da je njuna koncentracija konstanta. Če velja \([\mathrm{Br}] = 0\) in \([\mathrm{H}] = 0\), lahko iz enačb za ta dva produkta v sistemu (10) zapišemo \begin{equation}\begin{aligned} 0 = \alpha [\mathrm{Br}_2] - \alpha' [\mathrm{Br}][\mathrm{Br}]. \label{eq:lemma-br} \end{aligned}\end{equation} Sistem (10) za 5 spremenljivk se v stacionarnem približku prevede na sistem za \((\mathrm{Br}_2, \mathrm{H}_2, \mathrm{HBr})\). Ob upoštevanju (11) lahko iz diferencialne enačbe za \(\mathop{[\mathrm{H}]}^\bullet\) zapišemo \begin{equation}[\mathrm{H}] = \frac{\beta \sqrt{\frac{\alpha}{\alpha'} [\mathrm{Br}_2]} \cdot [\mathrm{H}_2]}{\beta' [\mathrm{HBr}] + \xi [\mathrm{Br}_2]}. \label{eq:H-stac}\end{equation} Rekonstruirati želimo izraz za hitrost sinteze \(\mathrm{HBr}\) in ga primerjati z empiričnim izrazom (3). To je pravzaprav zadnja diferencialna enačba v sistemu (10), v stacionarnem približku \[\begin{aligned} \mathop{[\mathrm{HBr}]}^\bullet &= \left( \beta [\mathrm{H}_2] \sqrt{\frac{\alpha}{\alpha'} [\mathrm{Br}_2]} - \beta' [\mathrm{HBr}] [\mathrm{H}_2] \frac{\beta \sqrt{\frac{\alpha}{\alpha'} [\mathrm{Br}_2]}}{\beta' [\mathrm{HBr}] + \xi [\mathrm{Br}_2]} \right) + \xi [\mathrm{Br}_2] [\mathrm{H}_2] \frac{\beta \sqrt{\frac{\alpha}{\alpha'} [\mathrm{Br}_2]}}{\beta' [\mathrm{HBr}] + \xi [\mathrm{Br}_2]} \\ &= \beta [\mathrm{H}_2] \sqrt{\frac{\alpha}{\alpha'} [\mathrm{Br}_2]} \left( 1 - \frac{1}{[\mathrm{HBr}] + \frac{\xi}{\beta'} [\mathrm{Br}_2]} + \frac{\frac{\xi}{\beta'} [\mathrm{Br}_2]}{[\mathrm{HBr}] + \frac{\xi}{\beta'}[\mathrm{Br}_2]} \right), \\ \end{aligned}\] iz česar dobimo izraz \begin{equation}\mathop{[\mathrm{HBr}]}^\bullet = \left( \frac{2\beta \xi}{\beta'} \sqrt{\frac{\alpha}{\alpha'}} \right) \frac{[\mathrm{H}_2] \sqrt{[\mathrm{Br}_2]}}{\frac{\xi}{\beta'} + \frac{[\mathrm{HBr}]}{[\mathrm{Br}_2]}}, \label{eq:stac-hbr}\end{equation} ki je enake oblike kot empirični zakon (3), le za konstanti \[k = \frac{2\beta \xi}{\beta'} \sqrt{\frac{\alpha}{\alpha'}}, \qquad m = \frac{\xi}{\beta'}.\] Tako kot smo zapisali \([\mathrm{HBr}]^\bullet\) v (13), lahko zapišemo tudi za \(\mathrm{Br}_2\) in \(\mathrm{H_2}\). Celotni sistem enačb v stacionarnem približku se tedaj glasi \begin{equation}\begin{aligned} &\mathop{[\mathrm{Br}_2]}^\bullet = -\frac{k}{2} \cdot \frac{[\mathrm{H}_2] \sqrt{[\mathrm{Br}_2]}}{m + \frac{[\mathrm{HBr}]}{[\mathrm{Br}_2]}}, \nonumber \\ &\mathop{[\mathrm{H}_2]}^\bullet = - \frac{k}{2} \cdot \frac{[\mathrm{H}_2] \sqrt{[\mathrm{Br}_2]}}{m + \frac{[\mathrm{HBr}]}{[\mathrm{Br}_2]}}, \nonumber \\ &\mathop{[\mathrm{HBr}]}^\bullet = k \cdot \frac{[\mathrm{H}_2] \sqrt{[\mathrm{Br}_2]}}{m + \frac{[\mathrm{HBr}]}{[\mathrm{Br}_2]}}. \label{eq:synthesis-system-stac} \end{aligned}\end{equation}

Odstopanje stacionarnega približka od eksaktne rešitve. Parametri \(\alpha, \alpha', \beta, \beta'\) so stalno enaki \(1\) (Od leve proti desni) Parameter \(\xi \in \{ 4, 1/4, 1/100 \}\). Z različnimi barvami so narisana odstopanja za različna začetna razmerja \(r = \left. \frac{[\mathrm{Br}_2]}{[\mathrm{H}_2]} \right\vert_0\). Na levi sliki jasno vidimo, da je odstopanje največje ravno za \(r \approx 1\).

(Levo) Izkupiček sinteze \(\mathrm{HBr}\), prikazan kot koncentracija \(HBr\) po dolgem času \(\tau = 100\). Prikazana je odvisnost izkupička od začetnega razmerja reaktantov \(r = \left. \frac{[\mathrm{Br}_2]}{[\mathrm{H}_2]} \right\vert_0\). Parametri \(\alpha, \alpha', \beta, \beta\) so vsi enaki \(1\), za različne \(\xi\) so krivulje izkupička \(r\) narisane v različnih barvah. (Desno) Izkupiček z neničelnimi začetnimi koncentracijami \([\mathrm{HBr}]_0 > 0\) in \(\xi = 4\). Narisan je presežni izkupiček, torej koliko \([\mathrm{HBr}] - [\mathrm{HBr}]_0\) smo pridobili na koncu sinteze. Vidimo, da dodatek \(\mathrm{HBr}\) poslabša izkupiček reakcije.

Problematičnost stacionarnega približka

Tak stacionaren približen povsem formalno ni povsem smiseln, saj iz enačbe (11) takoj sledi, da mora pri stacionarnem \([\mathrm{Br}]\) biti stacionaren tudi \([\mathrm{Br}_2]\), tako pa je edina rešitev trivialna rešitev, kjer so vse koncentracije v sistemu konstantne. Tako moramo stacionarnost razumeti v nekakšnem bolj ohlapnem smislu. Kako točno bi to formaliziral nisem prepričan.

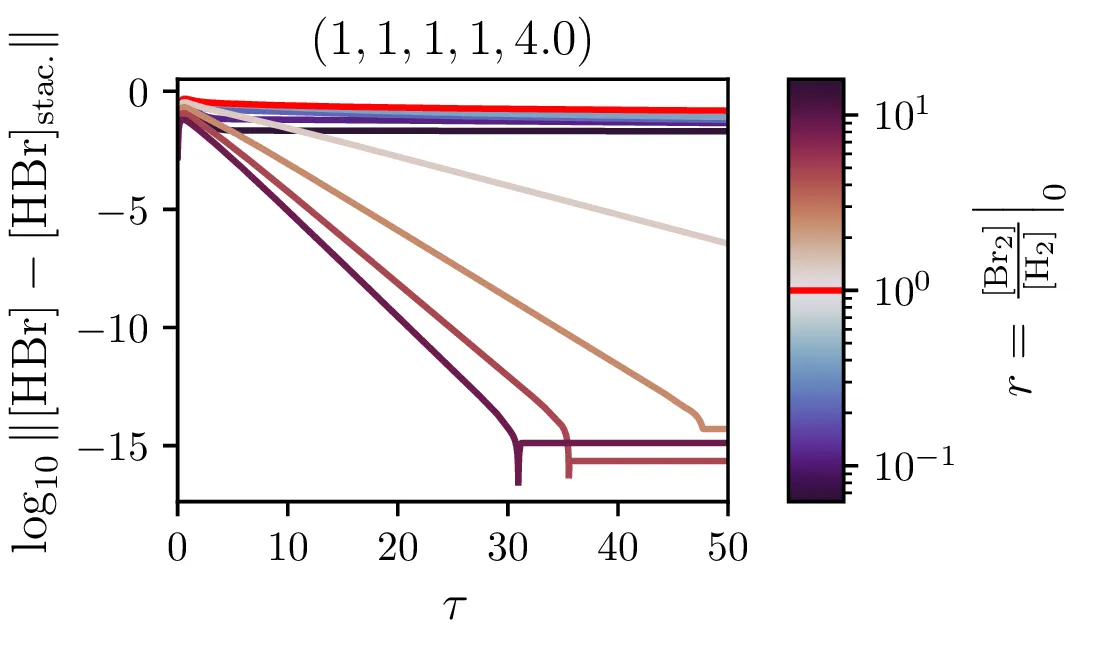
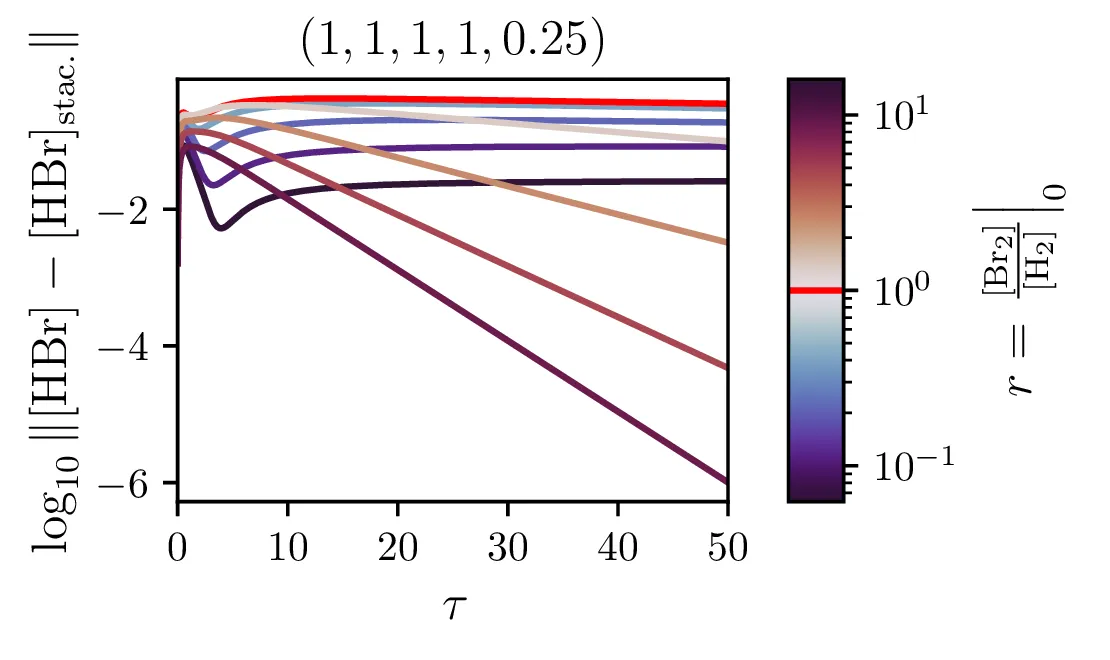
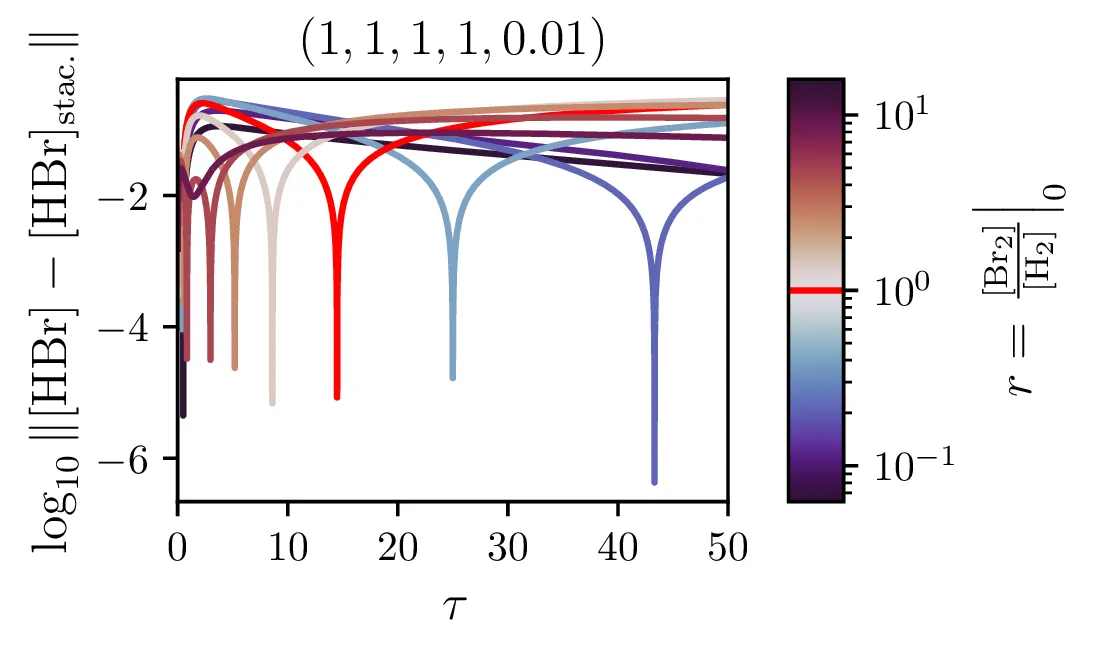
Kljub paradoksalnosti stacionarnega približka, za katerega velja \(\mathop{[\mathrm{Br}]}^\bullet = 0\) ob izpeljavi sistema (14), ne velja pa \(\mathop{[\mathrm{Br}]}^\bullet = 0\) tudi za rešitve (npr. na sliki 9 spodaj), je približek uporaben. Kako sam potek \([\mathrm{HBr}]\) v stacionarnem približku odstopa od eksaktne rešitve, lahko vidimo na sliki 7. Ta odstopanja so največja ob začetnem času in za začetna razmerja reaktantov \(\sim 1\) (kjer ima reakcija najboljši izkupiček, glej sliko 8). Poleg tega lahko sami hitrostni parametri reakcije naredijo približek zelo slab (primerjaj na sliki 9 spodaj in zgoraj)

Poteki za \(\tau \in [0, 20]\) in začetne pogoje \(([\mathrm{Br}_2], [\mathrm{H}_2], [\mathrm{Br}], [\mathrm{H}], [\mathrm{HBr}])_0 = (1, 1, 0, 0, 0)\). Parametri \(\alpha, \alpha', \beta, \beta'\) so vsi enaki \(1\), spreminjamo le hitrost \(\xi\). (Zgoraj od leve proti desni) Poteki, ki jih dobimo z integracijo sistema (10) za \(\xi \in \{ 4, 1/4, 1/100 \}\). (Zgoraj od leve proti desni) Poteki v stacionarnem približku (sistem (14) za \(\xi \in \{ 4, 1/4, 1/100 \}\).

Izkupiček sinteze

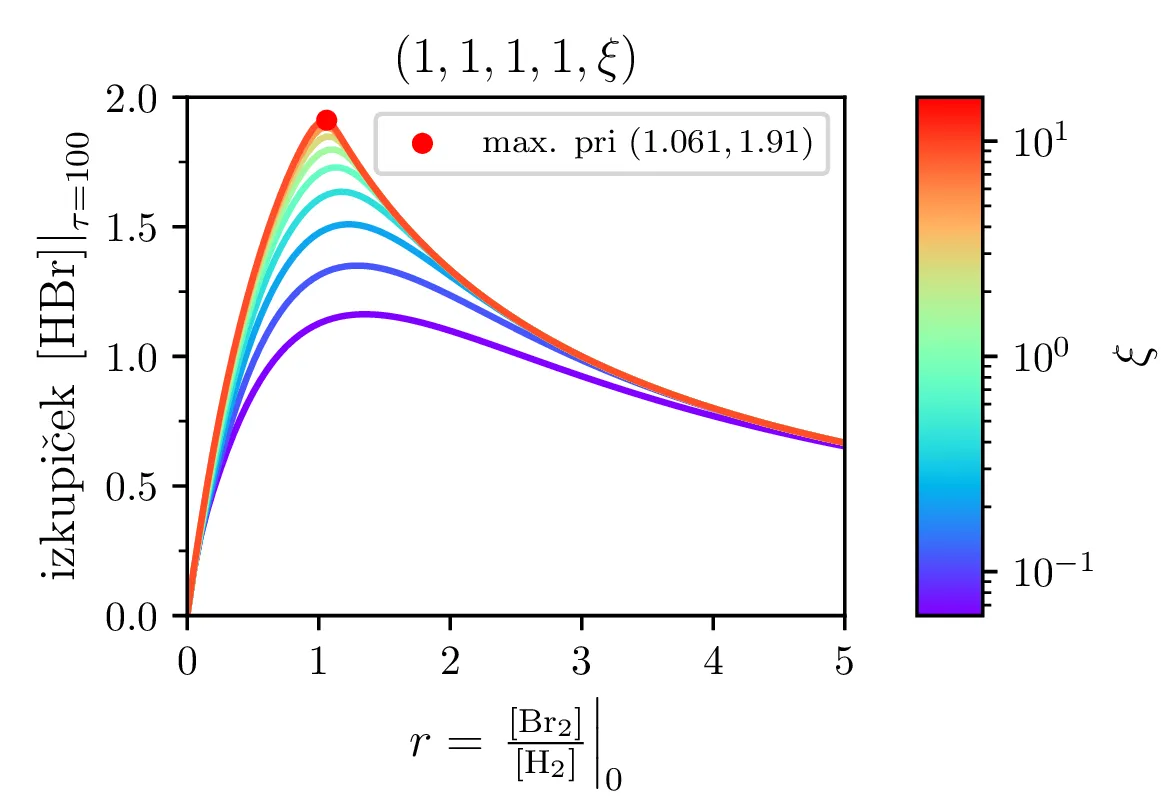
Z modelom sintezne reakcije lahko preučujemo precej pomembno lastnost, t. j. izkoristek ali izkupiček sinteze. Ker so naši začetni reaktanti molekulski \(\mathrm{Br}_2\) in \(\mathrm{H}_2\), sicer kot \[[\mathrm{Br}_2]_0 = 1, \quad [\mathrm{H}_2]_0 = 1,\] ali splošneje v nekem razmerju \[[\mathrm{Br}_2]_0 = \frac{2r}{r+1}, \quad [\mathrm{H}_2]_0 = \frac{2}{r+1},\] je povsem očitno, da smo navzgor omejeni kot \[\text{izkupiček: } [\mathrm{HBr}]_{\tau \to \infty} < 2.\] Kako blizu pa se lahko temu približamo, je odvisno od hitrostnih parametrov reakcij (2) in predvsem od začetnega razmerja molekulskih reaktantov \(r\), kot to vidimo na sliki 8 levo. Najboljši izkupiček reakcije, sicer okoli \(\sim 1.9\) je možno opaziti pri velikih \(\xi\) in za začetno razmerje reaktantov \(r \approx 1\).

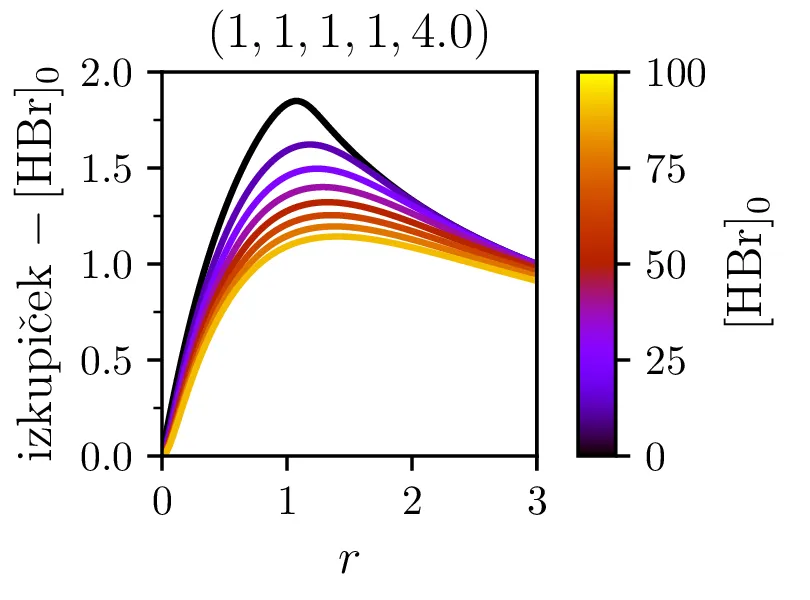
Dodajanje \(\mathrm{HBr}\) začetnim reaktantom ne pomaga pri izkupičku reakcije. Kot vidimo na sliki 8 desno, je izkupiček reakcije tedaj kvečjemu slabši. To je povsem smiselno, saj začetna koncentracija \(\mathrm{HBr}\) stalno razpada na \(\mathrm{Br}\) in \(\mathrm{H}_2\).

Več parametrov in boljši izkupiček

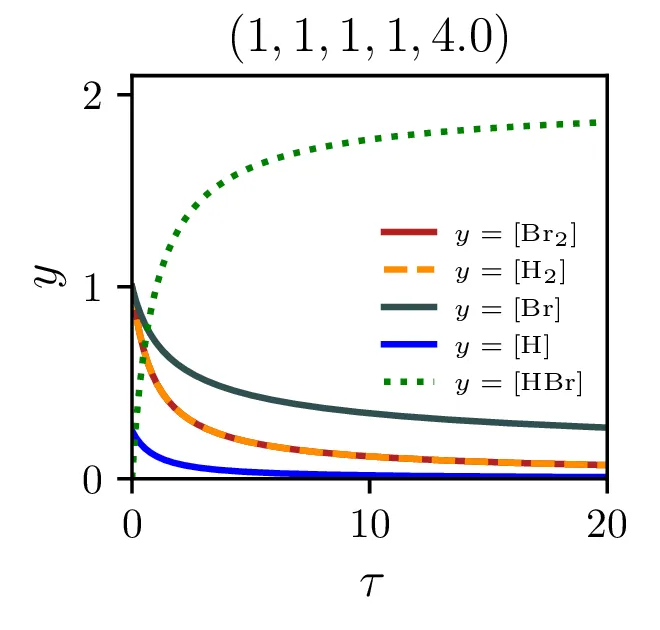
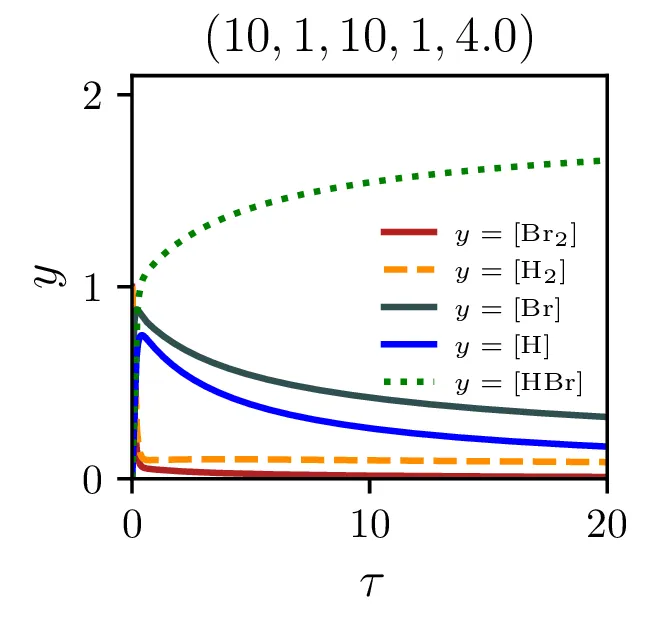
Naš proces sinteze (2) ima zares 5 prostih hitrostnih parametrov, \(\alpha, \alpha', \beta, \beta'\) in \(\xi\). Na sliki 9 vidimo, kako izgledajo poteki za različne hitrosti \(\xi\). Če primerjamo spodnje tri in zgornje tri slike vidimo tudi, kako je stacionarni približek mnogo slabši pri manjšem \(\xi\), kjer se vmesni produkti nabirajo v kaskadi dveh dvosmernih reakcij. To obnašanje za različne \(\xi\) se ujema tudi z odvisnostjo napake od \(\xi\) na sliki 7.

Izkupiček po dveh parametrih \(T, \xi\), ki določata hitrostne parametre \((\alpha, \alpha', \beta, \beta', \xi) = (T, 1, T, 1, \xi)\). Izkupiček za vsak \((T, \xi)\) izračunamo kot največji izkupiček med vsemi začetnimi razmerji reaktantov \(r \in [0, 5]\), t. j. kot \(\mathop{\mathrm{max}}_{r\in[0, 5]} \Big( \left. [\mathrm{HBr}] \right\vert_{\tau = 100} \Big)\). Za zadostno velike \(\xi\) vidimo plato pri precej širokem naboru \(T\), kjer je dosežen skoraj maksimalni možni izkoristek sinteze \(\sim2\).

Zaenkrat smo se omejili na primere, kjer prvi dve reakciji potekata enako hitro v obe smeri, spreminjali smo le hitrost enosmerne reakcije \(\xi\). Poglejmo še primer, kjer sta prvi dve reakciji nesimetrični in je \[\alpha > \alpha', \quad \beta > \beta'.\] Kot vidimo na sliki 11 je efekt to, da se skupaj z \(\mathrm{HBr}\) nasičita tudi koncentraciji \(\mathrm{Br}\) in \(\mathrm{H}\), ki so zdaj vsi efektivno končni produkti.

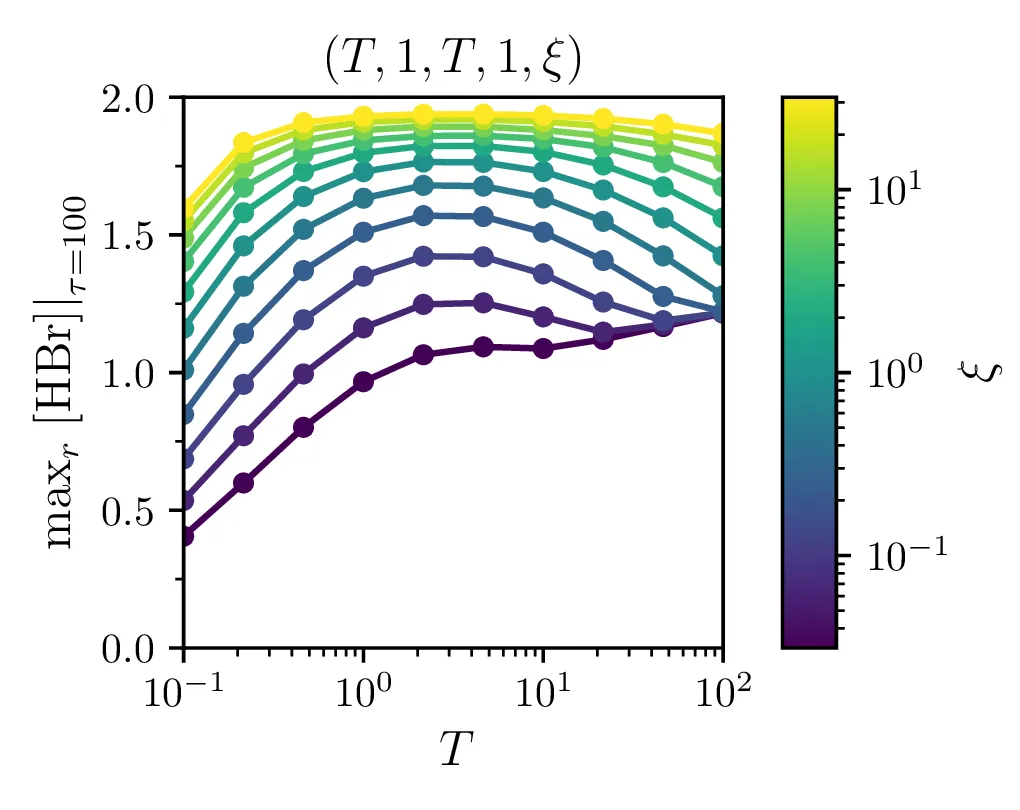
Z nekoliko več svobode v hitrostih parametrih bomo poskusili najti parametre za najboljši izkupiček sinteze. Sicer bomo parametre nastavili v obliki \[(\alpha, \alpha', \beta, \beta', \xi) = (T, 1, T, \xi),\] za zdaj dva prosta parametra \(T, \xi\). Izkupiček po teh dveh parametrih narišemo na sliki 10, kjer vidimo, da imamo kar nekaj svobode pri izbiri \(T\), saj ima oblika izkupička po temu parametru nekakšen plato blizu \(\sim 2\) za zadostno velike \(\xi\). Če bi bila zadnja reakcija počasnejša, t. j. bi bil \(\xi\) manjši, bi morali \(T\) izbrati bolj previdno.

Poteki za \(\tau \in [0, 20]\) in začetne pogoje \(([\mathrm{Br}_2], [\mathrm{H}_2], [\mathrm{Br}], [\mathrm{H}], [\mathrm{HBr}])_0 = (1, 1, 0, 0, 0)\). Parametri \(\alpha, \alpha', \beta, \beta'\) so \(10, 1, 10, 1\), v tem vrsten redu. Spreminjamo le hitrost \(\xi\). (Zgoraj od leve proti desni) Poteki, ki jih dobimo z integracijo sistema (10) za \(\xi \in \{ 4, 1/4, 1/100 \}\). (Zgoraj od leve proti desni) Poteki v stacionarnem približku (sistem (14) za \(\xi \in \{ 4, 1/4, 1/100 \}\).

Jodova ura

Ključne koncentracije v reakciji jodove ure (4), kjer predpostavimo, da je persulfata \(\mathrm{S_{2}O_{8}^{2-}}\) vedno v prebitku, so za dinamiko reakcije relevantne le koncentracije \([\mathrm{I^{-}}]\), \([\mathrm{I_2}]\) in \([\mathrm{S_{2}O_{3}^{2-}}]\). Za njih lahko direktno zapišemo sistem diferencialnih enačb

Poteki jodove ure za različne \(\lambda = \frac{\delta'}{\delta}\). (Levo) \(\lambda = 1\). (Sredinsko) \(\lambda = 10\). (Desno) \(\lambda = 100\).

\begin{equation}\begin{aligned} \mathop{[\mathrm{I^{-}}]}^\bullet = -2\Big( \delta[\mathrm{I^{-}}] - \delta'[\mathrm{S_{2}O_{3}^{2-}}][\mathrm{I_2}]& \Big), \nonumber \\ \mathop{[\mathrm{I_2}]}^\bullet = \delta[\mathrm{I^{-}}] - \delta'[\mathrm{S_{2}O_{3}^{2-}}][\mathrm{I_2}]&, \nonumber \\ \mathop{[\mathrm{S_{2}O_{3}^{2-}}]}^\bullet = -\delta'[\mathrm{S_{2}O_{3}^{2-}}][\mathrm{I_2}]&. \label{eq:clock-system} \end{aligned}\end{equation}

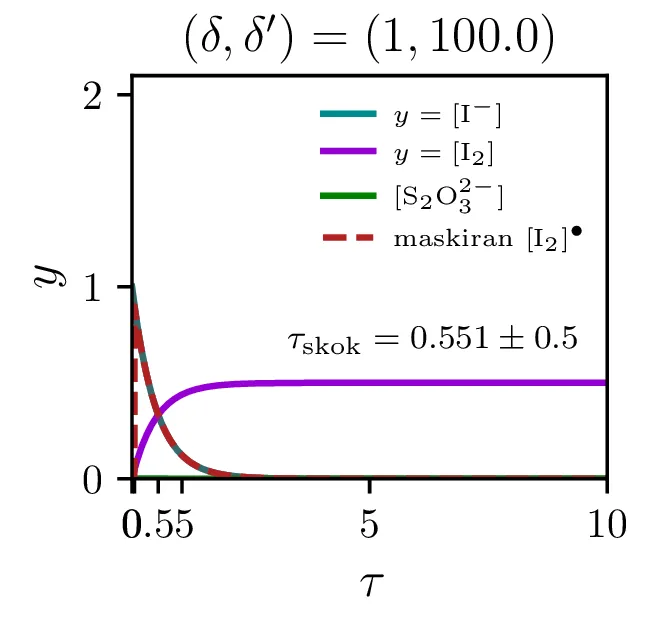
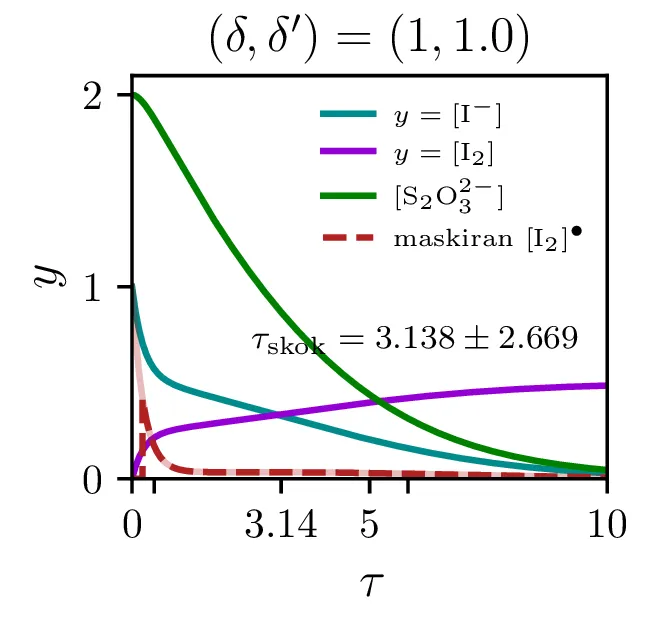
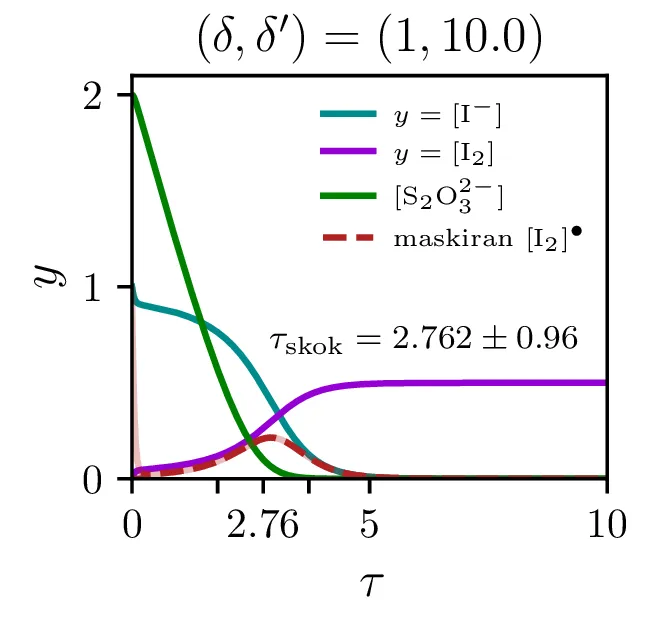
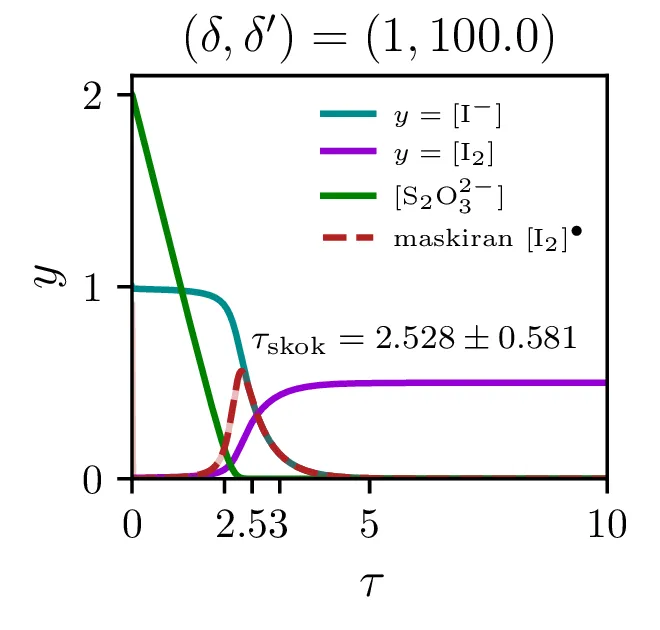
Na sliki 12 vidimo poteke reakcije za \(\lambda = \frac{\delta'}{\delta} \in \{ 1, 10, 100 \}\). Vidimo lahko, da se prehod zgodi, ko koncentracija \(\mathrm{S_{2}O_{3}^{2-}}\) pade dovolj nizko. Prehod je ostrejši za večje razmerje \(\lambda\), pri zelo majhnih razmerjih \(\sim 1\) je tudi njegova oblika nekoliko drugačna, ni več sigmoida, temveč jo sestavlja začeten skok, nato pa postopno naraščanje.

Čas in ostrina prehoda

Čas trajanja ure in resolucijo ure, ki jo določa ostrina tega prehoda, bomo karaketrizirali z dvemi števili. Ko je potek \([\mathrm{I_2}]\) sigmoidne oblike, je njegov odvod funkcija z jasnim vrhom pri prehodu. Ko sistem (4) rešujemo na intervalu od \(a\) do \(b\), lahko čas skoka (če interval skok vsebuje) najdemo kot \[\tau_\mathrm{skok} \vcentcolon=\frac{\int_a^b \tau \mathop{[\mathrm{I_2}]}^\bullet \,\mathrm{d}\tau}{\int_a^b \mathop{[\mathrm{I_2}]}^\bullet \,\mathrm{d}\tau}.\] Kot smo karaketrizirali čas skoka, lahko naredimo še za širino prehoda ob tem času, ki karakterizira relolucijo ure, sicer kot \[\sigma_{\tau,\mathrm{skok}} \vcentcolon=\sqrt{\frac{\int_a^b (\tau - \tau_\mathrm{skok})^2 \mathop{[\mathrm{I_2}]}^\bullet \,\mathrm{d}\tau}{\int_a^b \mathop{[\mathrm{I_2}]}^\bullet \,\mathrm{d}\tau}}.\] Števili \(\tau_\mathrm{skok}\) in \(\sigma_{\tau,\mathrm{skok}}\) sta povprečje in širina normaliziranega odvoda \([\mathrm{I_2}]\). Na sliki 12 vidimo take krivulje v rdečem, na osi in s tekstom pa sta označena tudi \(\tau_\mathrm{skok}\) in \(\sigma_{\tau,\mathrm{skok}}\) za tako rdečo krivuljo.

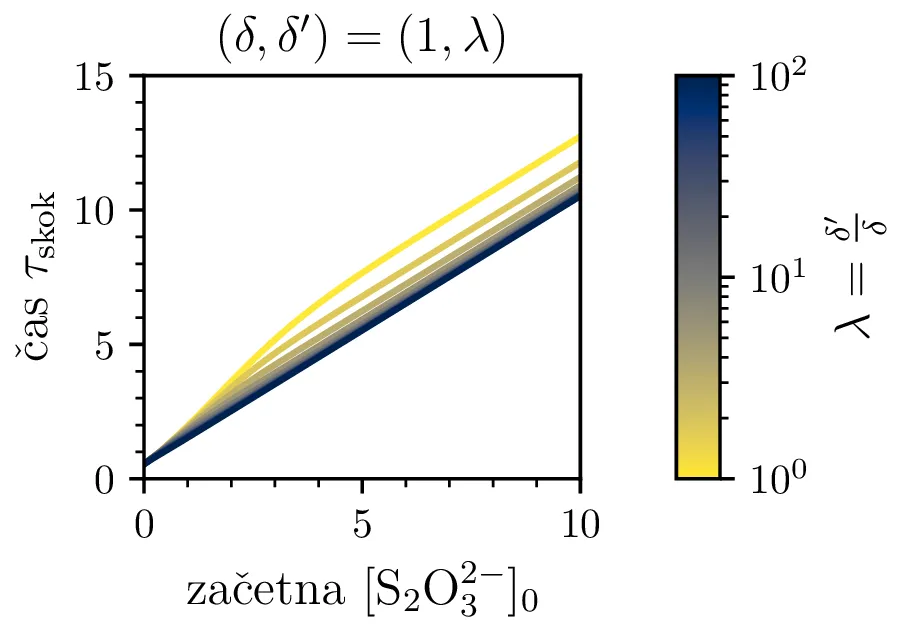
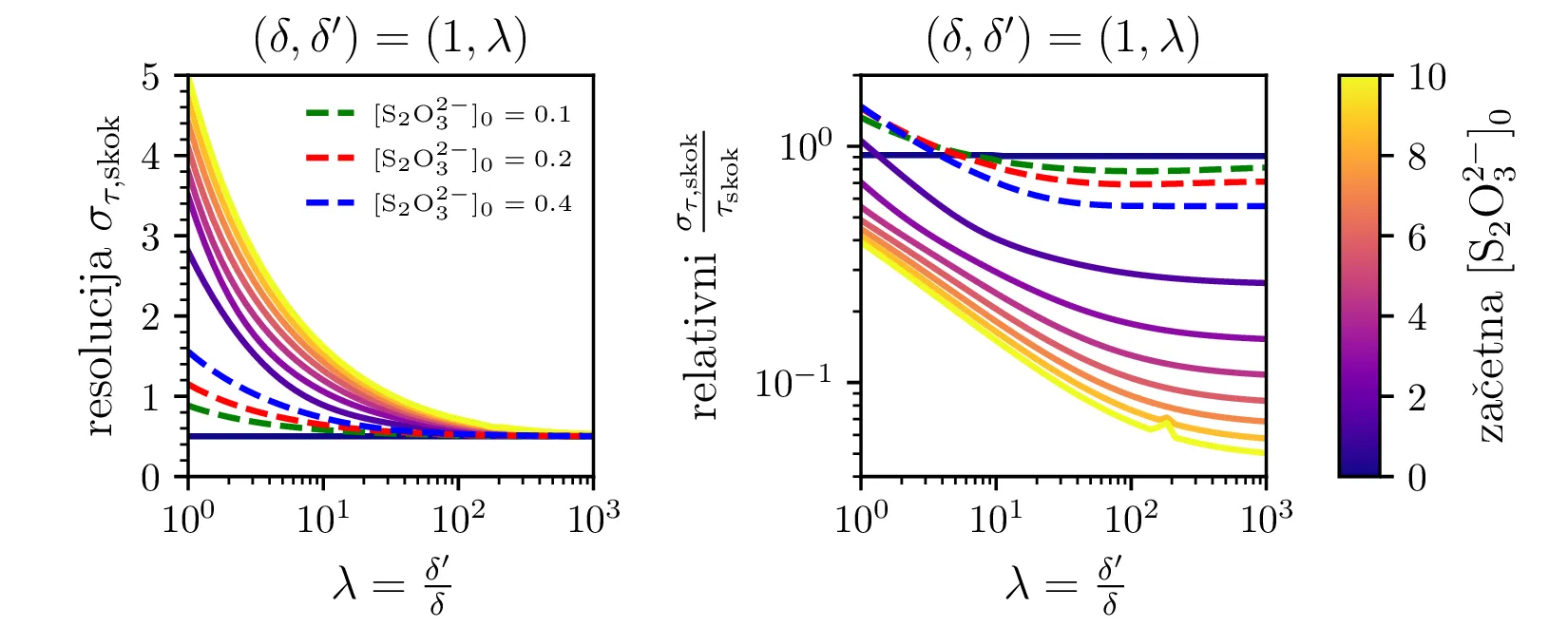
Na sliki 13 je narisan čas \(\tau_\mathrm{skok}\) v odvisnosti od začetne koncentracije \(\mathrm{S_{2}O_{3}^{2-}}\). Ker se \(\mathrm{S_{2}O_{3}^{2-}}\) porablja enakomerno, je čas trajanja ure pri velikih \(\lambda\) zelo lepo linearno sorazmeren začetni koncentraciji \(\mathrm{S_{2}O_{3}^{2-}}\). Sama resolucija ure, torej \(\sigma_{\tau,\mathrm{skok}}\) je zelo odvisna od razmerja hitrosti reakcij v (4). Kot vidimo na sliki 14, je \(\sigma_{\tau,\mathrm{skok}}/ \tau_\mathrm{skok}\) za razmerje \(\lambda \approx 100\) lahko manjši od \(< 1/10\). Za večje \(\lambda\) bi lahko bila resolucija še boljša, a sistem je potem bolj zahteven za integracijo, saj so prehodi res ostri in to povzroča težave pri numerični integraciji. Z RK45 metodo je za \(\lambda = 1000\) potrebno okoli \(500k\) točk. Verjetno bi kakšen drug integrator tu bil bolj optimalen.

(Levo) Čas trajanja jodove ure \(\tau_\mathrm{skok}\) v odvisnosti od začetne koncentracije \(\mathrm{S_{2}O_{3}^{2-}}\), narisan za različne \(\lambda = \frac{\delta'}{\delta}\). Za velike \(\lambda\) je razmerje zelo lepo linearno. (Desno) Primer poteka z zelo majhno začetno koncentracijo \(\mathrm{S_{2}O_{3}^{2-}}\). Vidimo, da prehod začne kar ob času \(\tau = 0\). Zaradi načina, na katerega smo definirali \(\tau_\mathrm{skok}\), je še vedno \(> 0\), kar bi se morda dalo rešiti z integracijo tudi v \(-\mathrm{d}\tau\).

Resolucija jodove ure \(\sigma_{\tau,\mathrm{skok}}\) v odvisnosti od \(\lambda = \frac{\delta'}{\delta}\), narisan za različne začetne koncentracije \(\mathrm{S_{2}O_{3}^{2-}}\). (Levo) Absolutna resolucija. (Desno) Relativna resolucija. Majhen skokec med \(10^2\) in \(10^3\) je napaka numerične integracije.

Viri

[1]

J. H. Hubbard in B. H. West, Differential Equations: A Dynamical Systems Approach: Ordinary Differential Equations. New York: Springer, 1991.

[2]

S. P. N. Ernst Hairer Gerhard Wanner, Solving Ordinary Differential Equations: Nonstiff Problems, 2. izd., let. 2. v Springer Series in Computational Mathematics 8, vol. 2. Springer-Verlag Berlin Heidelberg, 1993.

Modelska analiza I 5. naloga: Modeli kemijskih reakcij