Populacijski modeli
SIR model epidemije, populacijski model Lotka-Volterra in model optičnega črpanje v laserju
Navodila
-
Razišči preprost SIR model epidemije. V modelu populacijo razdelimo v tri razrede: (D) zdravi in dovzetni, (B) bolni in kliconosni, (I) imuni: nedovzetni in nekliconosni. Bolezen se širi s stiki med zdravimi in bolnimi. Bolnik preide s konstantno verjetnostjo med imune (ozdravi ali umre).
Preuči standardni standardni deterministični model zajci-lisice (model Lotka-Volterra).
Analiziraj fazni portret za populacijski model laserja s konstantnim črpanjem.
Model epidemije
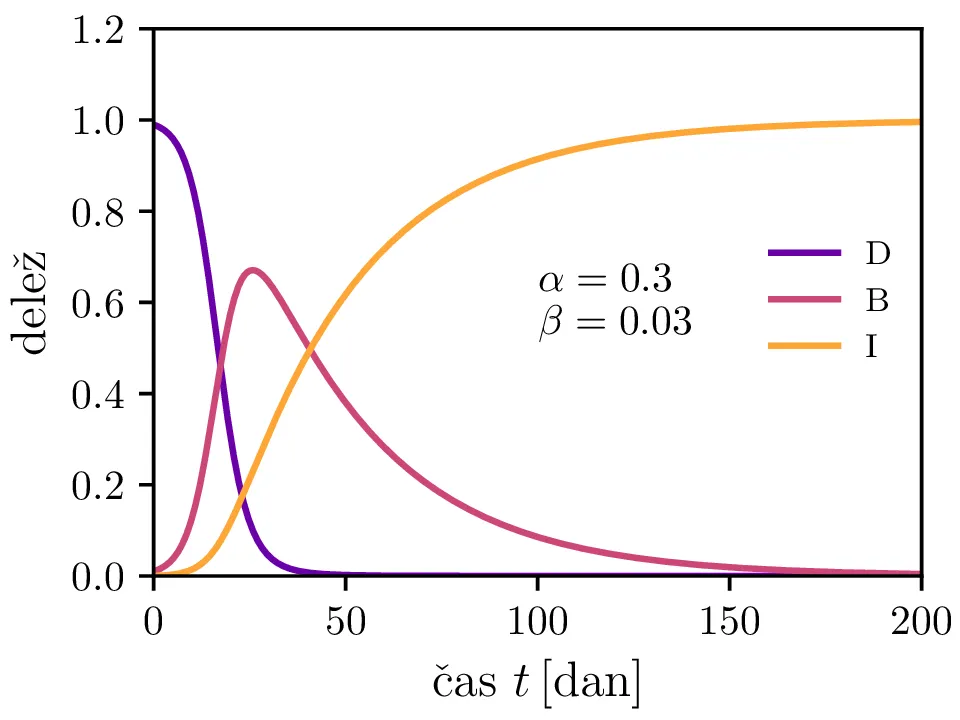
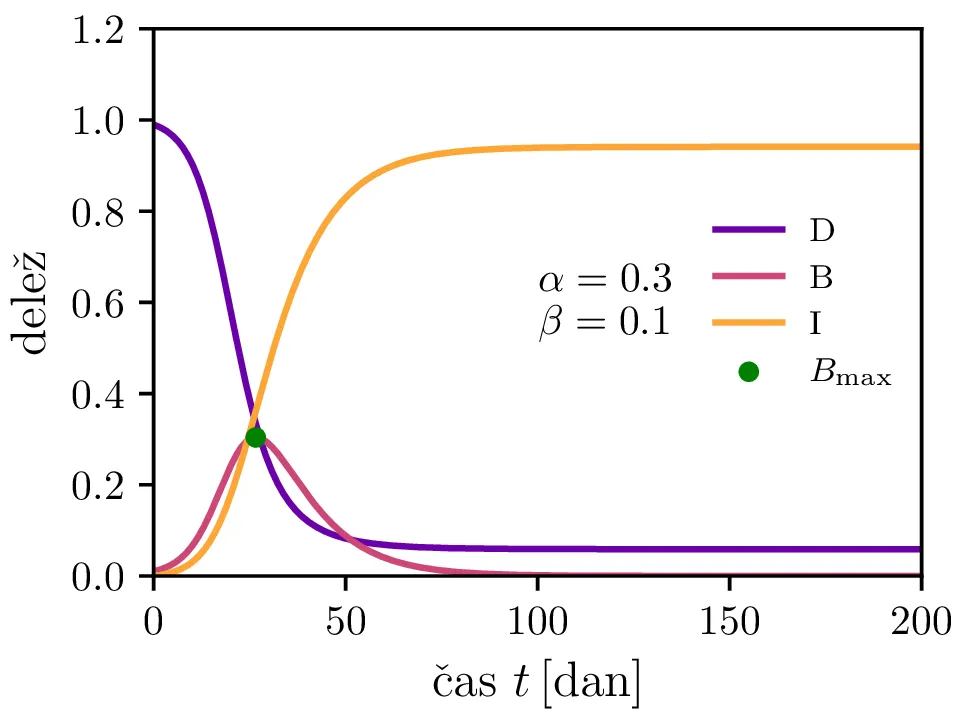
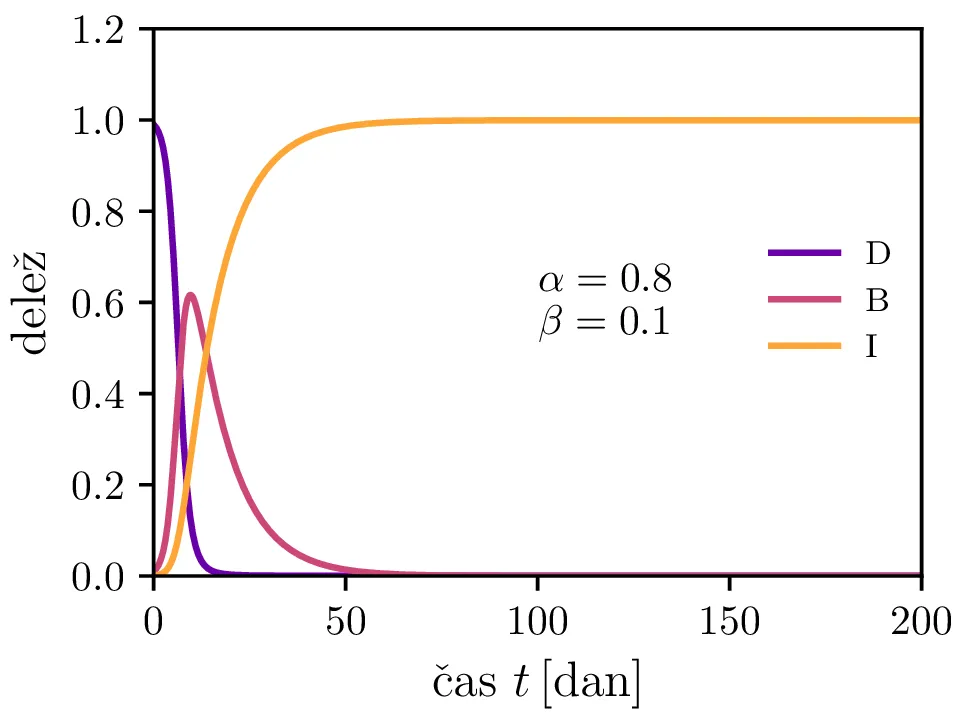
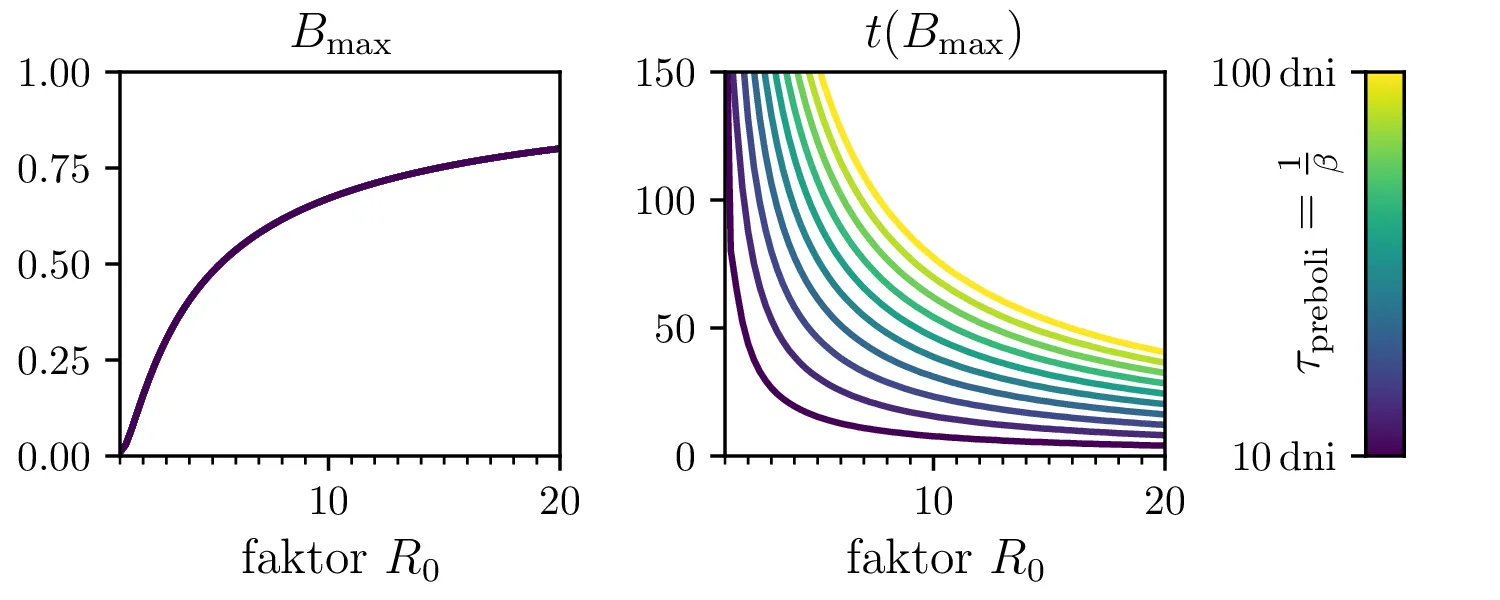
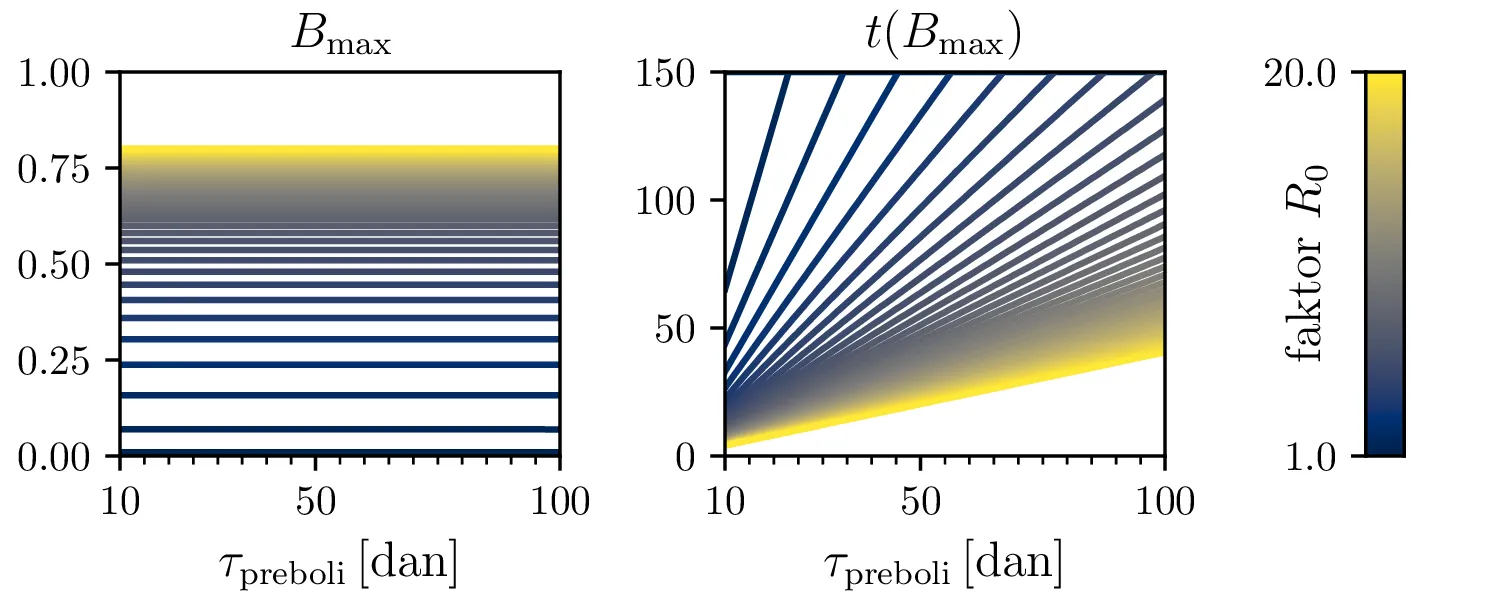
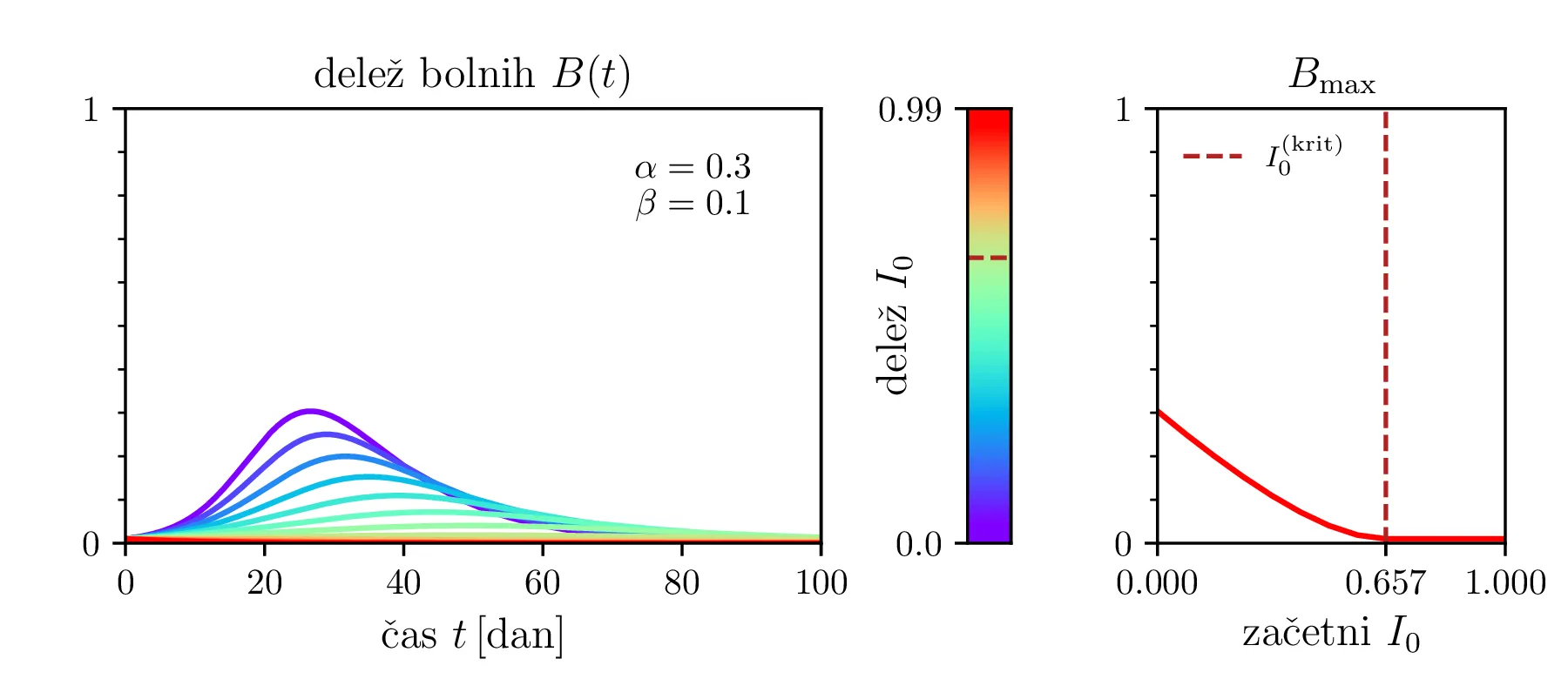
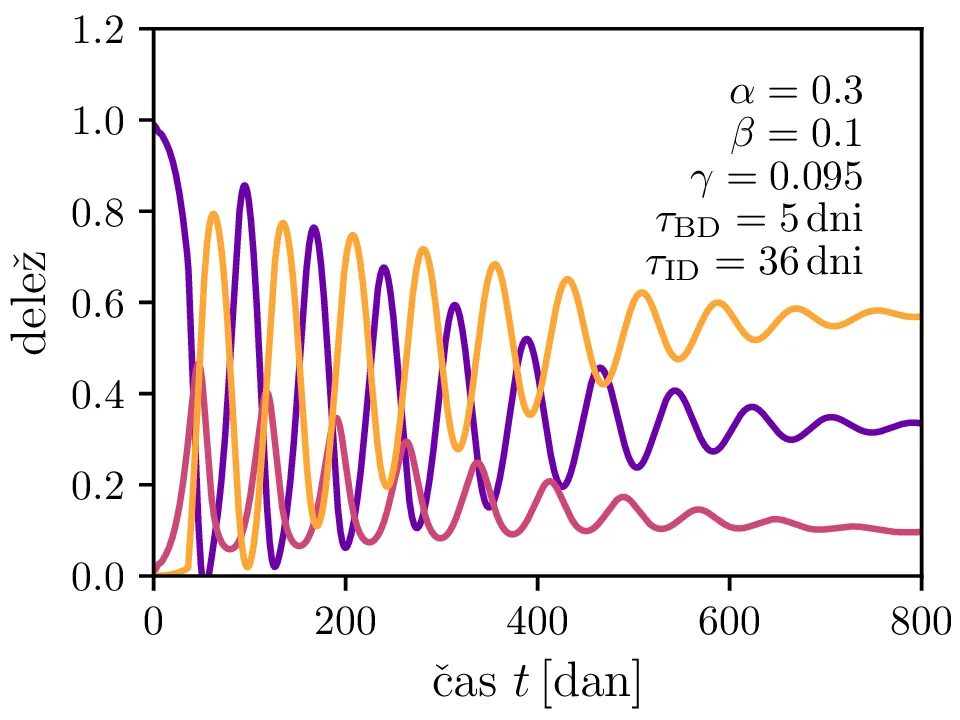
Preprost model epidemije modeliramo kot sistem navadnih diferencialnih enačb \begin{equation}\begin{aligned} \dot{D} &= -\alpha DB, \nonumber \\ \dot{B} &= \alpha DB - \beta B, \label{eq:SIR} \\ \dot{I} &= \beta B. \nonumber \end{aligned}\end{equation} Faktor \(\alpha\) je pri tem t. i. reproduktivni faktor bolezni, ki narekuje hitrost njenega širjenja. Takoj v prvi enačbi v sistemu vidimo, da se bo število dovzetnih le zmanjševalo \[D(t) \le D_0,\] posledično pa to, ali se bo epidemija sploh širila, narekuje pogoj \begin{equation}\dot{B} \le I(\alpha D_0 - \beta). \label{eq:ineq}\end{equation} Če želimo, da se bolezen vsaj na neki točki širi (da je \(\dot{B} > 0\)), mora biti desna stran neenakosti (2) pozitivna, torej mora veljati \begin{equation}R :=\frac{\alpha D_0}{\beta} > 1, \label{eq:R}\end{equation} pri čemer smo uvedli t. i. reproduktivni faktor \(R\). Če je na začetku dovzetna vsa populacija, je to t. i. osnovni reproduktivni faktor. \[R_0 :=R\vert_{D_0 = 1} = \frac{\alpha}{\beta}\] Ta parameter je široko uporabljen v imunološki literaturi in tudi poročan tekom bolezni kot je bil npr. Covid-19 (glej tabelo 1). Za neke smiselne začetne parametre bomo predpostavili, da tipično ljudje bolezen prebolijo (ali pa umrejo) v času 10-ih dni \[\beta = \frac{1}{\tau_\text{preboli}} \approx \frac{1}{10\,\text{dni}} = 0.1.\] Če torej vzamemo nek smiseln \(R_0 \approx 3\) za SARS-CoV, lahko izberemo za \(\alpha \approx 0.3\). Narišemo primere poteke epidemije za različne \(\alpha, \beta\) (glej sliko 1). Kako točno je vrh \(B_\text{max}\) in čas njegovega nastopa odvisen od parametrov epidemije, lahko vidimo na sliki 2, kjer namesto parametrov \(\alpha, \beta\) uporabimo ekvivalentna \(R_0, \tau_\text{preboli}\). Vidimo, da večji \(\alpha\) epidemijo ojača (večji \(B_\text{max}\)) in pospeši (manjši \(t(B_\text{max})\)), medtem pa manjši \(\beta\) epidemijo zgolj ojača (večji \(B_\text{max}\)), časa njenega vrha pa ne spremeni.
| \(\mathbf{R}_0\) | |
|---|---|
| Wuhan | 2.4-2.6 |
| EU | 3 |
| \(\alpha\) | 4-5 |
| \(\delta\) | 5-8 |
| ošpice | 12-18 |
Odvisnost vrha epidemije
Zanima nas tudi, koliko je maksimalno število bolnih \(B_\mathrm{max}\) in kdaj tak vrh epidemije nastopi, t. j. čas \(t(B_\mathrm{max})\). To odvisnost narišemo na sliki 2 po parametrih \((R_0, \tau_\text{preboli})\) (namesto \((\alpha, \beta)\)).
Mutacija virusa in cepljenje
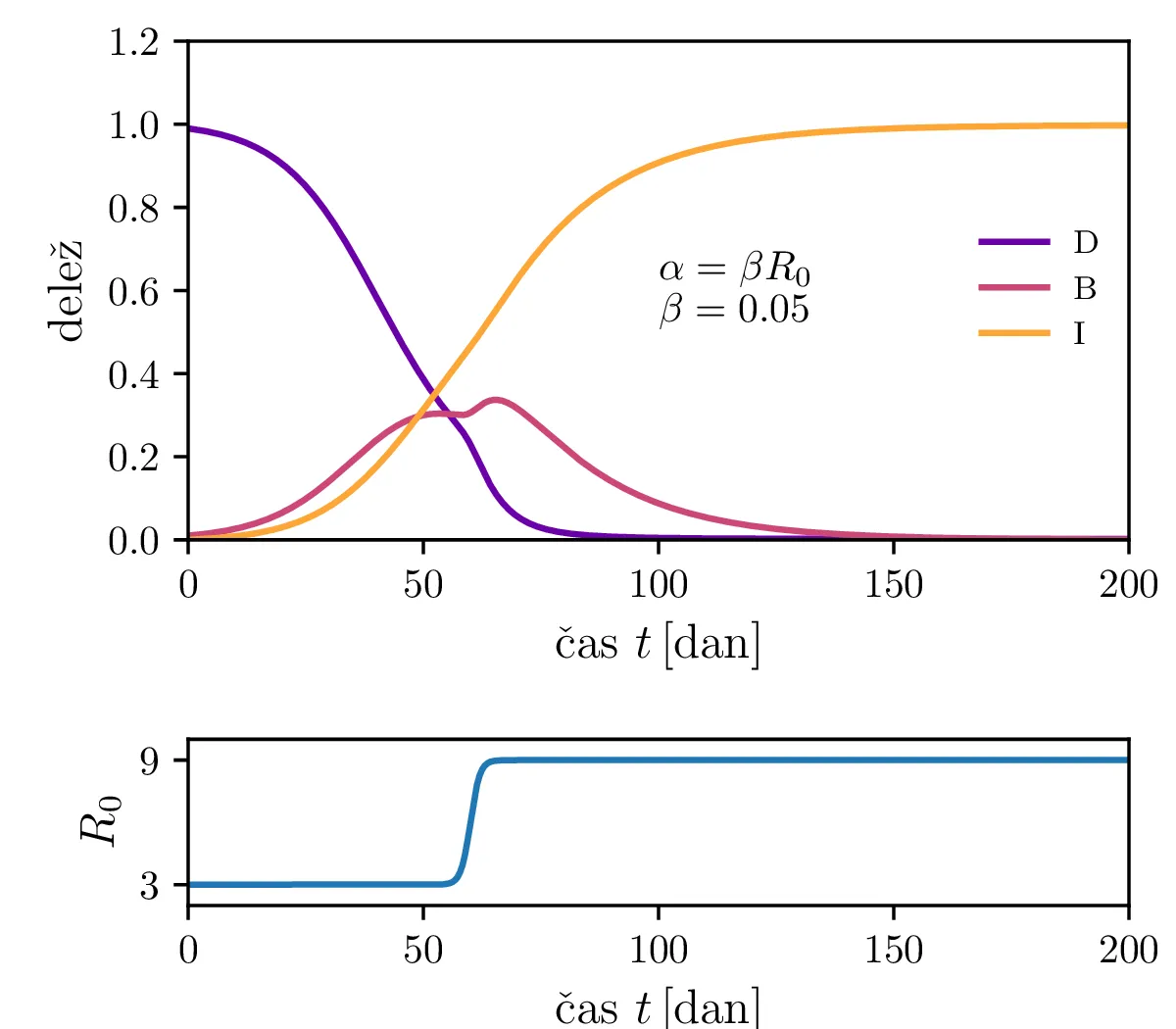
Če virus med potekom epidemije mutira, se mu lahko spremeni npr. reproduktivni faktor (glej tabelo 1). To lahko povzroči sekundarni vrh epidemije, ki je višji od začetno pričakovanega (slika 3).
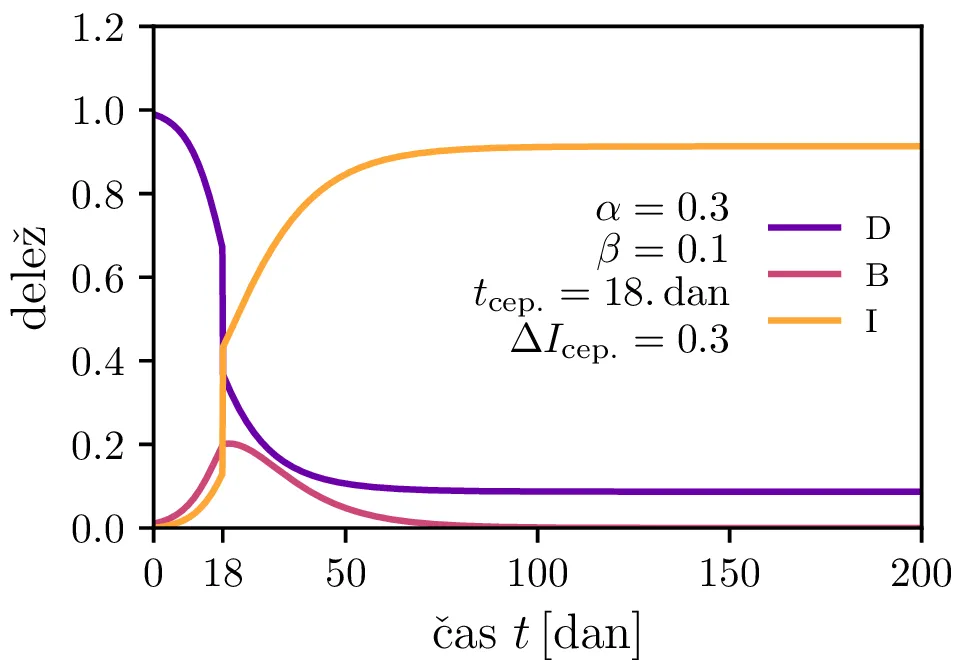
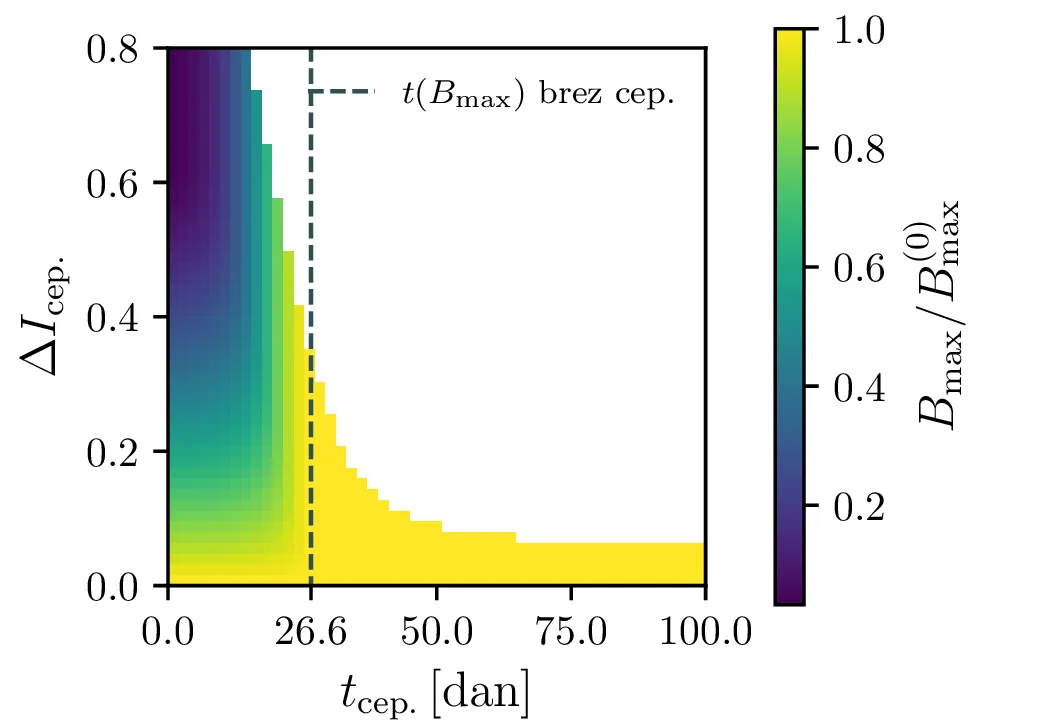
V model bomo poskusili vključiti tudi pojav cepljenja. V nekem trenutku \(\tau_\text{cep.}\) bomo precepili \(\Delta I_\text{cep.}\) delež populacije (slika 5 zgoraj). Kako čas cepljenja in delež cepljenja vpliva na vrh epidemije vidimo na sliki 5 spodaj.
Inkubacijska doba in popuščanje imunosti
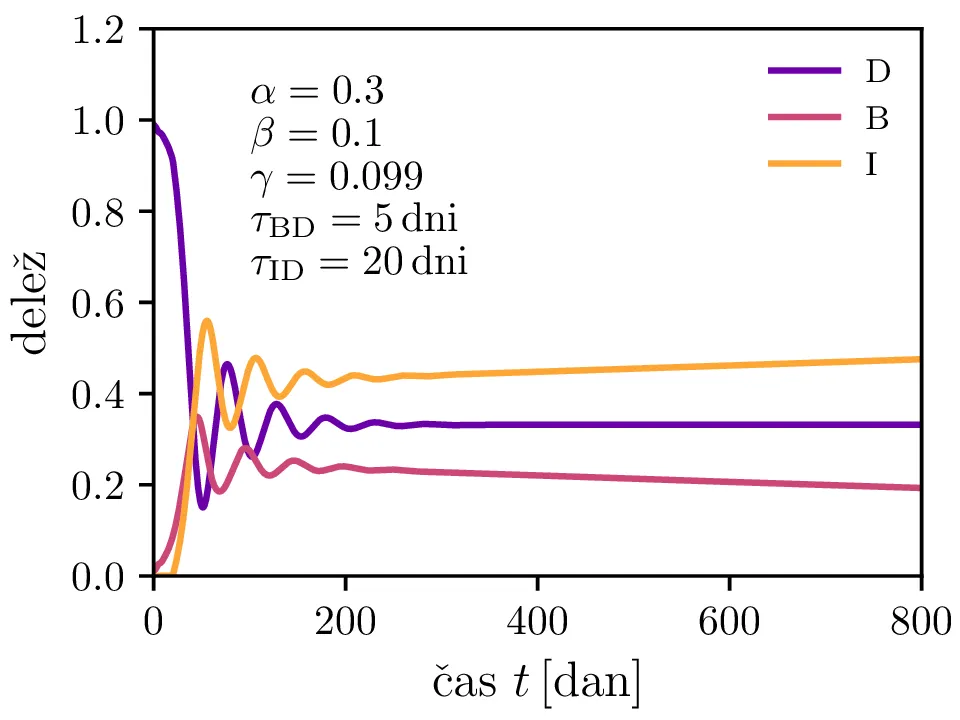
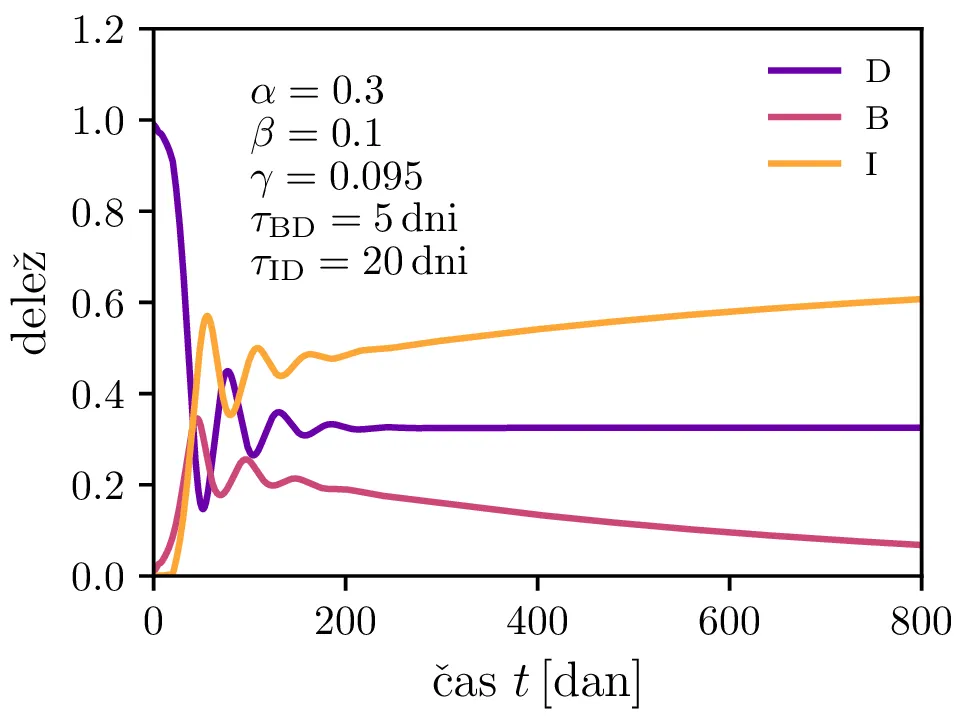
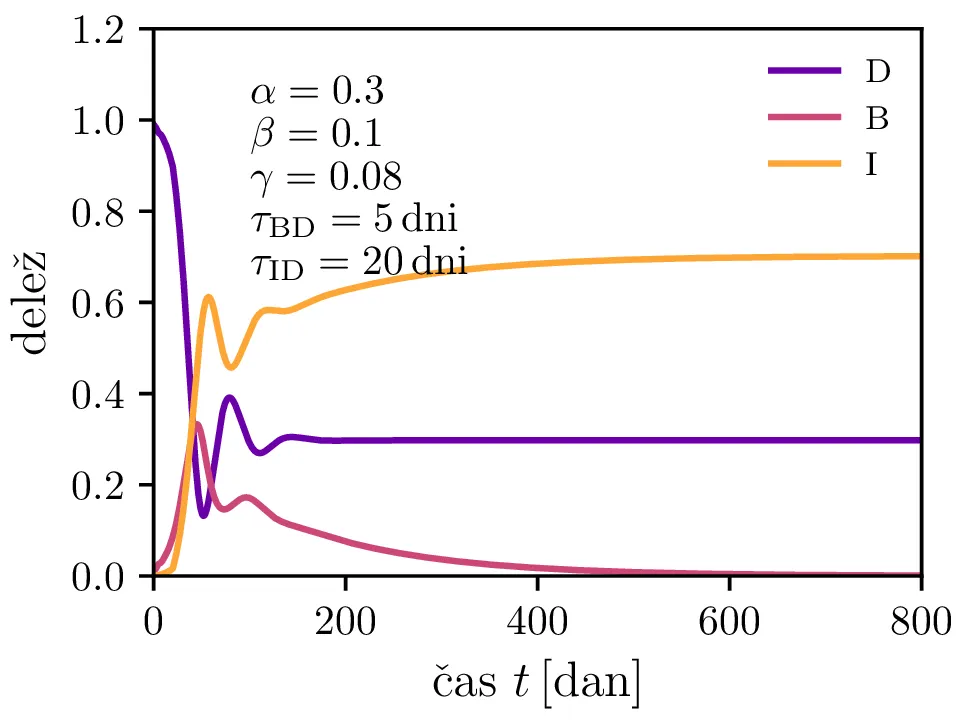
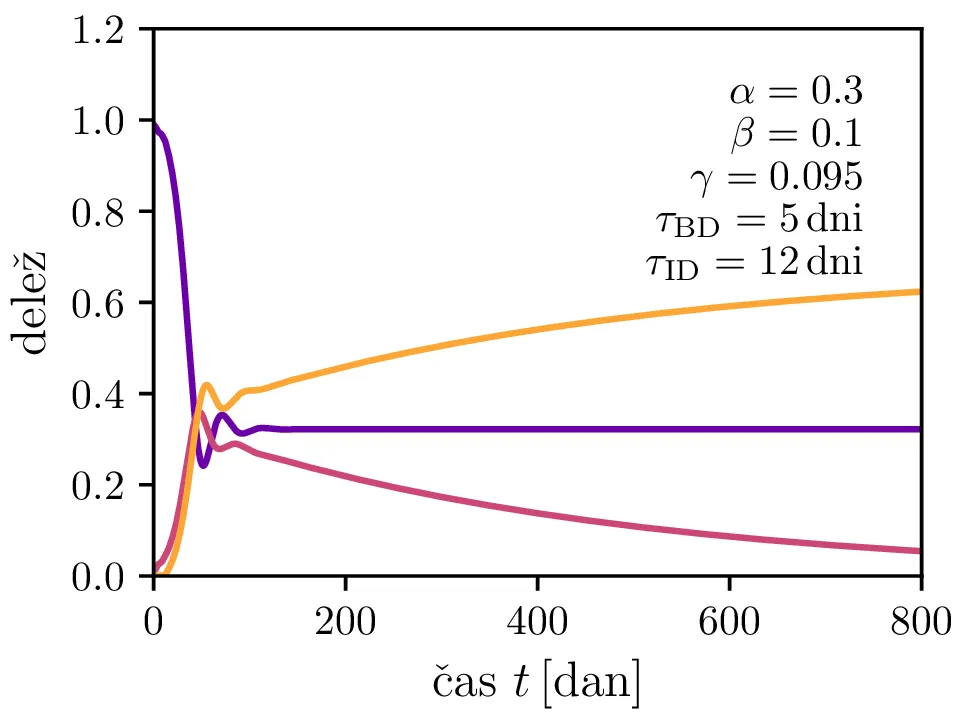
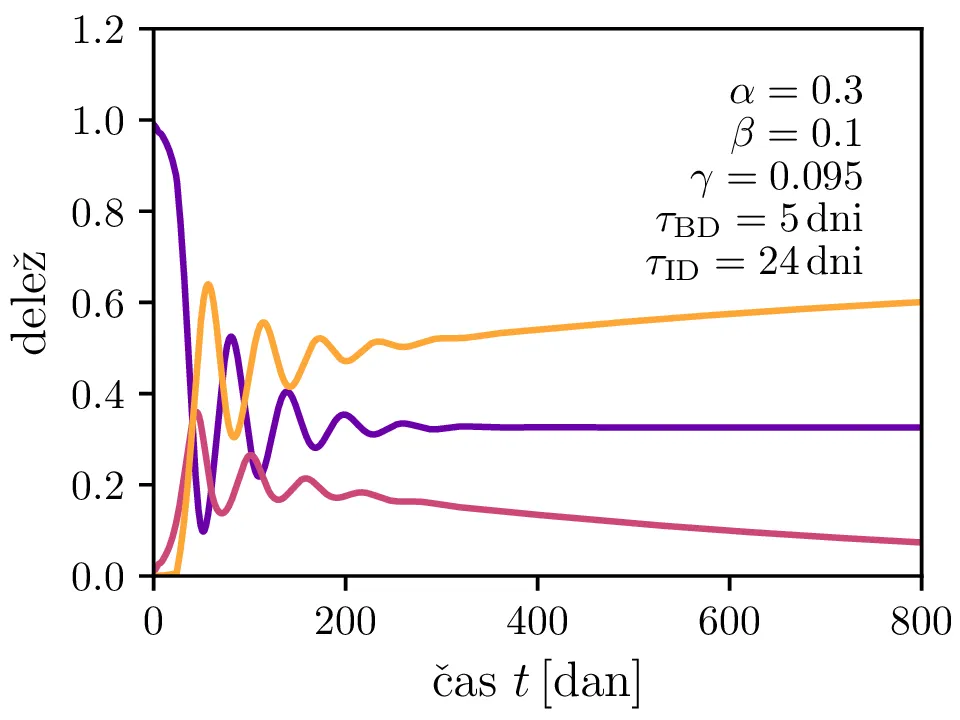
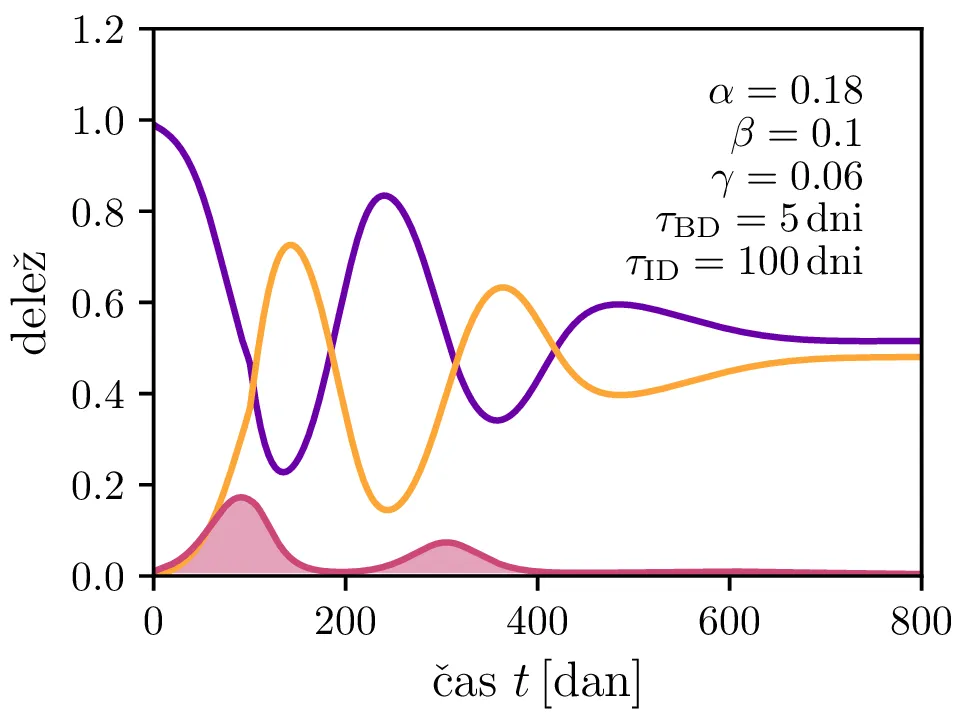
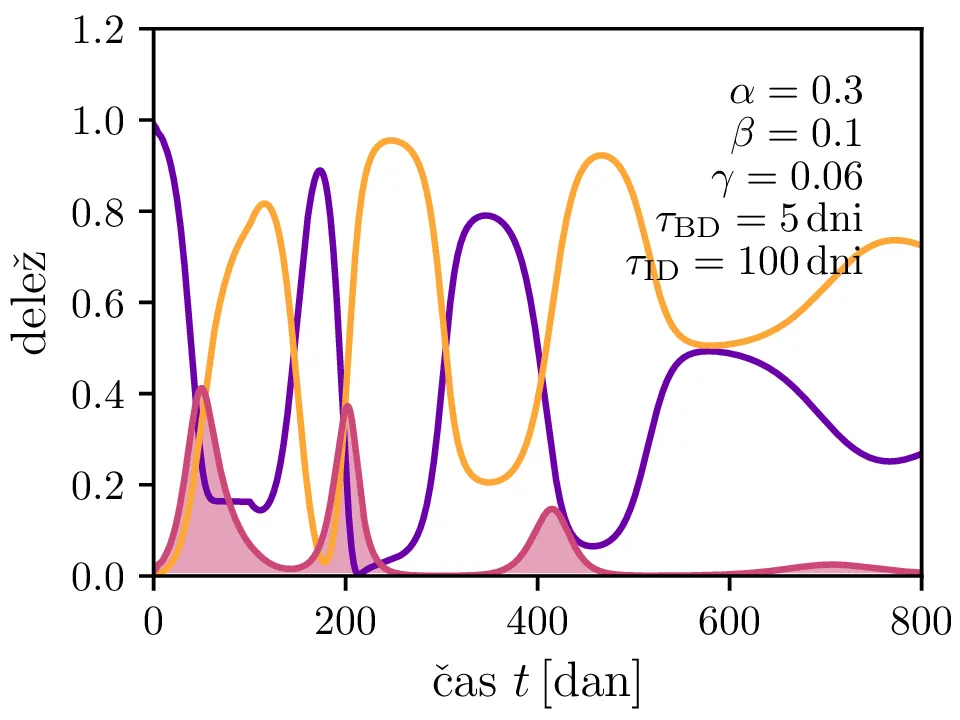
Po vzoru [2] dodamo našemu modelu (1) še inkubacijsko dobo \(\tau_\text{DB}\) in pa člen \(\gamma I_{(t - \tau_\text{ID})}\), ki opisuje popuščanje imunosti z specifično verjetnostjo \(\gamma\) po času \(\tau_\text{ID}\). Po novem se sistem diferencialnih enačb glasi \begin{equation}\begin{aligned} \dot{D} &= -\alpha D_{(t - \tau_\text{DB})} B_{(t - \tau_\text{DB})} + \gamma I_{(t - \tau_\text{ID})}, \nonumber \\ \dot{B} &= \alpha D_{(t - \tau_\text{DB})} B_{(t - \tau_\text{DB})} - B_{(t - \tau_\text{BI})}, \label{eq:dde} \\ \dot{I} &= B_{(t - \tau_\text{BI})} - \gamma I_{(t - \tau_\text{ID})}. \nonumber \end{aligned}\end{equation} Rešitve takšnega sistema nam zdaj ponudijo novo oscilatorno dinamiko (slike 6, 7 in 8). Ob pravi izbiri parametrov
Zajci in lisice
Zdaj si bomo pogledali še populacijski model Lotka-Volterra, ki opisuje dinamiko plena (zajci \(Z\)) in plenilcev (lisice \(L\)) \begin{equation}\begin{aligned} \dot{Z} &= \alpha Z - \beta ZL, \nonumber \\ \dot{L} &= -\gamma L + \delta ZL. \label{eq:LV} \end{aligned}\end{equation} Uvedli bomo brezdimenzijske količine \[\mathcal{Z}= \frac{Z}{Z_0}, \quad \mathcal{L}= \frac{L}{L_0}, \quad \tau = \frac{t}{t_0},\] pri čemer sta \(Z_0, L_0\) t. i. ravnovesni populaciji plena \begin{equation}Z_0 = \frac{\delta}{\gamma}, \qquad L_0 = \frac{\alpha}{\beta}. \label{eq:units}\end{equation} Če ju vstavimo v (5), ne bo nobene dinamike, sistem bo preprosto ostal v tem stanju s konstantnima populacijama zajcev in lisic. V količinah \((\mathcal{Z}, \mathcal{L}, \tau)\) dobimo nov zapis Lotka-Volterra sistema \[\begin{aligned} \dot{\mathcal{Z}} &= \alpha t_0 \left( \mathcal{Z}- \mathcal{Z}\mathcal{L}\right), \\ \dot{\mathcal{L}} &= \gamma t_0 \left( \mathcal{Z}\mathcal{L}- \mathcal{L}\right). \end{aligned}\] Tedaj lahko vpeljemo brezdimenzijski parameter \(r\) in karakteristični čas \begin{equation}r :=\sqrt{\frac{\alpha}{\gamma}}, \qquad t_0 = \frac{1}{\sqrt{\alpha \gamma}}. \label{eq:r}\end{equation}
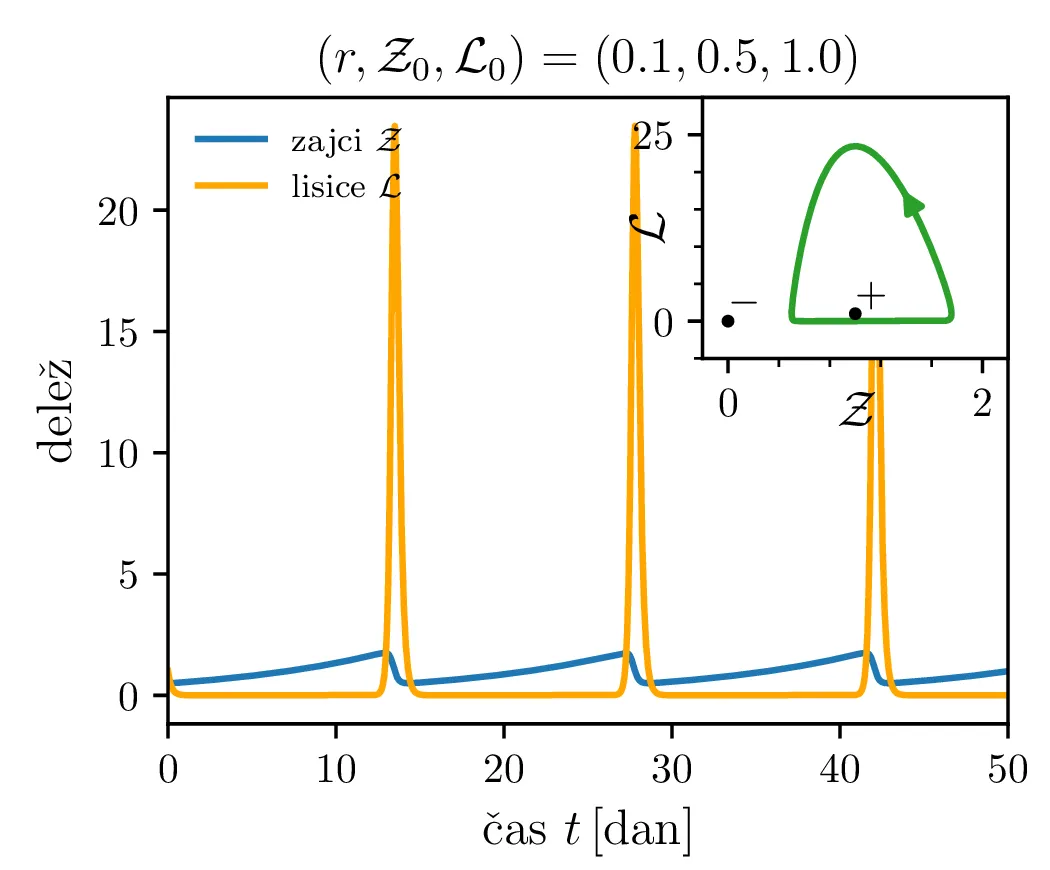
Parameter \(r\) označuje razmerje med plodnostjo plena in uspešnostjo plenilcev. Majhen \(r\) označuje plen, ki se množi relativno počasi, in plenilce, ki so izjemno uspešni v lovi na njih. Lotka-Volterra enačbi pa zdaj zavzameta obliko \begin{equation}\begin{aligned} \dot{\mathcal{Z}} &= r \left( \mathcal{Z}- \mathcal{Z}\mathcal{L}\right), \nonumber \\ \dot{\mathcal{L}} &= r^{-1} \left( \mathcal{Z}\mathcal{L}- \mathcal{L}\right). \label{eq:LV-nondim} \end{aligned}\end{equation} Za ta sistem lahko zapišemo Jakobian (linearizacijo sistema) za Lotka-Volterra sistem (8) \[J(r, \mathcal{Z}, \mathcal{L}) = \begin{bmatrix} r(1 - \mathcal{L}) & -r\mathcal{Z}\\ r^{-1}\mathcal{L}& r^{-1}(\mathcal{Z}- 1) \end{bmatrix}.\] V stacionarni točki \((\mathcal{Z}, \mathcal{L}) = (0, 0)\) je ta Jakobian \[J(r, 0, 0) = \begin{bmatrix} r & 0 \\ 0 & -r^{-1} \end{bmatrix}.\] Vidimo, da sta lastni vrednosti \(r\) in \(-r^{-1}\) vedno nasprotnih predznakov, torej imamo v tej točki sedlo. Še posebej za majhne \(r\) je ob bližanju \((0, 0)\) značilna dinamika skorajšnjega izumrtja, kjer plenilci praktično iztrebijo plen in od stradanja tudi sami skoraj sami izumrejo (prva slika 9), nato pa sledi dolga faza počasne obnove zaloge plena. V faznem diagramu se vedno bolj bližamo t. i. točki izumrtja \[\text{izumrtje: } T^{-} = (0, 0).\]
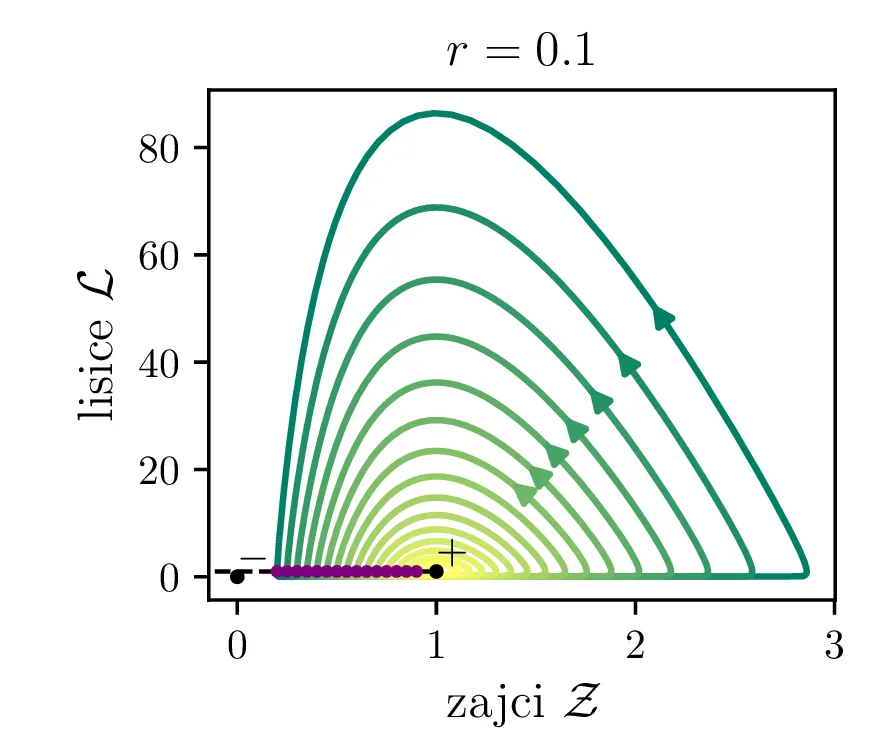
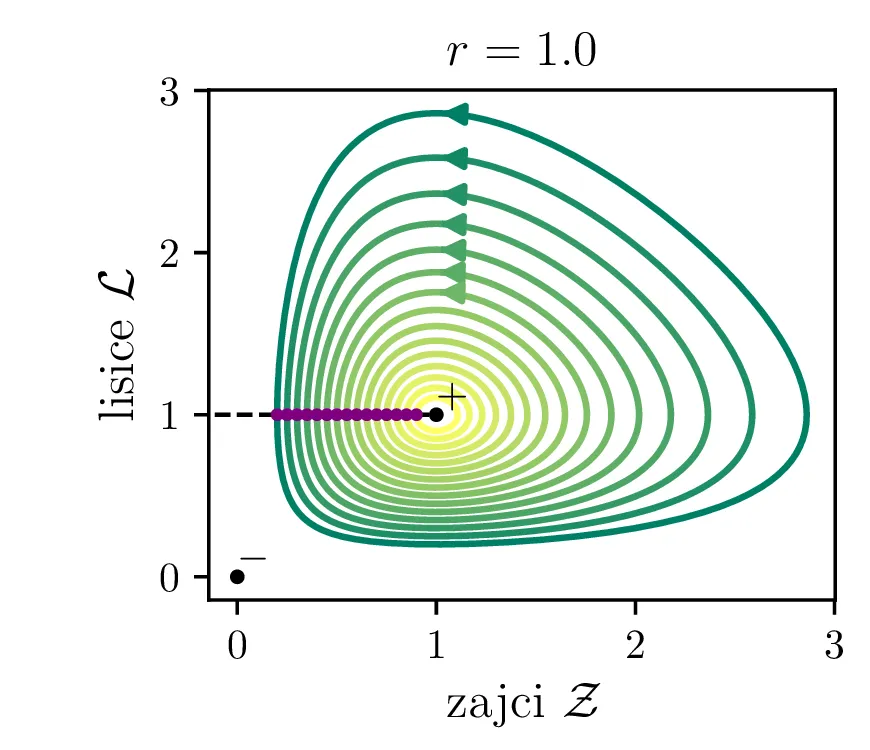
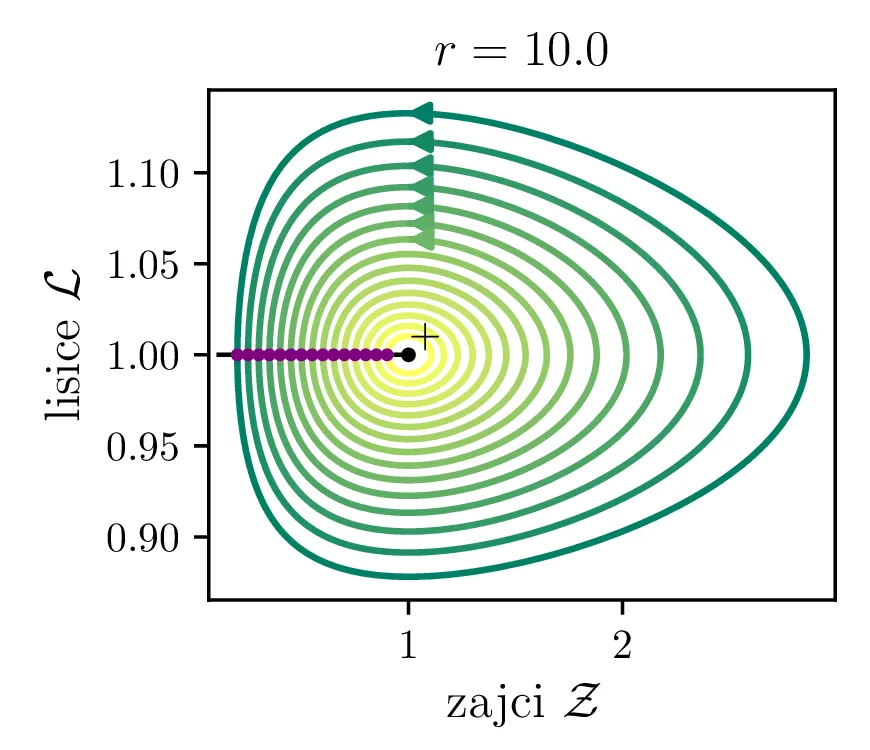
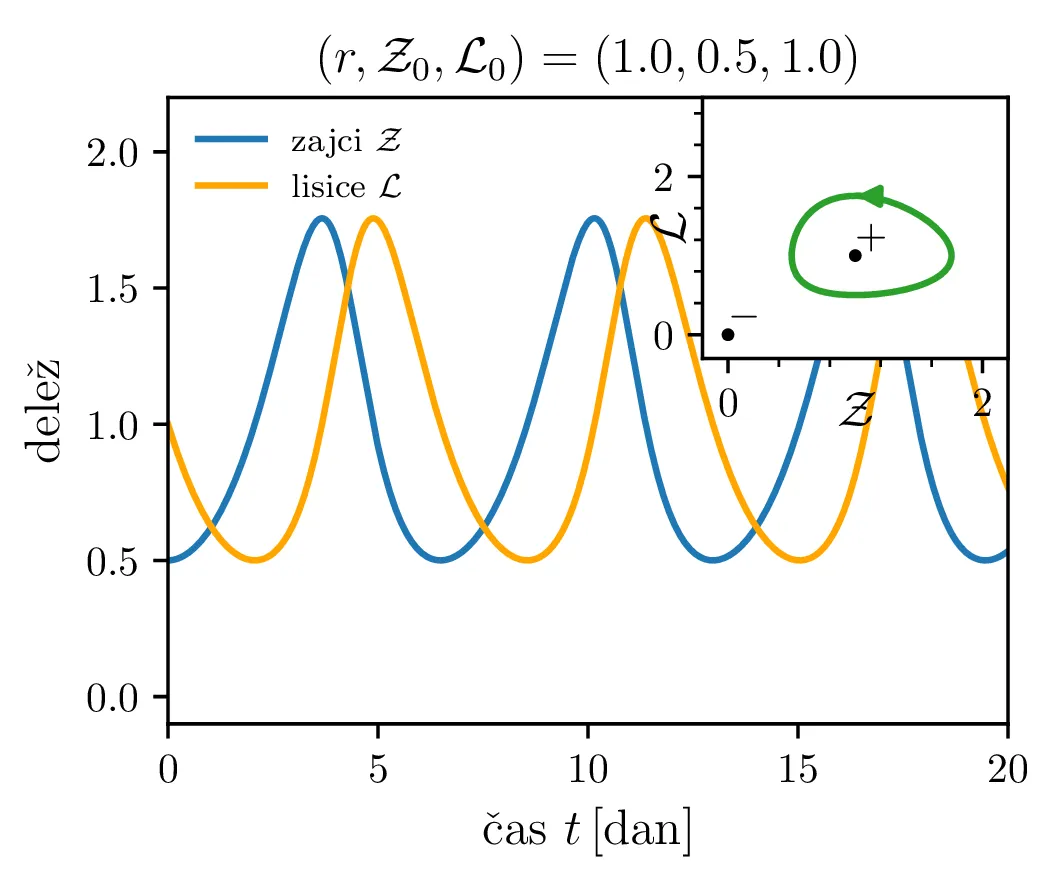
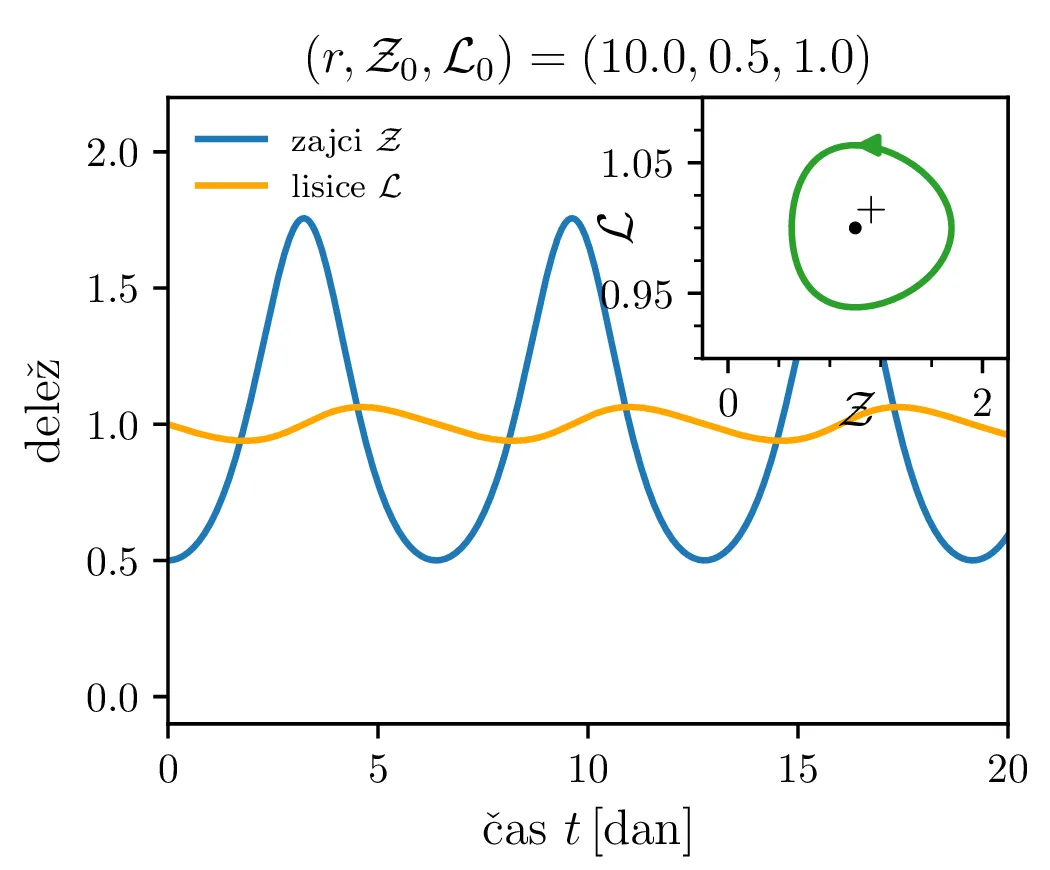
To je stacionarna točka, kjer izumrejo tako plen kot tudi plenilci (\(\mathcal{Z}= 0\) in \(\mathcal{L}= 0\), prva slika 9). Če smo točno v \((\mathcal{Z}, \mathcal{L}) = (0, 0)\), nimamo več dinamike, saj sta obe vrsti izumrli. A če ostane le en zajec, se bo dinamika ponovila. Taka stacionarna točka je nestabilna, saj se za nek poljubno majhen \(\varepsilon > 0\) začetna točka \(T = T^{-} + \varepsilon\) odpelje daleč stran od začetne točka. Za razliko od tega je \[\text{ravnovesje: } T^{+} = (1, 1),\] ki označuje ravnovesje populacij plenilca in plena, stabilna stacionarna točka. \begin{equation}\text{ravnovesje: } Z = \frac{\delta}{\gamma}, \quad L = \frac{\alpha}{\beta}. \label{eq:ravnovesje}\end{equation} Za vsak \(\delta > 0\) namreč obstaja tak \(\varepsilon > 0\), da bo dinamika, ki jo porodi začetna točka \(T = T^{+} + \varepsilon\) ostala v \(\delta\) okolici \(T^{+}\). Pripadajoč Jakobian je \[J(r, 0, 0) = \begin{bmatrix} 0 & -r \\ r^{-1} & 0 \end{bmatrix},\] in ker so njegove lastne vrednosti iz \(\lambda^2 + 1 = 0\) le imaginarne \(\lambda = \pm i\), so po teoriji (glej npr. 4. poglavje v [3]) trajektorije v okolici te točke cikli podobni krožnicam. To tudi vidimo na slikah 9. Časovne poteke takih trajektorij vidimo v drugi (časovni) obliki na 11.
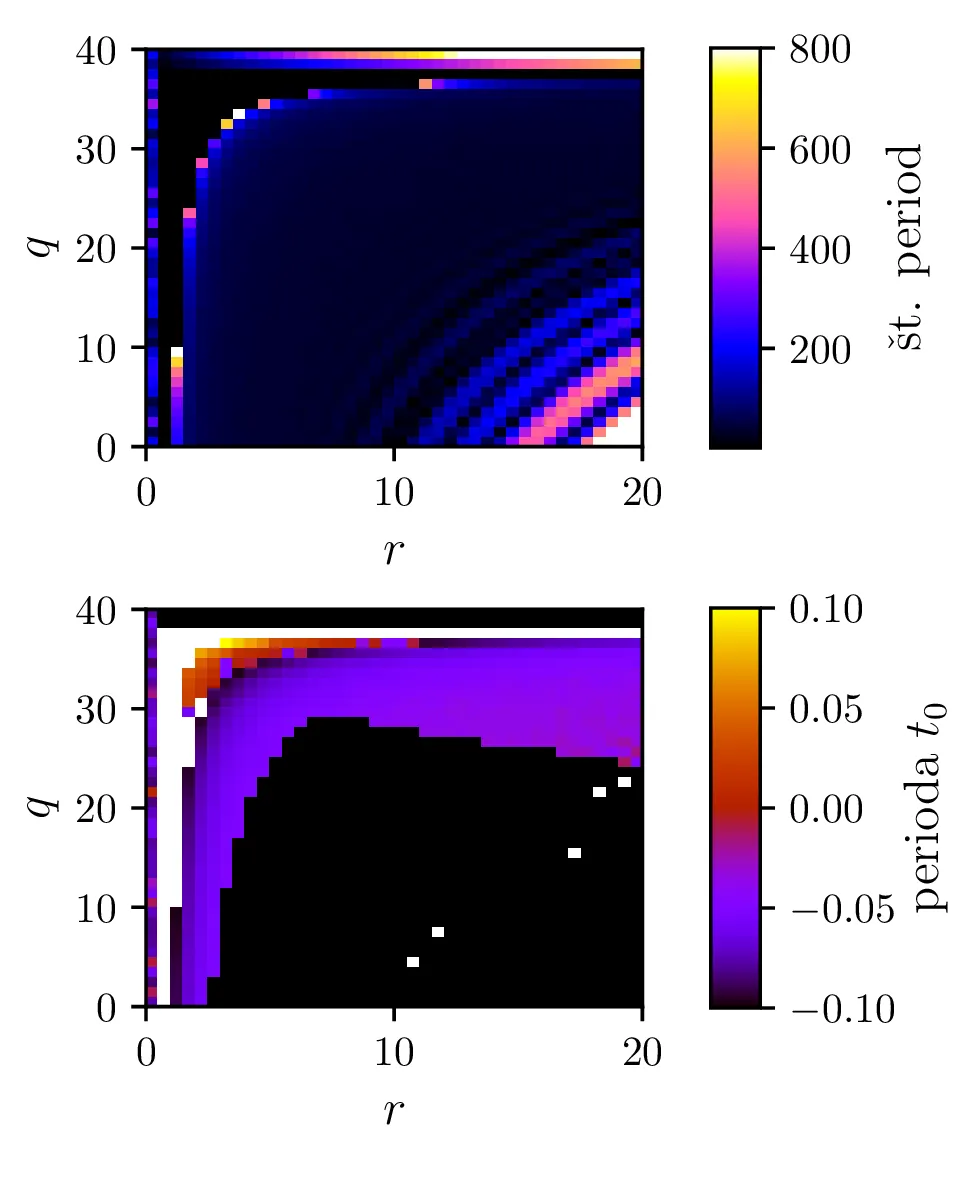
Odvisnost časovne periode
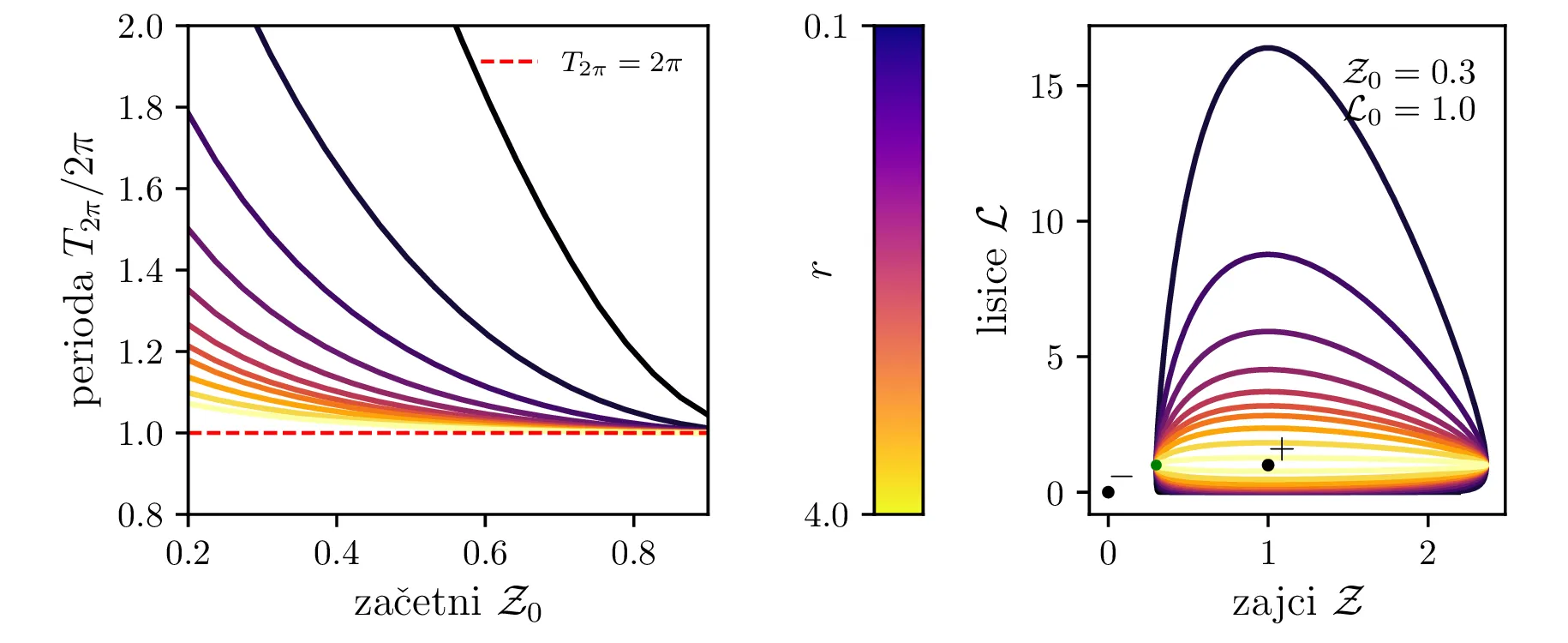
Različne trajektorije, ki označujejo različne \(r\) oz. različne začetne pogoje imajo različne obhodne čase. Seveda je v analogiji z krožnico pričakovano, da je bodo zaključene trajektorije, ki potekajo dlje od stacionarne točke \((1, 1)\), imele daljši obhodni čas (manjši \(\mathcal{Z}_0\) ob \(\mathcal{L}_0 = 1\) pomeni večji obhodni čas, glej sliko 10). Poleg tega pa je ta odvisnost mnogo bolj izražena (obhodni časi so večji in predvsem hitreje naraščajo z manjšim \(\mathcal{Z}_0\) ob \(\mathcal{L}_0 = 1\), spet glej sliko 10).
Poseg v okolje, časovno odvisni parametri
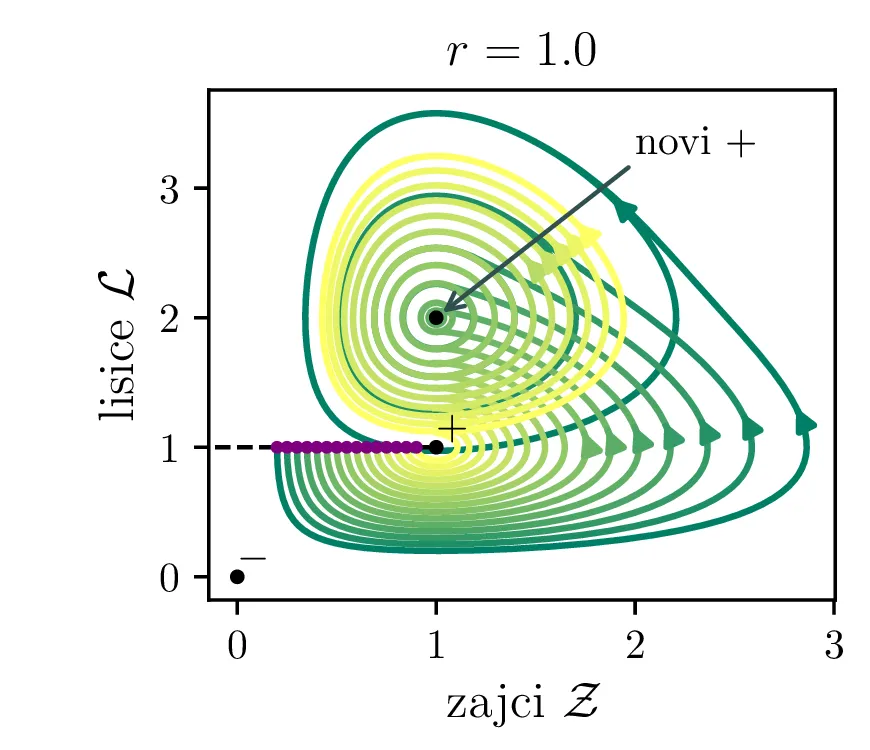
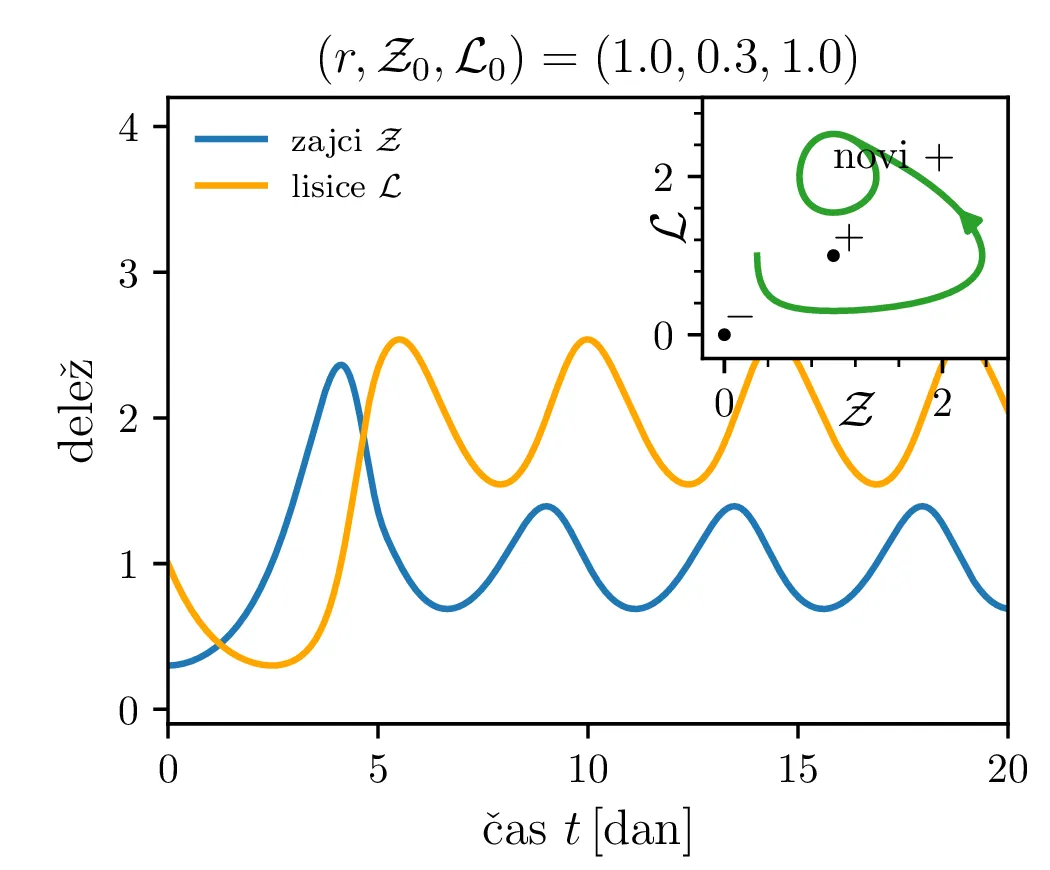
Poglejmo si, kako se sistem odzove na poseg v okolje, npr. večje izobilje hrane za plen. Pri tem se poveča \(\alpha\) faktor, kar bomo v brezdimenzijskem sistemu modelirali z časovno odvisnim \(A(\tau)\), kot v enačbi \begin{equation}\begin{aligned} \dot{\mathcal{Z}} &= r \left( A(\tau) \mathcal{Z}- \mathcal{Z}\mathcal{L}\right), \nonumber \\ \dot{\mathcal{L}} &= r^{-1} \left( \mathcal{Z}\mathcal{L}- \mathcal{L}\right). \label{eq:LV-nondim-A} \end{aligned}\end{equation} Že iz brezdimenzijskih enot \(L_0\) in \(Z_0\) (enačba (6)), še lepše pa iz faznega diagrama (prva slika 12) se vidi, da bo sprememba \(\alpha\) (ali pa \(\beta\)) nekoliko neintuitivno vplivala le pa populacijo plenilcev. Boljši pogoji za plen se torej prevedejo le na boljše pogoje za plenilce. Obratno bi bolj dolgoživ plenilec pomenil le povečanje populacije plena.
Nosilnost okolja za plen in sitost plenilcev
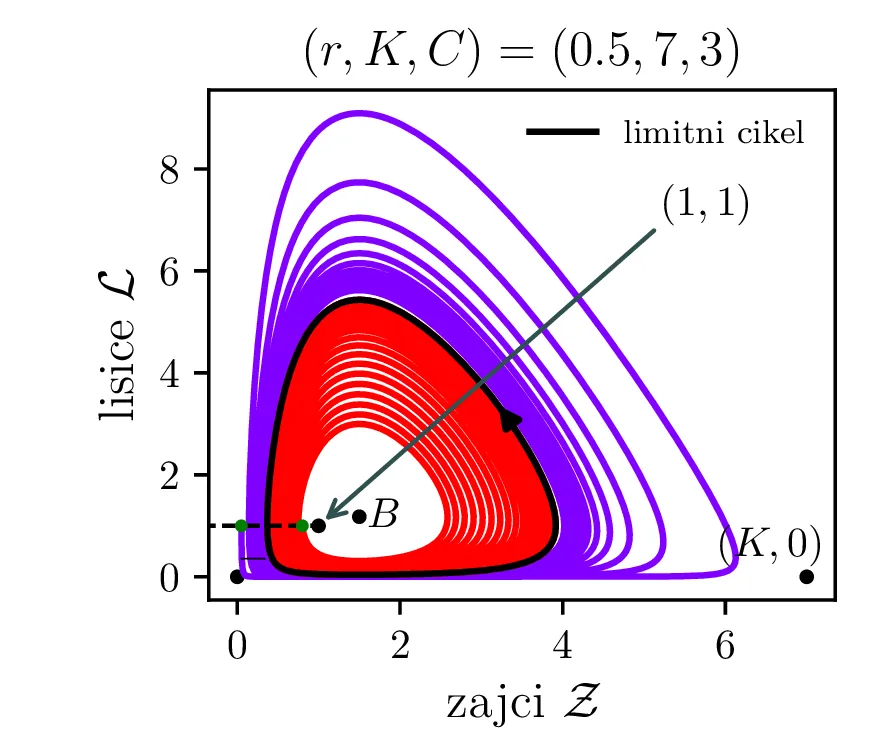
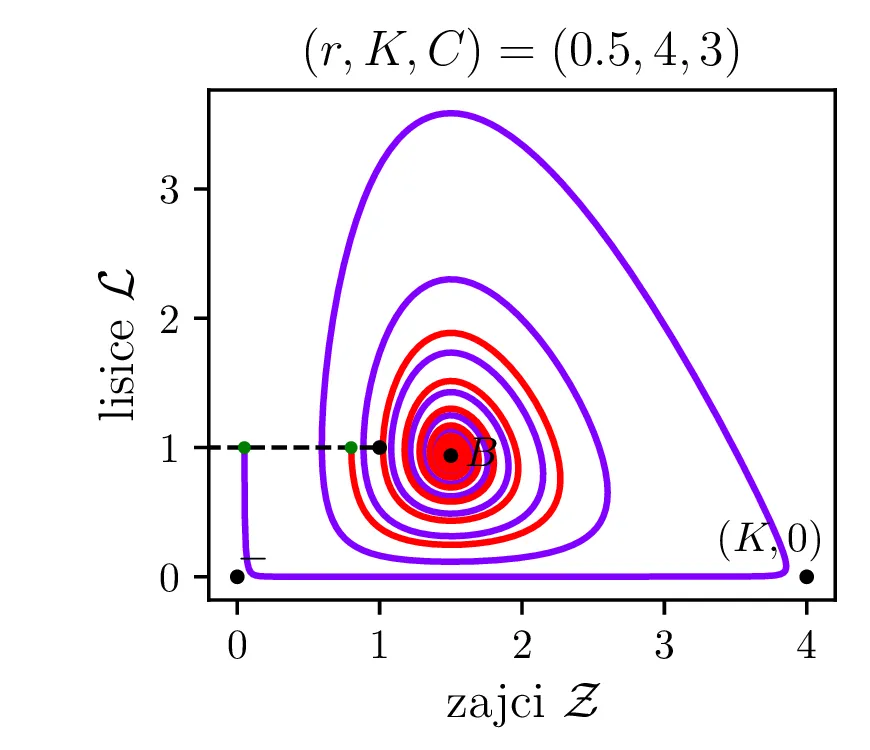
V model želimo vključiti nekaj dodatnih realističnih obnašanj, ki bi jih lahko pričakovali v takem biološkem sistemu. Prvo upoštevamo končno nosilnost (ang. carrying capacity) okolja za populacijo plena \(K\). Člen, ki označuje razmnoževanje plena torej dopolnimo kot \[\mathcal{Z}\to \mathcal{Z}\left( 1 - \frac{\mathcal{Z}}{K} \right).\] Tako se bo za \(\mathcal{Z}\to K\) plen vedno manj učinkovito množil, saj morajo posamezniki (zajci) v populaciji tekmovati med sabo za potrebne vire. \[\mathcal{Z}\mathcal{L}\to \mathcal{Z}\mathcal{L}\left( \frac{1}{1 + \mathcal{Z}/ C} \right),\] pri čemer smo dodali faktor \(\left( \frac{1}{1 + \mathcal{Z}/C} \right)\), ki se zasiči za \(\mathcal{Z}\ll C\) in tako modelira diminishing return vrednost dodatnega plena, ko je plenilec že sit. Lotka-Volterra sistem zdaj dobi obliko \begin{equation}\begin{aligned} \dot{\mathcal{Z}} &= r \left( \mathcal{Z}\left( 1 - \frac{\mathcal{Z}}{K} \right) - \frac{\mathcal{Z}\mathcal{L}}{1 + \mathcal{Z}/ C} \right), \nonumber \\ \dot{\mathcal{L}} &= r^{-1} \left( \frac{\mathcal{Z}\mathcal{L}}{1 + \mathcal{Z}/ C} - \mathcal{L}\right). \label{eq:LV-improved} \end{aligned}\end{equation} Za tako modificiran Lotka-Volterra sistem imamo namesto dveh stacionarnih točk \((0, 0)\) in \((1, 1)\) zdaj nov set treh stacionarnih točk. Še vedno je prisotna fiksna točka izumrtja \((0, 0)\), prisotna pa je tudi stacionarna točka \((K, 0)\), kjer je populacija zajcev \(\mathcal{Z}= K\) enaka nosilnosti okolja, plenilca pa ni. Za dinamiko sistema pa je pomembna stacionarna točka \begin{equation}B = \left( \frac{C}{C - 1}, \frac{C (KC - K - C)}{K(C-1)^2} \right), \label{eq:B}\end{equation} ki v grobem prevzame vlogo stacionarne točke ravnovesja (točka \(+\) oz. \((1, 1)\), glej enačbo (9)). A točka \(B\) je zdaj odvisna od parametrov \(K, C\), dinamika v njeni okolici pa je bolj zanimiva. Zapišemo njen Jakobian \[J_B = J(r, \mathcal{Z}_B, \mathcal{L}_B) = \begin{bmatrix} r \left( 1 - \frac{2\mathcal{Z}}{K} - \frac{C^2 \mathcal{L}}{(\mathcal{Z}+ C)^2} \right) & -\frac{rC \mathcal{Z}}{\mathcal{Z}+ C} \\ \frac{C^2 \mathcal{L}}{r (C + \mathcal{Z})^2} & \frac{C\mathcal{Z}- C - \mathcal{Z}}{r(C + \mathcal{Z})} \end{bmatrix}.\]
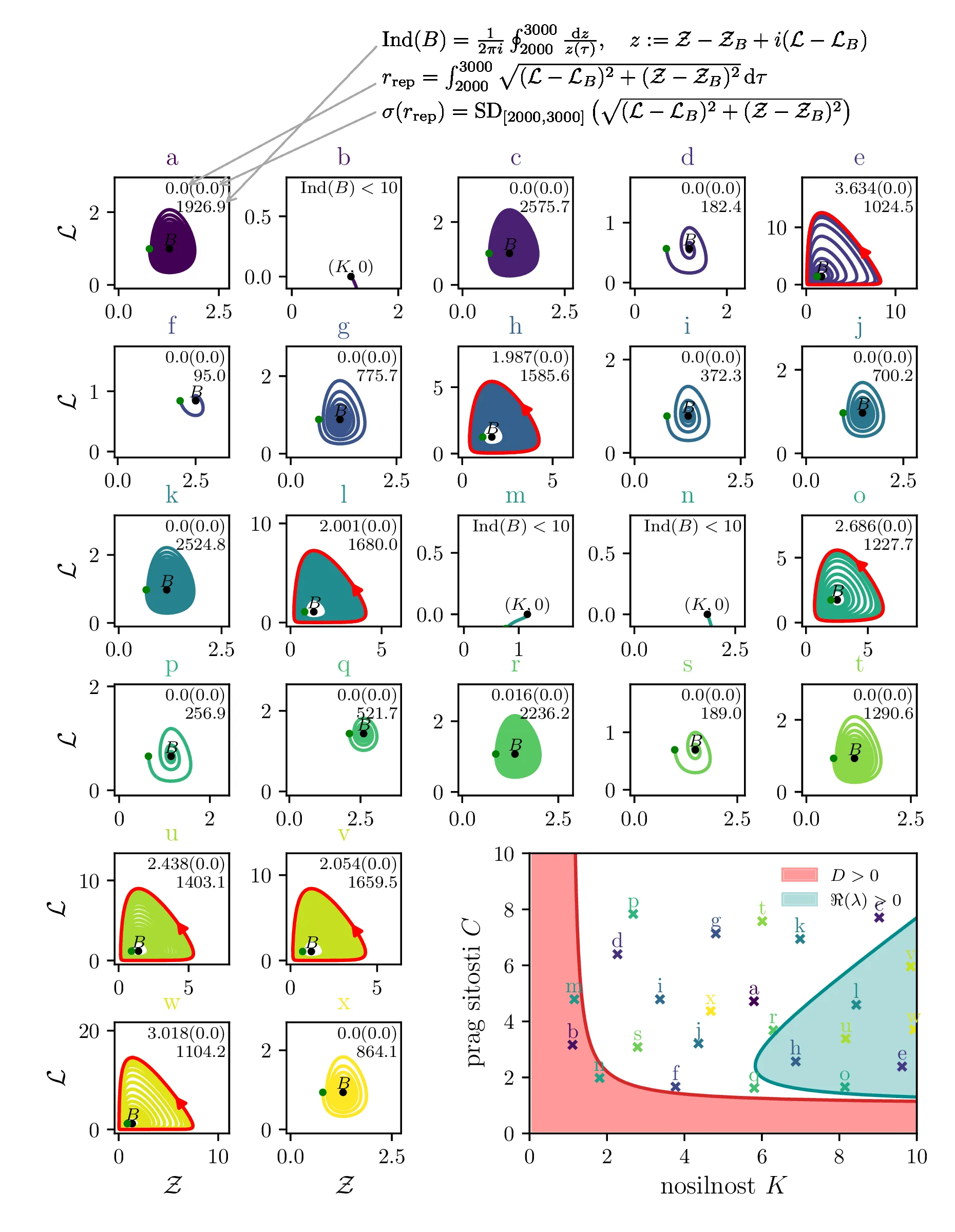
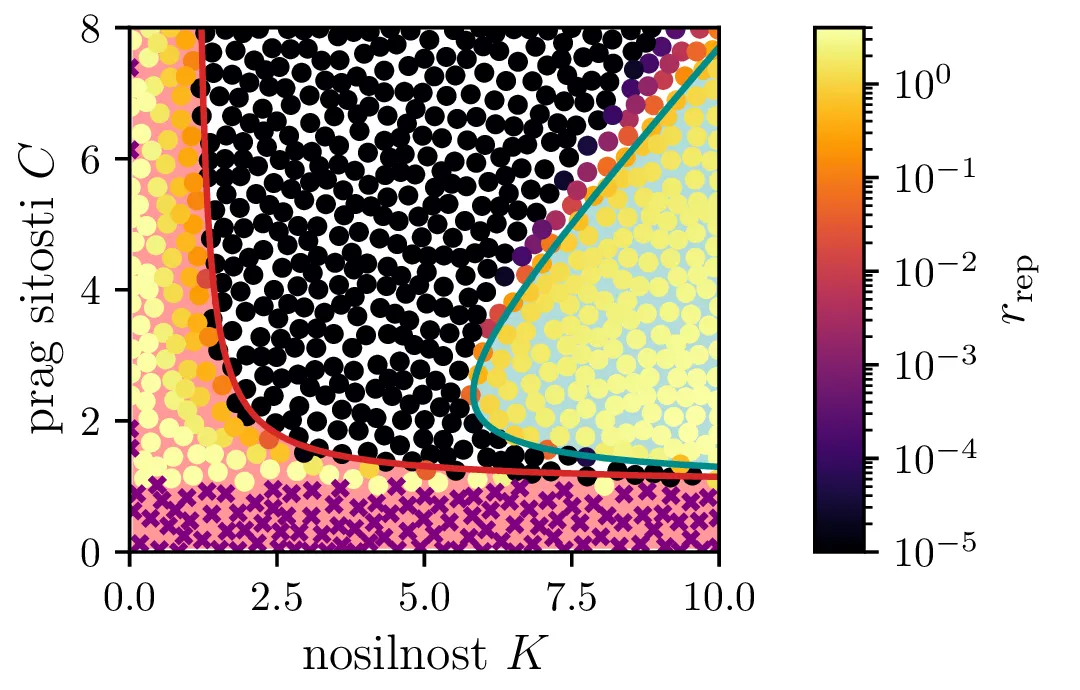
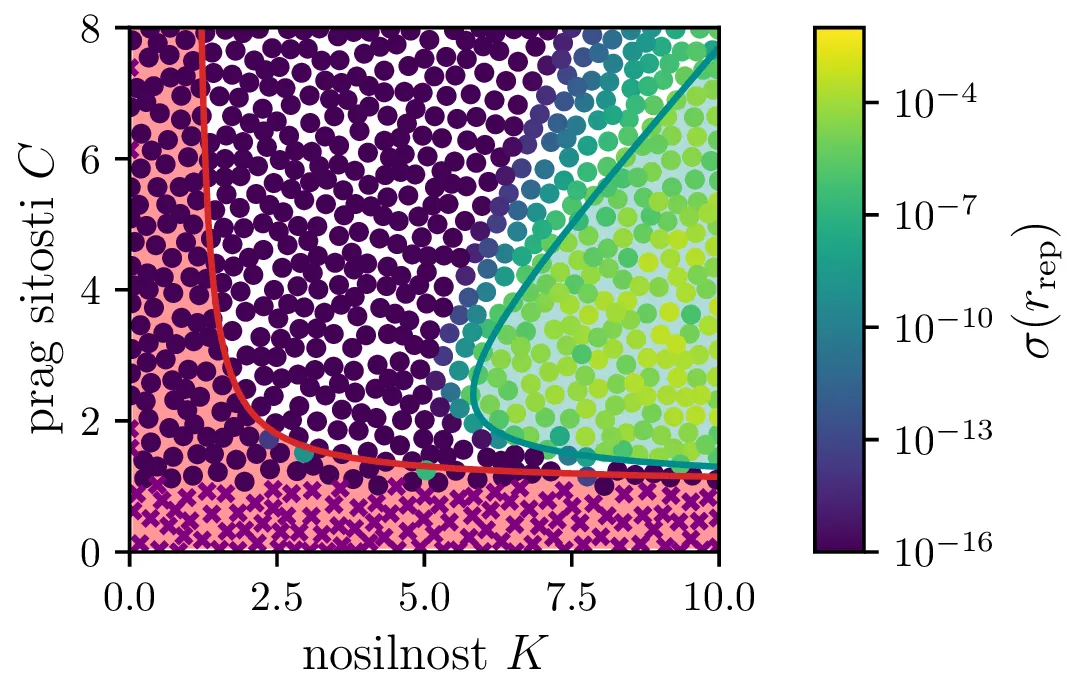
Na podlagi lastnih vrednosti \(\lambda_i\) tega Jakobiana bomo karakterizirali obnašanje okoli točke \(B\). Glede na rešitve karakterističnega polinoma \begin{equation}p_B(\lambda) = 1 - \frac{1}{C} - \frac{1}{K} + \frac{r(C + C^2 + K - CK)\lambda}{(C-1)CK} + \lambda^2 = 0, \label{eq:quadratic}\end{equation} ločimo tri možnosti [3]
-
Vse lastne vrednosti vrednosti \(\lambda_i \in \mathbb{R}\). Tedaj je točka fiksna točka, njena stabilnost pa je določena s pozitivno definitnostjo Jakobiana. Za kvadratni karakteristični polinom \(p_B(\lambda)\) je to ekvivalentno \(D > 0\) (izraz (14), območje narisano z rdečo na tretji sliki 14).
-
Vse lastne vrednosti \(\lambda_i \in \mathbb{C}\) in \(\Re(\lambda_i) > 0\). Tedaj so trajektorije spirale navzven iz fiksne točke. Ravno tu opazimo limitne cikle, kot je to jasno ilustrirano na sliki 14 za modro pobarvano območje.
-
Vse lastne vrednosti \(\lambda_i \in \mathbb{C}\) in \(\Re(\lambda_i) < 0\). Tedaj so trajektorije spirale v fiksno točko. To je spet jasno ilustrirano na tretji sliki 14 za nepobarvano območje med rdečim in modrim.
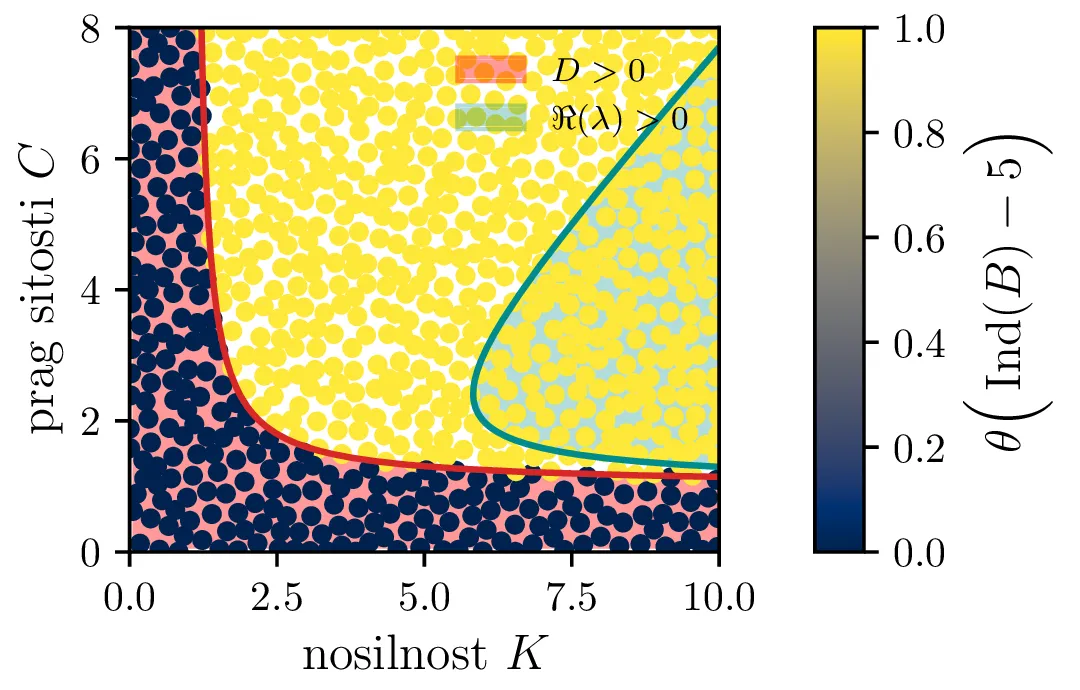
Te tri možnosti bomo ločili z uporabi diskriminante za (13) \begin{equation}D = \frac{4CK(C+K - CK) + \frac{r^2}{(C-1)^2} (C + C^2 + K - CK)}{C^2 K^2}, \label{eq:disc}\end{equation} ki jo uprizorimo na sliki 14 desno spodaj z rdečim območjem \(D > 0\). Da ločimo spirale navznoter in spirale navzven bomo uporabili tudi količino, ki je sorazmerna \(\Re(\lambda_i)\), sicer \[\Re(\lambda_i) \propto - C- K + CK + C^2,\] kar narišemo kot modro območje \(\Re(\lambda_i) < 0\) na sliki 14 desno spodaj.
Limitni cikli
Na podlagi diskriminante in kriterija \(\Re(\lambda_i) < 0\) lahko zdaj opazimo, kdaj se v faznem poteku pojavijo limitni cikli. Na sliki 14 so narisani fazni diagrami , t. j. izven območje \(D > 0\) in hkrati v območju \(\Re(\lambda_i) < 0\).
Fotoni v laserju
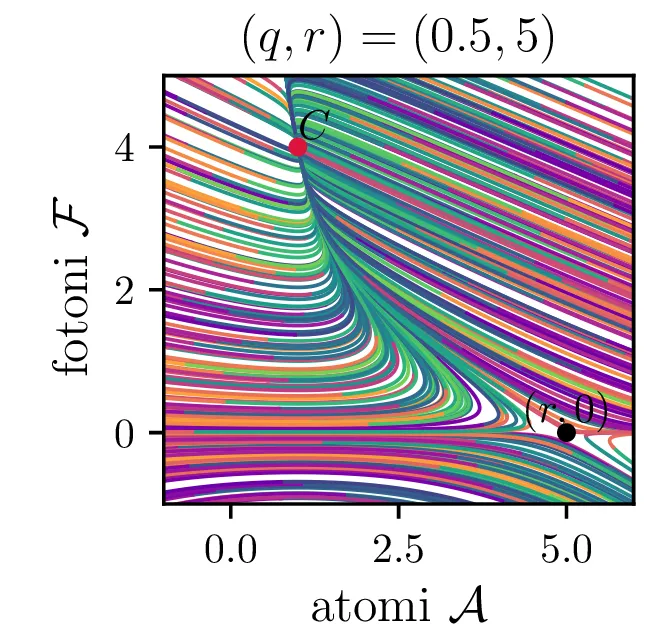
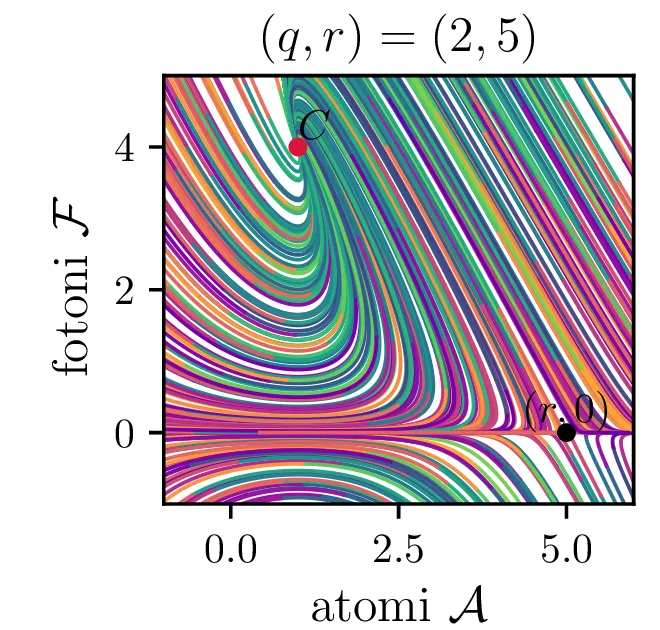
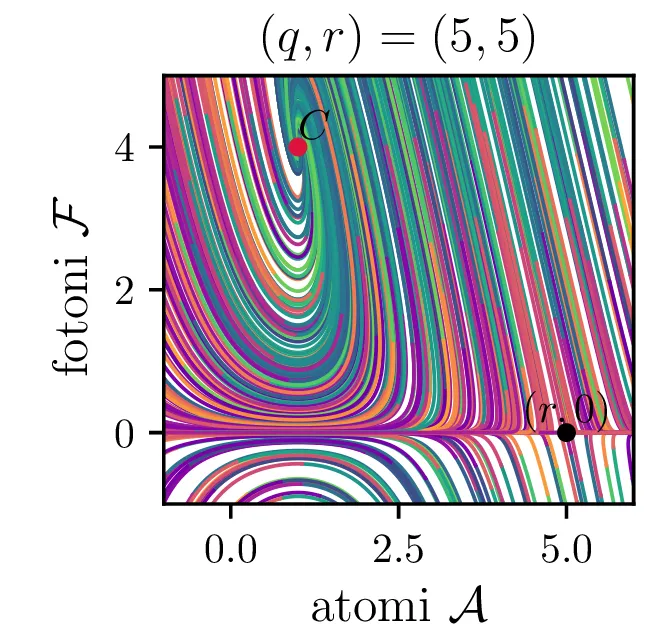
Laser opišemo kot snov, sestavljeno iz števila atomov \(a\), ki jo stalno vzbujamo, pri tem pa vzbujena stanja \(a\) stalno prehajajo nazaj v osnovna stanja s tem, da oddajo fotone svetlobe \(f\). To opisuje sistem dveh navadnih diferencialnih enačb \begin{equation}\begin{aligned} \dot{a} &= R - B_2 fa - \beta a, \nonumber \\ \dot{f} &= -\alpha f + B_1 fa. \label{eq:laser} \end{aligned}\end{equation} Ta sistem ima dve fiksni točki. Prva je točka, kjer imamo zgolj atome (\(f = 0\)), saj vzbujena stanja ustvarjamo ravno dovolj hitro, da kompenziramo razpadanje \[\text{nezadostno črpanje brez fotonov: } \left( \frac{R}{\beta}, 0 \right).\] Druga kritična točka \((a, f)\) je \[\text{ravnovesna fiksna točka } C = \left( \frac{B_1 R - \alpha\beta}{B_2 \alpha}, \frac{\alpha}{B_1} \right),\] na podlagi katere bomo izbrali nove karakteristične dimenzije \[R_0 = \frac{\alpha\beta}{B_1}, \quad A_0 = \frac{\alpha}{B_1}, \quad F_0 = \frac{\beta}{B_2}, \quad t_0 = \frac{1}{\beta},\] s katerimi vpeljemo brezdimenzijske količine \[R = R_0 r, \quad a = A_0 \mathcal{A}, \quad f = F_0 \mathcal{F}, \quad t = t_0 \tau,\] v katerih sistem enačb (15) ob uvedbi \[q = \frac{\alpha}{\beta},\] zavzame obliko \begin{equation}\begin{aligned} \dot{\mathcal{A}} = r - \mathcal{F}\mathcal{A} - \mathcal{A}, \nonumber \\ \dot{\mathcal{F}} = q \left( \mathcal{F}\mathcal{A} - \mathcal{F} \right). \label{eq:laser-nondim} \end{aligned}\end{equation}
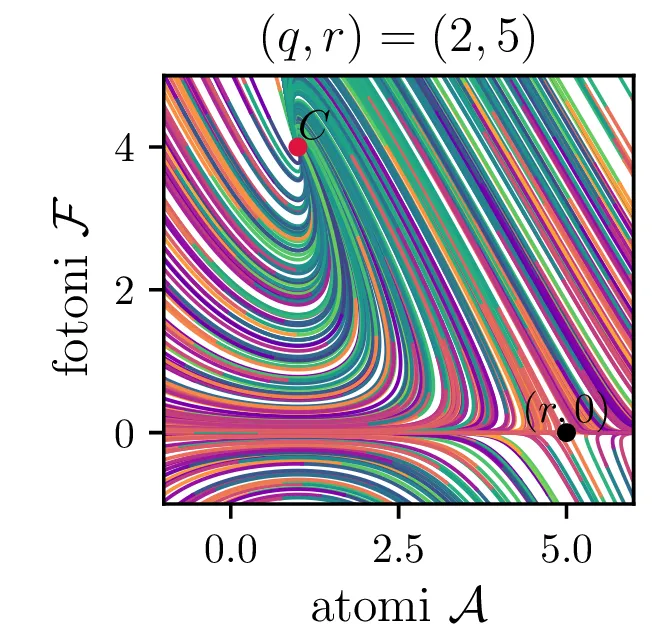
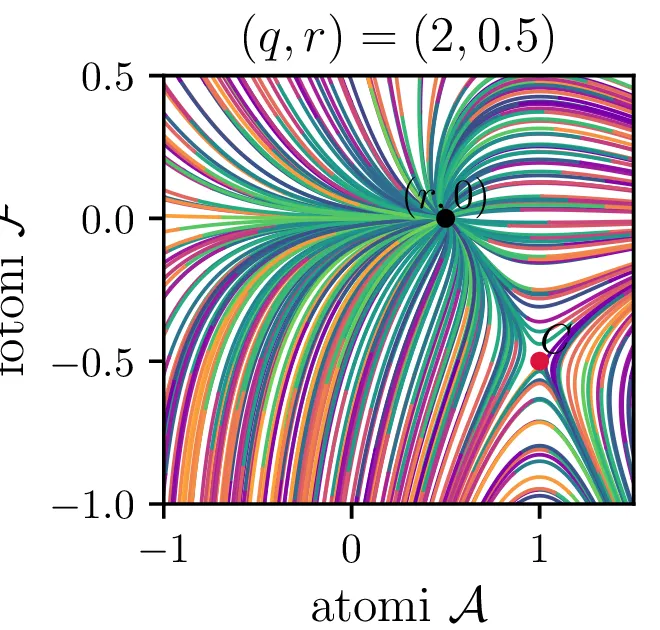
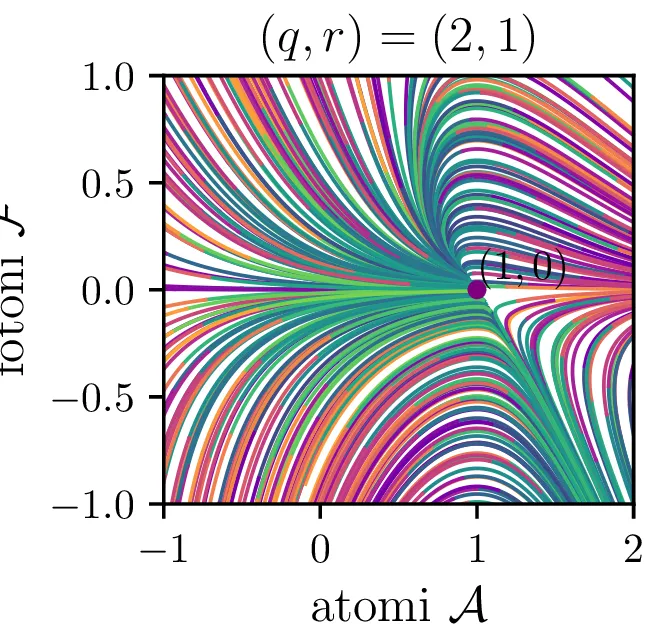
V novih brezdimenzijskih \((\mathcal{A}, \mathcal{F})\) sta fiksni točki podani kot \[\begin{aligned} \text{nezadostno črpanje brez fotonov: } \left( r, 0 \right), \\ \text{ravnovesna fiksna točka } C = \left( 1, r-1 \right). \end{aligned}\] Jakobian v fiksni točki \((r, 0)\) je \[J(r, 0) = \begin{bmatrix} -1 & -r \\ 0 & q(r-1) \end{bmatrix},\] za kar preprosto izračunamo diagonalizacijo \[J(r, 0) = P \begin{bmatrix} -1 & 0 \\ 0 & q(r-1) \end{bmatrix} P^{-1}, \quad P = \begin{bmatrix} 1 & 0 \\ \frac{-r}{1 - q + qr} & 1 \end{bmatrix},\] na podlagi katere lahko za fiksno točko ločimo naslednje možnosti:
-
Če je \(r > 1\), je \((r, 0)\) sedlo in nestabilna fiksna točka sistema (16). Glej prvo sliko 16.
-
Če je \(r < 1\), je \((r, 0)\) stabilna fiksna točka sistema (16). Glej drugo sliko 16.
-
Če je \(r = 1\), je \((1, 0)\) sedlo za Gaussovsko ukrivljenostjo 0. Tedaj je tudi druga fiksna točka \(C\) ista točka. Glej tretjo sliko 16.
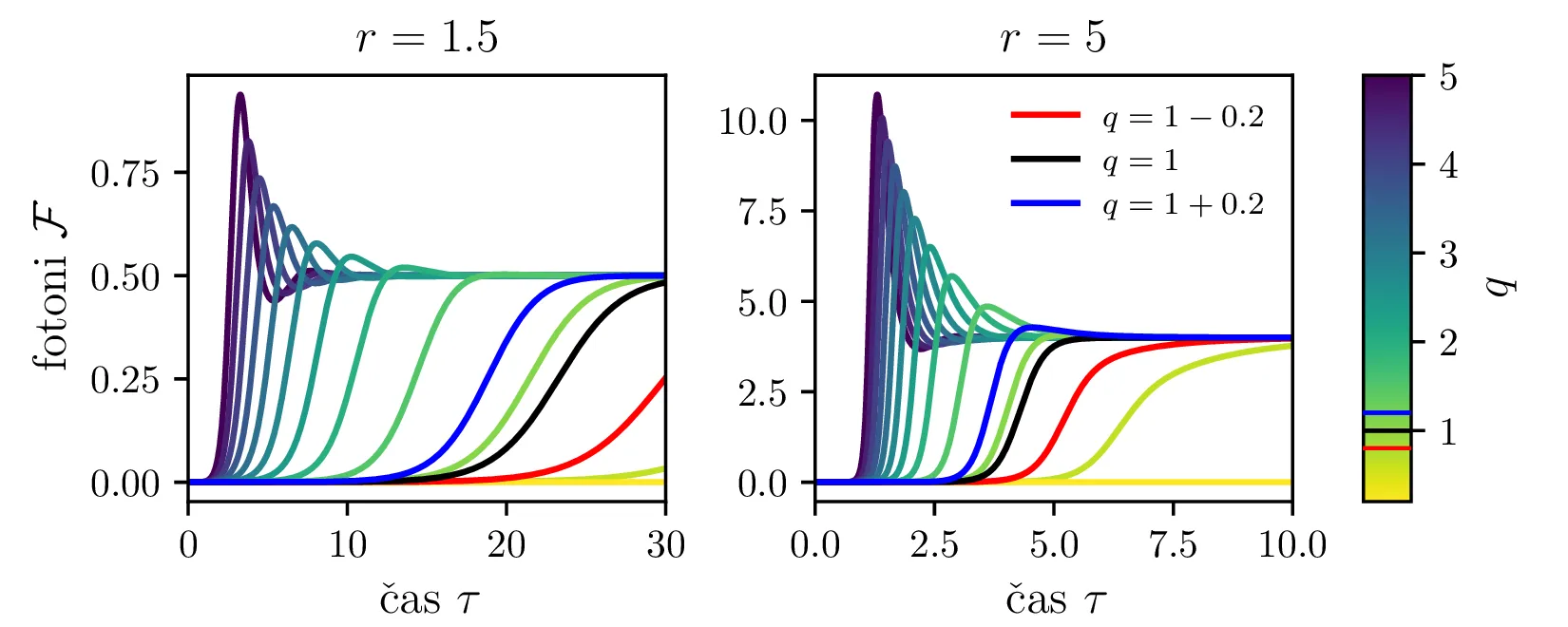
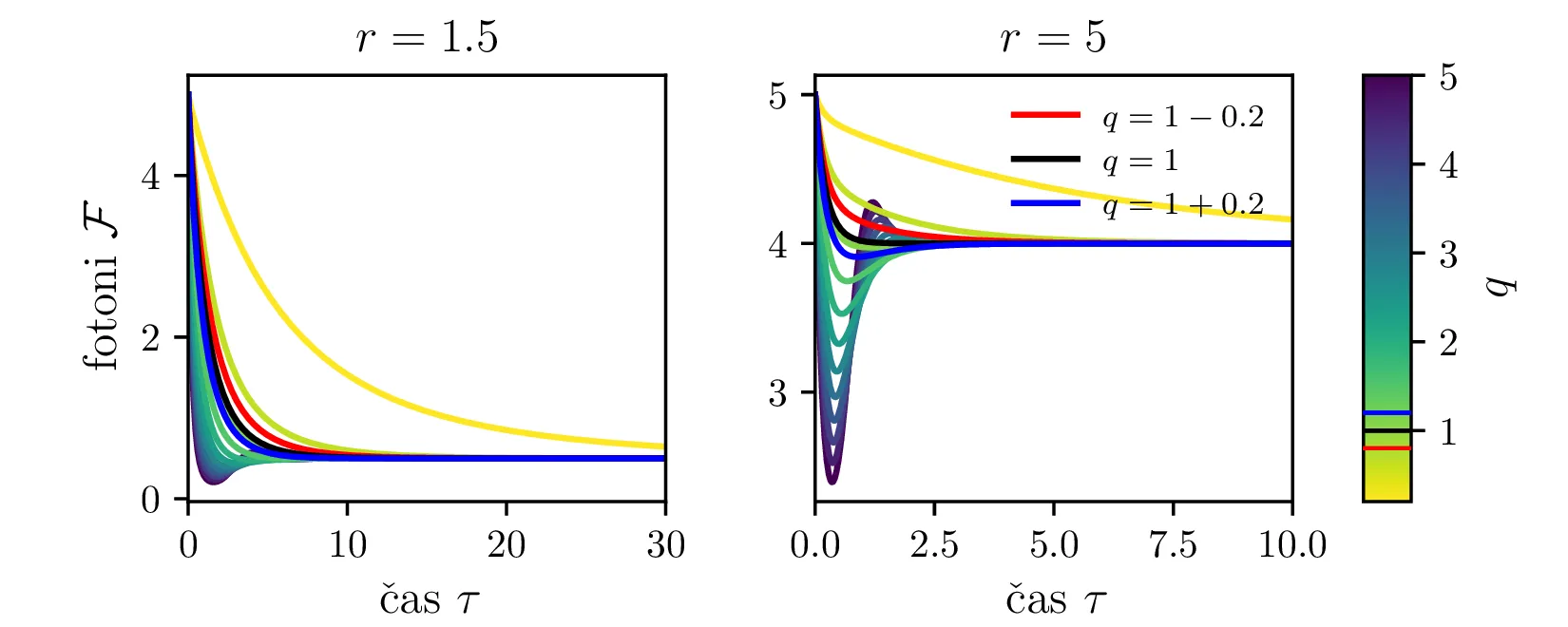
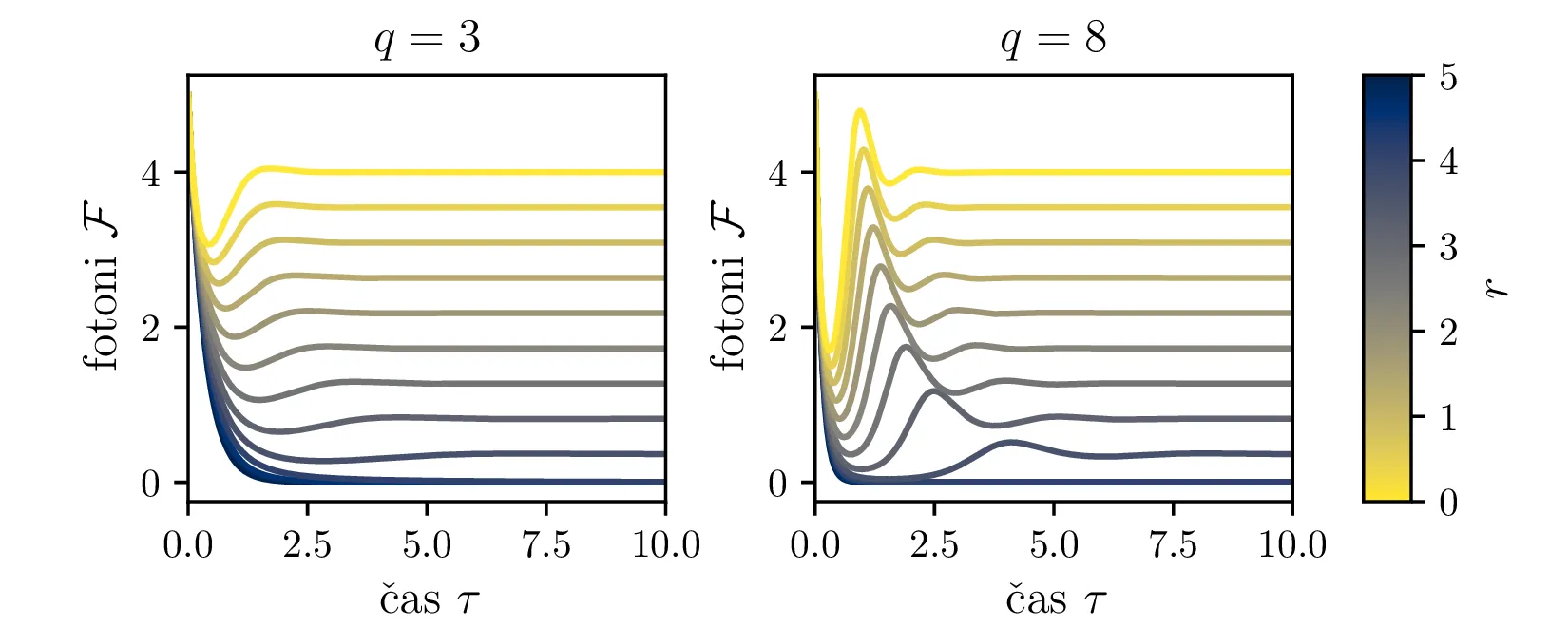
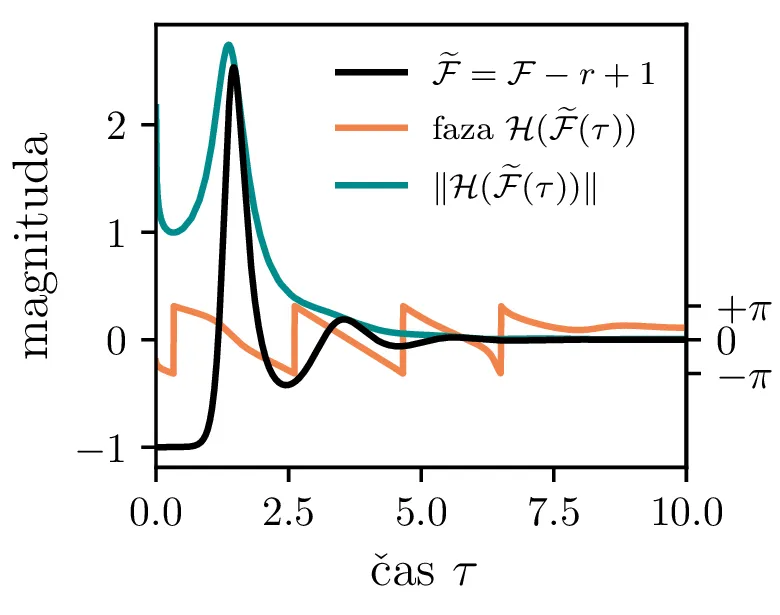
Iz slike 16 lahko vidimo, da ima sistem v točkah \((r, 0)\) in točki \(C\) dve ravnovesji. Kateremu ravnovesju se približuje v \(t \to \infty\) pa je odvisno predvsem od moči črpanja. Za črpanja \(r > 1\) se bo laser približeval točki \(C\), v kateri imamo neko število fotonov \(\mathcal{F} = r-1\). Potek približevanja temu ravnovesju za različne \(q\) lahko vidimo na sliki 17. Nasprotno bo za šibko črpanje \(r < 1\) pa bo populacija fotonov ne glede na začetno zamrla proti 0 (npr. slika 16).
To lahko vidimo tudi iz analize fiksne točke \(C = (1, r-1)\), v kateri je karakteristični polinom Jakobiana \[\lambda^2 + r\lambda + qr - q = 0,\] iz česar lahko določimo lastni vrednosti \[\lambda_{1,2} = -\frac{r}{2} \pm \sqrt{q - qr + \frac{q^2}{4}}.\] Prvo predpostavimo, da je diskriminanta v tej rešitvi pozitivna. Če zapišemo diskriminanto pod korenom kot \(r^2 - q(r-1)\), je jasno, da velja:
-
Za \(r > 1\) sta \(\lambda_{1,2} < 0\) in je \(C\) stabilna fiksna točka. Glej prvo sliko 16.
-
Za \(r < 1\) sta \(\lambda_{1} > 0\), \(\lambda_{2} < 0\) in je \(C\) nestabilna fiksna točka. Glej drugo sliko 16.
-
Za \(r = 1\) imamo zopet degenerirani primer, kjer sta obe fiksni točki enaki (tretja slika 16).
Kako pa interpretiramo Jakobian, če je diskriminanta negativna, t. j. da je \[q > \frac{r^2}{4(r-1)}.\] Tedaj imamo lastni vrednosti z \(\Re(\lambda_{1,2}) < 0\) in neničelnim imaginarnim delom \(\Im(\lambda_{1,2}) \ne 0\). Taka lastna vrednost narekuje, se trajektorije točki \(C\) približujejo spiralno, ne več kot trajektorije ki so asimptotsko vzporedne z enim od lastnih vektorjev Jakobiana v \(C\). Ta sprememba je vidna na sliki 18.