Thompsonov problem
Numerična nelinearna optimizacija in problem razporeditve nabojev na krogli in drugih površinah
Navodila
-
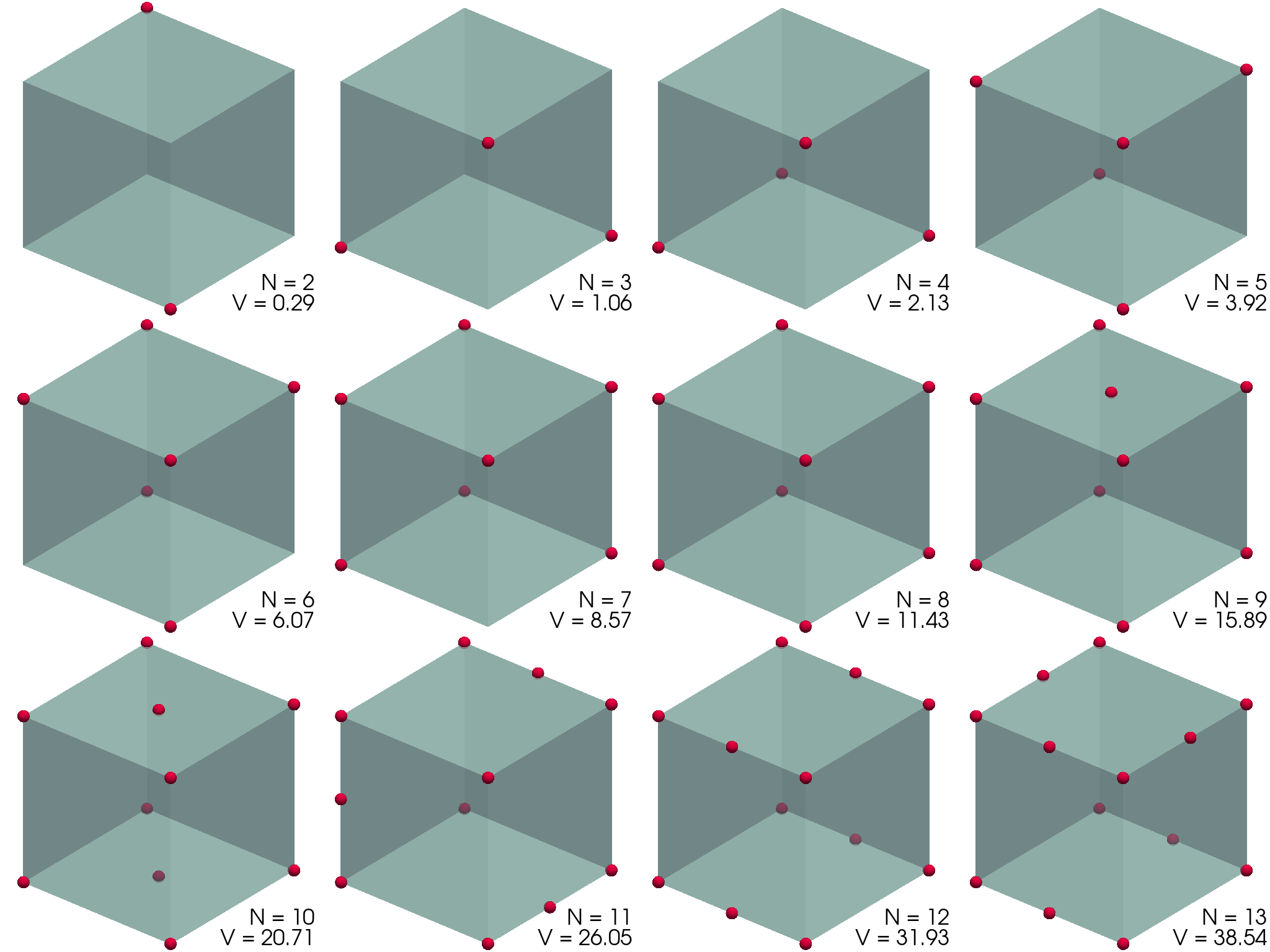
Thomsonov problem: na prevodno kroglo nanesemo N enakih (klasičnih) nabojev. Kako se razmestijo po površini?1 Zahtevamo seveda minimum elektrostatične energije. Primerjaj učinkovitost in natančnost za različne minimizacijske metode, npr. Powellovo ali n-dimenzionalni simpleks (amebo oz. Nelder-Mead).
-
Problem optimalne vožnje skozi semafor, ki smo ga spoznali pri nalogi 1, lahko rešujemo tudi z numerično minimizacijo, če časovno skalo diskretiziramo. Lagrangianu \(\int \dot{v} \,\mathrm{d}{t} − \lambda \int v \,\mathrm{d}{t}\) lahko dodamo omejitev hitrosti v obliki členov \(\mathop{\mathrm{exp}}(\beta(u − u_\text{lim}))\), če hočemo (približno) zagotoviti \(u \le u_\text{lim}\). Izpolnitev pogoja je toliko ostrejša, kolikor večji \(\beta\) vzamemo. Poskusiš lahko tudi druge omejitvene funkcije, na primer kakšno funkcijo s polom. Za iskanje Lagrangeovega multiplikatorja lahko uporabiš bisekcijo ali kakšno drugo vgrajeno metodo za iskanje ničel na funkciji \(l(\lambda) = \int v(\lambda, t) \,\mathrm{d}{t}\), kjer je \(v(\lambda, t)\) rezultat minimizacije pri izbranem \(\lambda\). V tem primeru je enakost izpolnjena eksaktno.
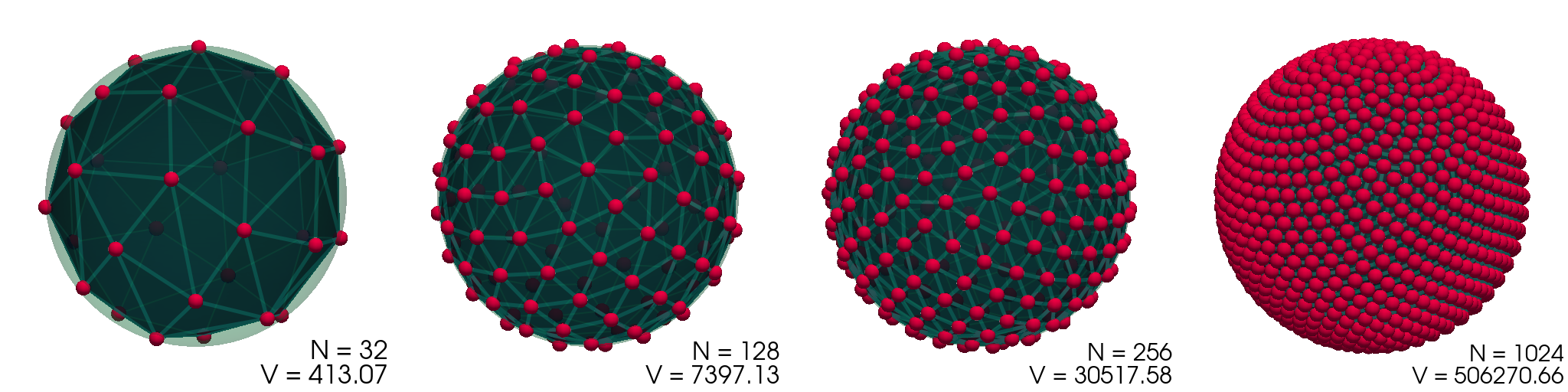
Thomsonov problem
Rešujemo nelinearni minimizacijski, kjer minimiziramo potencialno energijo
\begin{equation}V = \sum_{j < i} \frac{1}{|\mathbf{r}_j - \mathbf{r}_i|}, \label{eq:V}\end{equation}
pri tem pa sta \(\mathbf{r}_i\) in
\(\mathbf{r}_j\) omejena na površino krogle in parametrizirana z enim parom
\((\vartheta, \phi)\), tako da je
\[\mathbf{r} = \begin{pmatrix} \cos{\phi} \sin{\vartheta} & \sin{\phi} \sin{\vartheta} &
\cos{\vartheta} \end{pmatrix}.\]
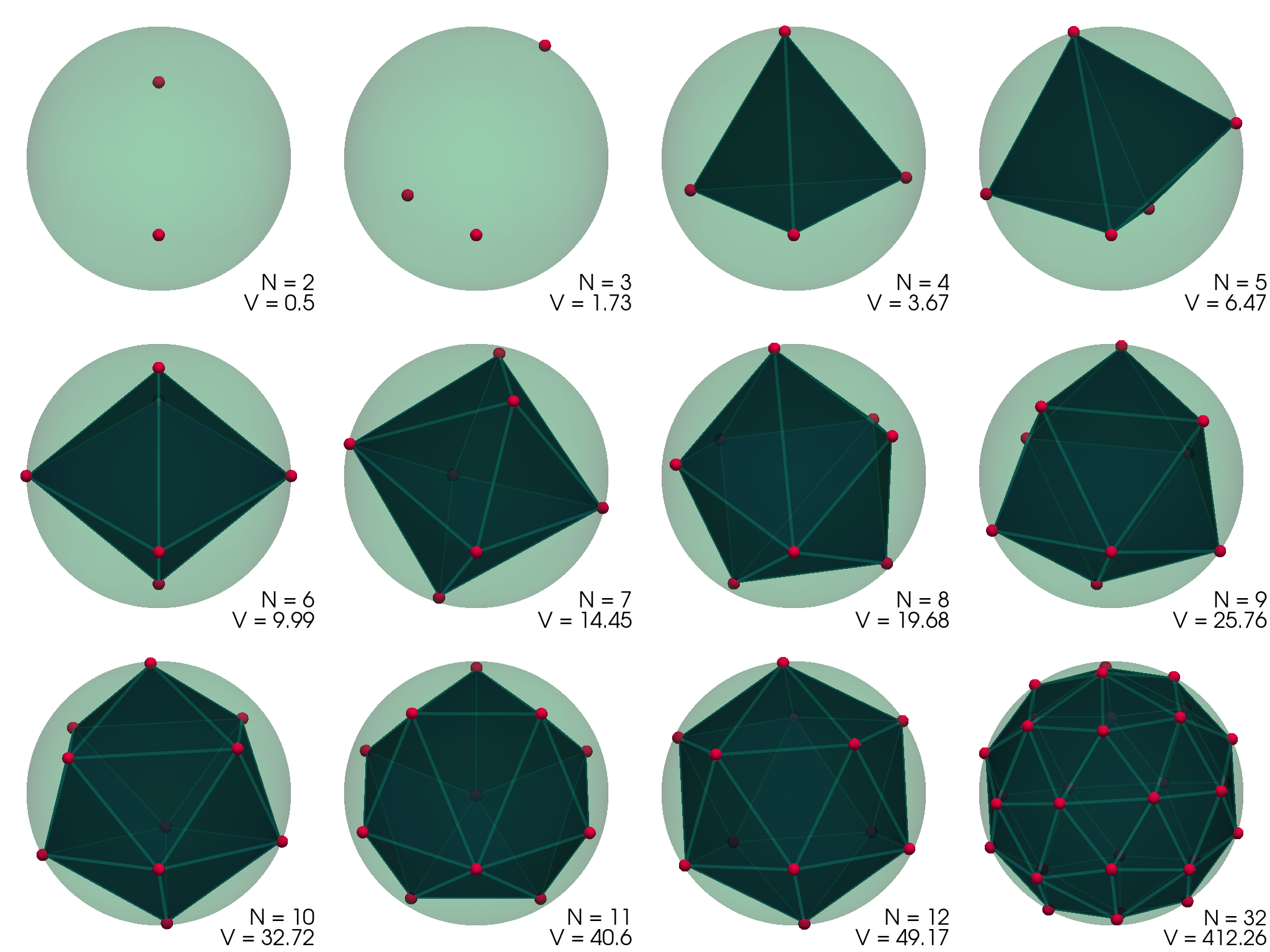
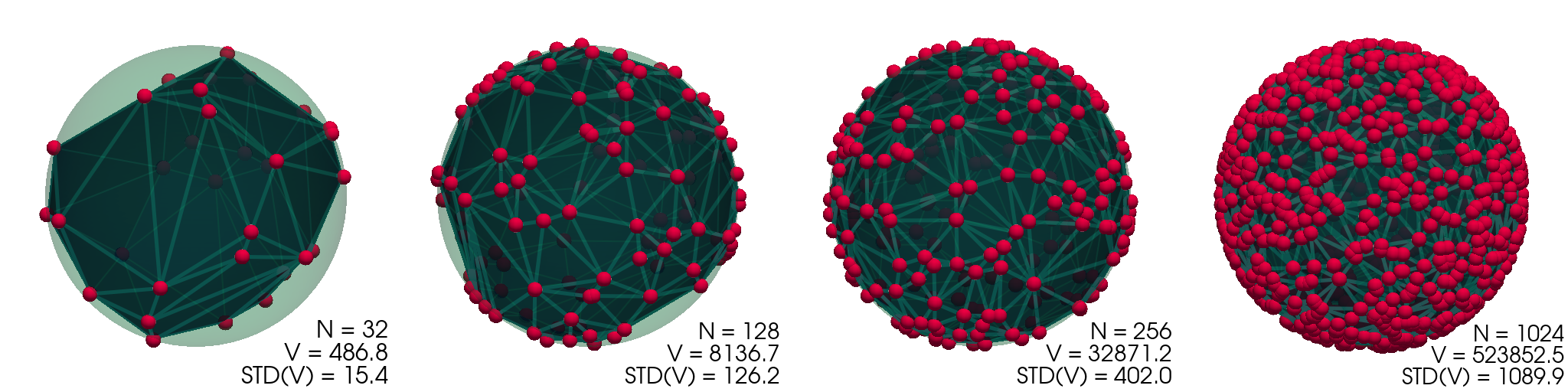
Konfiguracije, ki jih dobimo in njihove konveksne ovojnice (pridobljene z
scipy.spatial.ConvexHull), vidimo prikazane na sliki (1).
Naboji na površini torusa
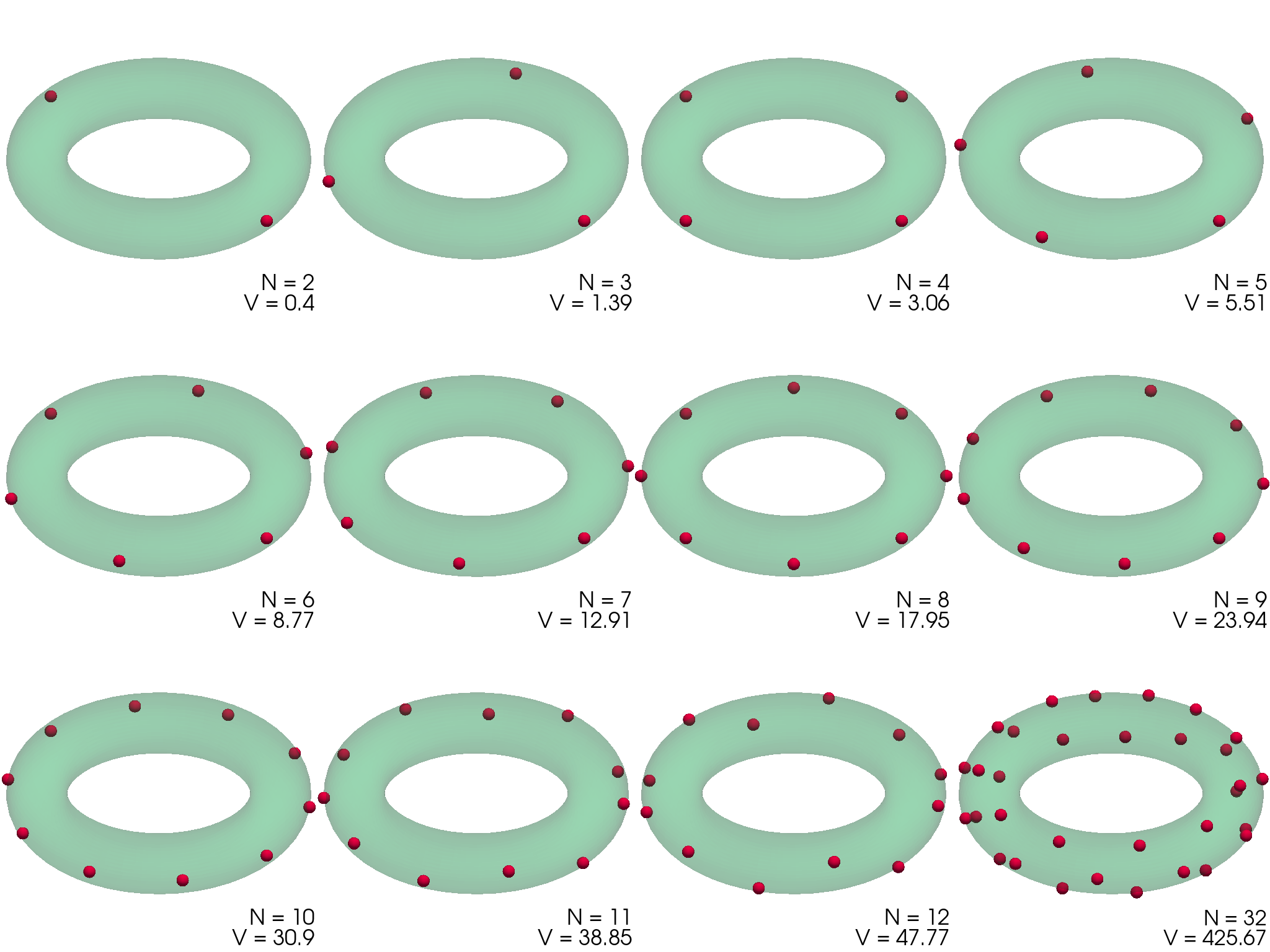
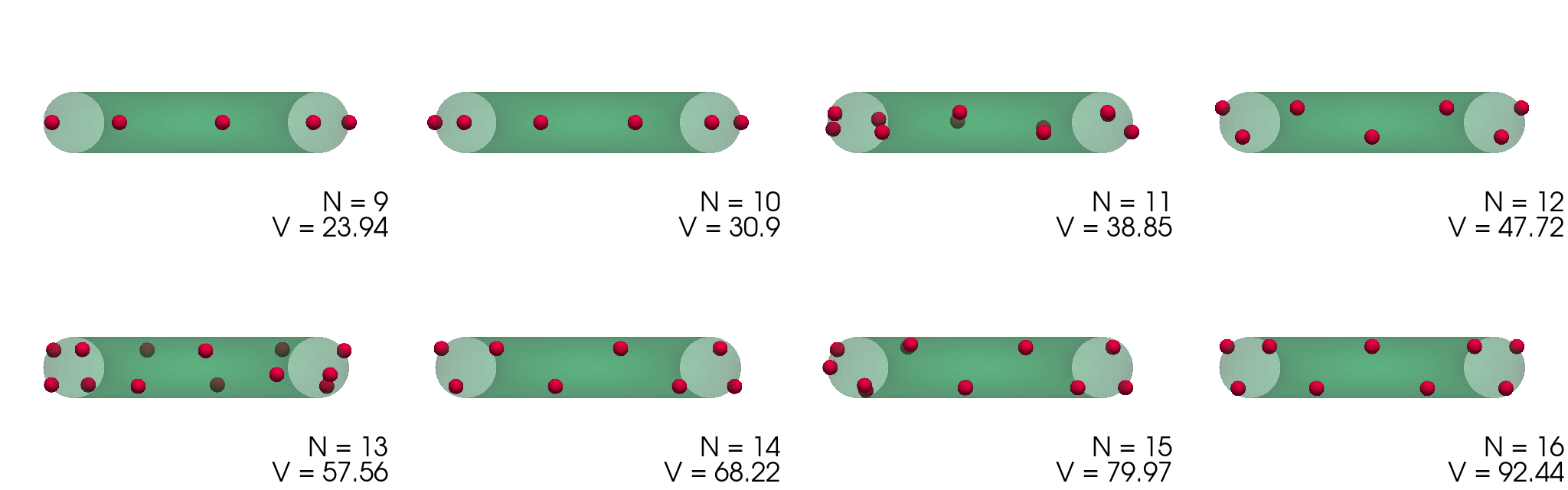
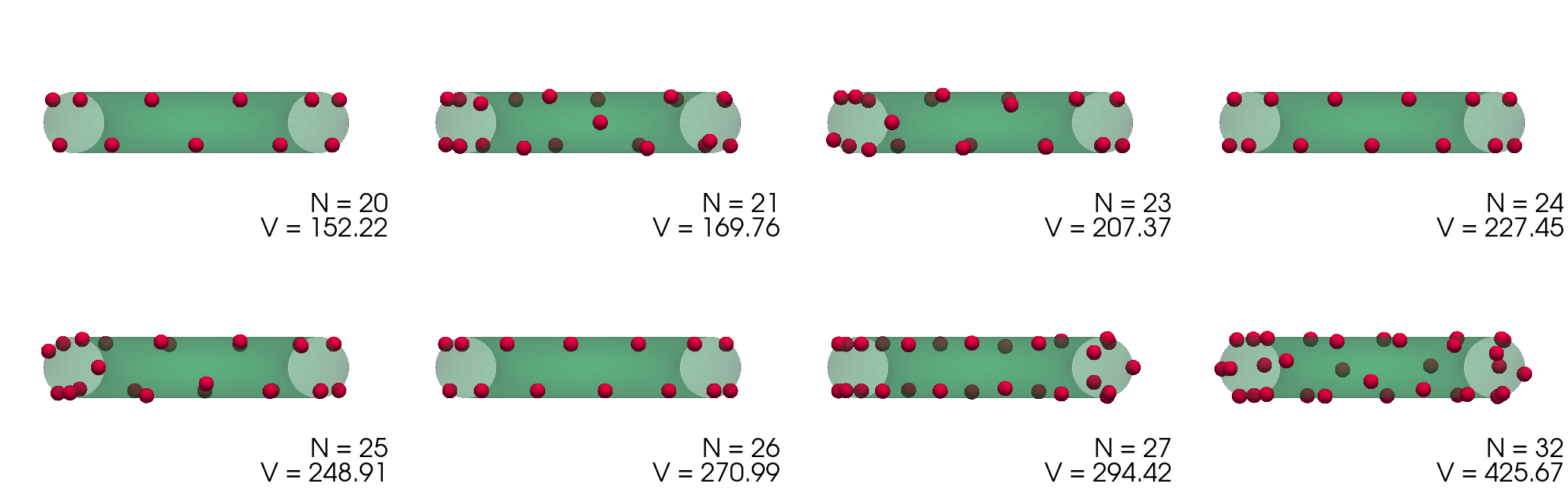
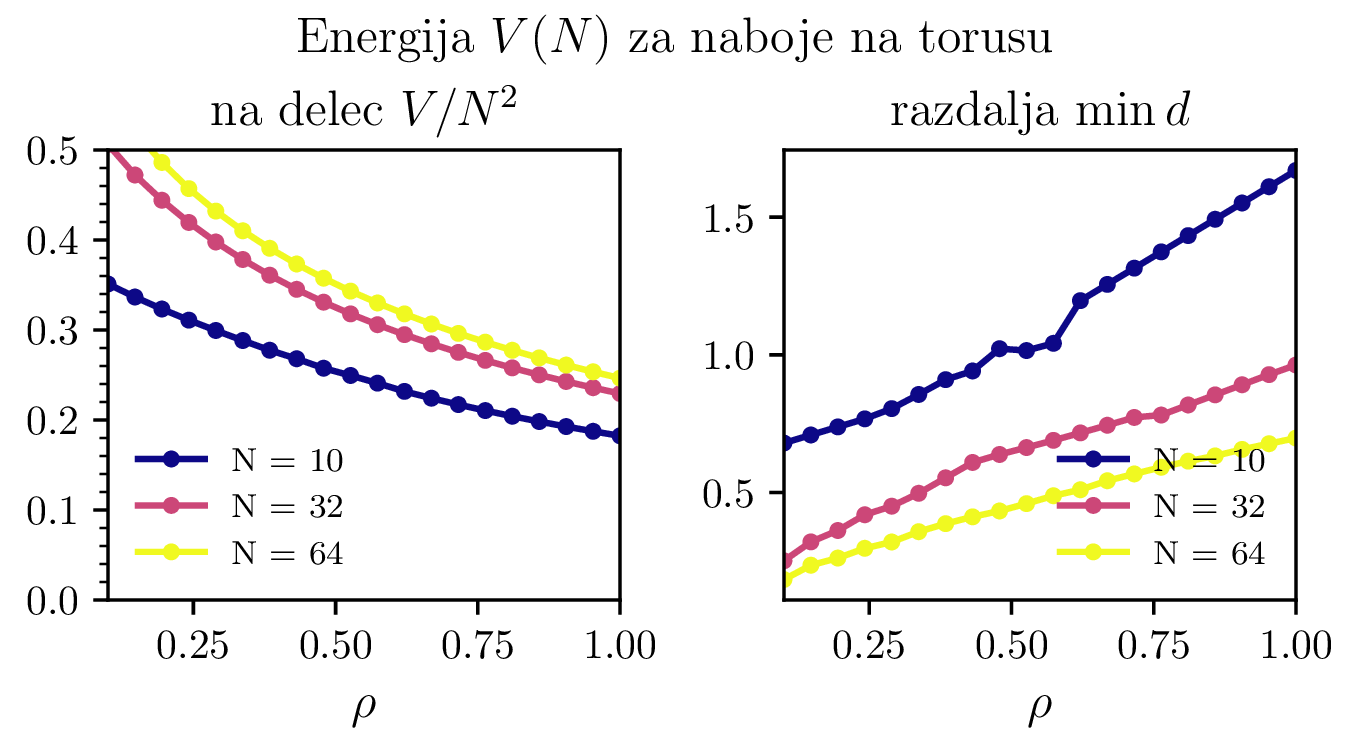
Podoben problem minimizacije potencialne energije (1) bomo rešili še za naboje na površini torusa, spet parametriziranega z \((\vartheta, \phi)\) kot \[\mathbf{r} = \begin{pmatrix} (1 + \rho \cos\vartheta) \cos\phi & (1 + \rho \cos\vartheta) \sin\phi & \rho \sin\vartheta \end{pmatrix}.\] Dobljene konfiguracije za \(\rho = 1\) torus narišemo na slikah 3 in 4. Za \(N <= 10\) so naboji razporejeni po zunanjem obodu torusa z radijem \(1 + \rho\). Za večje \(N\) so razporeditve presenetljivo nesimetrične (slika 4), izjema je le razporeditev za \(N = 24\), ki je edina zares simetrična glede na preslikavo čez veliko os torusa.
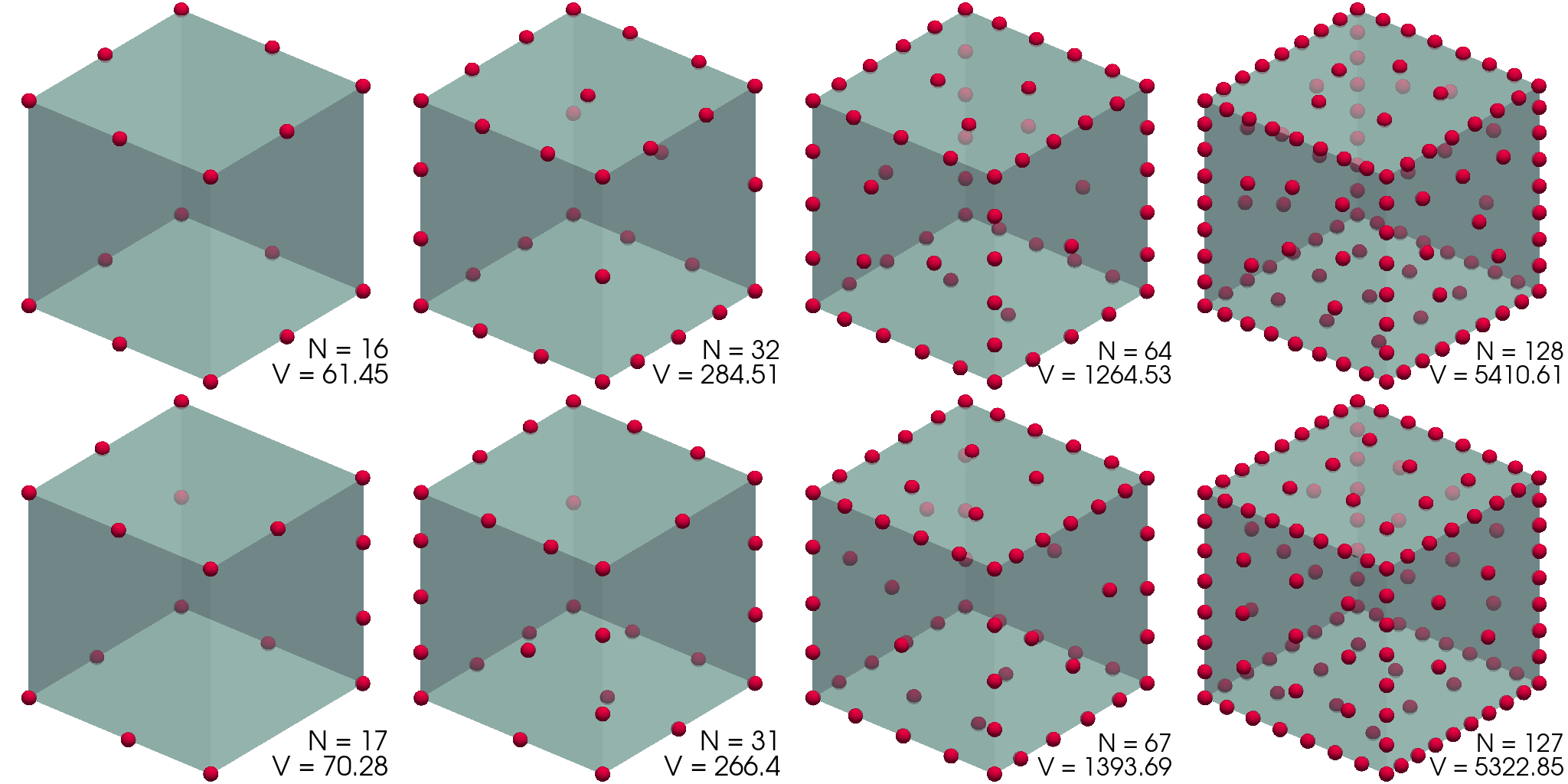
Naboji na površini kocke
Še ena površina, za katero je precej lepo reševati problem porazdelitve nabojev, je kocka. Namesto dejanske kocke bomo vzeli t. i. super-sfero \[x^{2p} + y^{2p} + z^{2p} = 1, \quad p \in \mathbb{N},\] pri čemer izberemo \(p\) dovolj velik, da je kocka "ostra". Konkretno izberemo \(p = 200\). Površino prav tako kot pri krogli parametriziramo s kotoma \((\theta, \phi)\), le da za radij velja \[r(\vartheta, \phi) = \left( \frac{1}{ \cos^{2p}\vartheta + (\cos\phi \sin\vartheta)^{2p} + (\sin\phi \sin\vartheta)^{2p} } \right)^\frac{1}{2p}.\] Dobljene porazdelitve nabojev narišemo na slikah 7 in 8.
Izogibanje lokalnim maksimumom
V namen izogibanja lokalnim maksimumom sem uporabil zelo preprost postopek. Prvo sem metodo zagnal za neke (tipično naključne začetne pogoje), nato pa sem optimizacijo pognal še 10-krat, z začetnimi parametri, ki sem jih dobil kot vsoto dobljenega prvega maksimuma in \(\sigma = 1\) ali \(\sigma = 5\) Gaussovskega šuma. Tako sem se izognil nekaterim lokalnim maksimumom, a da sem jim zares ušel, ne morem trditi.
Energije in zvezna limita
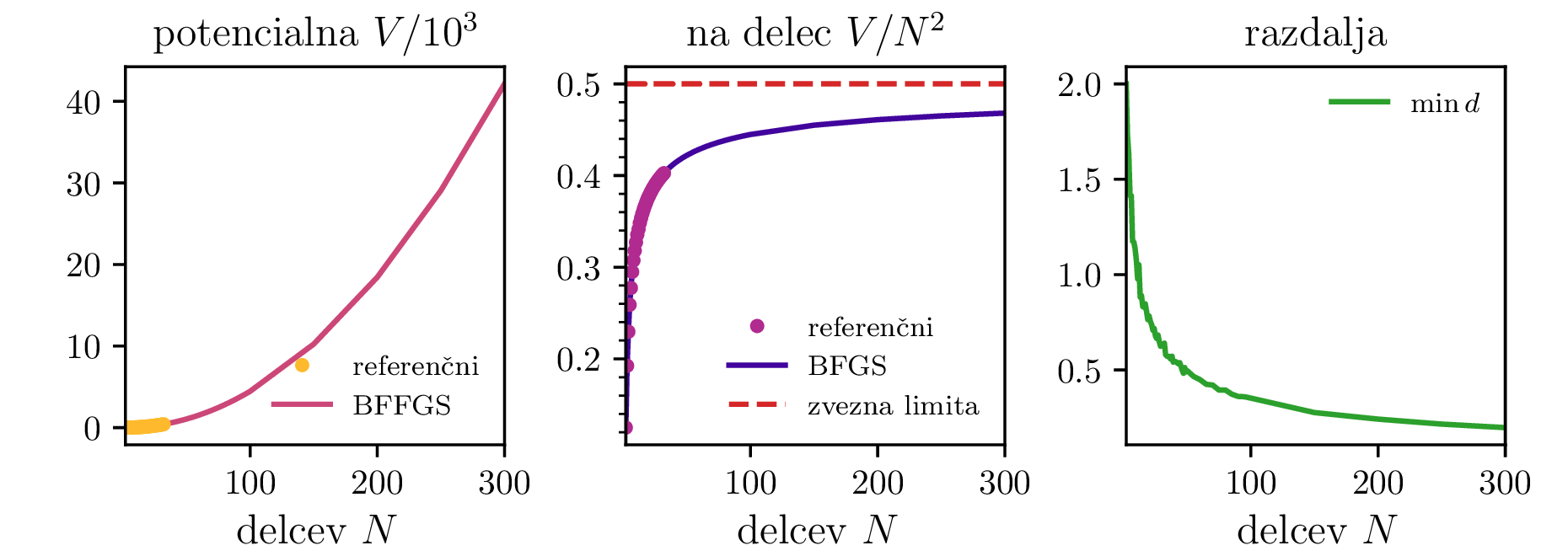
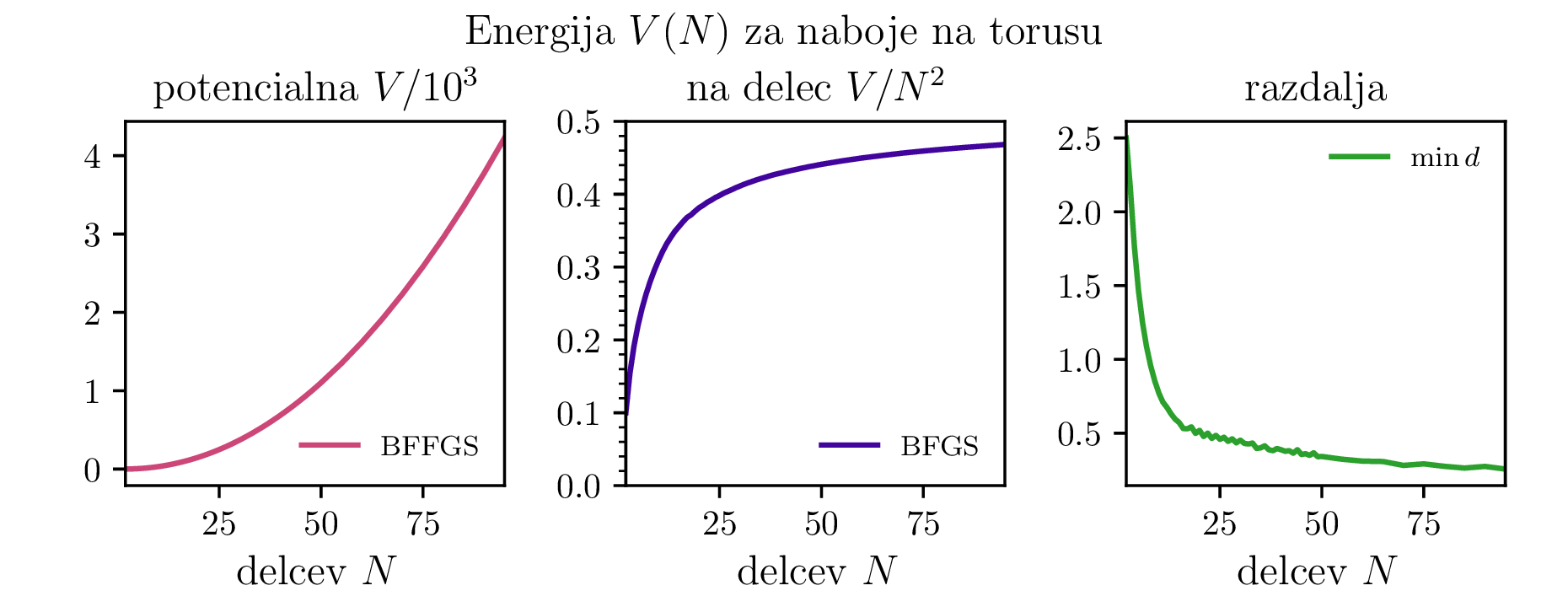
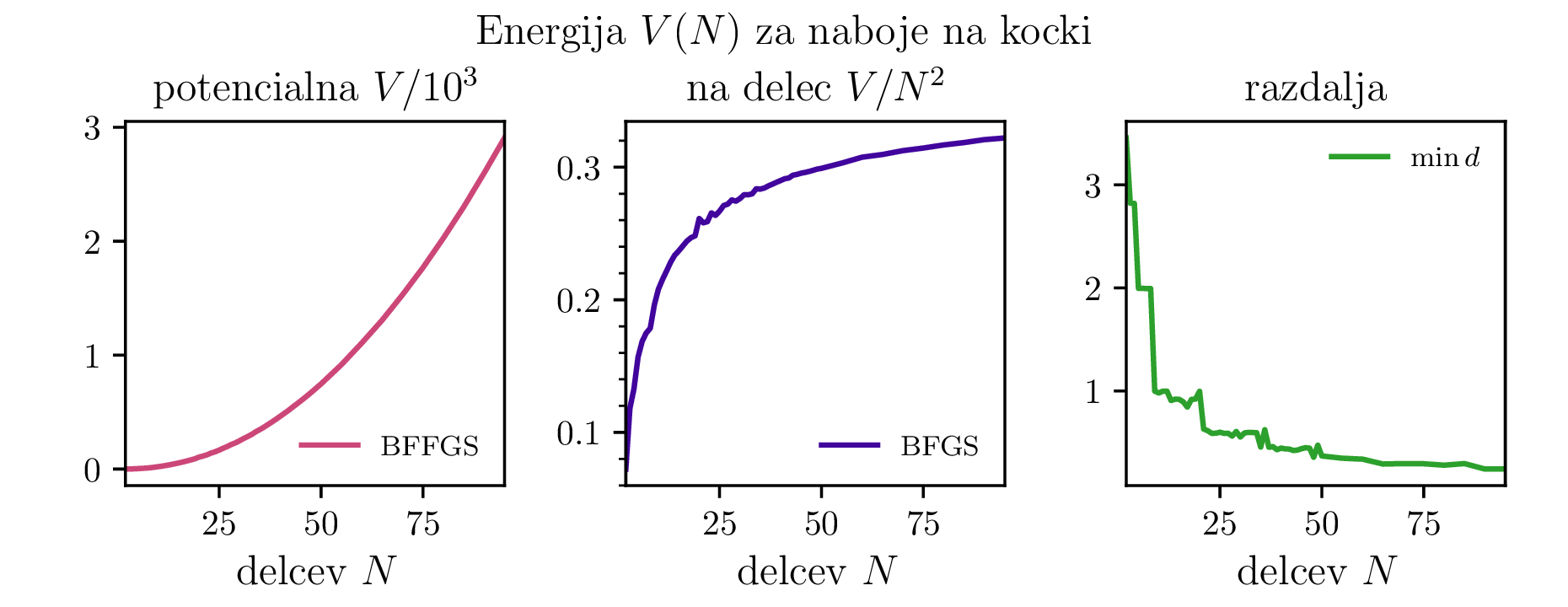
Preverimo lahko tudi zvezno limito Thomsonovega problema. Komulativna interakcija vsakega izmed delčkov \(\mathrm{d}S\) električno nabite krogle \(R = 1\) z ostalimi naboji te krogle (površinska gostota \(\sigma = \frac{N}{4\pi}\)) je \[V = 4\pi \sigma \int_{4\pi} \frac{\sigma\,\mathrm{d}S(\mathbf{r})}{|\mathbf{r} - \mathbf{r_0}|} = \frac{N^2}{2},\] kar ustreza tudi našemu diskretnemu problemu, ko gre \(N \to \infty\) (glej sredinsko sliko 2).
Tudi potencialna energija konfiguracij na torusu (slika 5) ima podobno obliko. Iizgleda, da se približuje \(0.5\). Za kocko (slika 9) pa je vrednost stalno nekoliko nižja in se vizualno približuje neko vrednosti med \(3\) in \(4\).
Natančnost in časovna zahtevnost
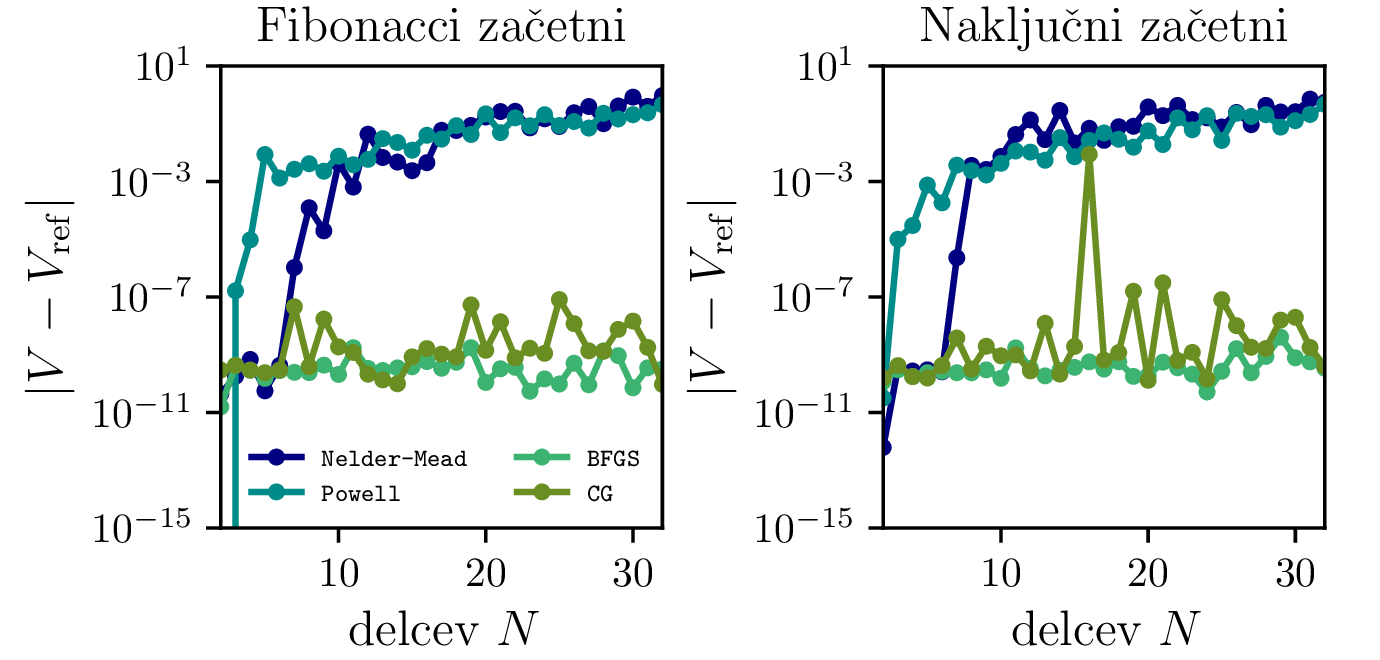
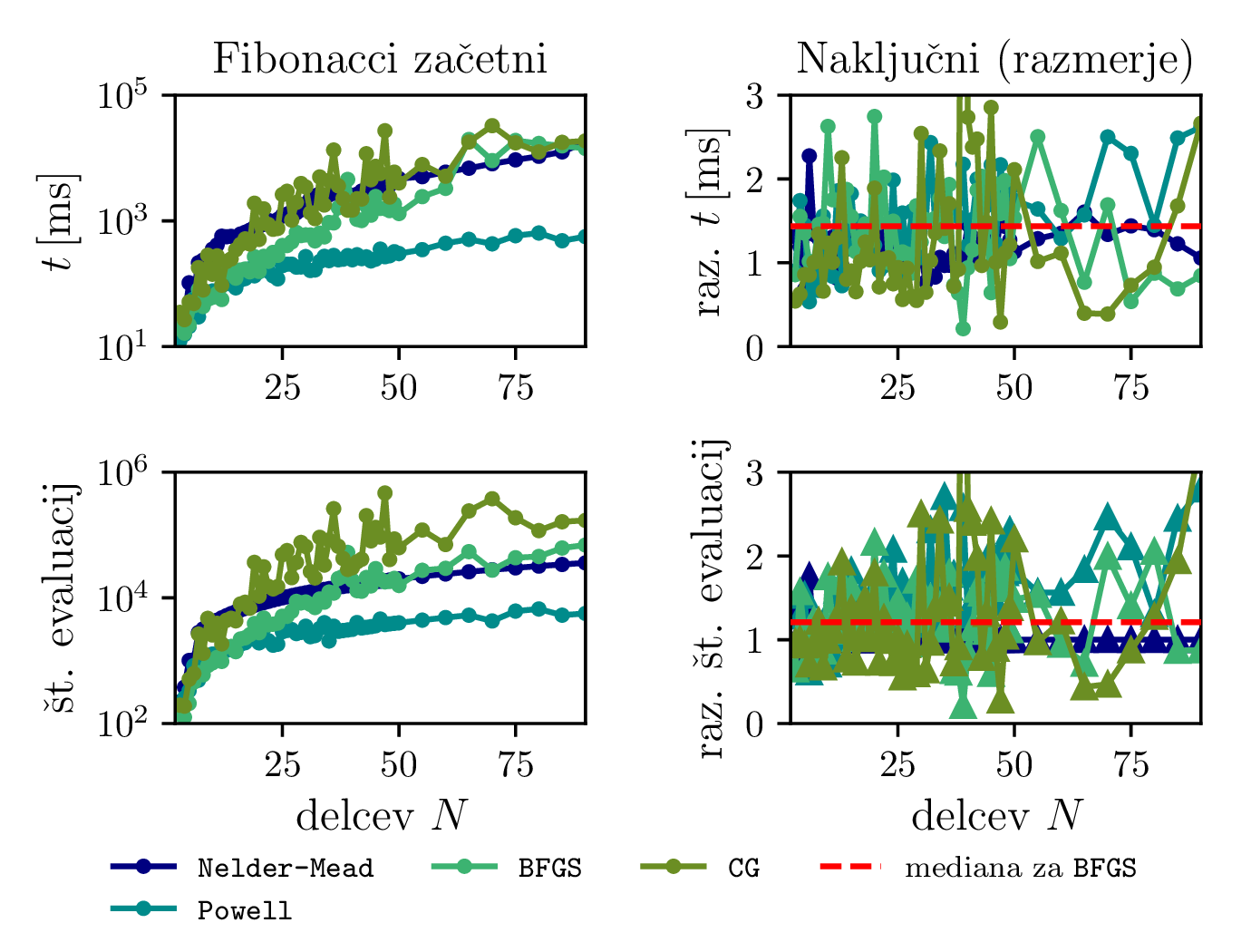
Natančnost algoritma lahko ocenimo s tem, da preverimo odstopanja izračunanih minimalnih potencialnih energij od referenčnih vrednosti iz [1]. Na sliki 10 vidimo odstopanja za prvih 32 nabojev za različne metode in dva različna začetna pogoja. Vidimo, da sta metodi BFGS in CG znatno boljši od drugih dveh. Nelder-Mead (simplex) in Powellova metoda v SciPy vmesniku vrneta opozorilo:
Warning: Maximum number of function evalutaions has been exceeded.
Tudi če za faktor 10 povečamo število dovoljenih vrednotenj funkcije (sorazmerno z \(N\)), to izboljša rezultat Nelder-Mead in Powellove metode le za par naslednjih \(N\). Ti dve metodi torej zelo hitro rastete v časovni zahtevnosti v odvisnosti od \(N\). Časovno zahtevnost si bolj natančno pogledamo na slikah 12, 13. Vidimo, da sta metodi BFGS in CG precej hitrejši od Nelder-Mead (simplex) metode in Powellove metode. Za večje \(N\) (npr. \(N > 200\)) pa se nam splača problem pognati tudi na GPU enoti (glej sliko 13).
Različni začetni pogoji
Poskusimo tudi, ali lahko pravilna izbira začetnih pogojev pospeši reševanje problema. Primerjali bomo začetno naključno in Fibonaccijevo razporeditev \[(\vartheta, \phi) = \left( \frac{i}{\varphi}, \frac{i + 1/2}{N} \right), i = 0, 1, \dots, N,\] pri čemer je \(\phi \approx 1.61803\). Na sliki 11 vidimo, da je potencialna energija \(V\) stalno manjša pri Fiboneccijevi kot pri naključni razporeditvi. Zato bi torej pričakovali, da je tak začetni pogoj bližje rešitvi Thomsonovega problema in bo kot tak hitreje konvergiral k dejanski rešitvi. To preverimo z dejanskim vrednotenjem na sliki 12, kjer narišemo čase izvajanja in števila evaluacij \(V\) v odvisnosti od števila delcev. Od metod se najboljše izkažeta metodi BFGS in CG, primerjava med začetnimi pogoji pa pokaže (slika 12 desno), da so naključni začetni pogoji na primeru BFGS metode v mediani okoli \(44\%\) slabši od Fiboneccijevih v času konvergence in \(21\%\) slabši v števila evaluacij \(V\). Torej se nam v večini primerov splača vzeti Fiboneccijeve začetne pogoje.
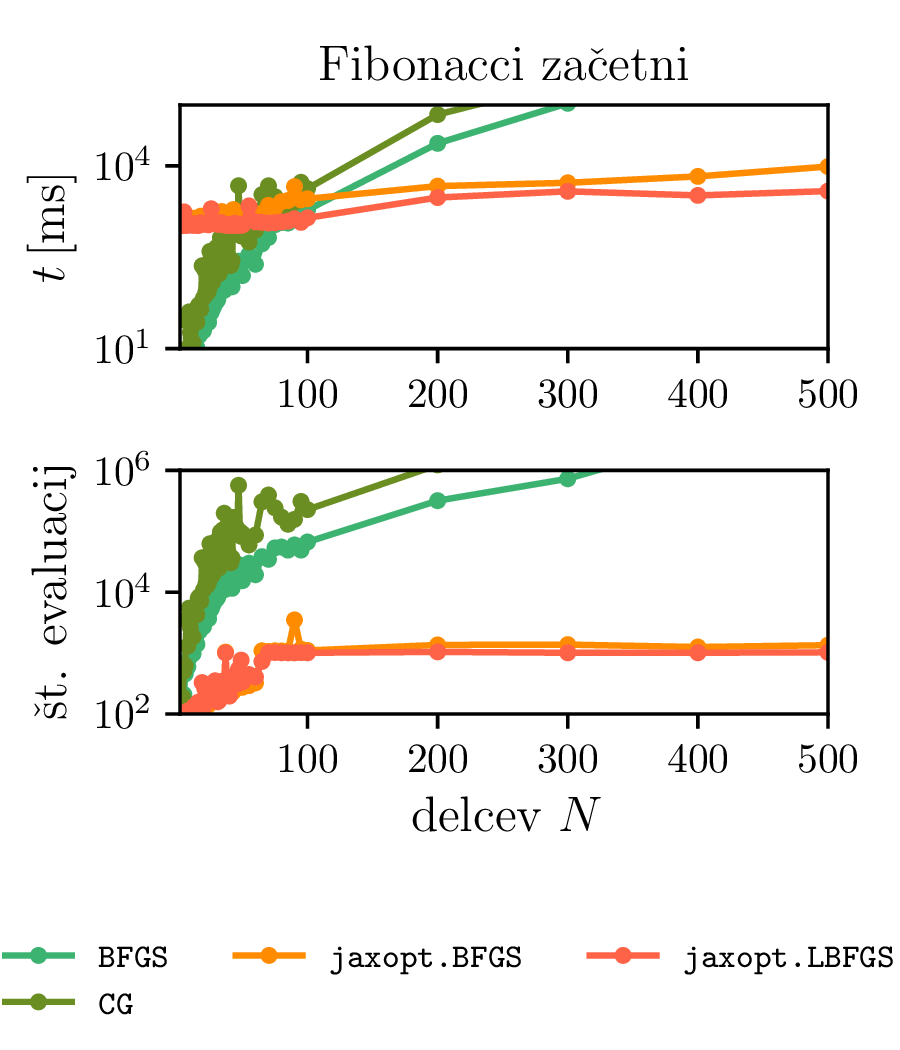
jaxopt metode iz
istoimenske knjižnice. Te metodi se izvajata na GPU enoto in odraža veliko manj izrazito rast kot CPU metode
iz SciPy. Za \(N = 200\) in več sta precej hitrejši od metod, ki se izvajata
na CPU. Hkrati pa sta manj primerni za majhne \(N\), kjer še vedno vidimo
overhead priprave in prenašanja podatkov na GPU.
Optimalna vožnja skozi semaforje
Zdaj bomo kot minimizacijski problem rešili še 1. nalogo optimalne vožnje do semaforja1. Prvo potek \(w(\tau)\) diskretiziramo na mreži \[w_i = w(\tau_i), \quad \tau_i = \frac{1}{N_\tau}, \frac{2}{N_\tau}, \dots, \frac{N_\tau}{N_\tau}.\] Pravzaprav ne potrebujemo povsem splošnih metod minimizacije, temveč je dovolj njegov posebni primer, t. i. kvadratično programiranje, kjer je kriterij za minimizacijo oblike \[c = \mathbf{q}^T \mathbf{x} + \mathbf{x}^T H \mathbf{x},\] pri čemer je matrika \(H\) neka pozitivno semi-definitna matrika, t. j. kvadratna forma \(\mathbf{x}^T H \mathbf{x}\) predstavlja nek minimum, ne maksimuma ali sedla. Za optimizacijo kumulativnega kvadrata pospeška prvo določimo pospeške preko končnih diferenc (forward diferenca 1. reda). V matričnem zapisu \begin{equation}\dot{\mathbf{w}} = \begin{bmatrix} \dot{w}_1 \\ \dot{w}_2 \\ \dot{w}_3 \\ \vdots \end{bmatrix} \approx N \begin{bmatrix} w_2 - w_1 \\ w_3 - w_2 \\ w_4 - w_3 \\ \vdots \end{bmatrix} = N \begin{bmatrix} -1 & 1 \\ 0 & -1 & 1 \\ & 0 & \ddots & \ddots \\ & & \ddots & \ddots & 1 \\ & & & 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ \vdots \end{bmatrix} = D_1 \mathbf{w} \label{eq:matrix}\end{equation} Če želimo čim manjši kumulativni kvadrat pospeška, je optimizacijski kriterij \begin{equation}c = \dot{\mathbf{w}}^T \dot{\mathbf{w}} \approx (D_1 \mathbf{w})^T D_1 \mathbf{w} = \mathbf{v}^T H_1 \mathbf{w}, \label{eq:c-qp}\end{equation} pri čemer je Hessova matrika iz same definicije pozitivno semi-pozitivna \[H_1 = D_1^T D_1 = N^2 \begin{bmatrix} 1 & -1 \\ -1 & 2 & -1 \\ & -1 & 2 & -1 \\ & & -1 & \ddots & \ddots \\ & & & \ddots & \ddots & -1 \\ & & & & -1 & 1 \\ \end{bmatrix},\] in je precej podobna matriki končnih diferenc za \(-\ddot{w}\), razen v zgornjem levem in spodnjem desnem kotu. Pri optimizaciji zahtevamo, da semafor prevozimo ob času \(\tau = 1\), kar ustreza linearni vezi \begin{equation}1 = \int_0^1 w \,\mathrm{d}\tau \approx \frac{1}{N} \left( w_1 + w_2 + \dots + w_N \right). \label{eq:vez-0}\end{equation} To vez bi lahko upoštevali tako, kot je predlagano v navodilu naloge, npr. s strelsko metodo na rešitvah za nek \(\lambda\). Sam sem izbral preprostejši način upoštevanja te vezi. Sicer se gre za to, da lahko na podlagi vezi (4) eno spremenljivko kar odstranimo iz funkcijske oblike optimizacijskega kriterija \[c(w_1, w_2, \dots, w_{N_\tau}) = c(w_2, \dots, w_{N_\tau}),\] saj lahko preko vezi izrazimo \(w_1 = f(w_2, w_3, \dots)\). Ugotovil sem, da je v implementaciji zares dovolj, da take odvečne prostostne le "skrijemo" iz funkcijske odvisnosti kriterija, ne tudi odstranimo iz prostora parametrov \(\mathbf{w}\), v katerem iščemo optimalno rešitev. V kodi to izgleda kot:
def regularize(w_vals, *args):
num, w0, w1, _, _, _, fixed_w1, _ = args
w_vals[0] = w0
if fixed_w1:
w_vals[num - 1] = w1
w_vals[1] = (1 - 1 / num * (w_vals[0] + np.sum(w_vals[2:]))) * num
return w_vals
def cost_semafor_nonlinear(w_vals, *args):
_, _, _, w_max, β, edge_type, _, FD1 = args
w_vals = regularize(w_vals, *args)
dot_w = FD1 @ w_valsPrimerjava med splošno in kvadratično optimizacijo
Za optimizacijski kriterij komulativnega pospeška (3) lahko brez težave uporabimo splošne metode nelinearne optimizacije, kot smo to počeli za Thomsonov problem. A kot bomo videli imajo metode za kvadratično optimizacijo mnogo prednosti.
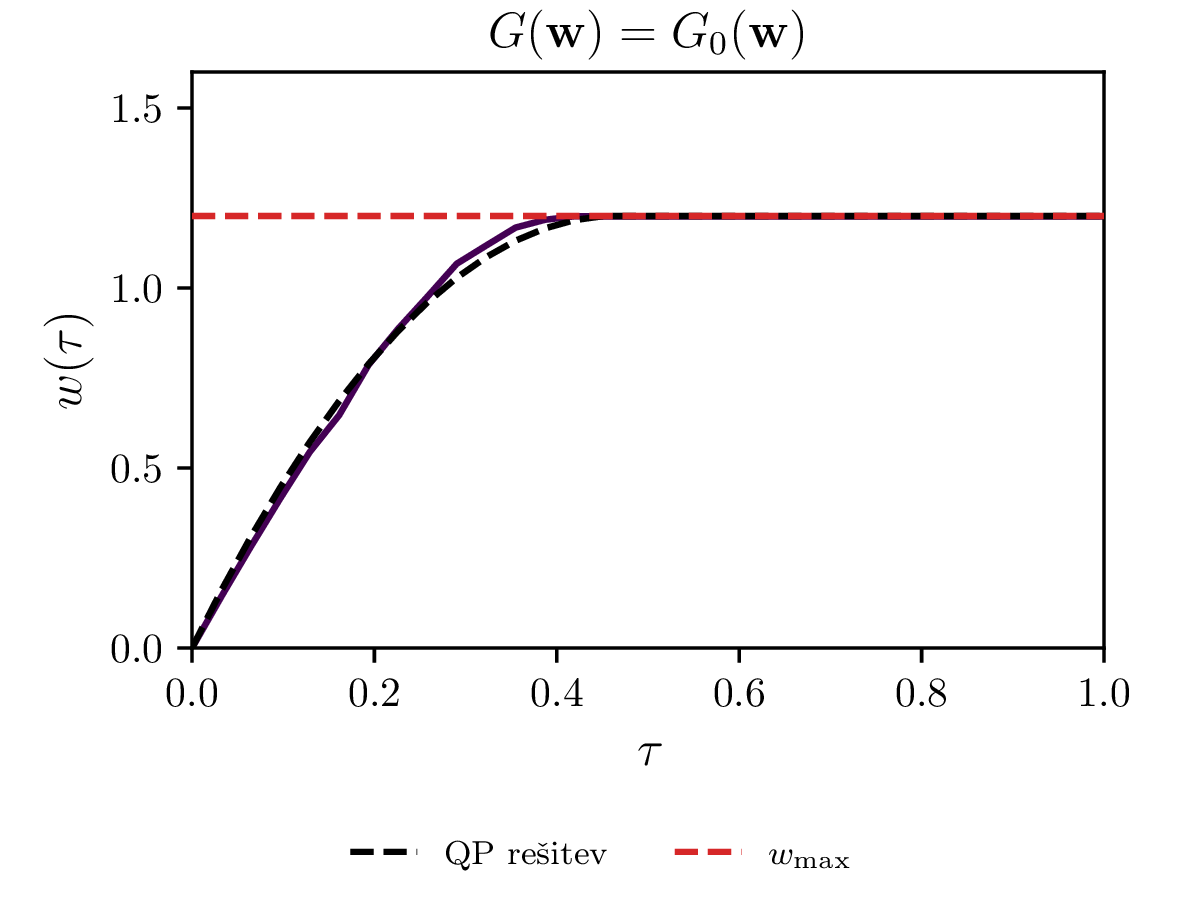
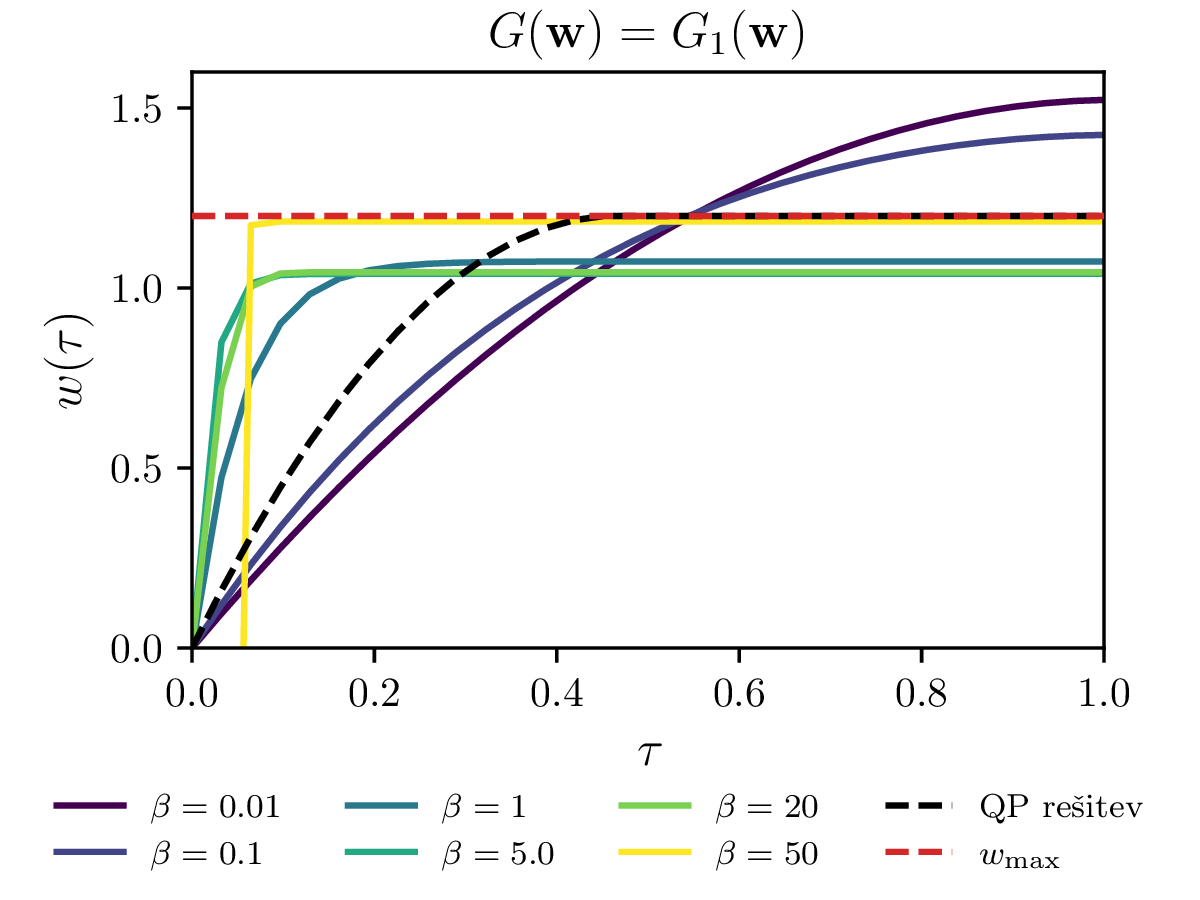
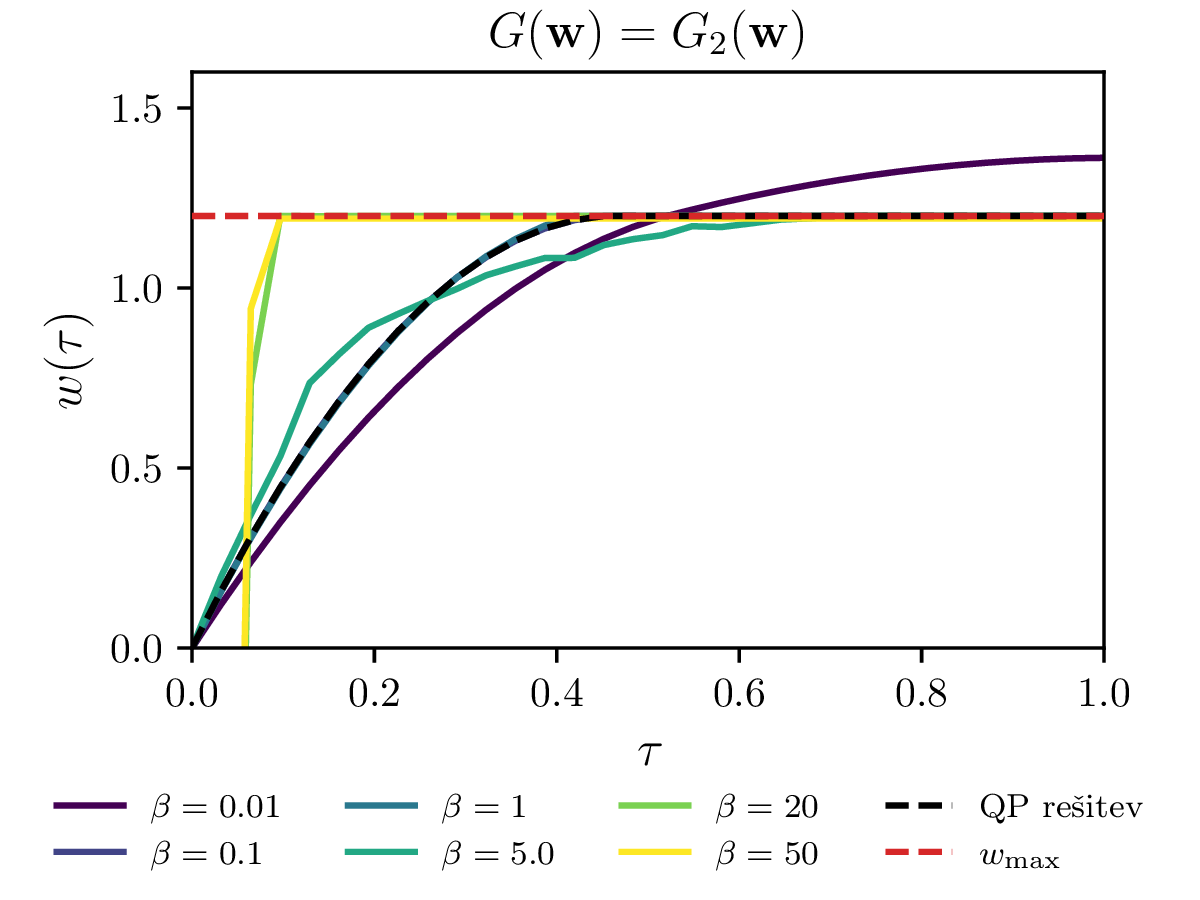
Za kvadratično optimizacijo oz. t. i. kvadratično programiranje z lahkoto izrazimo vezi kot je npr. omejitev maksimalne hitrosti. Splošne nelinearne optimizacijske metode pa tipično delujejo v režimu brez vezi. Vezi moramo tedaj dodati našemu kriteriju kot \[c^{(z vezmi)}(\mathbf{w}) = c(\mathbf{w}) + G(\mathbf{w}),\] pri čemer je \(G(\mathbf{w})\) funkcija, ki zavzema veliko (idealizirano neomejeno) vrednost izven dovoljenega območja, ki ga določa vez. Če bi torej za metodo kvadratičnega programiranja zahtevali po elementih \[\mathbf{w} \le w_\text{max},\] moramo za splošne nelinearne metode dodati kriteriju nek \(G\). Poskusili in primerjali bomo \(G\) funkcije oblik \begin{equation}\begin{aligned} G_0(\mathbf{w}) &= \sum_i 10^6 \cdot \theta(w_i - w_\text{max}), \label{eq:g0} \\ G_1(\mathbf{w}) &= \sum_i e^{\beta (w_i - w_\text{max})}, \label{eq:g1} \\ G_2(\mathbf{w}) &= \sum_i \mathop{\text{max}} \left ( 0, e^{\beta (w_i - w_\text{max}) - 1} \right), \label{eq:g2} \end{aligned}\end{equation} pri čemer je \(\theta(x)\) Heaviside koračna funkcija. Te funkcije primerjamo na sliki 14, kjer vidimo, da se lahko obnašajo precej patološko. Še najlepše se obnaša \(G = G_2\) za \(\beta = 1\), saj kar sovpada za QP rešitvijo.
Poleg tega, da za kvadratno programiranje ne potrebujemo izbirati oblike funkcije \(G\), je metoda tudi dosti hitrejša. Na sliki 15 vidimo, da so QP metode hitrejše kar za velikostni razred do dva, hkrati pa sem v lastnih eksperimentih spoznal, da so QP metode tudi dosti robustnejše.
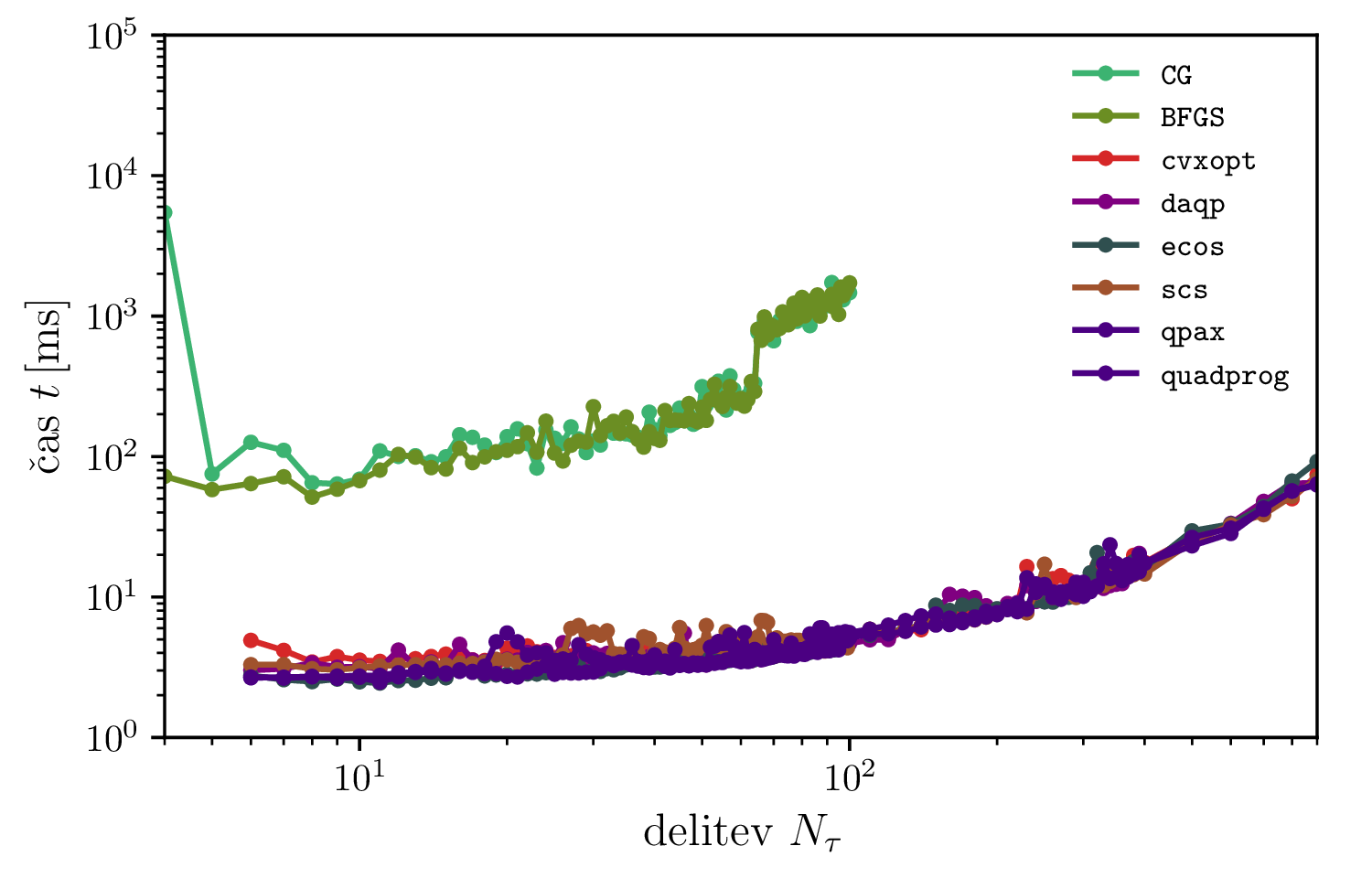
BFGS in CG) ter algoritme kvadratičnega programiranja
(cvxopt, daqp, ecos, scs, qpax,
quadprog). Kvadratično programiranje za tak tip problema omogoča mnogo hitrejše reševanje.
Več omejitev za vožnjo skozi semafor
Ko problem optimalne vožnje rešujemo v diskretizirani obliki, imamo na voljo precej bogat nabor možnih omejitev za naše rešitve. Te pridejo v problem v direktno v obliki vezi, npr. \(\mathbf{w} \le w_\text{max}\), ali pa odstopanje od meje te vezi dodamo našemu minimizacijskemu kriteriju v obliki \(G(\mathbf{w})\) člena, ki kaznuje rešitve izven dovoljenega območja. Kar v obliki seznama bom navedel vse takšne omejitve, ki sem jih implementiral za model optimalne vožnje. Ker sem se zaradi hitrosti lažje igral z QP metodo, bom opisal kako sem jih implementiral v tem kontekstu. Prevod za uporabo z nelinearnimi metodami je preprost in sledi zgledu za omejitev maksimalne hitrosti iz slike 14.
-
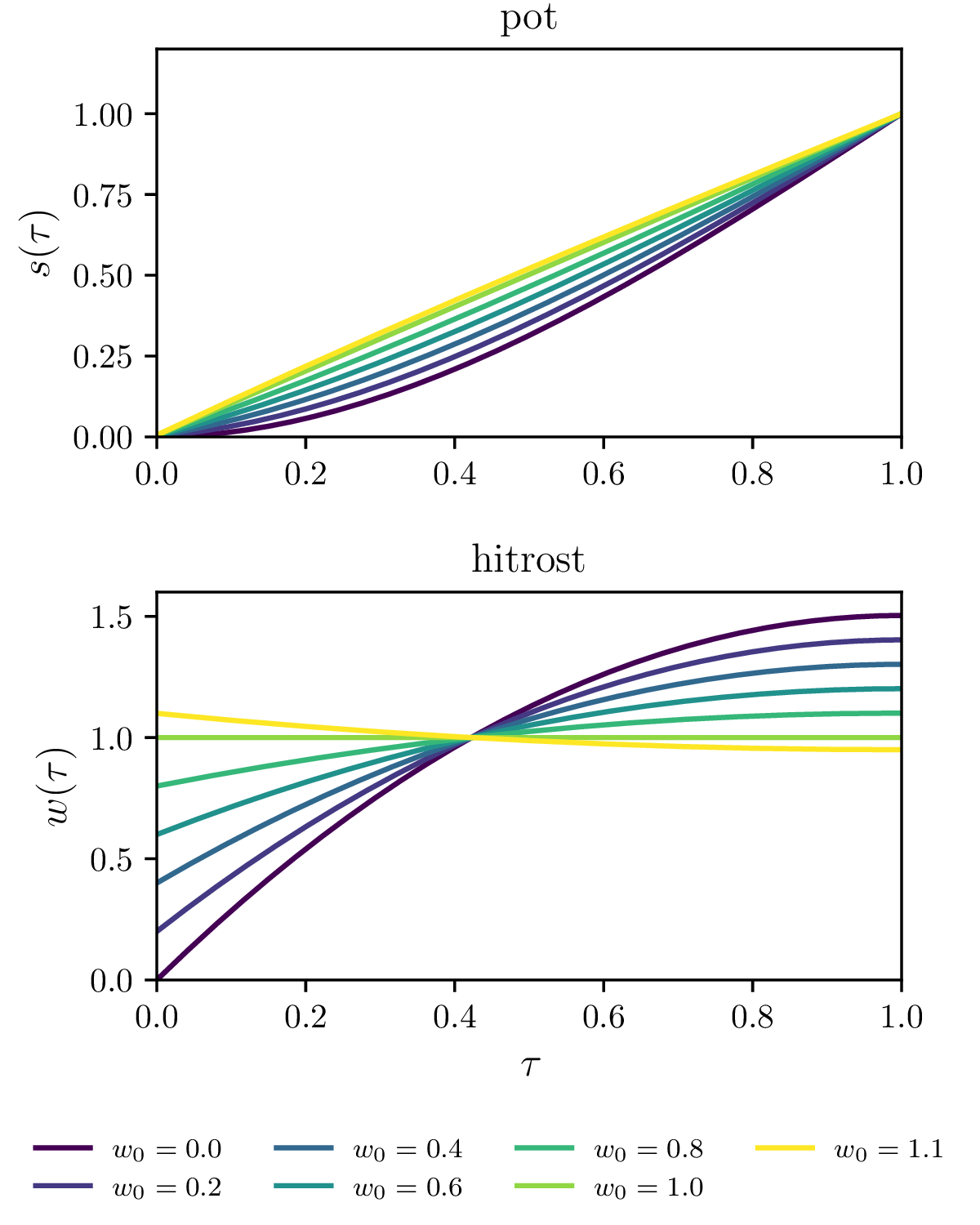
Fiksiranje začetne \(w_0\)
-
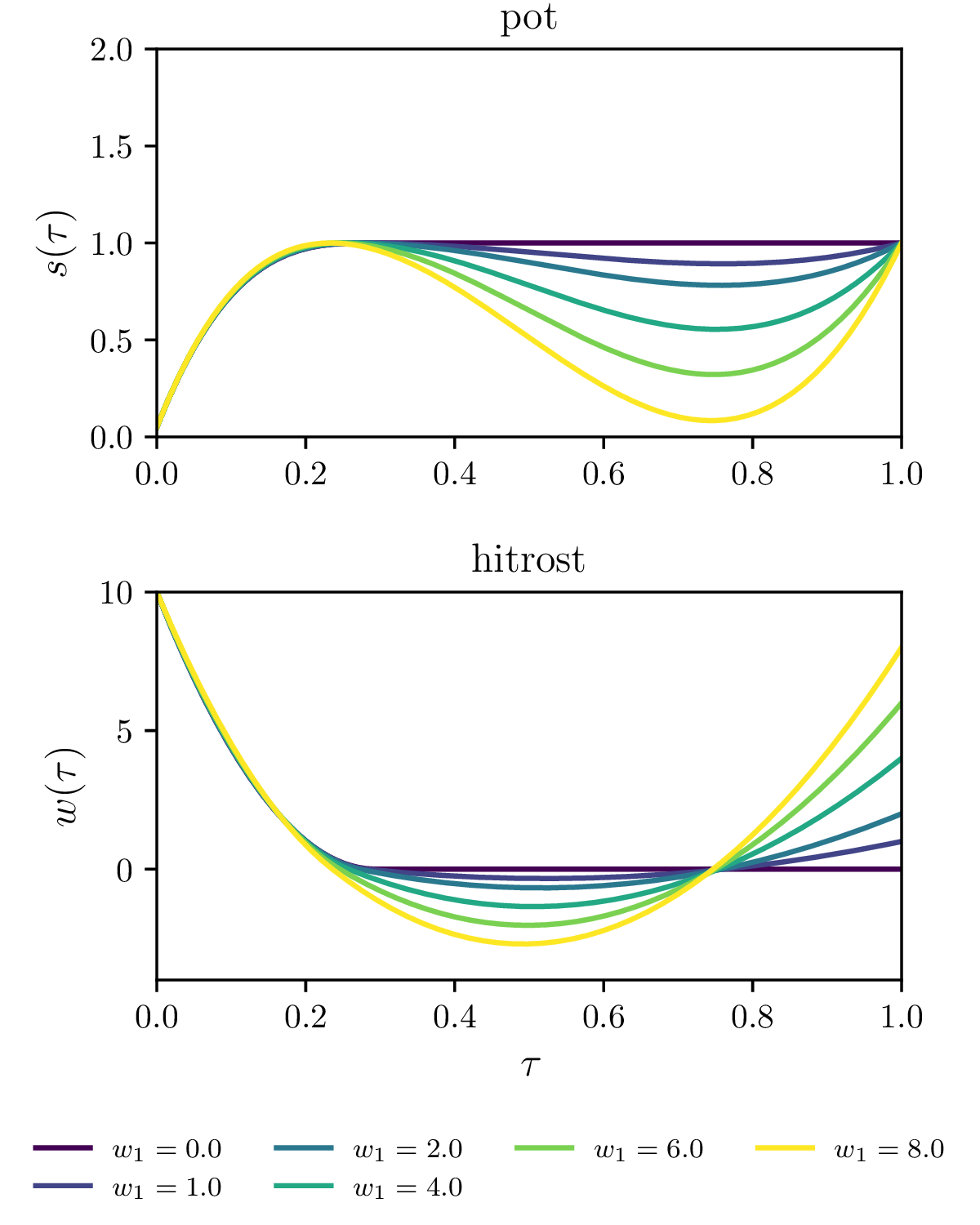
Fiksiranje končne \(w(1) = w_1\) hitrosti.
-
Vez opravljene poti \(s(1) = 1\) do semaforja (izraz (4)).
-
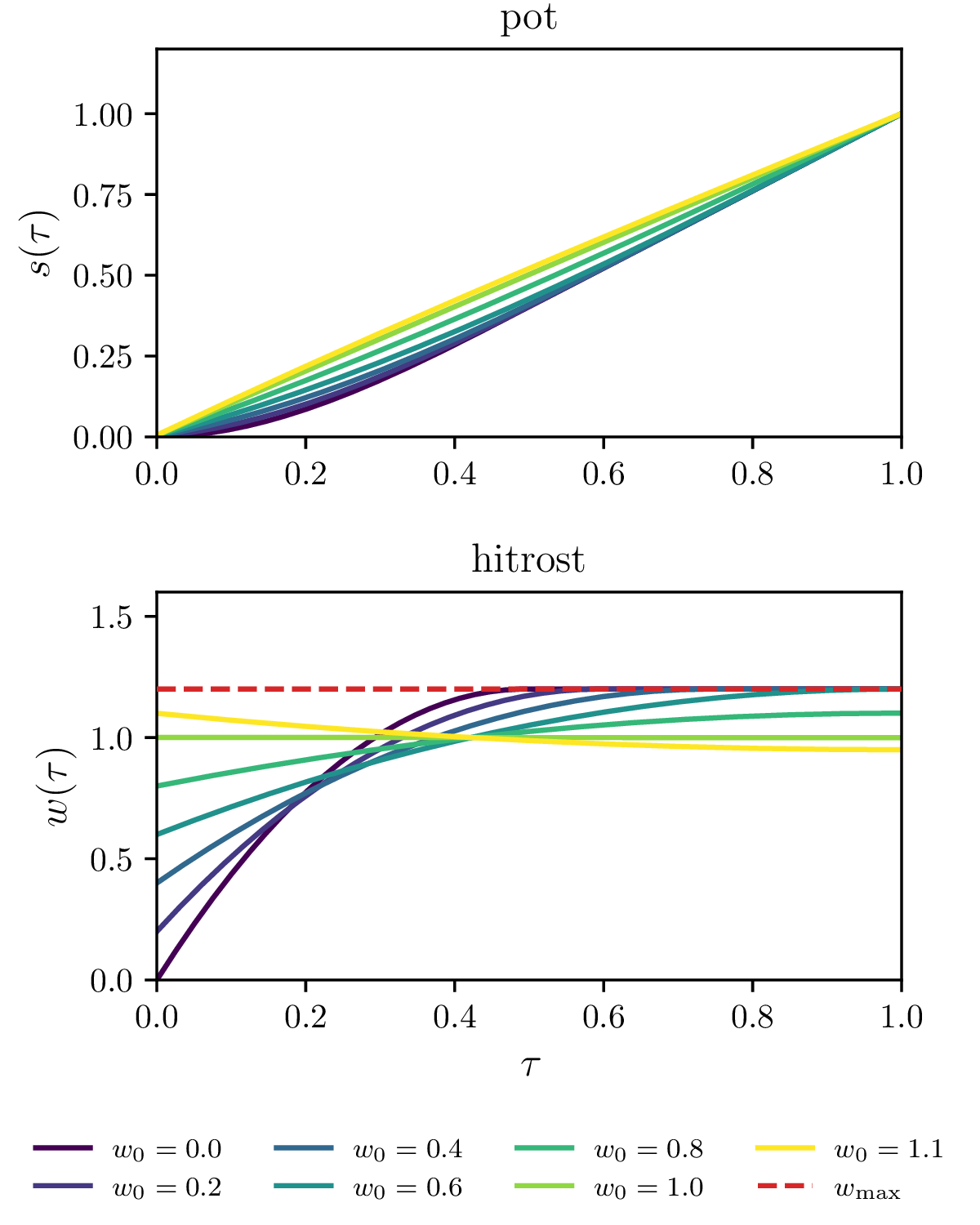
Omejitev maksimalne hitrosti \(\mathbf{w} \le w_\text{max}\) (glej sliko 16).
-
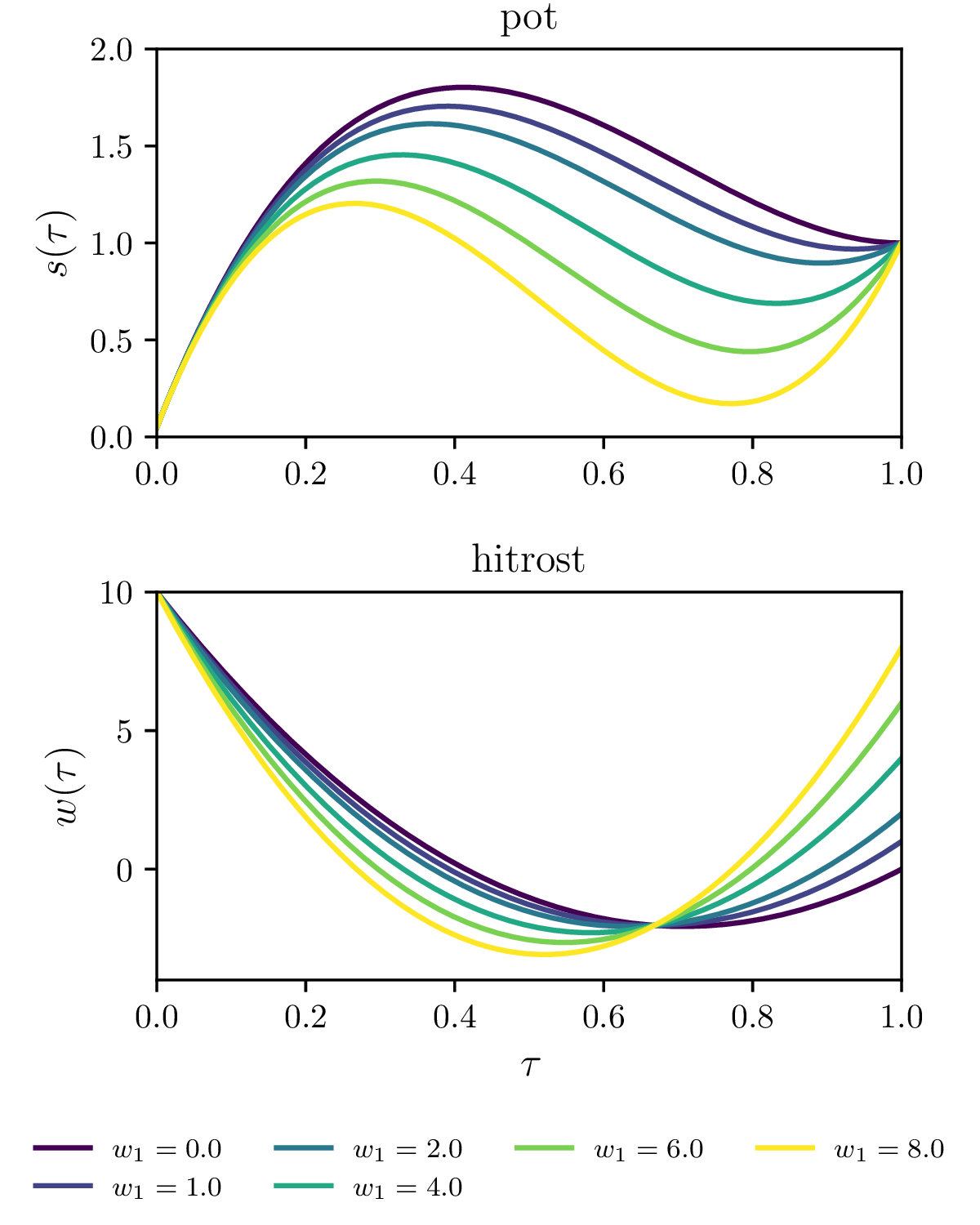
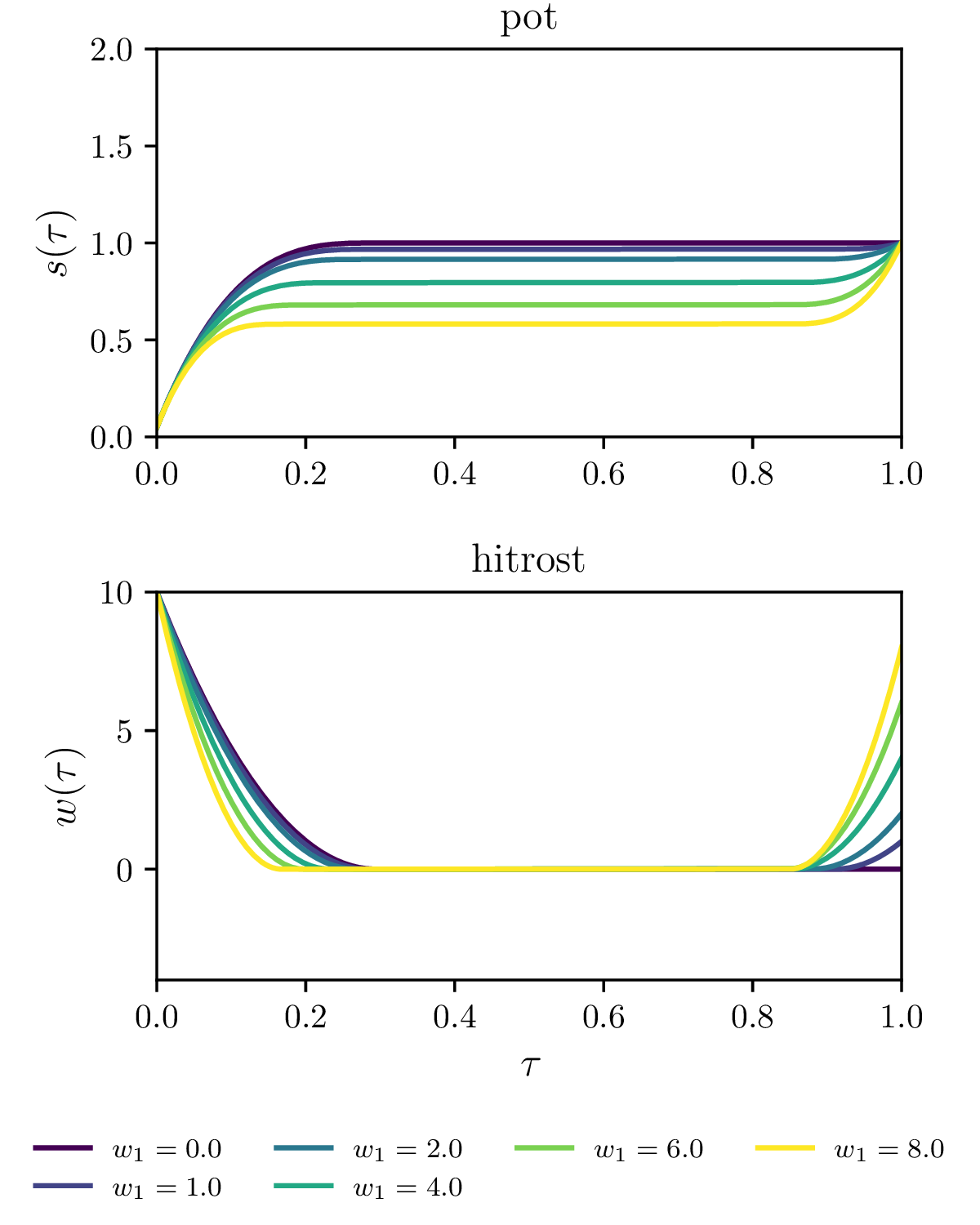
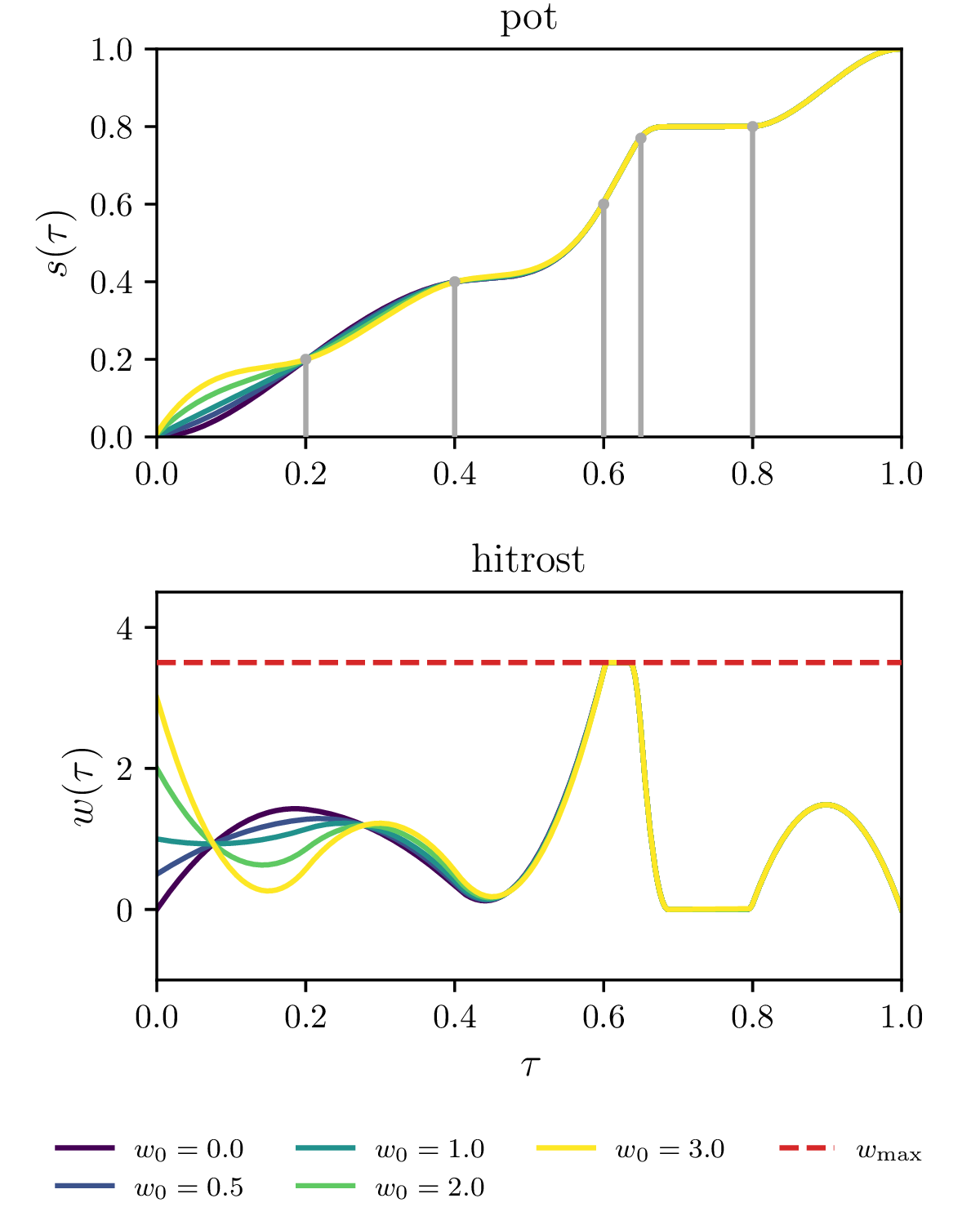
Prepoved negativnih hitrosti \(\mathbf{w} \ge 0\). To prepreči overshoot čez semafor, saj je pot potem monotona funkcija (tretja slika 17).
-
Manj stroga omejitev za preprečevanja overshoota čez semafor pred \(\tau = 1\), ki za vsak \(i = 1, 2, \dots, N\) zahteva \(\int_0^{\tau_i} w\,\mathrm{d}\tau \le 1\) (tretja slika 17).
-
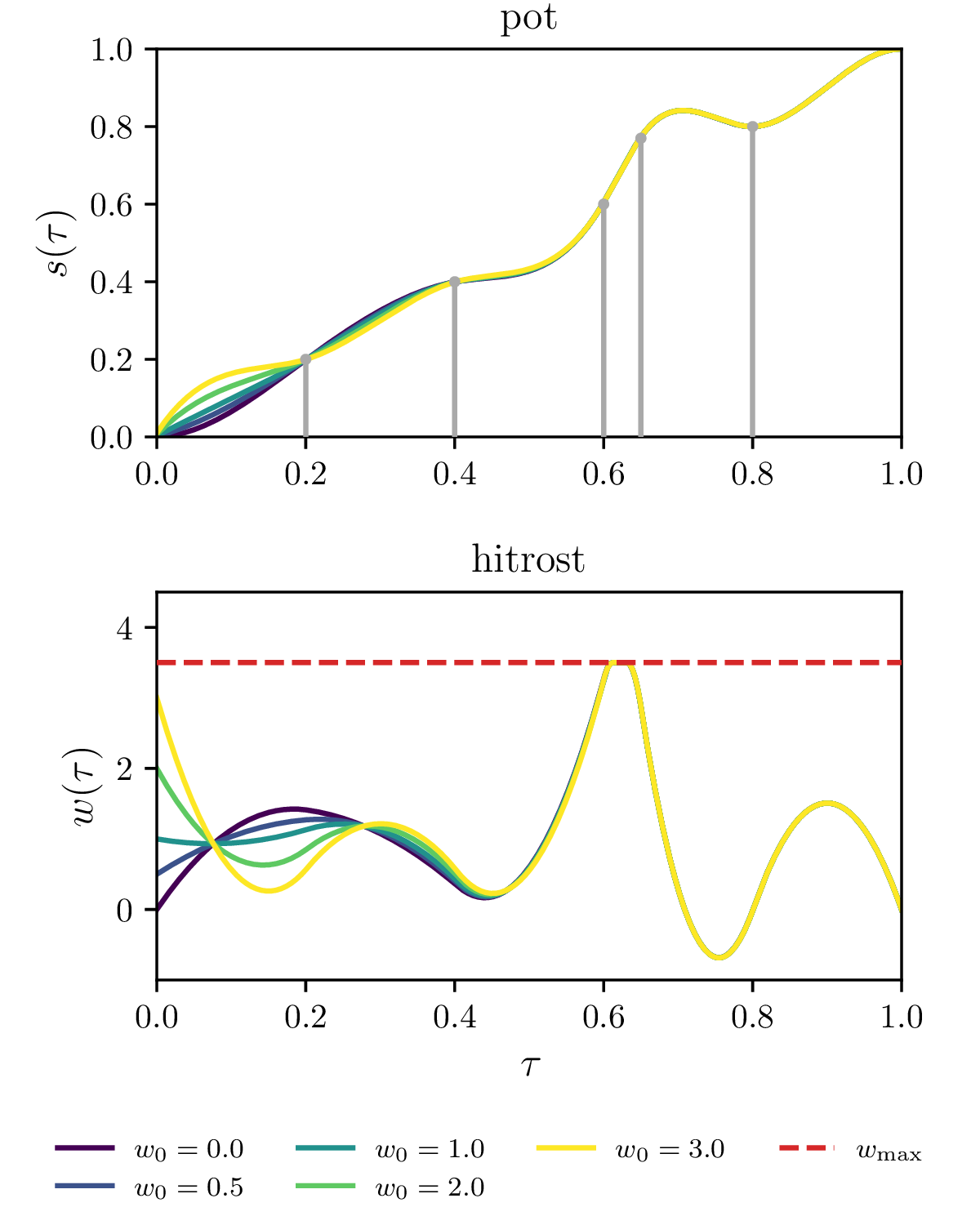
Poljubni semaforji, postavljeni za \(k = 1, 2, \dots, N_\text{sem}\), pri čemer \((\tau_k, s_k)\) določata položaj semaforja in čas prižiga semaforja. Za vsak semafor \((\tau_k, s_k)\) izberemo nek \(\tau_i\) iz osnovne diskretizacije, ki je najbližje \(\tau_k\), nato pa zahtevamo \(\int_0^{\tau_i \approx \tau_k} w\,\mathrm{d}\tau = s_k\). Na slikah 18 vidimo primer 5 semaforjev, postavljenih v nekem neenakomernem zaporedju.
-
Omejitev za preprečevanje overshoota za semaforje \((\tau_k, s_k)\). Gre se le za omejitev iz 6. točke, le ponovljeno za vsak končni čas \(\tau = \tau_k\), ne le \(\tau = 1\). To omejitev vidimo na primeru 5 semaforjev na tretji sliki 18.