Problem optimalne diete

Linearno programiranje na primeru problema optimalne diete + kvadratično programiranje za optimalno vožnjo

Navodila

Med tipične primere, ki jih lahko učinkovito rešimo z metodami linearnega programiranja, sodi sestavljanje diet za hujšanje, zdravljenje ali športne aktivnosti. Za dani nabor živil določamo njihove količine, pri čemer moramo zadostiti različnim omejitvam. Med drugim moramo zagotoviti priporočene dnevne odmerke mineralov, vitaminov in hranilnih snovi, omejiti pri vnos maščob, ogljikovih hidratov ter telesu škodljivih snovi, hkrati pa zagotoviti, da energijska vrednost ustreza zahtevam posameznika. Vnos vsake izmed hranilnih snovi je linearna funkcija količin živil in je natanko določena z njihovo sestavo. Od vrste diete pa je odvisno, katere parametre omejimo in katere minimiziramo. Datoteka tabela-zivil.dat vsebuje podatke o energijski vrednosti ter vsebnosti maščob, ogljikovih hidratov, proteinov, kalcija in železa v nekaj živilih, skupaj z okvirnimi podatki o njihovi ceni.

Rešitev

Sestava diete je povsem specificirana z masami vsakega izmed tipov hrane, ki jih uživamo. Imenujmo to za vektor \[\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \end{bmatrix} = \begin{bmatrix} m_\mathrm{jabolko} \\ m_\mathrm{pomfri} \\ m_\mathrm{govedina} \\ \vdots \end{bmatrix}.\] Za našo dieto imamo nekaj linearnih zahtev, npr. želimo, da dieta zagotovi zadosten vnos železa. To izrazimo kot linearno vez \begin{equation}\begin{aligned} m_{\mathrm{Fe}} &= w^\mathrm{Fe}_\mathrm{jabolko} m_\mathrm{jabolko} + w^\mathrm{Fe}_\mathrm{pomfri} m_\mathrm{pomfri} + w^\mathrm{Fe}_\mathrm{govedina} m_\mathrm{govedina} + \dots \nonumber \\ &\le 18\,\mathrm{mg}, \label{eq:vez} \end{aligned}\end{equation} pri čemer so \(w^\mathrm{Fe}\) specifične (na \(100\,\mathrm{g}\)) vsebnosti železa v tem konkretnem živilu (npr. \(1.94\,\mathrm{mg}/100\,\mathrm{g}\) za govedino). Take specifične vsebnosti \(w^i_j\) za hranilne snovi \(i\) in živila, ki jih vsebujejo \(j\), imamo podane v tabela-zivil.dat, ilustrirano pa z nekaj podatki v tabeli 1.

živilo	energija \([\mathrm{kcal}]\)	maščobe \([\mathrm{g}]\)	\(\mathrm{Fe}\,[\mathrm{mg}]\)
Jabolko	52	0.17	0.12
Pomfri	93	12	0.35
Govedina	254	20	1.94

Vez (1) lahko izrazimo tudi kot skalarni produkt \[\mathbf{w}_\mathrm{Fe}^T \mathbf{x} \le 18\,\mathrm{mg},\] pri čemer je \(\mathbf{w}_\mathrm{Fe}\) vektor vsebnosti železa za vsa popisana živila (torej stolpec tabele 1 pod \(\mathrm{Fe}\)). Pravzaprav specificiramo poljubno takih vezi, skupno pa to zapišemo v matrični obliki. Npr. če želimo omejiti železo in natrij kot \[m_\mathrm{Fe} \ge 18\,\mathrm{mg}, \qquad 500\,\mathrm{mg} \le m_\mathrm{Na} \le 2400\,\mathrm{mg},\] lahko vse to izrazimo ekvivalentno v matrični obliki¹ kot \[\begin{bmatrix} -\mathbf{w}_\mathrm{Fe}^T \\ -\mathbf{w}_\mathrm{}^T \\ \mathbf{w}_\mathrm{}^T \\ \end{bmatrix} \le \begin{bmatrix} -18\,\mathrm{mg} \\ -500\,\mathrm{mg} \\ 2400\,\mathrm{mg} \\ \end{bmatrix},\] pri čemer razumemo, da omejitev velja za vsak element vektorja posebej.

Dieta za hujšanje

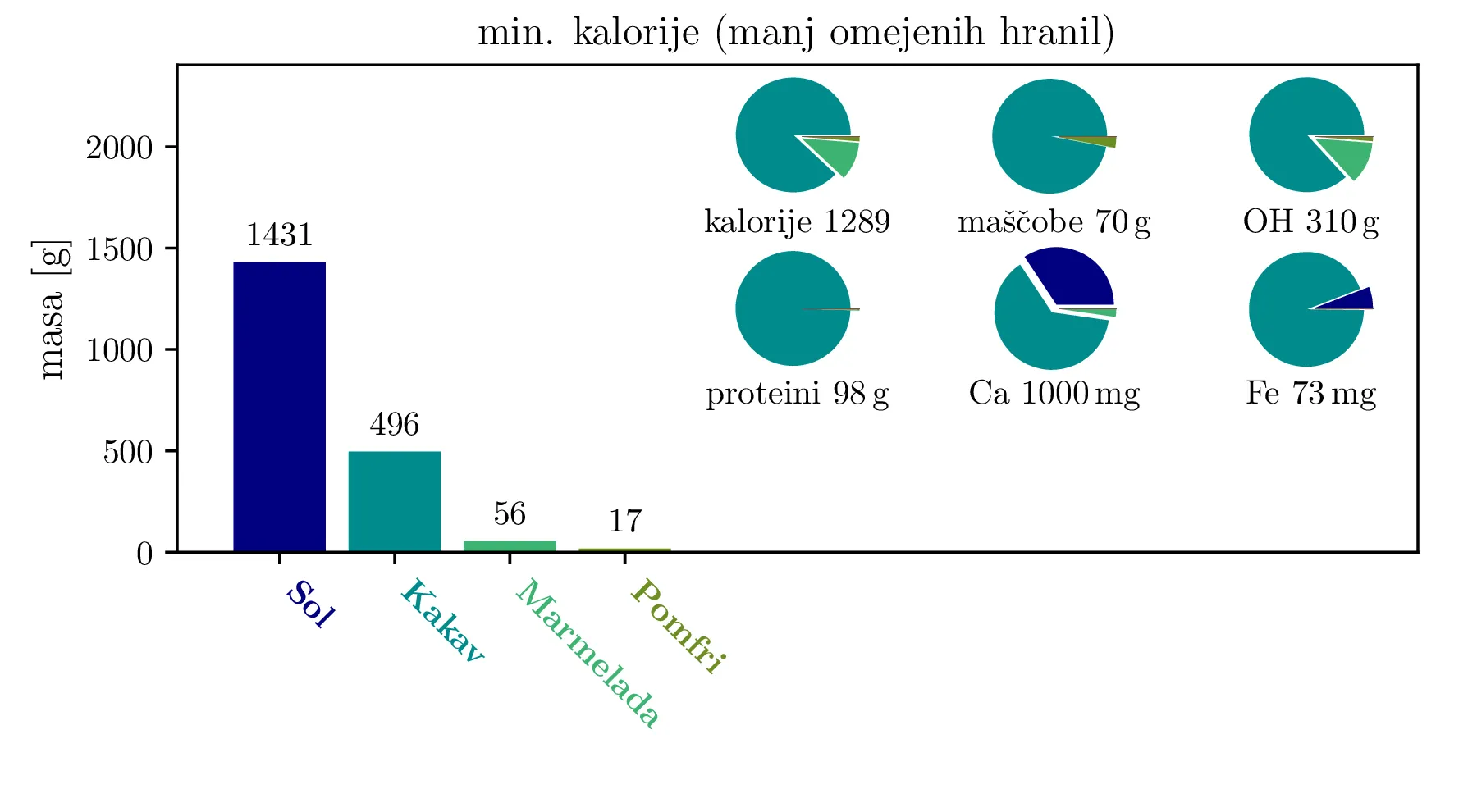
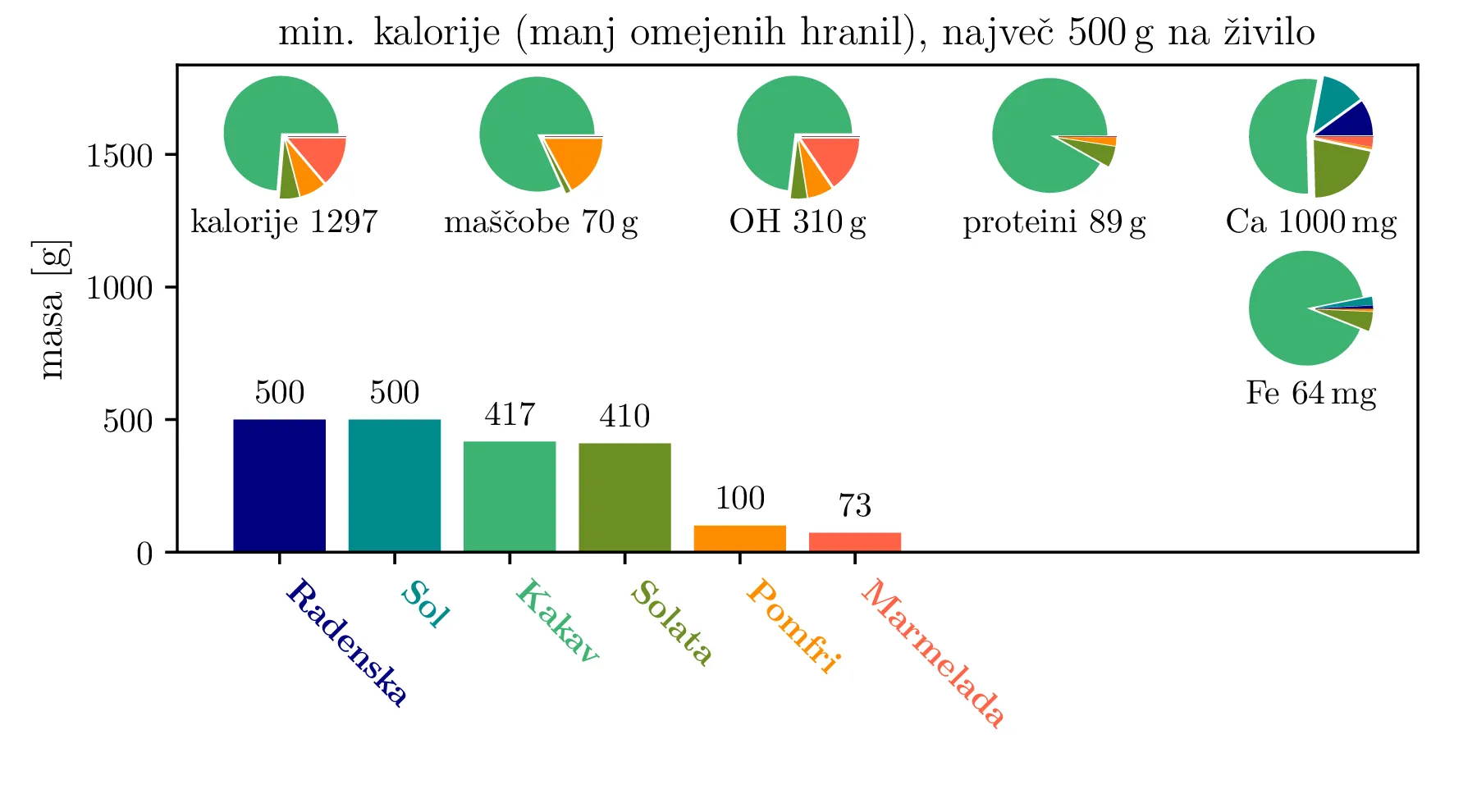
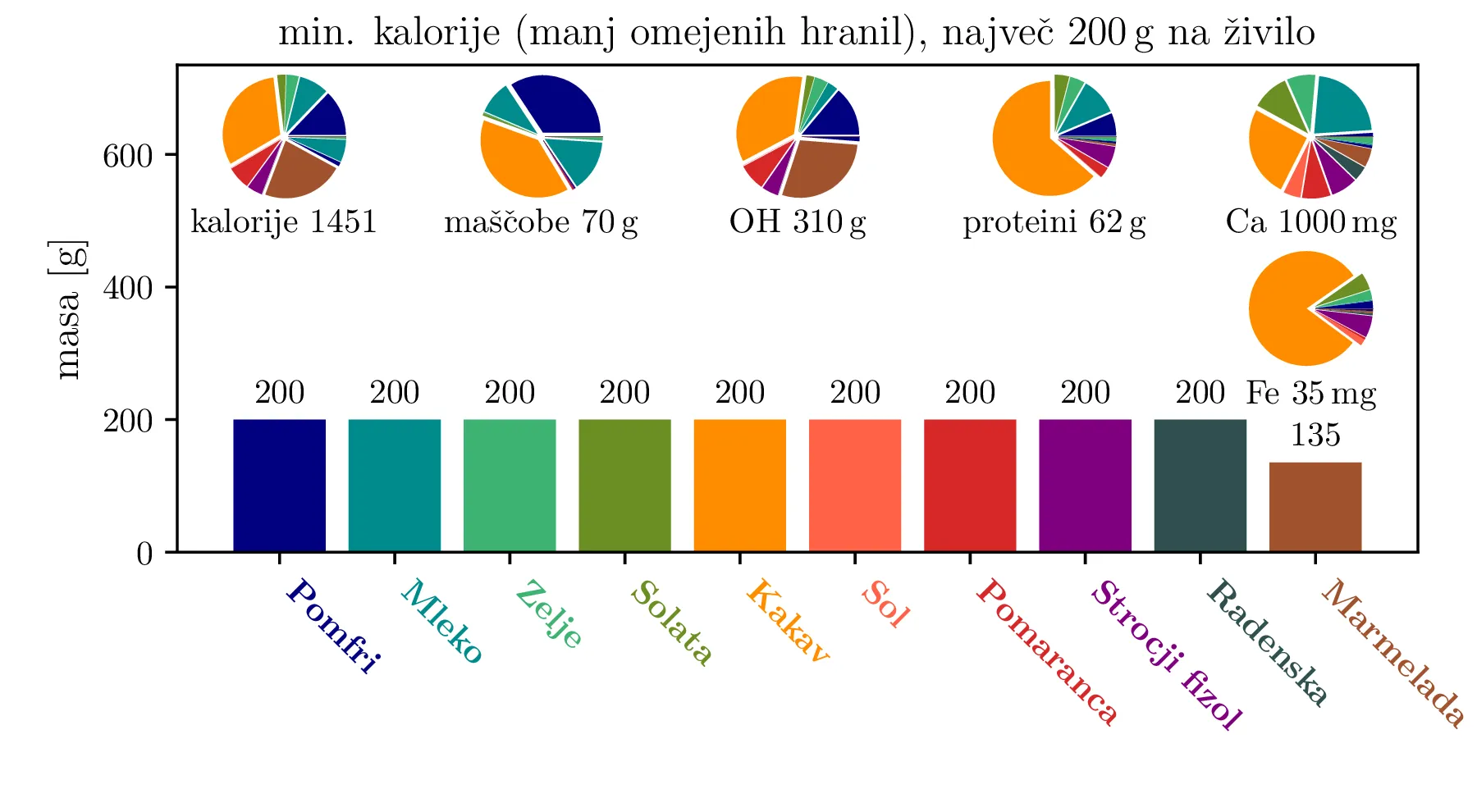
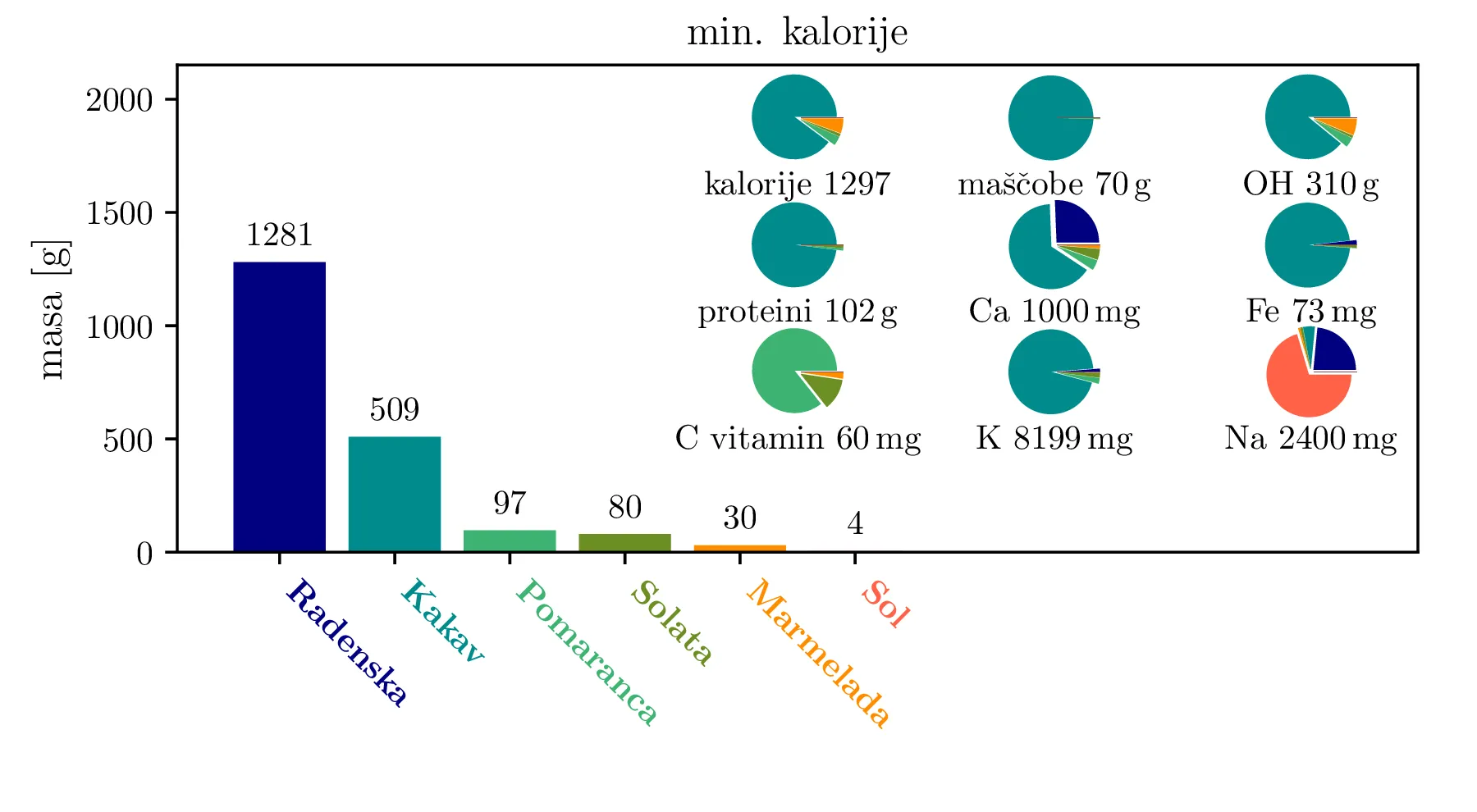
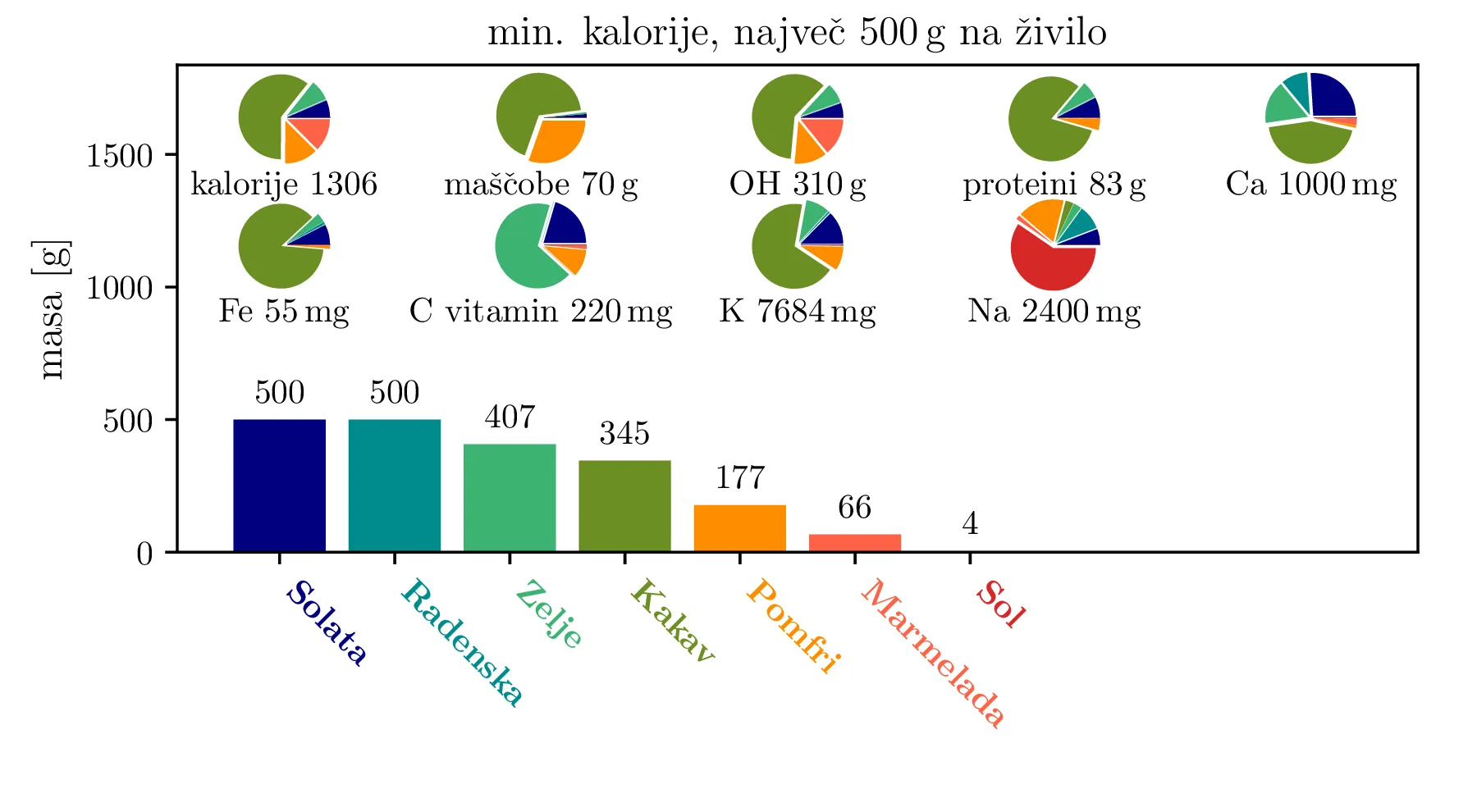
Prav tako kot vez (1), mora biti tudi funkcija, ki jo minimiziramo, linearna funkcija. Če recimo minimiziramo zaužite kalorije, je minimizacijska funkcija (ang. cost funkcija) oblike \begin{equation}\begin{aligned} c_{\mathrm{cal}} &= w^\mathrm{cal}_\mathrm{jabolko} m_\mathrm{jabolko} + w^\mathrm{cal}_\mathrm{pomfri} m_\mathrm{pomfri} + w^\mathrm{cal}_\mathrm{govedina} m_\mathrm{govedina} + \dots \nonumber \nonumber \\ &= \mathbf{w}_\mathrm{cal}^T \mathbf{x}, \label{eq:lin-model} \end{aligned}\end{equation} pri čemer je \(\mathbf{w}_\mathrm{cal}\) kar prvi stolpec tabele 1. Z minimizacijo zaužitih kalorij in omejitvami \begin{equation}\begin{aligned} m_\mathrm{maščobe} &\ge 70\,\mathrm{g} \nonumber \\ m_\mathrm{OH} &\ge 310\,\mathrm{g} \nonumber \\ m_\mathrm{proteini} &\ge 50\,\mathrm{g} \nonumber \\ m_\mathrm{Ca} &\ge 1000\,\mathrm{mg} \nonumber \\ m_\mathrm{Fe} &\ge 18\,\mathrm{mg}, \label{eq:manj-omejitev} \end{aligned}\end{equation} dobimo dieto na sliki 1 zgoraj. Takoj zaznamo pomenljivost modela v tem, da ne omejujemo količine zaužitega natrija. Če bi lahko brez težav zaužili večje količine soli, bi to namreč predstavljalo ugoden nizko-kaloričen vir kalcija (slika 1 zgoraj). Zato osnovnim omejitvam (3) dodamo še omejitve \begin{equation}\begin{aligned} m_\text{vitamin C} &\ge 60\,\mathrm{mg} \nonumber \\ m_\text{K} &\ge 3500\,\mathrm{mg} \nonumber \\ m_\text{Na} &\in [500\,\mathrm{mg}, 2400\,\mathrm{mg}] \label{eq:dodatne-omejitve} \end{aligned}\end{equation} tako pa dobimo nekoliko bolj realistično dieto na sliki 2 zgoraj. Vidimo, da je radenska nizko-kaloričen (oz. nič-kaloričen) vir kalcija in natrija, kakav pa v dieti nastopa kot nekakšno super-živilo, saj preko \(500\,\mathrm{g}\) kakava pridobimo večino drugih potrebnih hranil, razen vitamina C (tega pridobimo preko pomaranče).

Omejevanje količine posameznega živila

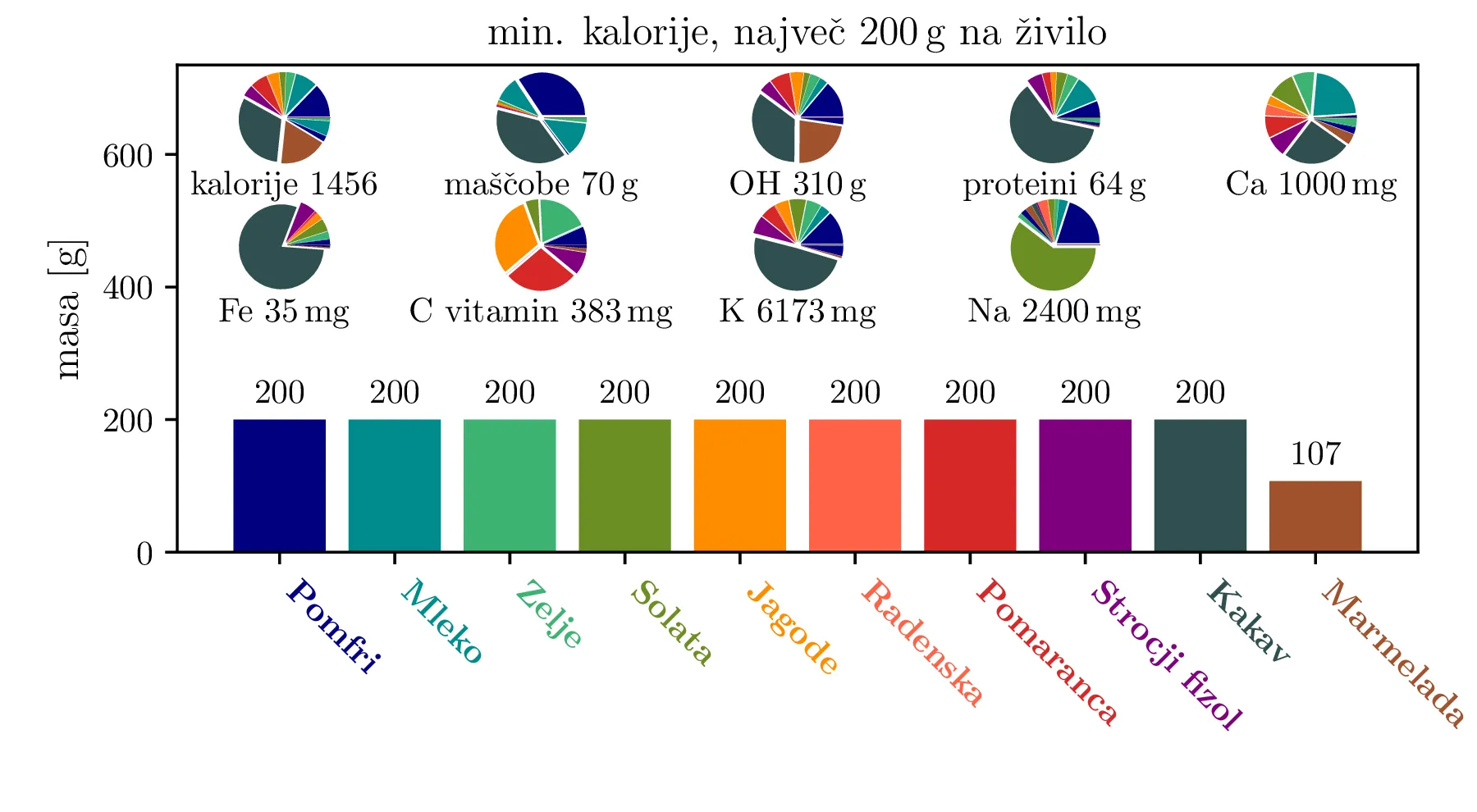
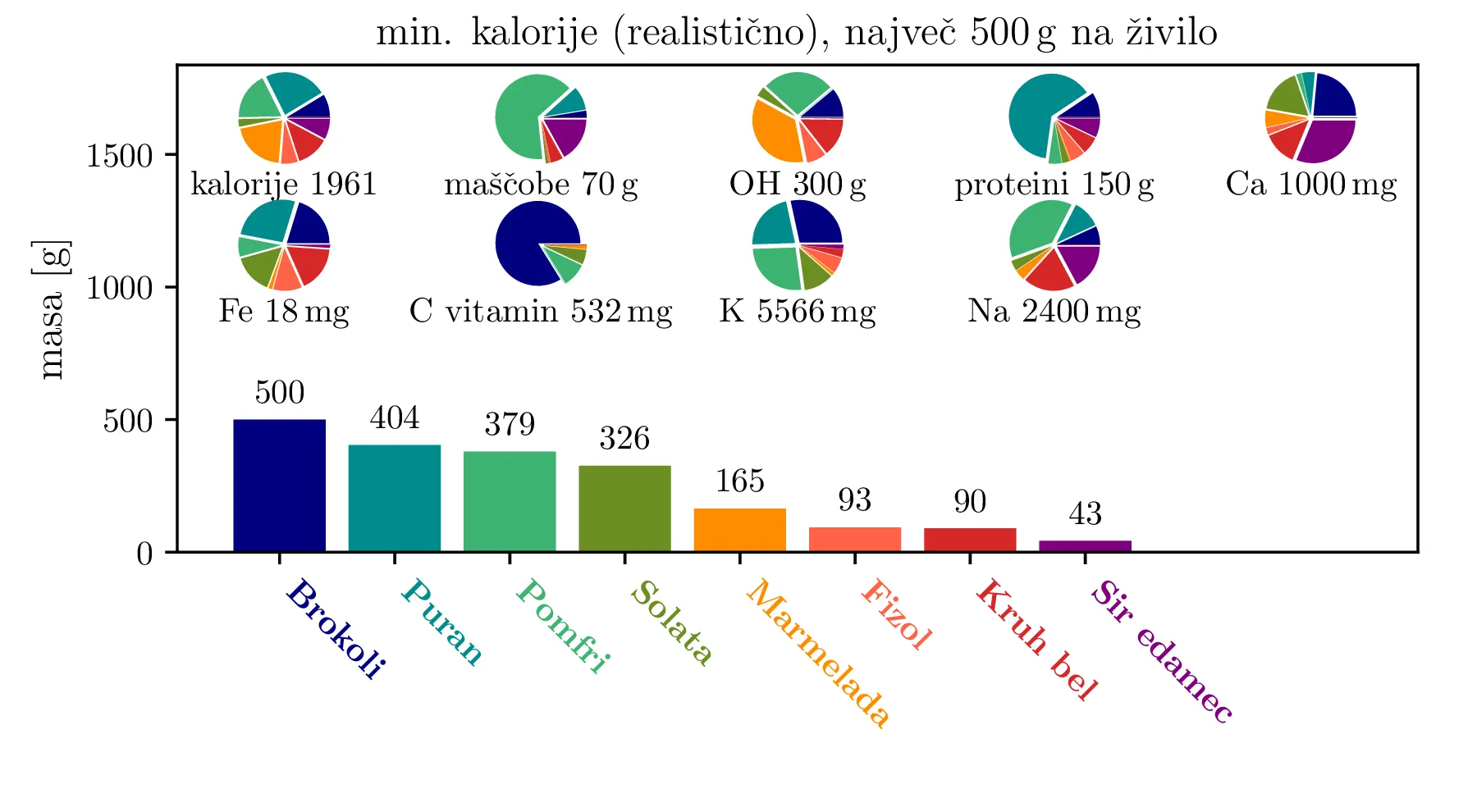
Depresivna je misel na dieto, kjer zaužijemo nesorazmerno veliko količino enega živila. Zato uvedemo maksimalno količino za vsako posamezno živilo. Za živila \(j = 1, 2, 3, \dots\) to izrazimo matrično kot vezi \[\begin{bmatrix} -\mathbf{e}_\mathrm{1}^T \\ -\mathbf{e}_\mathrm{2}^T \\ -\mathbf{e}_\mathrm{3}^T \\ \vdots \end{bmatrix} \le \begin{bmatrix} m_\text{max. na živilo} \\ m_\text{max. na živilo} \\ m_\text{max. na živilo} \\ \vdots \end{bmatrix},\] torej kar z \(I_N\) identitetno matriko za \(N\) različnih živil. Vse diete, ki jih bomo določili, izračunamo še s to dodatno omejitvijo. Tako pridobljene diete za omejitvi \(500\,\mathrm{g}\) in \(200\,\mathrm{g}\) na posamezno živilo vidimo na kot sredinsko in spodnjo figuro na slikah 1, 2, 3, 4 in 4.

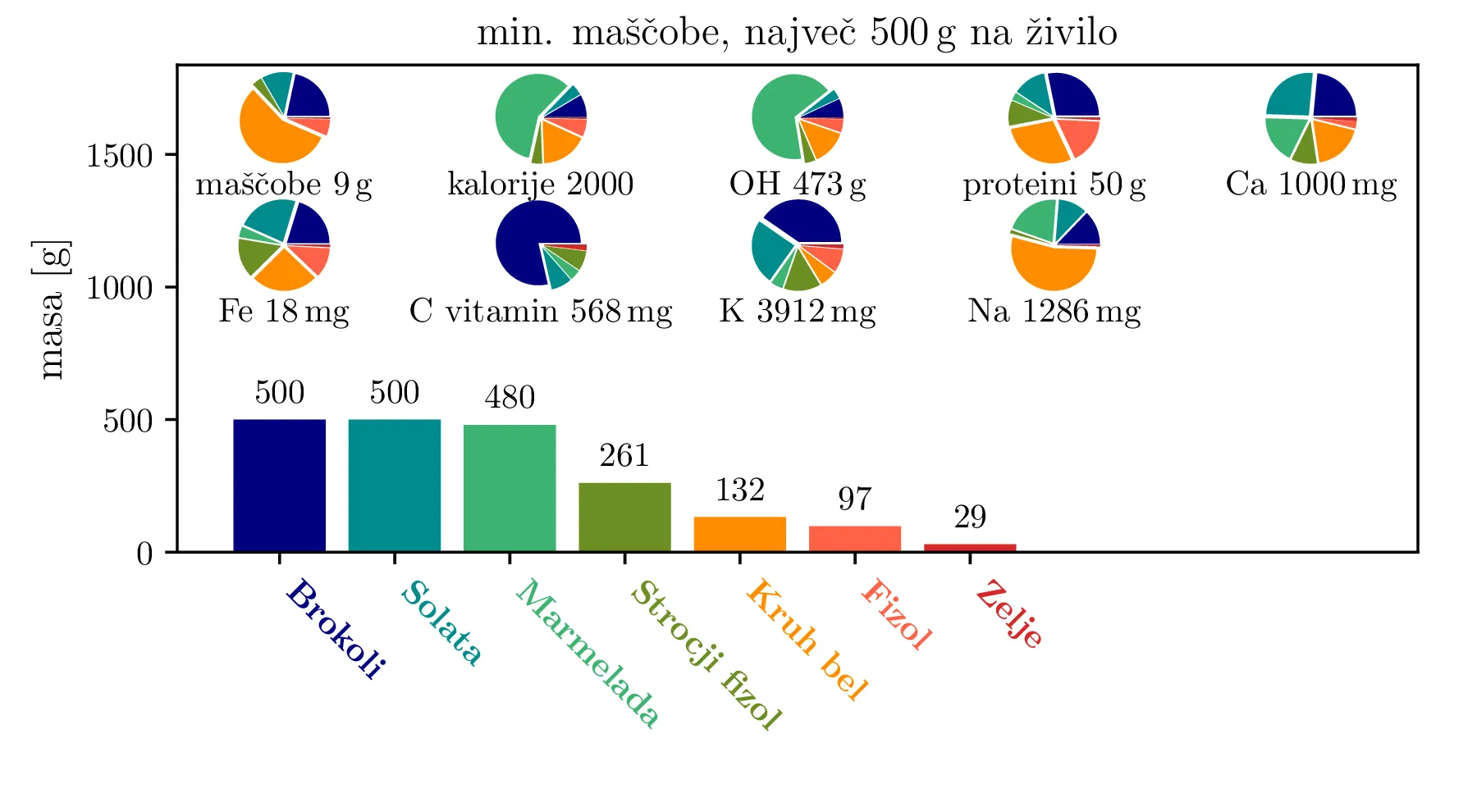
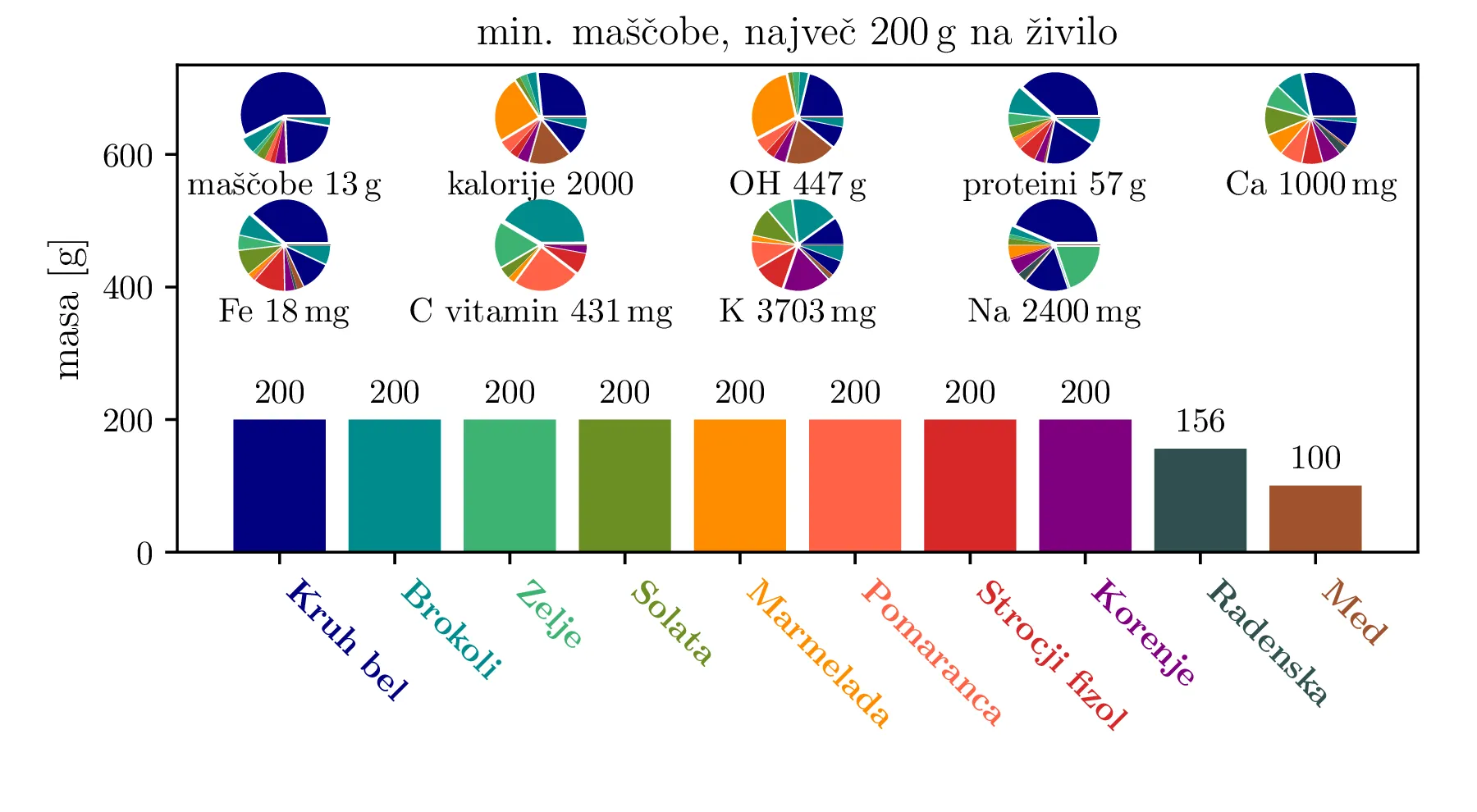
Minimizacija zaužitih maščob

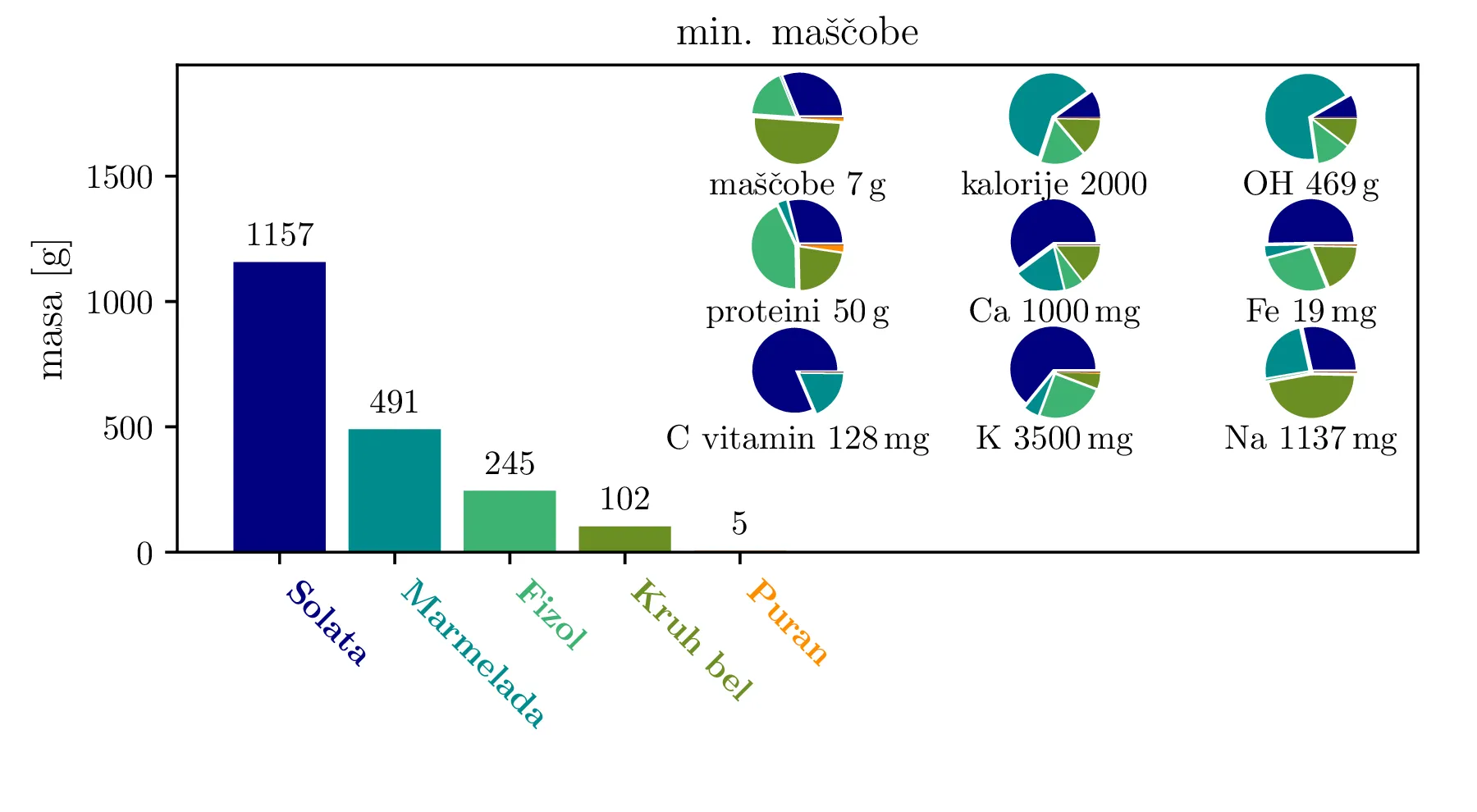
Kot alternativo dieti za hujšanje, kjer zahtevamo čim manjše število zaužitih kalorij, lahko zahtevamo čim manjšo količino zaužitih maščob. Pri tem dodatno omejimo število kalorij, tako da ustreza ravnovesnemu dnevnemu vnosu \[c_\mathrm{cal} \ge 2000.\] Dieta za čim manjšo količino maščob je prikazana na sliki 3.

Minimizacija cene, mornarska dieta

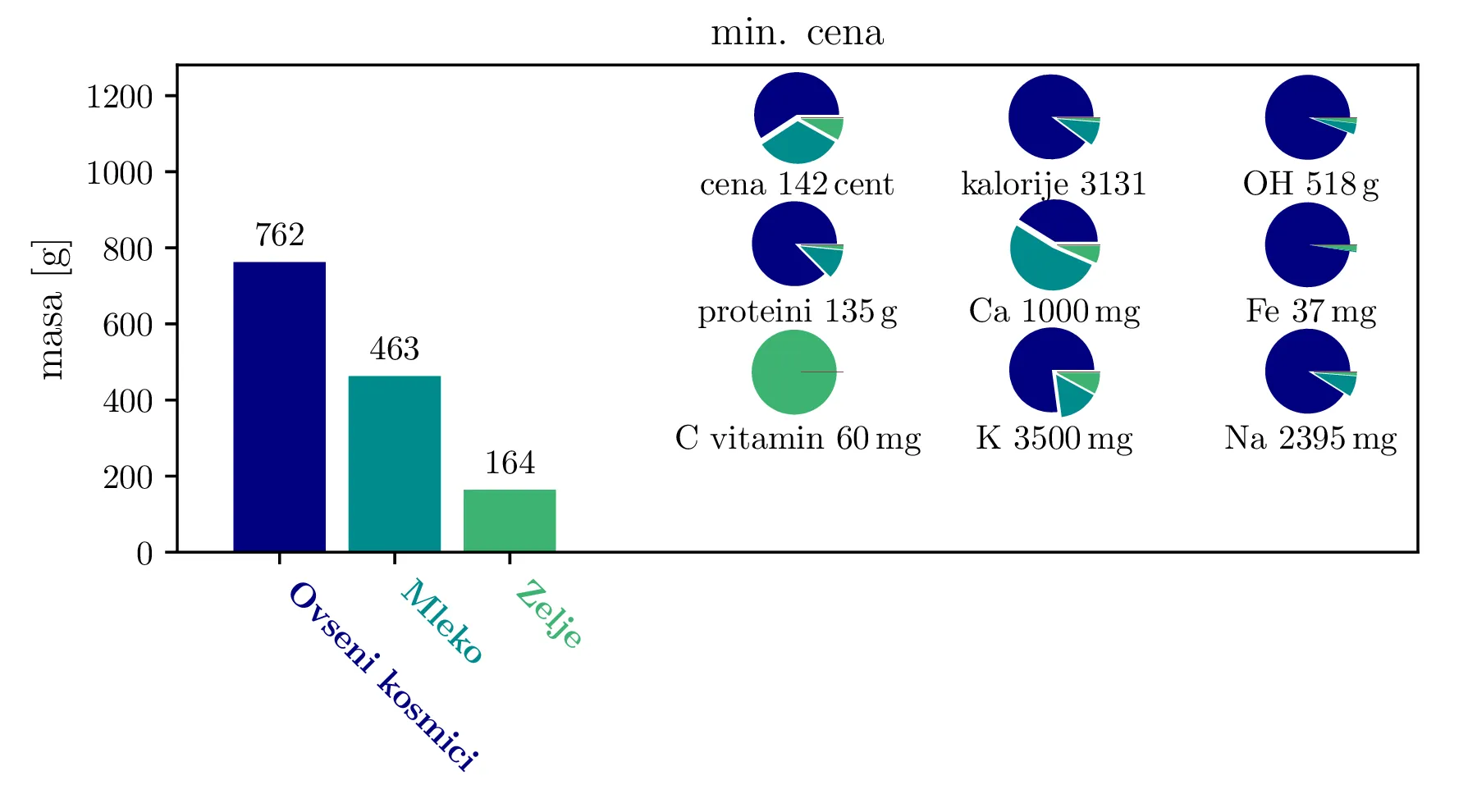
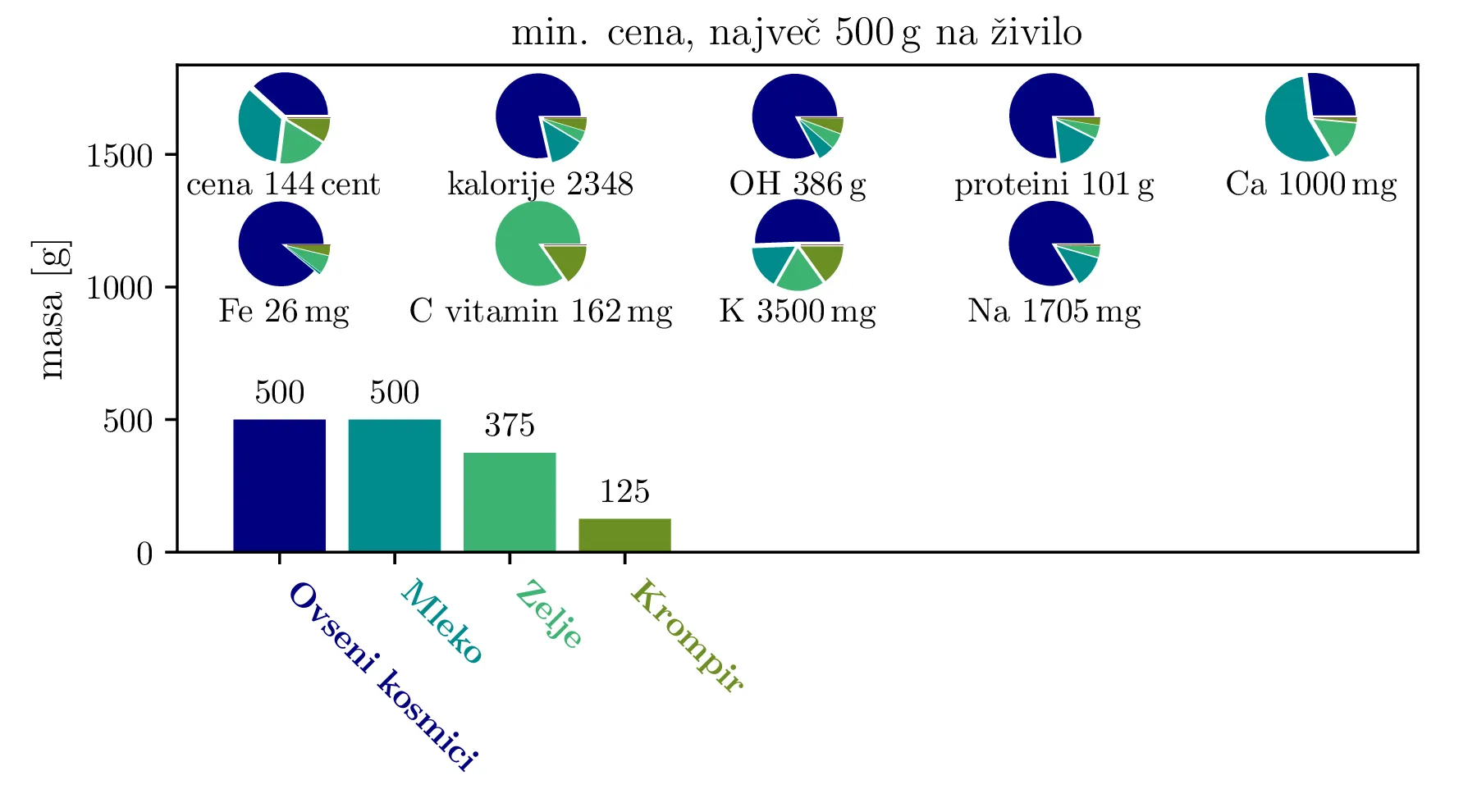
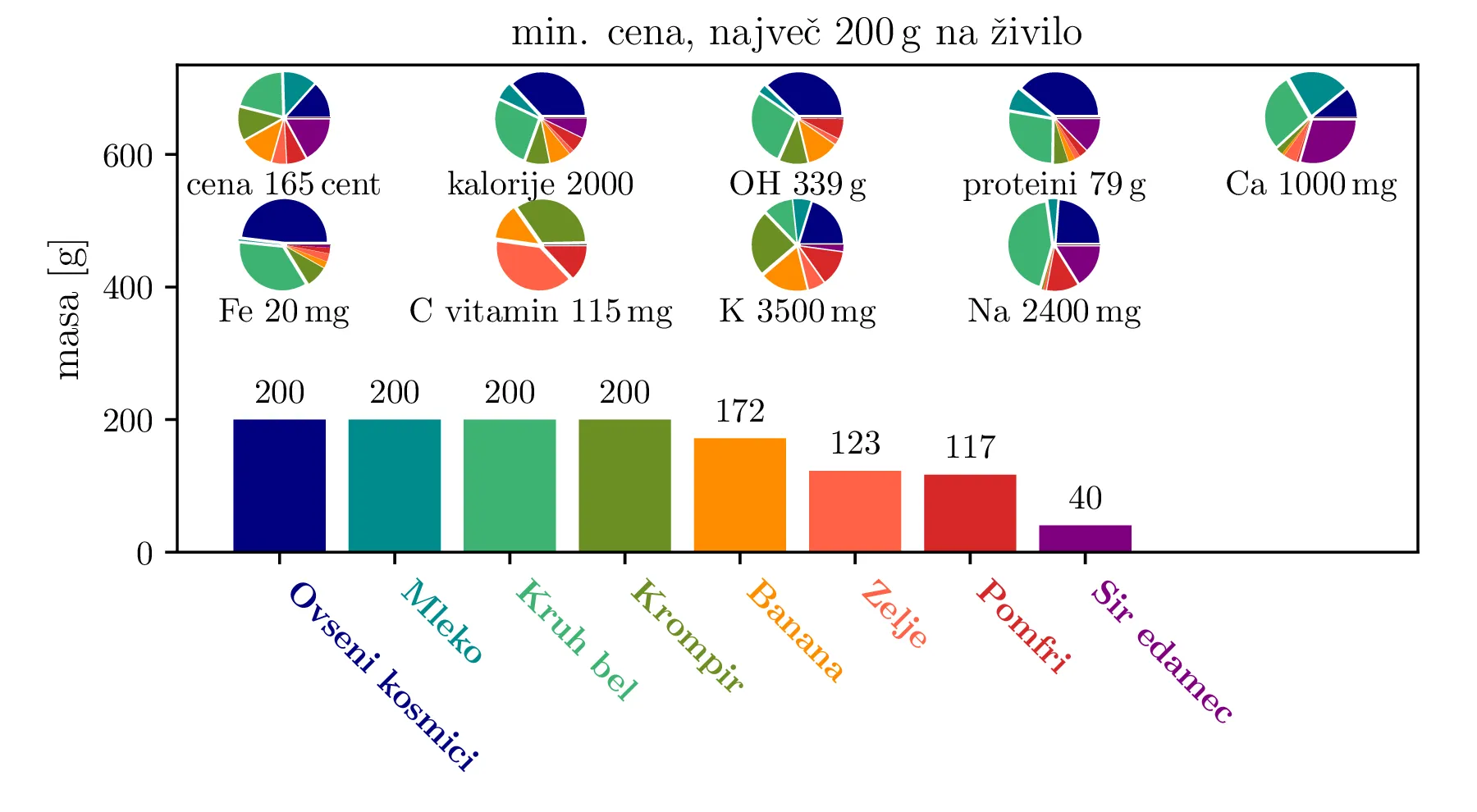
Še en zanimiv kriterij za minimizacijo je cena. Poglejmo si torej, kakšno dieto dobimo, če minimiziramo ceno, hkrati pa še vedno zahtevamo kalorični vnos \(c_\mathrm{cal} \ge 2000\). Dieto, ki jo dobimo (slika 4), bi lahko poimenovali "mornarska dieta". Primarno jo namreč sestavlja poceni vir ogljikovih hidratov in beljakovin (oves), ki je primeren tudi za dolgoročno shrambo. Dopolnimo ga z mlekom, ki bi ga lahko dobili npr. od koze na ladji. Pomemben in zanimiv pa je tudi dodatek zelja, ki je primarni vir vitamina C, kot kislo zelje v sodih zopet primeren za dolgoročno shrambo.

Realistična dieta

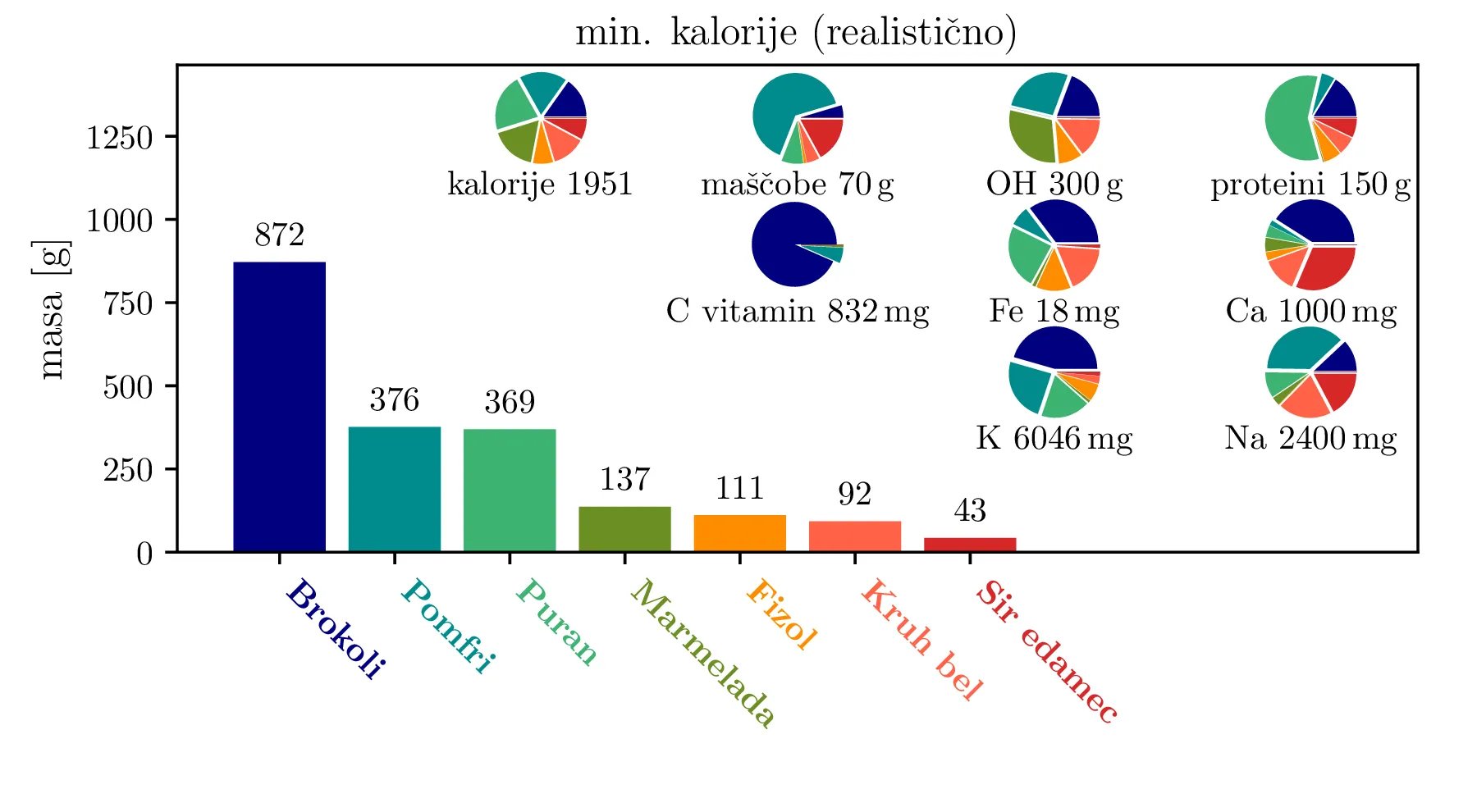
Poskusimo z linearnim modelom predpisati še nekoliko bolj realistično dieto. Naš cilj lahko ostane najmanjše število zaužitih kalorij, torej je cilj hujšanje. Ker je pri hujšanju velik problem neželena izguba mišične mase, bomo nekoliko povečali zahtevano količino beljakovin \begin{equation}\begin{aligned} m_\mathrm{maščobe} &\ge 70\,\mathrm{g} \nonumber \\ m_\mathrm{OH} &\ge 300\,\mathrm{g} \nonumber \\ m_\mathrm{proteini} &\ge 120\,\mathrm{g} \nonumber \\ m_\mathrm{Ca} &\ge 1000\,\mathrm{mg} \nonumber \\ m_\mathrm{Fe} &\ge 18\,\mathrm{mg} \nonumber \\ m_\text{vitamin C} &\ge 60\,\mathrm{mg} \nonumber \\ m_\text{K} &\ge 3500\,\mathrm{mg} \nonumber \\ m_\text{Na} &\in [500\,\mathrm{mg}, 2400\,\mathrm{mg}]. \label{eq:real-omejitve} \end{aligned}\end{equation} Iz prejšnjih poskusov očitno, da kakav dominira kot nizkokalorično živilo z zadostno količino beljakovin in maščob. A tako živilo nastopa kot suh prašek, precej neprimeren za uživanje kar v tej obliki. Zato tudi to izločimo iz našega nabora živil. Tako dobljeno "realistično" dieto vidimo na sliki 5.

Problem vožnje skozi semaforje

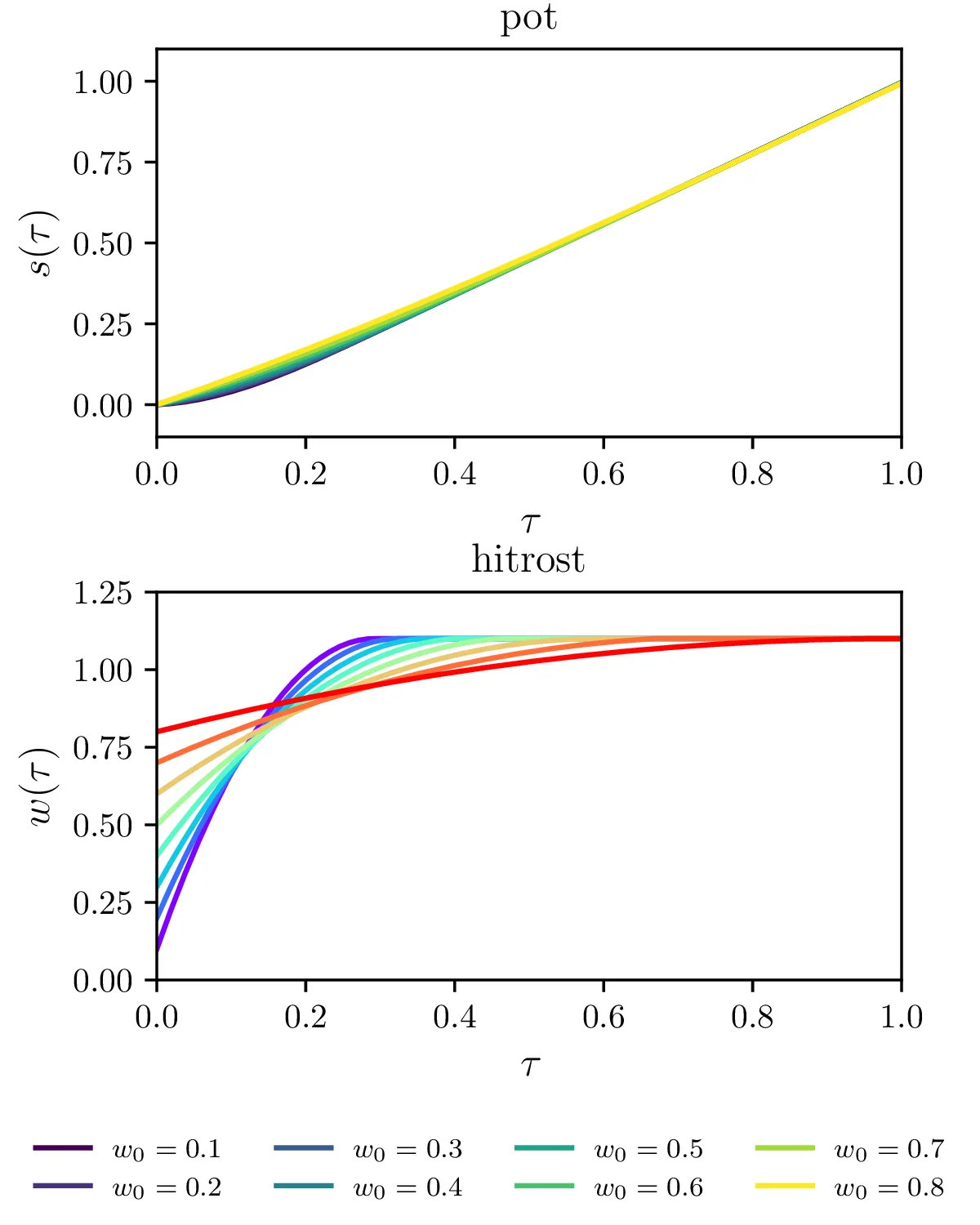
Zdaj bomo s podobno tehniko rešili še problem iz prejšnje naloge². Zelo blizu in podobno linearnemu modelu (2) je njegova preprosta razširitev, kjer je kriterij za minimizacijo oblike \[c = \mathbf{q}^T \mathbf{x} + \mathbf{x}^T H \mathbf{x},\] pri čemer je matrika \(H\) neka pozitivno semi-definitna matrika, t. j. kvadratna forma \(\mathbf{x}^T H \mathbf{x}\) predstavlja nek minimum, ne maksimuma ali sedla. Za optimizacijo kumulativnega kvadrata pospeška prvo določimo pospeške preko končnih diferenc (forward diferenca 1. reda). V matričnem zapisu \begin{equation}\dot{\mathbf{v}} = \begin{bmatrix} \dot{w}_1 \\ \dot{w}_2 \\ \dot{w}_3 \\ \vdots \end{bmatrix} \approx N \begin{bmatrix} w_2 - w_1 \\ w_3 - w_2 \\ w_4 - w_3 \\ \vdots \end{bmatrix} = N \begin{bmatrix} -1 & 1 \\ 0 & -1 & 1 \\ & 0 & \ddots & \ddots \\ & & \ddots & \ddots & 1 \\ & & & 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ \vdots \end{bmatrix} = D_1 \mathbf{w} \label{eq:matrix}\end{equation}

Če želimo čim manjši kumulativni kvadrat pospeška, je optimizacijski kriterij \begin{equation}c = \dot{\mathbf{w}}^T \dot{\mathbf{w}} \approx (D_1 \mathbf{w})^T D_1 \mathbf{w} = \mathbf{v}^T H_1 \mathbf{w}, \label{eq:c-qp}\end{equation} pri čemer je Hessova matrika iz same definicije pozitivno semi-pozitivna \[H_1 = D_1^T D_1 = N^2 \begin{bmatrix} 1 & -1 \\ -1 & 2 & -1 \\ & -1 & 2 & -1 \\ & & -1 & \ddots & \ddots \\ & & & \ddots & \ddots & -1 \\ & & & & -1 & 1 \\ \end{bmatrix},\] in je precej podobna matriki končnih diferenc za \(-\ddot{w}\), razen v zgornjem levem in spodnjem desnem kotu. Pri optimizaciji zahtevamo, da semafor prevozimo ob času \(\tau = 1\), kar ustreza linearni vezi \begin{equation}1 = \int_0^1 w \,\mathrm{d}\tau \approx \frac{1}{N} \left( w_1 + w_2 + \dots + w_N \right). \label{eq:vez-0}\end{equation}

Igranje z modelom

Model oblike (7) optimiziramo z modelom iz Python paketa qpsolvers, sicer z solver="proxqp". Da se z modelom lahko nekoliko igram, sem sestavil preprosto aplikacijo (slika 7), kjer lahko prosto nastavljam parametre in vklapljam in izklapljam vezi.

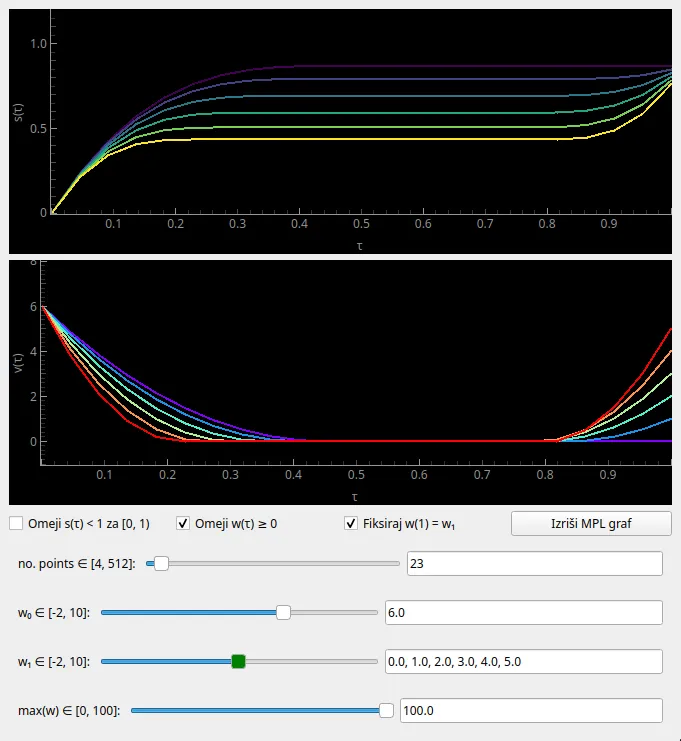
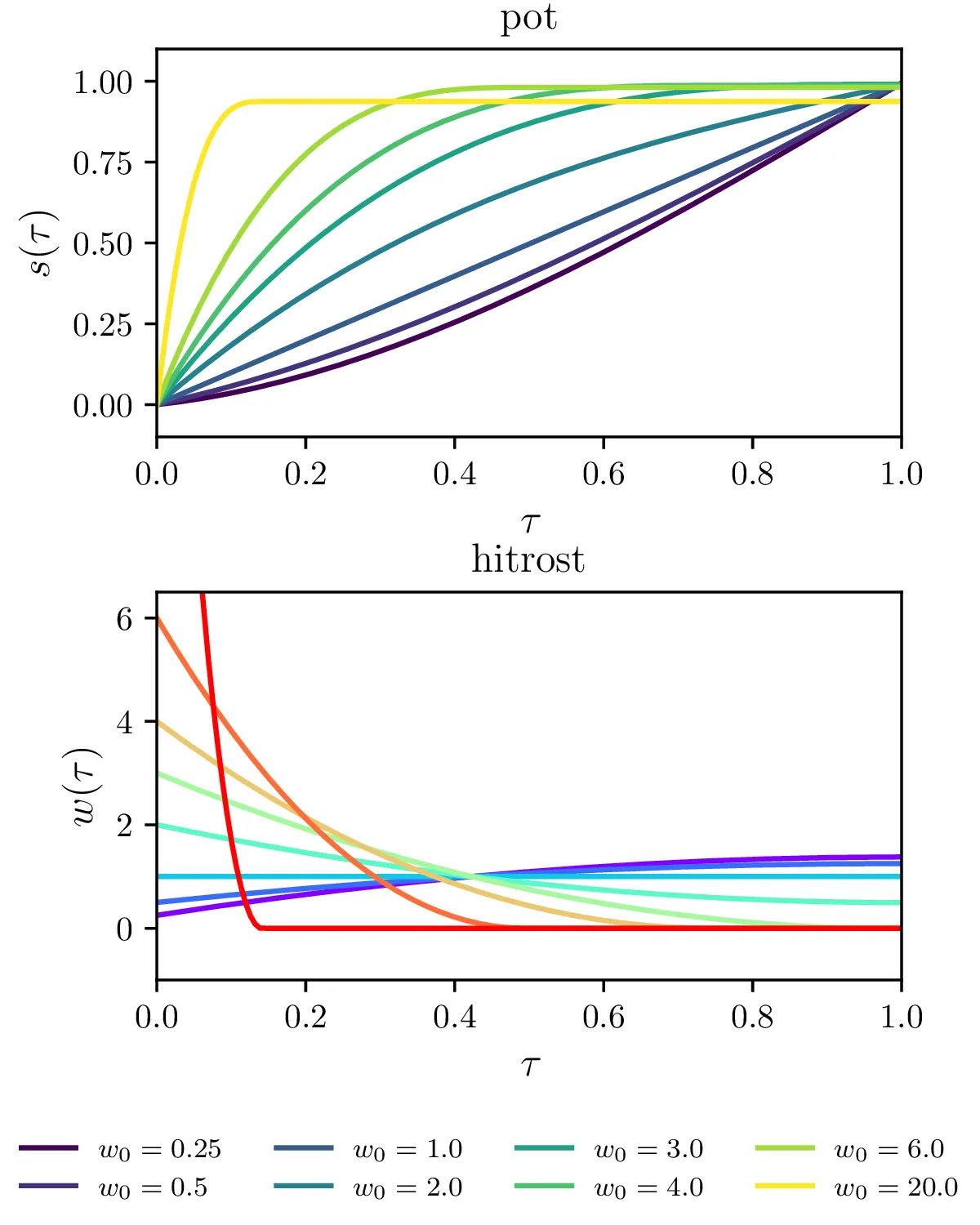
Preprečevanje overshootanje, dva načina

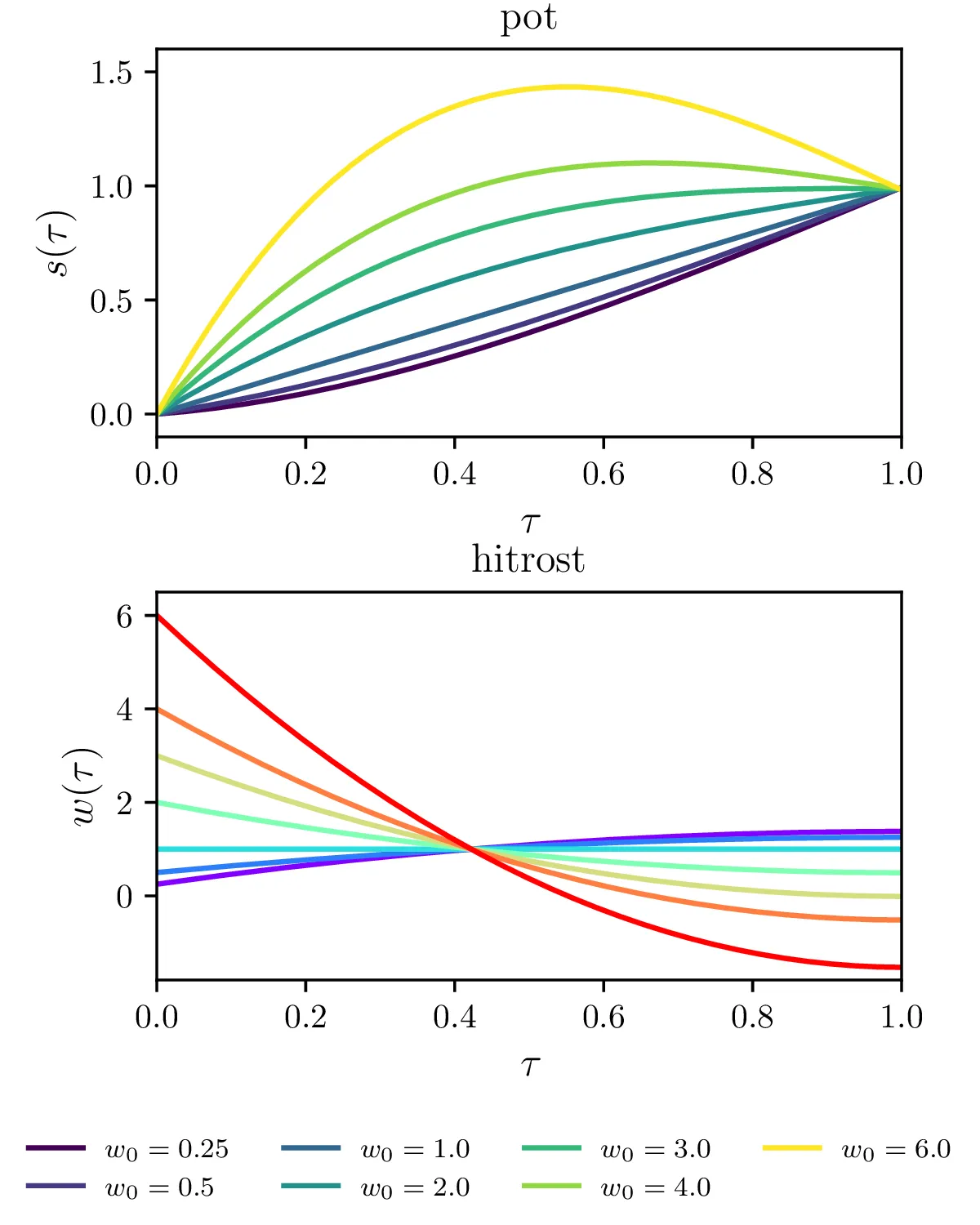
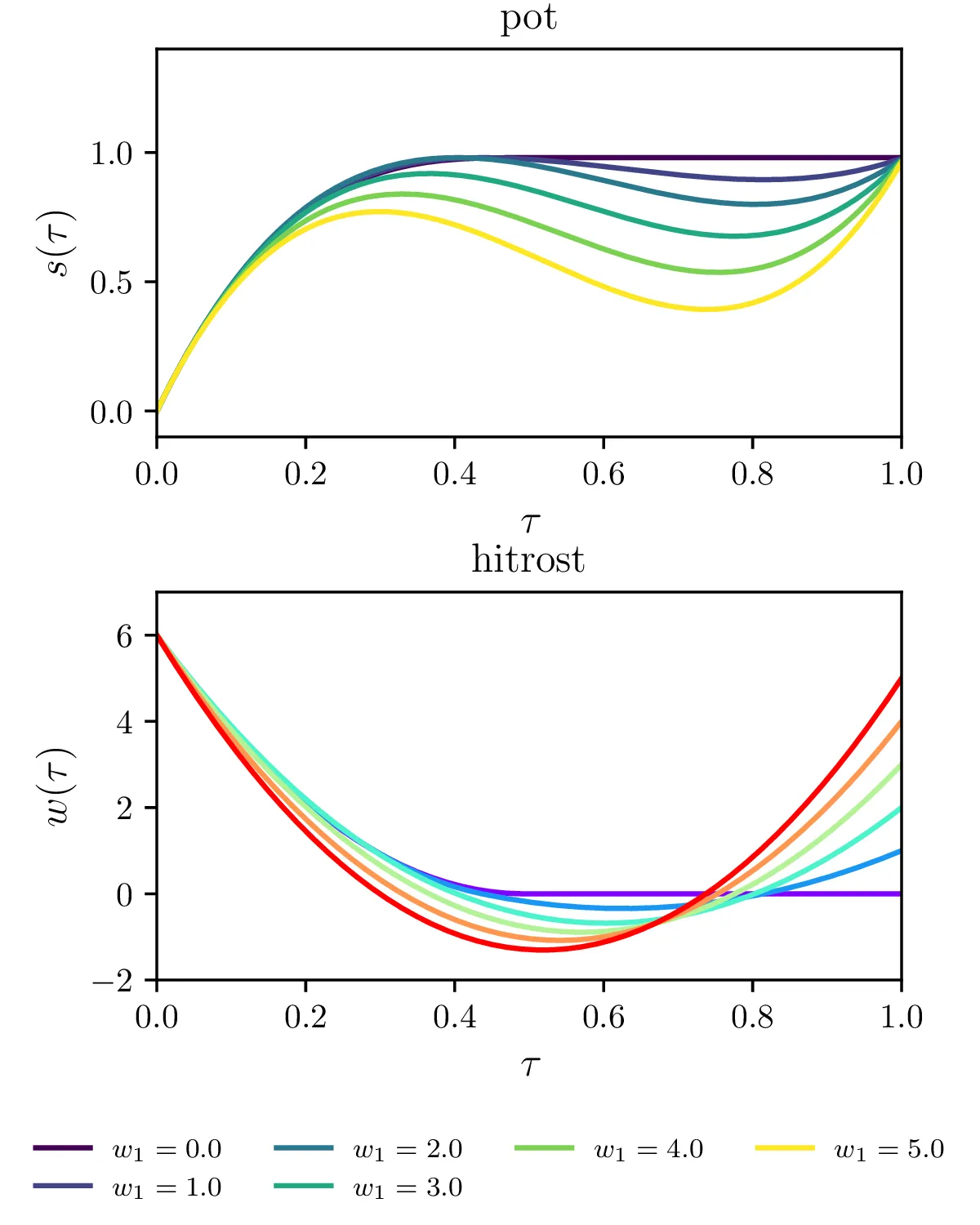
Če želimo zagotoviti tudi, da pred časom \(\tau < 1\) ne prevozimo semaforja, lahko zahtevamo, da je pot manjša od \(1\) tudi za integracijske čase \(\tau_1, \tau_2, \dots, \tau_{N-1}\). V matrični obliki so to (po elementih) vezi oblike \begin{equation}\frac{1}{N} \begin{bmatrix} 1 & \dots & 1 & 1 & 1 & 0 \\ 1 & \dots & 1 & 1 & 0 & 0 \\ 1 & \dots & 1 & 0 & 0 & 0 \\ \vdots \\ 1 & 1 & 0 & \dots & 0 & 0 \\ 1 & 0 & 0 & \dots & 0 & 0 \\ \end{bmatrix} \mathbf{v} \le 1. \label{eq:vez-A}\end{equation} Sicer bolj stroga vez kot to, da ne smemo prevoziti semaforja, je totalna prepoved vzvratne vožnje \begin{equation}\mathbf{w} \ge 0. \label{eq:vez-B}\end{equation} Na prvi pogled se zdi, da je vez (10) strožja kot (9). A igranje z modelom na sliki 8 kaže, da delujeta povsem ekvivalentno. Šele ko dodamo vez za fiksno končno hitrost \[w_N = w_1,\] opazimo (slika 9) razliko med poteki glede na to, ali upoštevamo strožjo vez nenegativnih hitrosti (10) ali manj restriktivno vez (9).

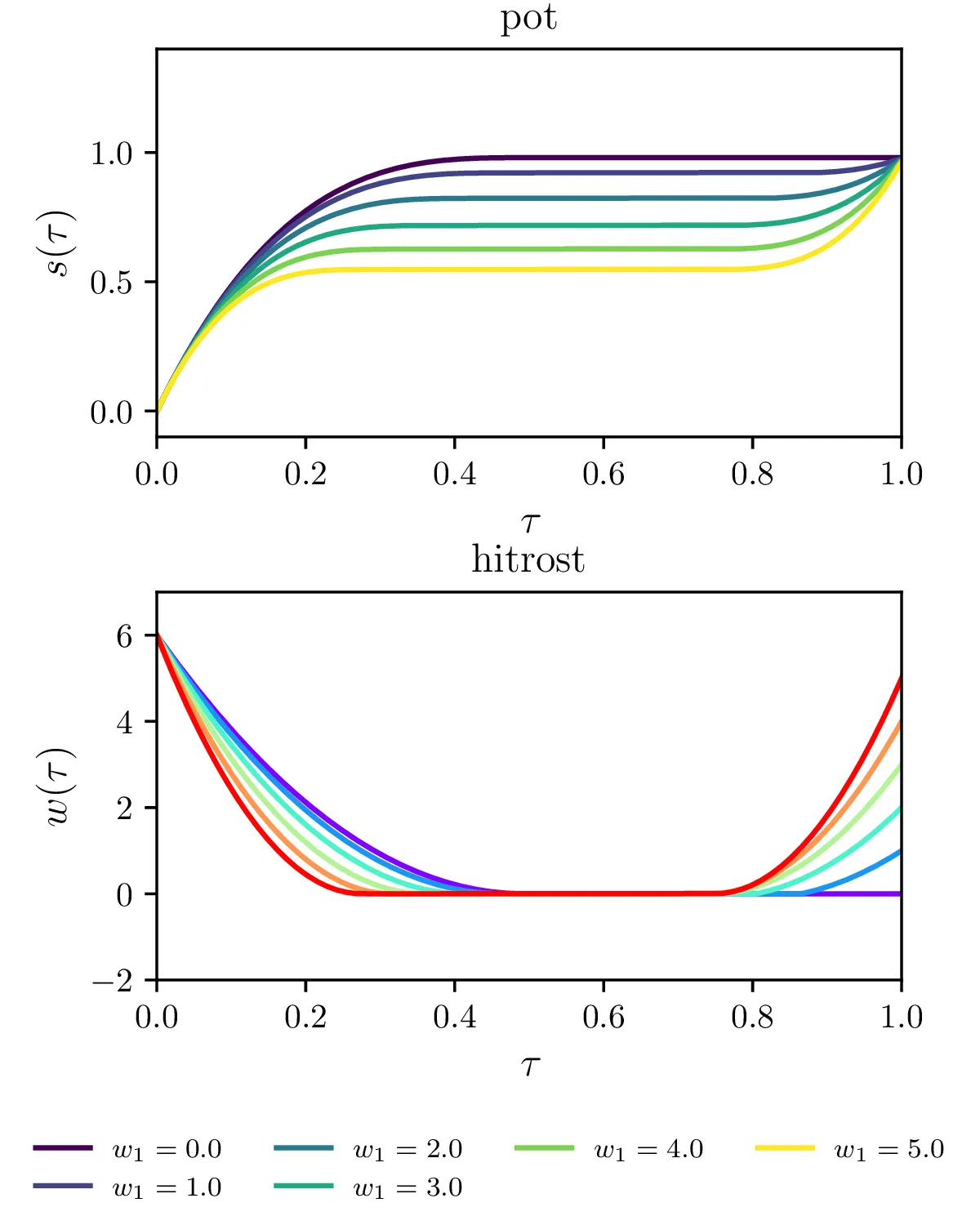
Omejitev hitrosti

V modelu lahko zelo preprosto upoštevamo tudi hitrostne omejitve. Sicer kot \begin{equation}I \mathbf{v} \le v_\text{max}. \label{eq:vez-MAX}\end{equation} Efekt te omejitve vidimo, ko je začetna hitrost nizka (glede na \(1\)), omejitev pa je le nekoliko večja od \(1\), da ravno še omogoča potovanje za pot \(1\) v danem času (slika 10). Tedaj je potovanje relativno neudobno, saj je potreben velik pospešek (na omejitev), da lahko semafor še dosežemo.