Optimalna vožnja

Model vožnje skozi semafor, pristop z variacijsko metodo

Navodila

Varčno vožnjo lahko definiramo s pogojem, da je pospeševanja in zaviranja čim manj. To lahko dosežemo z minimizacijo kurulativnega kvadrata pospeška. Isčemo optimalni režim vožnje v situaciji, ko poskušamo razdaljo do semaforja prevoziti ravno v trenutku, ko se prižge zelena luč.

Rešitev

Vožnjo začnemo s hitrostjo \(v_0\), na razdalji \(L\) od semaforja. Iz izkušenj vemo, da se bo semafor prižgal v času \(T\). Ker želimo semafor prevoziti točno ob času \(T\), velja vez \begin{equation}L = \int_0^T v(t) \,\mathrm{d}t. \label{eq:vez}\end{equation} V namen udobne vožnje bomo minimizirali komulativni kvadrat pospeška \(\int \dot{v}^2 \,\mathrm{d}t\). Z upoštevanjem vezi to pomeni minimizacijo z Lagrangianom \begin{equation}\mathcal{L}(v(t), \dot{v}(t)) :=\dot{v}^2 - \lambda v, \label{eq:orig-L}\end{equation} tako da minimiziramo akcijo \[S_\lambda = \int_0^T \dot{v}^2 \,\mathrm{d}t + \int_0^T v \,\mathrm{d}t.\] Nalogo sem reševal s pomočjo Mathematica programskega okolja, to vljučuje reševanje enačb in risanje grafov.

Brezdimenzijska oblika

Za lažje reševanje problema vpeljemo brezdimenzijske količine \begin{equation}\tau :=\frac{t}{T}, \quad u :=\frac{v}{v_0}, \quad \eta :=\frac{L}{v_0 T}, \label{eq:nondim}\end{equation} pri čemer ke \(v_0 T\) nekakšna naravna hitrost, saj pri \(L = v_0 T\) uvidimo trivialno optimalno rešitev v nepospešeni vožnji s konstantno hitrostjo (tako da je akcija kar \(S = 0\)). V takih brezdimenzijskih koordinatah se Lagrangian glasi \[\mathcal{L}'(u(\tau), \dot{u}(\tau)) :=\frac{v_0^2}{T^2} \left[ \dot{u}^2 - \left( \frac{T^2}{v_0} \lambda \right) u \right],\] pri čemer so pike nad črko zdaj odvodi \(\frac{\mathrm{d}}{\mathrm{d}\tau}\) namesto \(\frac{\mathrm{d}}{\mathrm{d}t}\). Lagrangian lahko še nekoliko reskalirano \begin{equation}\mathcal{L}(u(\tau), \dot{u}(\tau)) :=\dot{u}^2 - \left( \frac{T}{v_0^2} \lambda \right) u = \dot{u}^2 - \widetilde{\lambda} u, \label{eq:L}\end{equation} pri čemer je naš novi multiplikator \(\widetilde{\lambda} :=\frac{T^2}{v_0} \lambda\). Če za Lagrangian (4) zapišemo Euler-Lagrange enačbe, dobimo s kratkim računom navadno diferencialno enačbo \begin{equation}\ddot{u} = -\frac{\widetilde{\lambda}}{2}, \quad \tau \in [0, 1], \label{eq:ODE1}\end{equation} z začetnim pogojem \(u(0) = 1\).

Extremalna hitrost pri semaforju

Semafor želimo prevoziti z ekstremalno hitrostjo, tako da velja \(\dot{u}(T) = 0\). Če rešimo navadno diferencialno enačbo 5 in apliciramo pogoja \[\text{odprta robna pogoja: } u(0) = 1, \quad \dot{u}(1) = 0,\] dobimo za rešitev družino krivulj \[u(\tau) = \frac{1}{4} \left( 4 + 2\widetilde{\lambda} t - \widetilde{\lambda} t^2 \right),\] izmed katerih pa je ustrezna samo tista, ki ustreza vezi (1). S preprosto integracijo in obratom dobimo izraz za multiplikator \(\widetilde{\lambda} = 6(\eta - 1)\), s čimer zapišemo rešitev kar po parametru \(\eta\) kot \begin{equation}u(\tau) = 1 + (\eta - 1) \left( 3\tau - \frac{3\tau^2}{2} \right). \label{eq:open-u}\end{equation}

Ničelna začetna hitrost, degeneracija

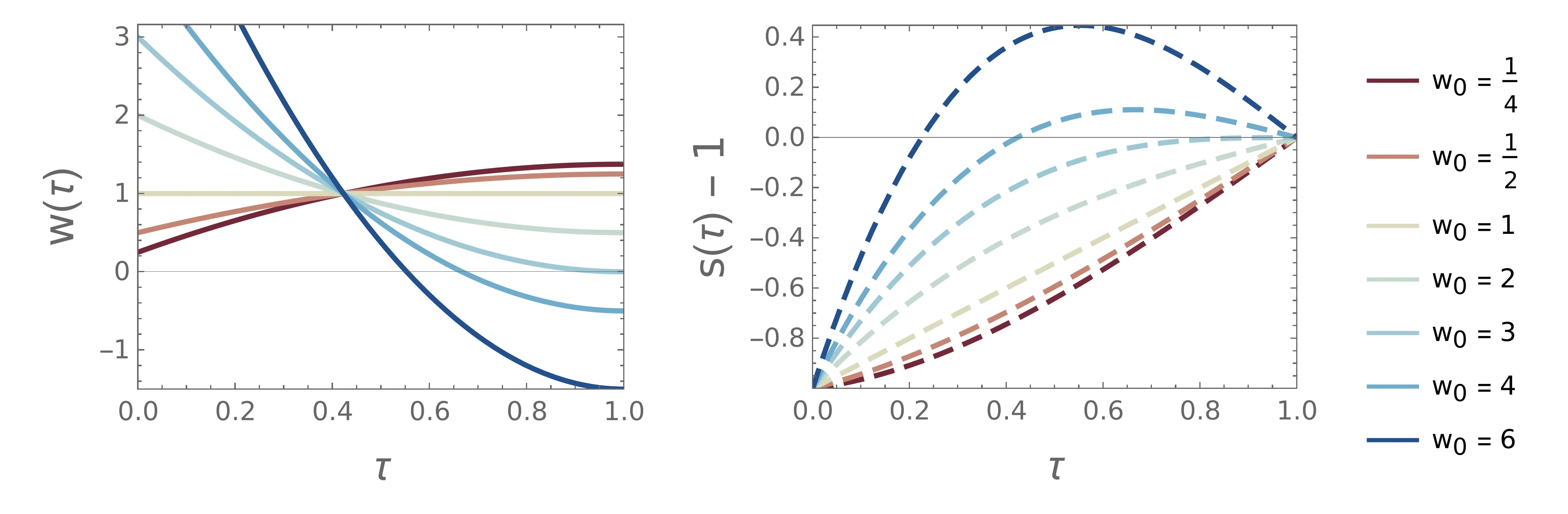
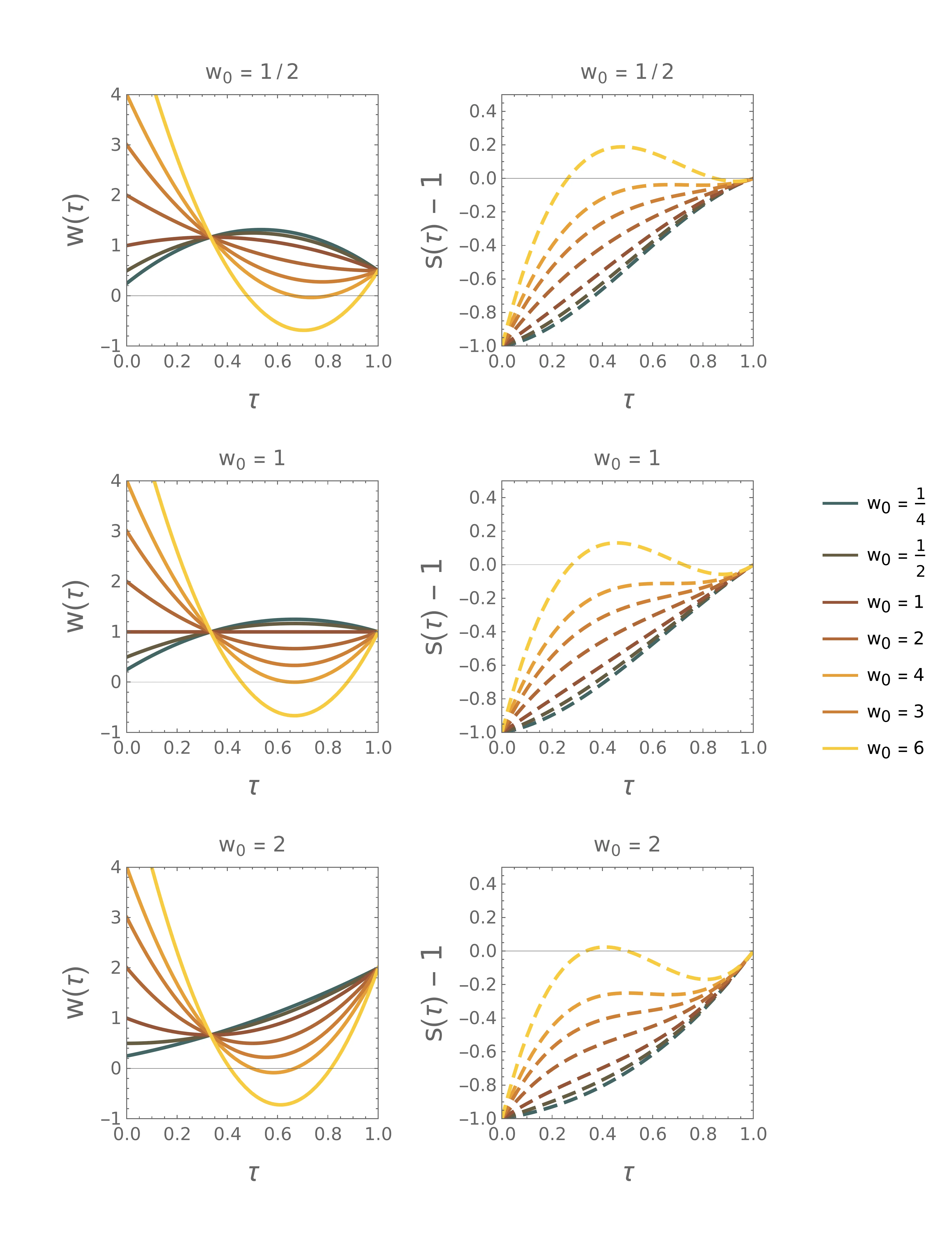
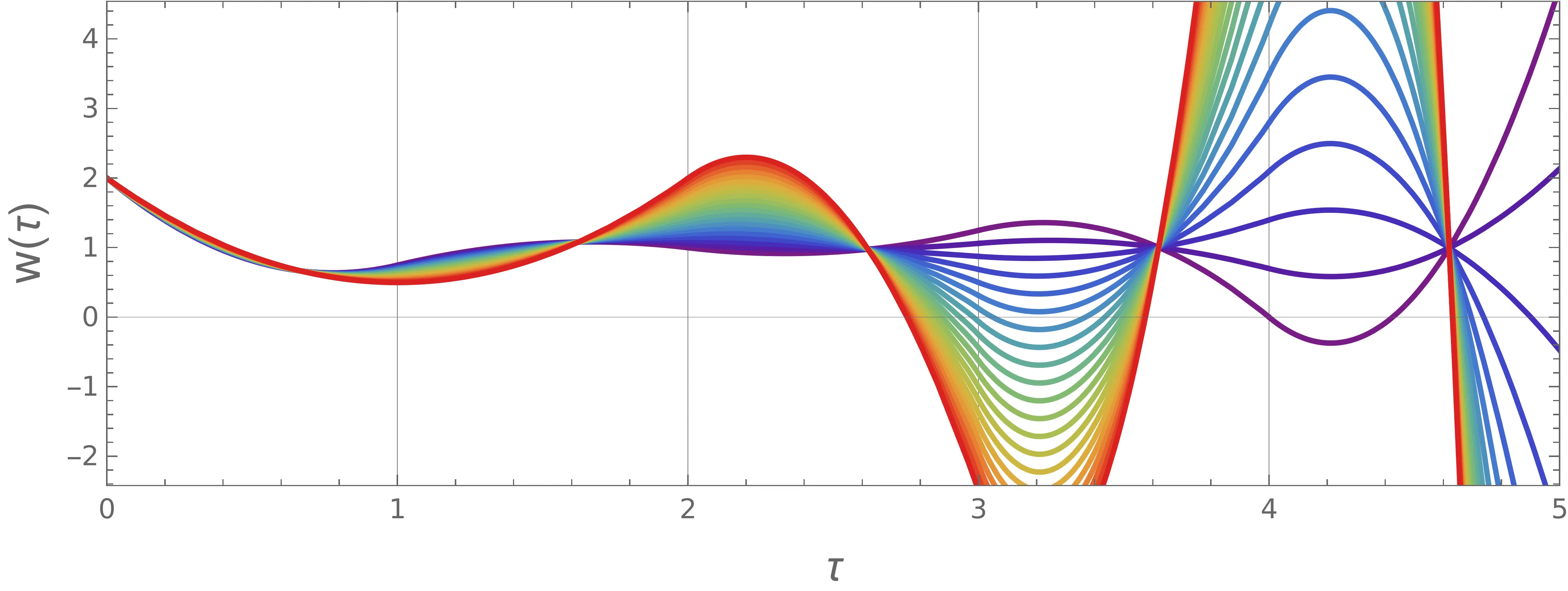
Pri uvedbi brezdimenzijskih količin v 3 smo implicitno predpostavili, da sta \(T, v_0\) neničelna. Za \(T\) je to smiselna predpostavka (in bila bi tudi za \(L\)), a povsem naraven je primer, ko je \(v_0 = 0\). Pri uporabi brezdimenzijskih količin \((\tau, u, \eta)\) bi morali primer \(v_0 = 0\) razrešiti posebej – a bolj elegantno lahko vpeljemo bolj robustne brezdimenzijske količine, ki se tej degeneraciji izognejo \begin{equation}\tau :=\frac{t}{T}, \quad w :=\frac{v}{L/T}, \quad w_0 :=\frac{v_0}{L/T}. \label{eq:nondim2}\end{equation} V novih količninah \((\tau, w, w_0)\) lahko Lagrangian zapišemo kot \begin{equation}\mathcal{L}(w(\tau), \dot{w}(\tau)) :=\dot{w}^2 - \Lambda w, \label{eq:L-new}\end{equation} pri čemer smo podobno kot pri starih količinah vpeljali nov multiplikator \(\Lambda :=\frac{T^3}{L}\lambda\). Sama diferencialna enačba za rešitve ostaja enaka kot (5), le z \(\Lambda\) namesto \(\widetilde{\lambda}\) in z robnimi pogoji \begin{equation}\text{odprta robna pogoja: } w(0) = w_0, \quad \dot{w}(1) = 0, \label{eq:open-boundary}\end{equation} s čimer je rešitev oblike \begin{equation}w(\tau) = w_0 + \frac{\Lambda}{4} \left(2\tau - \tau^2 \right), \label{eq:open-lambda-ODE}\end{equation} izmed njih pa izberemo tisto, ki ustreza vezi \(\int_0^1 w \,\mathrm{d}\tau = 1\). Z vstavljanjem dobljenega \(\Lambda\) nazaj v izraz za \(w(\tau)\), dobimo odvisnost hitrosti \begin{equation}w(\tau) = w_0 + (1-w_0) \left( 3\tau - \frac{3\tau^2}{2} \right). \label{eq:open-w}\end{equation} da smo z uvedbo drugih brezdimenzijskih enot, kjer je namesto brezdimenzijske poti \(\eta\) ključni parameter brezdimenzijska začetna hitrost \(w_0\), pridobili lepše obnašanje v degeneriranem primeru \(v_0 = 0\). Na sliki 2 lahko vidimo obliko rešitve (11), ko spreminjamo začetno hitrost \(w_0\).

Fiksna hitrost pri semaforju

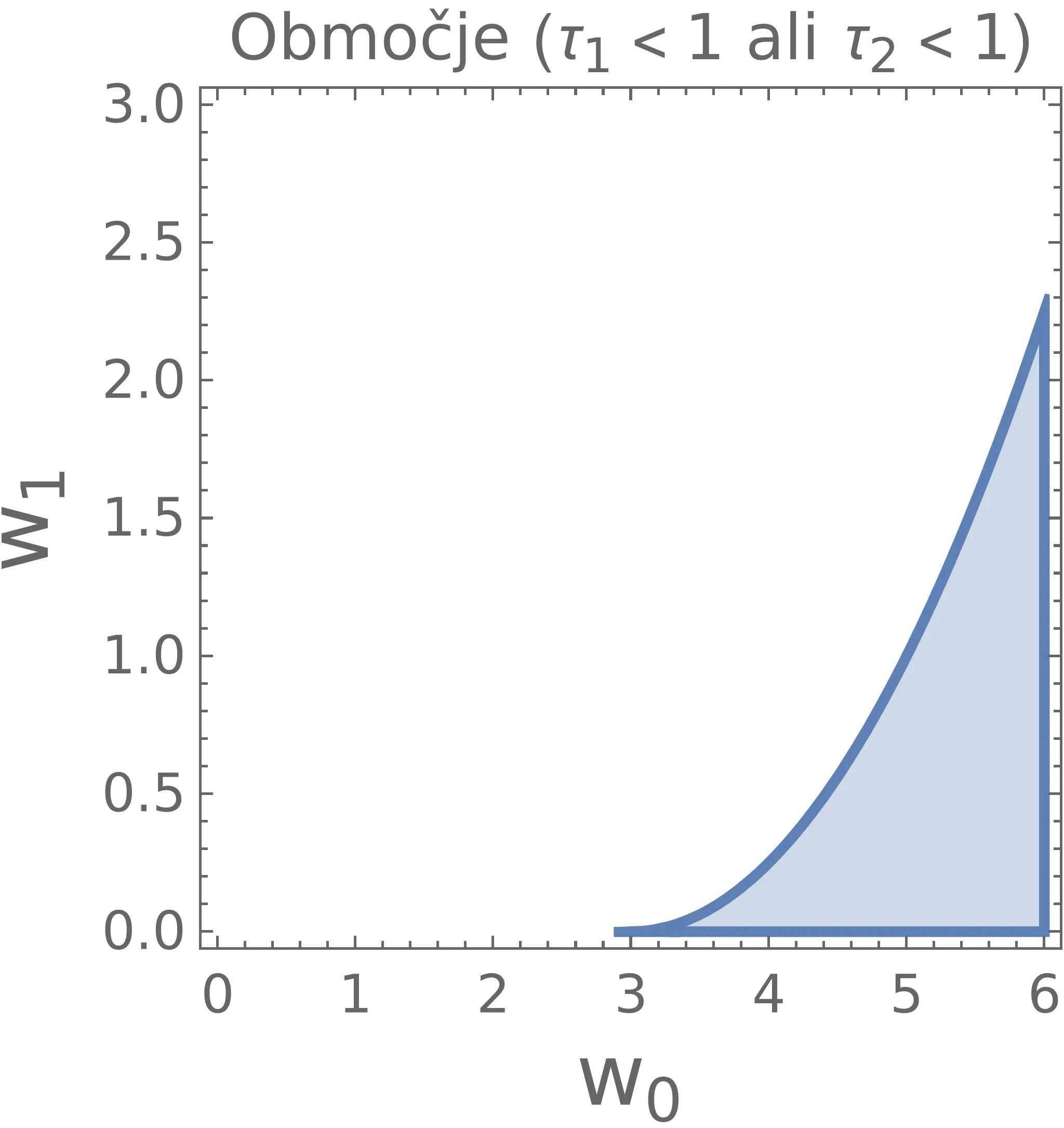
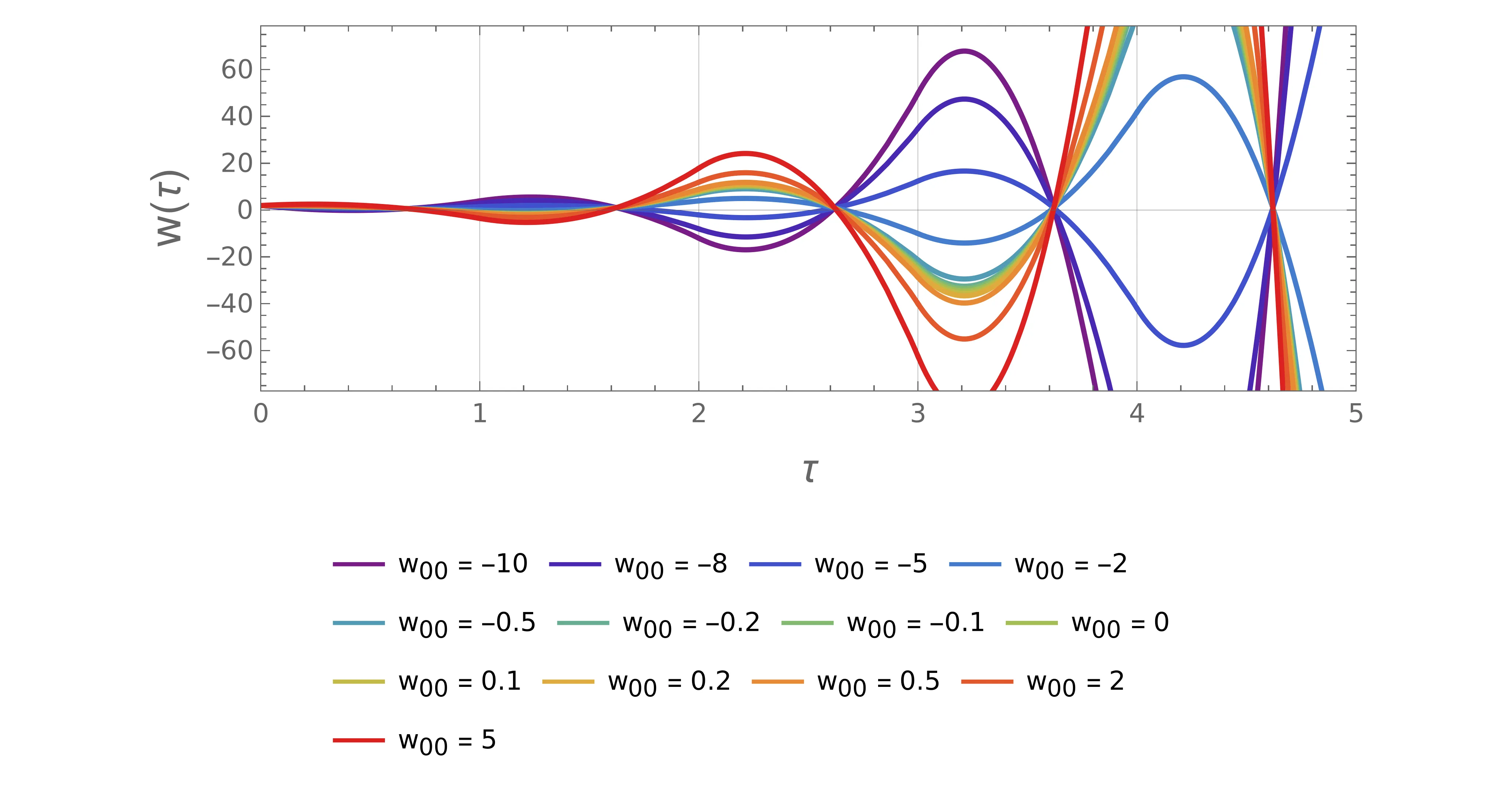
Alternativa odprtemu robnemu pogoju \(\dot{w}(1)=0\) je t. i. zaprto robni pogoj, kjer je končna hitrost pri semaforju točno določena. Spet rešujemo navadno diferencialno enačbo (5), le z robnimi pogoji \begin{equation}\text{zaprta robna pogoja: }\quad w(0) = w_0, \quad \dot{w}(1) = w_1. \label{eq:closed-boundary}\end{equation} Rešitev enačbe \begin{equation}w(\tau) = w_0 + 2\tau (3-2w_0-w_1) - 3\tau^{2} (2-w_0-w_1). \label{eq:closed-w}\end{equation} Rešitev (13) je parametrizirana z dvema prostima parametroma \(w_0, w_1\), poteke za nabor teh dveh parametrov narišemo na sliki 1.

Višje potence pospeška

Raziskati bi želeli še rešitve z Lagrangianom, ki kaznuje člen \({\dot{w}}^p\) za splošno potenco \(p\), ne le za \(p=2\). Zapišemo \begin{equation}\mathcal{L}_p(w(\tau), \dot{w}(\tau)) :=\dot{w}^{p} - \Lambda w, \quad p \in \mathbb{N}. \label{eq:L-2p}\end{equation} Lagrangian oblike 14 nam preko Euler-Lagrange enačbe porodi diferencialno enačbo \[p(p-1) \dot{w}^{(p-2)} \ddot{w} = -\Lambda.\] Če enačbo rešujemo kar v tej obliki z DSolve in odprtim robnim pogojem (9), nam Mathematica izpljune zelo grdo rešitev. Pomagamo ji tako, da enačbo razdelimo na dve enačbi \[\begin{aligned} \dot{Z}(\tau) &= -\Lambda, \quad\quad Z(1) = 0,\\ Z(\tau) &= p \dot{w}^{(p-1)}, \quad w(0) = w_0, \end{aligned}\] tako dobimo pomožno rešitev \(Z(t) = \Lambda (1-\tau)\), na podlagi tega pa Mathematica lepo reši drugo enačbo \[\Lambda (1-\tau) = p \dot{w}^{(p-1)}, \quad w(0) = w_0.\] Glede te enačbe lahko omenimo še en detajl. Ker je čas \(\tau \in [0, 1]\), mora biti za \(p > 2\) naš \(\Lambda > 0\), drugače enačba ni rešljiva v \(\mathbb{R}\). Ta pomislek tudi upraviči, da ignoriramo opozorilo, ki nam ga vrne DSolve, sicer:

Solve: Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information.

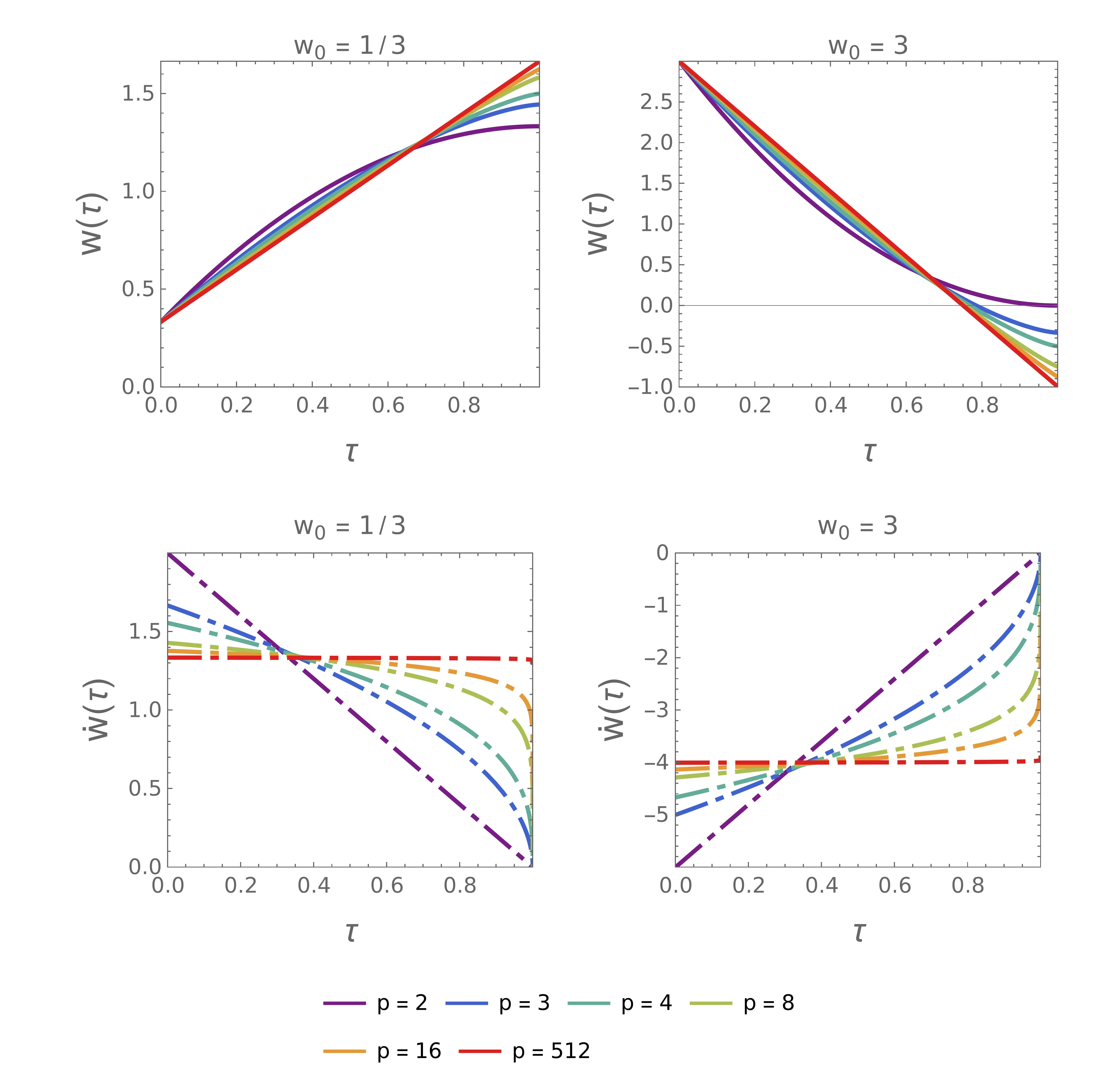
Dobljeno rešitev malce poenostavimo na roke in zapišemo \begin{equation}w(\tau) = w_0 + \frac{p-1}{p} \left( \frac{\Lambda}{p} \right)^{\frac{1}{p-1}} \left( 1 - \left[ 1-\tau \right]^{\frac{p}{p-1}} \right). \label{eq:2p-lambda-ODE}\end{equation} Takoj lahko preverimo, da je za \(p=2\) enačba (15) kar enake oblike kot (10). Preostane nam le še vez \(\int_0^1 w\,\mathrm{d}\tau = 1\). Ko integiramo (15), upoštevamo že prej upravičeno predpostavko \(\Lambda > 0\). Ko dobljeno enačbo rešimo za \(\Lambda\) in vsavimo nazaj v (15), dobimo končno obliko rešitve \begin{equation}w(\tau) = w_0 + \frac{(2p-1)(1-w_0)}{p} \left( 1 - \left[ 1-\tau \right]^{\frac{p}{p-1}} \right). \label{eq:2p-w}\end{equation} Na sliki 3 vidimo, kako povečevanje eksponenta \(p\) vpliva na optimalne rešitve. Ko se \(p\) veča, postajajo rešitve vedno bolj podobne limitni premici \[w(\tau) = w_0 + 2t(1-w_0).\] Še vedno pa (vsaj v limitnem smislu) velja, da je \(\dot{w}(1) = 0\), čeprav je padec na \(\dot{w} = 0\) vedno bolj oster za višje \(p\) (slika 3 spodaj).

Kvadratni člen v hitrosti

Če poleg velikosti pospeška smatramo kot neuodobno tudi višjo absolutno hitrost, lahko zapišemo Lagrangian z dodatnim \(w^2\) členom \begin{equation}\mathcal{L}_\chi(w(\tau), \dot{w}(\tau)) :=\dot{w}^2 + \chi^2 w^2 - \Lambda w. \label{eq:L-chi}\end{equation} Euler-Lagrange enačbe za tak Lagrangian nam dajo \begin{equation}\ddot{w} - \chi^2 w = -\frac{\Lambda}{2}. \label{eq:ODE2}\end{equation} Če diferencialno enačbo (18) rešujemo z odprtim robnim pogojem, dobimo rešitev oblike \[w(\tau) = e^{-\Lambda\chi\tau} \frac{\Lambda e^{\chi\tau} + \Lambda e^{\chi(2+t)} - [\Lambda - 2\chi^2 w_0](1 + e^{\chi t})e^{\chi t} }{2\chi^2 (1+e^{2\chi})}.\] Ko upoštevamo vez za razdaljo, dobimo za multiplikator vrednost \[\Lambda = \frac{2\chi^2 (\chi - w_0 \tanh\chi)}{\chi - \tanh\chi}.\] Tako 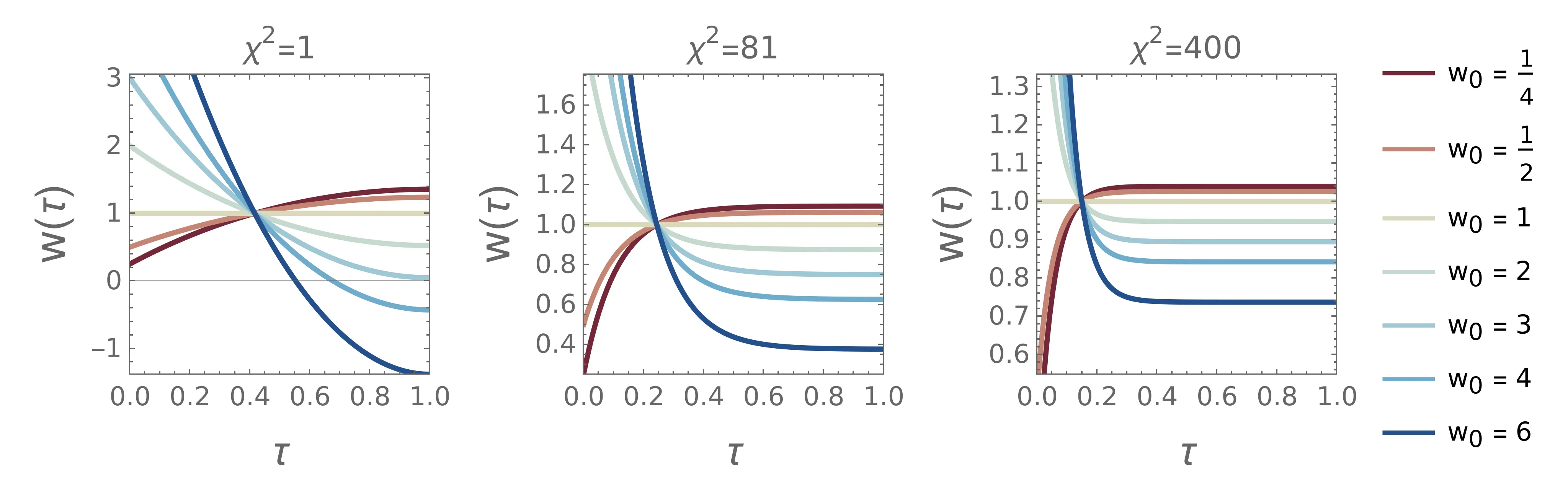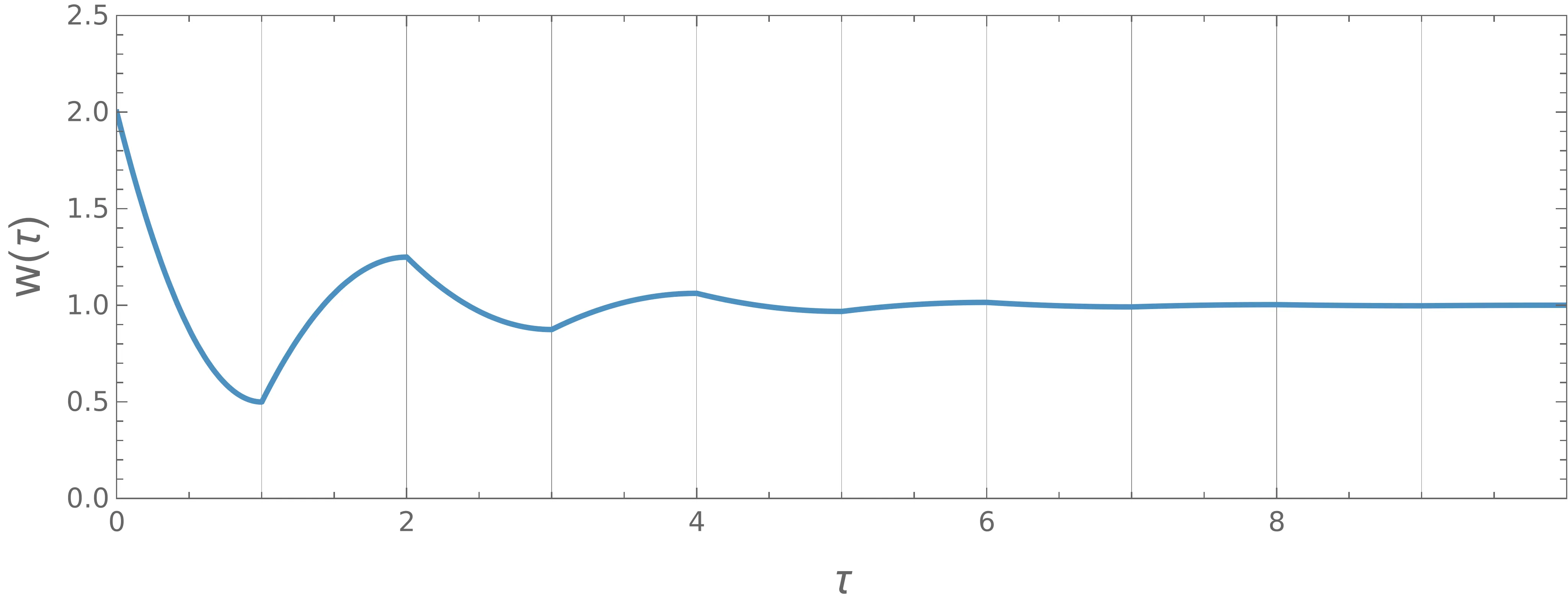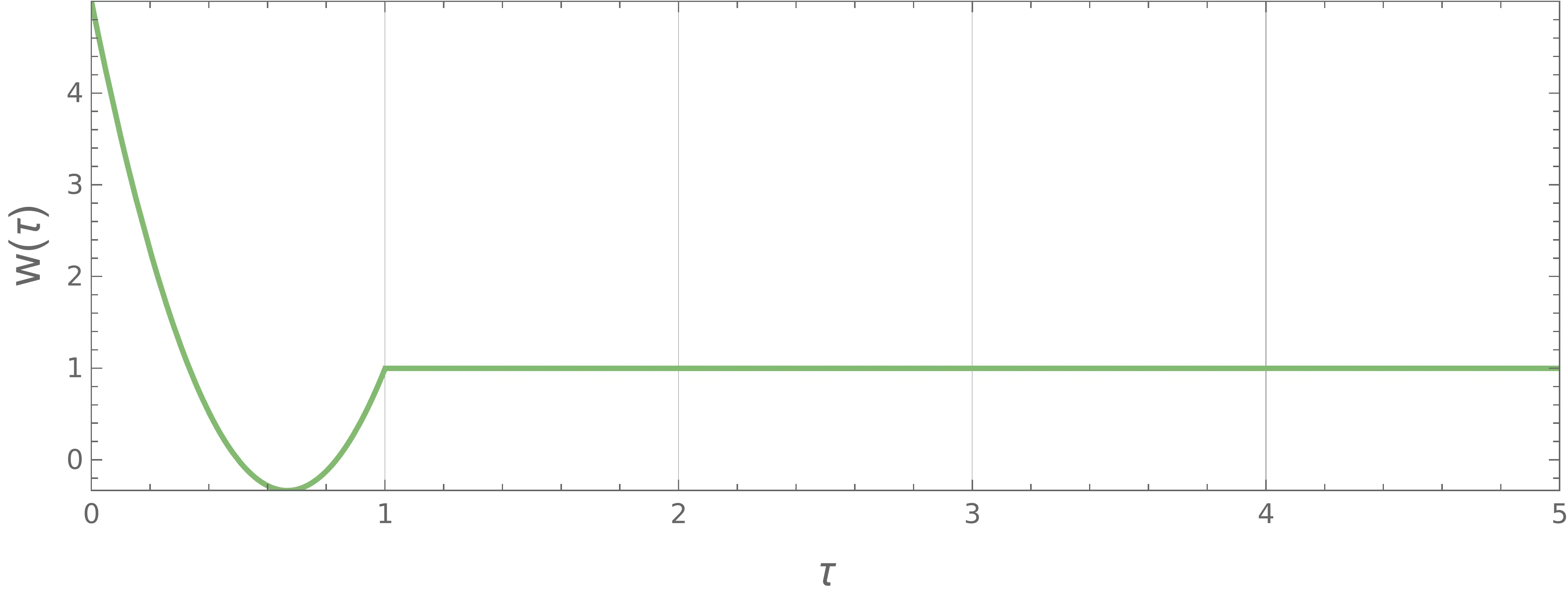dobljen \(w(\tau)\) narišemo na sliki 4. Na sliki 5 še bolj eksplicitno pokažemo vpliv večjega \(\chi^2\)¹ faktorja na potek \(w(\tau)\). Vidimo, da se ob večjem \(\chi\) (bolj močno kaznovana hitrost) začne pojavljati v osrednjem delu \(\tau \in (0, 1)\) vedno bolj izrazit plato (ang. plateau), kjer je \(w\) konstantna. Ker zahtevamo neko določeno površino pod krivuljo \(w(\tau)\), hitrost \(w\) kaznujemo s kvadratnim pribitkom \(w^2\), je optimalna oblika kar konstanta. Vse druge oblike so manj optimalne, saj je pribitek na posamezne dele, ki štrlijo ven iz platoja, kvadraten.

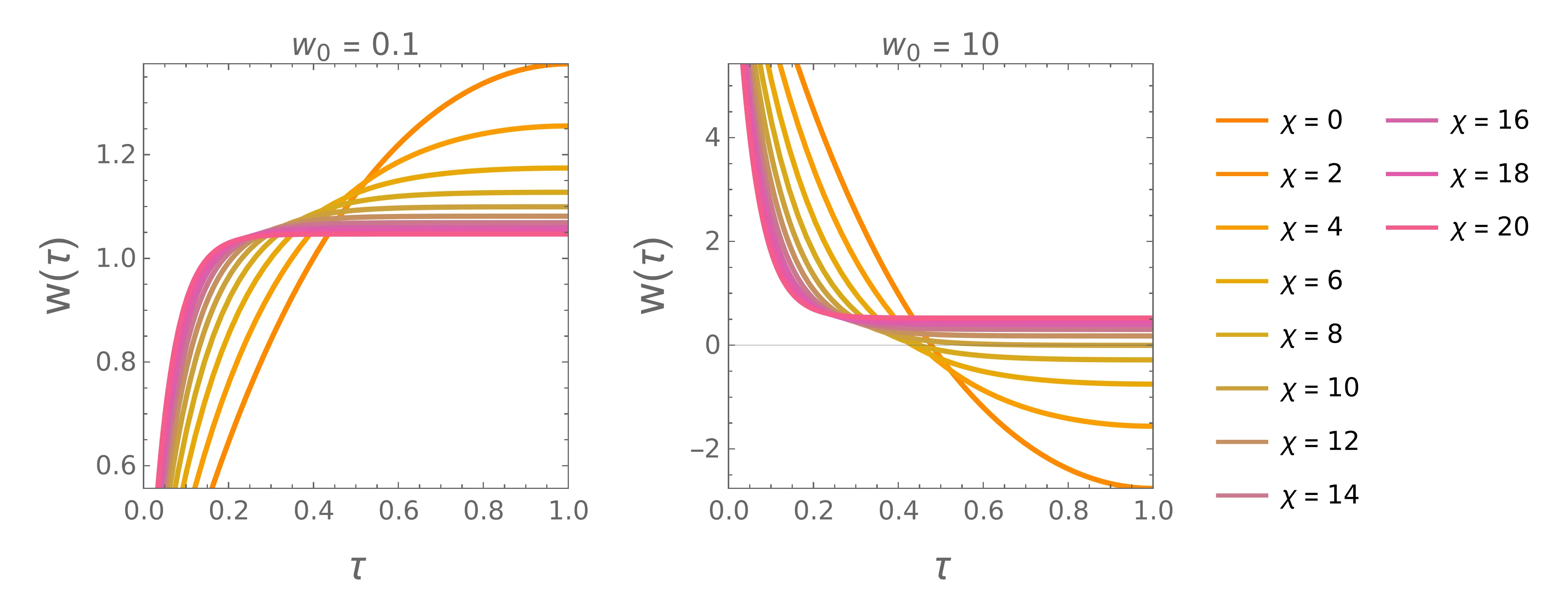
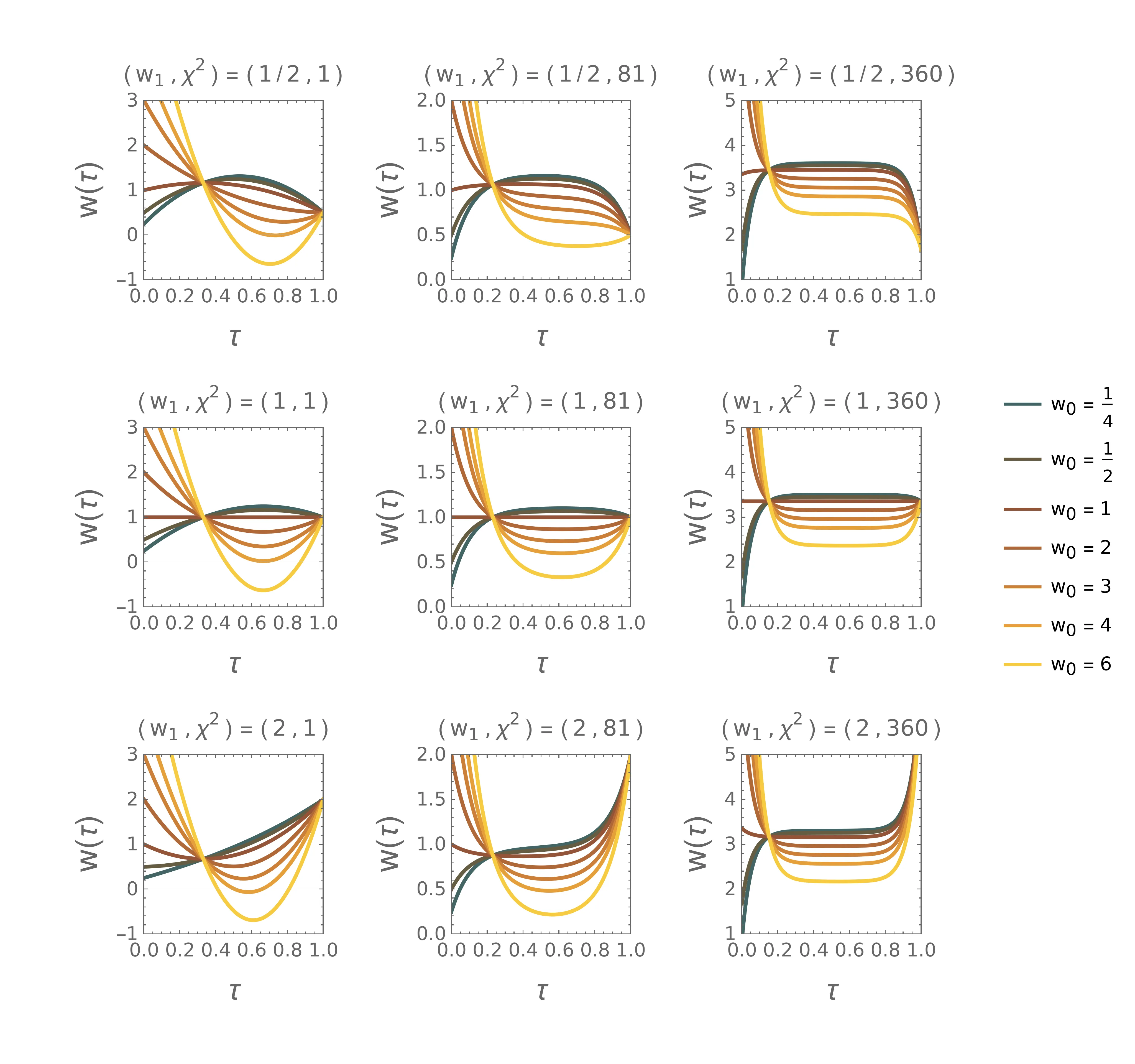
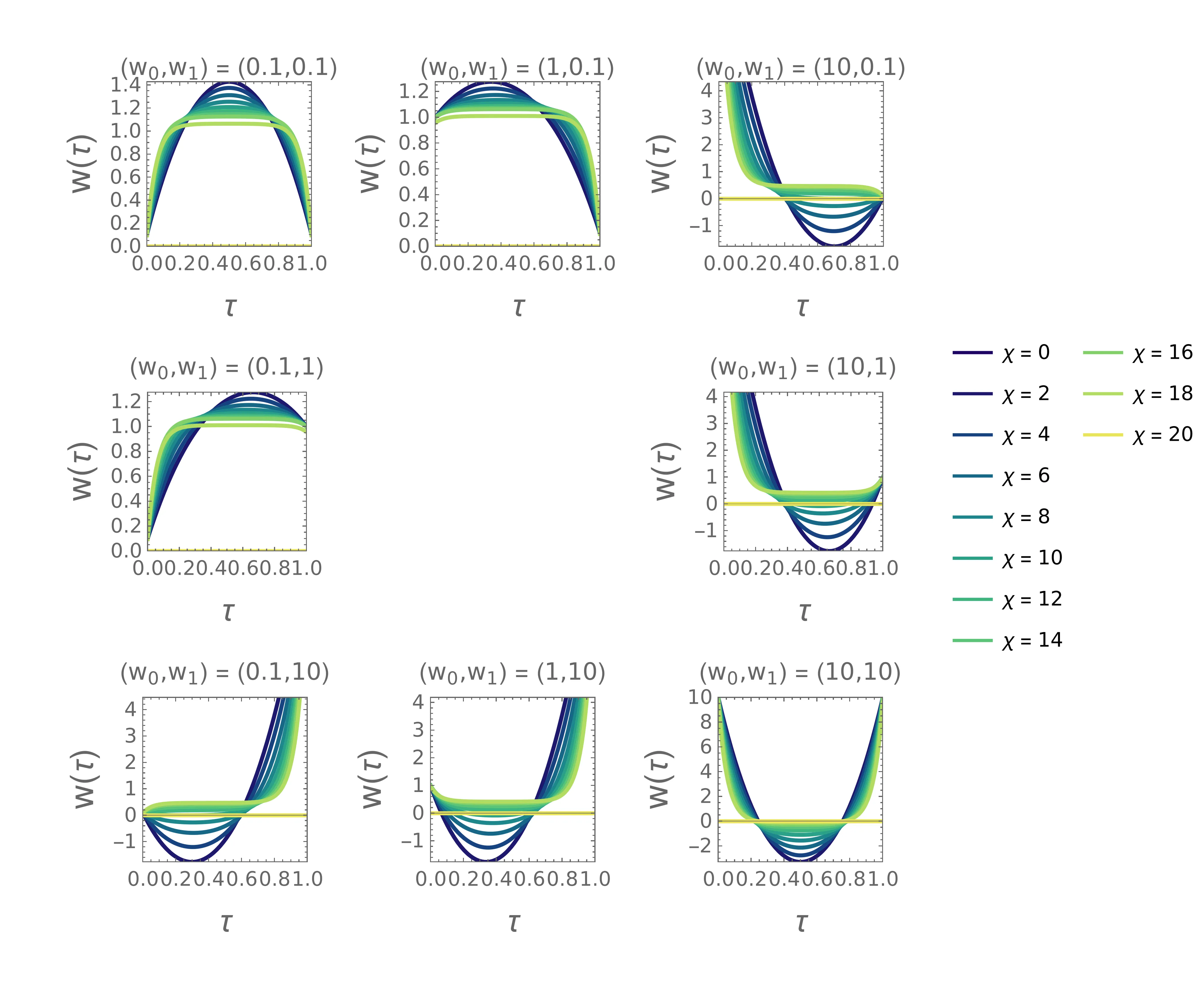
Poglejmo si poteke hitrosti, ki ustrezajo Lagrangianu s členom \(\chi^2 w^2\) še za zaprt robni pogoj (12). Temu ustreza rešitev (18) diferencialne enačbe \[\begin{aligned} w(\tau) &= \Lambda e^{-\chi\tau} \frac{e^\chi - e^{2\chi} - e^{\chi t} + e^{2\chi t} + e^{2\chi + \chi \tau} - e^{\chi + 2\chi \tau}}{2\chi^2(e^{2\chi} - 1)}. \nonumber \\ &+ e^{-\chi\tau} \frac{2w_0 e^{2\chi} - 2w_0 e^{2\chi\tau} -2 w_1 e^{\chi} + 2 w_1 \chi^2 e^{\chi + 2\chi\tau}}{2(e^{2\chi} - 1)}. \end{aligned}\] Ob upoštevanju vezi (1) dobimo za multiplikator \[\Lambda = \frac{2\chi^2 \left( \chi - w_0 \tanh \frac{\chi}{2} - w_1 \tanh \frac{chi}{2} \right)}{\chi - 2\tanh \frac{\chi}{2}}.\] Za kar nekaj vrednosti parametrov \((\chi^2, w_0, w_1)\) narišemo poteke na slikah 6, 7. Spet vidimo oblikovanje jasnih platojev za večje \(\chi\) (bolj močno kaznovana hitrost). Če bi kaznovali le hitrost (limita \(\chi \to \infty\)), bi optimalna oblika bila konstanta \(w = 1\), s koračnim skokom iz \(w_0\) na \(1\) pri \(\tau = 0\) in spet skokom iz \(w = 1\) na \(w_1\) pri \(\tau = 1\). Ta dva koračna skoka bi predstavljala dve delta funkciji za pospešek, ko je v Lagrangianu prisoten še \(\dot{w}^2\) člen, se to ne zgodi, temveč imamo namesto koračnega vseeno nek gladek prehod. Večji kot je \(\chi\), bolj oster je prehod in bolj podoben je koračnemu.

Preprečevanje overshootanja

Kot smo to že videli na slikah 2, 1, se dogaja, da avto pri nekem času \(\tau < 1\) pelje mimo semaforja, nato pa šele z vzvratno vožnjo pride na brezdimenzijsko razdaljo \(1\), da zadosti vezi (1). To bomo rešili tako, da bomo določili nekakšne meje na dovoljene parametre pri naši optimizaciji.

Overshoot z odprtim robnim pogojem

Iz slike 2 je vidno, da so vso poteki \(w(\tau)\) strogo monotoni (ali pa so konstanta). Tedaj je problem overshoot-anja semaforja rešen točno takrat, ko se izognemo negativnim hitrostim. Če za rešitev poteka za odprte robne pogoje (11) izračunamo diskriminanto, dobimo \[D = 3(3-4w_0+w_0^2),\] iz česar lahko določimo, da mora biti začetna hitrost² avtomobila navzgor omejena kot \[w_0 < w_0^{(max.)} = 3, \; \text{da preprečimo overshoot}.\]

Zaporedni semaforji

Zanimajo nas še načini vožnje skozi več zaporednih semaforjev. Takoj očitna možnost, ki se ponuja, so zlepljene rešitve za odprt robni pogoj ali zlepljene rešitve za zaprt robni pogoj, pri čemer je \(w_1\) (tako se vožnja ustali takoj po prvem odseku). Grafično ta dva poteka vidimo na 9 in 9.

Alternativno enačbo rešujemo tako, da robne pogoje določimo kar iz zveznosti in zvezne odvedljivosti. To dosežemo tako, da izberemo nek \(w_{00}\) in nek \(\dot{w}_{00}\), nato pa rešimo enačbo (5), apliciramo vez (1), nato pa začetne pogoje za naslednji odsek razberemo kar iz te funkcije na naslednjem robu \(\tau_n + 1\). Tako rešitev za \(w_0 = 2\) si pogledamo za nekaj različnih \(\dot{w}_{00}\) na sliki 10. Vidimo, da rešitev zna kar podivjati, razen za en ozek obseg parametrov.

Overshoot z zaprtim robnim pogojem

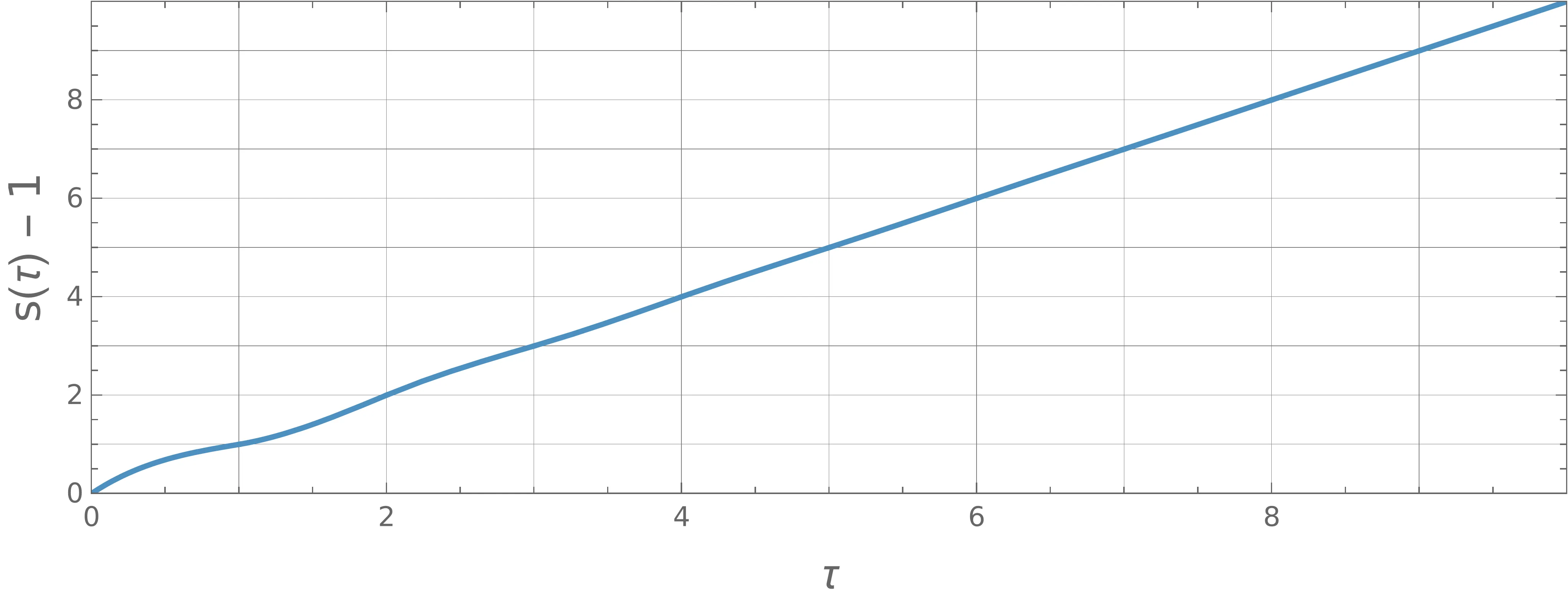
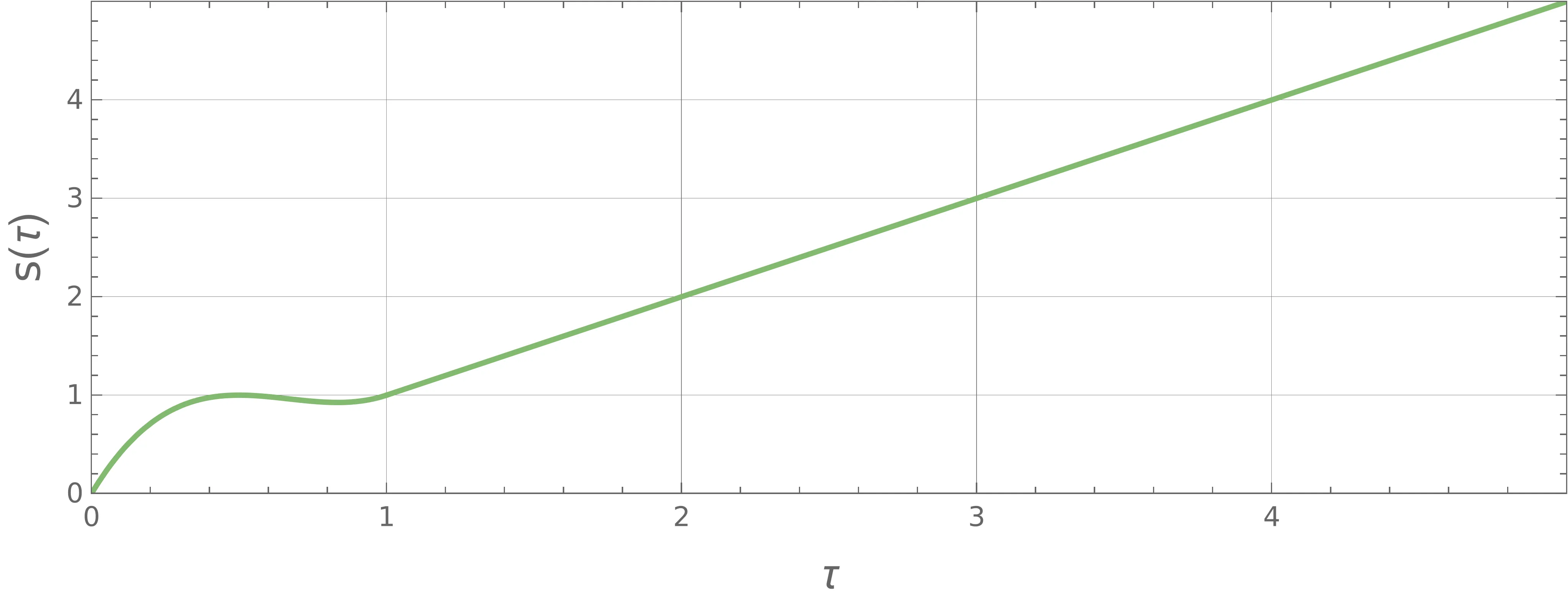
Pojav overshoot-anja se prav tako kot pri odprtih pogojih pojavi tudi pri zaprtih robnih pogojih (slika 1). A ker imamo zdaj dva prosta parametra \(w_0, w_1\) (namesto le enega), je določitev omejitve za preprečevanje overshoot-anja nekoliko težje. Ker poznamo potek hitrosti (13), lahko zapišemo tudi \(s(\tau)\), ki je nek polinom 3. stopnje. Ta polinom vedno poteka skozi točko \((\tau, s) = (1, 1)\), zato lahko njegovo obliko poenostavimo kot \[s(\tau) - 1 = (\tau - 1) Q(\tau),\] pri čemer je \(Q(\tau)\) nek kvadratični polinom \[Q(\tau) = 1 - t(1-w_0) - t^2(2 -w_0 - w_1),\] z ničlami tam, kjer je dosežena razdalja \(s(\tau) = 1\). Če je katera od teh dveh ničel \(\tau_{1,2}^{(Q)} \in (0, 1)\), je potek problematičen, saj semafor prevozimo pred \(\tau = 1\). Na sliki 11 je narisana diskriminanta \(Q(\tau)\) po parametrih \((w_0, w_1)\).

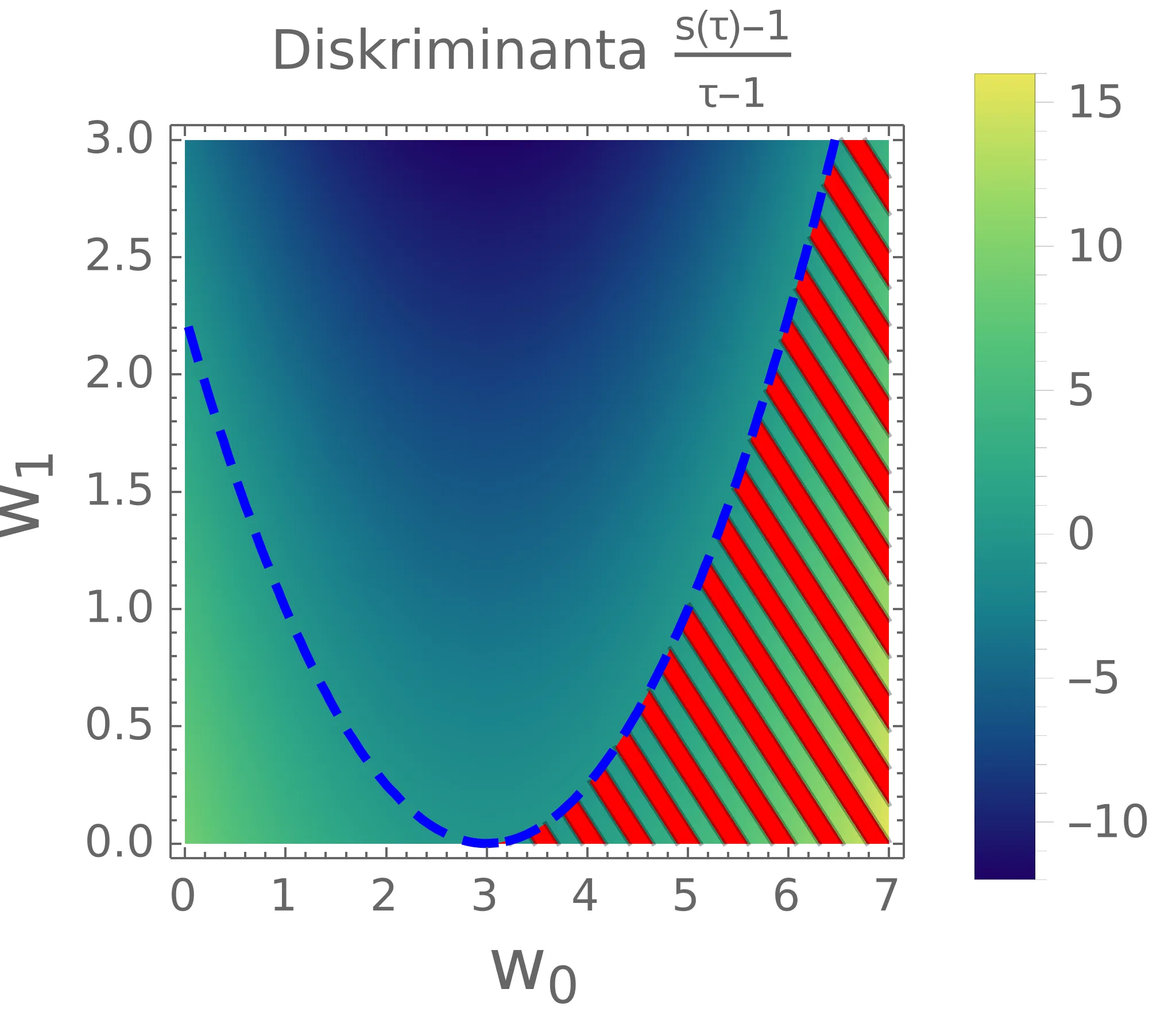
Zanima nas območje oz. pogoj za parametre, kjer je prisotno overshoot obnašanje. Prvi pogoj dobimo iz diskriminante \(Q(\tau)\) – če naj bo prisoten overshoot, bo \(Q(\tau)\) imel dve ničli. Pogoj, da ima \(Q(\tau)\) dve ničji, je \[w_1 < \frac{1}{4} \big(9 - 6w_0 + w_0^2\big).\] Potencialno območje je torej pod to krivuljo (modra črtkana parabola na sliki 11). Kot opisano na sliki 12, pa tudi območje \(w_0 < 3\) pod krivuljo ni problematično. Območje overshoot obnašanja je torej le območje, označeno z rdečo šrafirano na sliki 11. Komplement tega pogoja nam omogoči, da se overshoot-anju izognemo, sicer pod pogojem \[w_0 < 3 \quad \text{ali} \quad w_1 \ge \frac{1}{4} \big(9 - 6w_0 + w_0^2\big).\]