Sonar
Inverzni problem akustičnega loma v približku geometrijske akustike
Uvod
Zvok je v osnovi valoven pojav. Njegov matematični opis prestavlja valovna enačba
\[\left[ \nabla^2 - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right] u = 0,\]
ki je v splošnem izjemno bogata in opisuje tako mehanske snovne valove kot tudi elektromagnetno valovanje oz. svetlobo. Pogosto pa nas zanimajo le pogledi na določene lastnosti rešitev splošne valovne enačbe. Eden izmed takih aplikativnih pogledov najdemo v primeru širjenja zvočnih žarkov v oceanu ali Zemljini skorji (v nadaljevanju ocean). V oceanu se hitrost zvoka povečuje z globino. Akustični žarek, ki ga pošljemo navzdol v ocean pod nekim kotom, se zaradi naraščajoče hitrosti zvoka prej ali slej ukrivi navzgor in na neki razdalji od vira zopet doseže gladino.
Za neko prostorsko odvisno hitrost valovanja \(c(\mathbf{r})\) je propagacija začetne motnje določena z valovno enačbo – naloga določanje take propagacije je t. i. napovedni problem (ang. forward problem), saj iz določenega znanega vzročnega profila snovi izračunamo posledico.
Za uporabne namene pa nas pogosto zanima ravno nasprotna naloga, t. i. inverzni problem (ang. inverse problem). Pri inverznem problemu je profil snovi (vzrok za ukrivljanje žarka) neznan – znane so le meritve oz. posledica ukrivljanja žarka v snovi, npr. odvisnost dometa \(X(\vartheta_0)\) v odvisnosti od kota poslanega žarka \(\vartheta_0\). Ta naloga je v splošnem težja od napovedne. Kot bomo videli v nadaljevanju, obstoj rešitev ni nujno zagotovljen, za uspeh pa je potrebno kar nekaj predpostavk.
V nadaljevanju bomo opisani inverzni problem natančno formulirali v približku geometrijske optike in problem povezali z drugim matematično podobnim problemom. Preučili bomo probleme z obstojem rešitve in izpeljali rešitev v neproblematičnem primeru. Izpeljano rešitev in intuicijo pa bomo podkrepili tudi z nekaj numeričnimi primeri.
Formulacija problema
Geometrijska optika in žarkovna enačba
Problem širjenja akustičnih valov bomo obravnavali v približku geometrijske optike. Četudi sta zvok in svetloba različna pojava, ima njuna propagacija skupen opis v valovni enačbi. Približek geometrijske optike, kjer se svetloba širi vzdolž ravnih ali ukrivljenih žarkov, je pravzaprav bolj splošen.
V razvoju optike in akustike je valovna obravnava svetlobe in zvoka dobila jasno potrditev z uspešno pojasnitvijo uklona in interference. Šele precej kasneje pa se je pojavilo razumevanje, da je vsesplošno uporabna geometrijska optika le limitni primer valovne enačbe, ko gre valovna dolžina \(\lambda \to 0\). Takšna limita valovne enačbe se imenuje ikonalna enačba (ang. eikonal equation). Ikonalno enačbo lahko izpeljemo direktno iz Maxwellovih enačb [1, str. 117], v njej pa prepoznamo tudi 1. red WKB metode, uporabne tudi za reševanje Scrödingerjeve enačbe v kvantni mehaniki (glej npr. [2, str. 184]).
Osnovni vpogled nizkovalovnodolžinske limite pa je bil poznan dolgo pred formalnimi obravnavami valovne enačbe. Fermatovo načelo, ki ga je Pierre de Fermat zapisal že leta 1662, pravi, da valovanje1 med dvema točkama po mediju potuje po poti, za katero rabi najmanj časa [3]. Ob vpeljavi lomnega količnika \(n(\mathbf r) := \frac{c_0}{c(\mathbf r)}\) lahko Fermatovo načelo razumemo kot stacionarnost funkcionala
\[\delta \int_1^2 n(\mathbf r) \,\mathrm{d}s = 0.\]
Enačbo, ki opisuje pot posameznega žarka, lahko tedaj dobimo z uporabo Euler-Lagrangeve enačbe za variacijske probleme tega tipa, pri čemer je naš Lagrangian
\[\mathcal{L}(\mathbf{r}(t), \dot{\mathbf{r}}(t)) = n(\mathbf{r}) \cdot | \dot{\mathbf{r}} |\]
saj je \(\mathrm{d}s = |\dot{\mathbf{r}}| \mathrm{d}t\). Enačba za posamezno trajektorijo oz. žarek je tedaj
\[\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{r}}} \right) - \frac{\partial \mathcal{L}}{\partial \mathbf{r}} &= 0 \\ \frac{\mathrm{d}}{\mathrm{d}t} \left( n(\mathbf r) \cdot \frac{\dot{\mathbf{r}}}{|\dot{\mathbf{r}}|} \right) - \nabla n \cdot |\dot{\mathbf{r}}| &= 0, \end{aligned}\]
in če zdaj zopet uporabimo \(\mathrm{d}s = |\dot{\mathbf{r}}| \mathrm{d}t\), dobimo navadno diferencialno enačbo za žarek
\begin{equation}\frac{\mathrm{d}}{\mathrm{d}s} \left( n(\mathbf r) \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}s} \right) = \nabla n. \label{eq:ray-ode}\end{equation}
Širjenje v enodimenzionalnem profilu
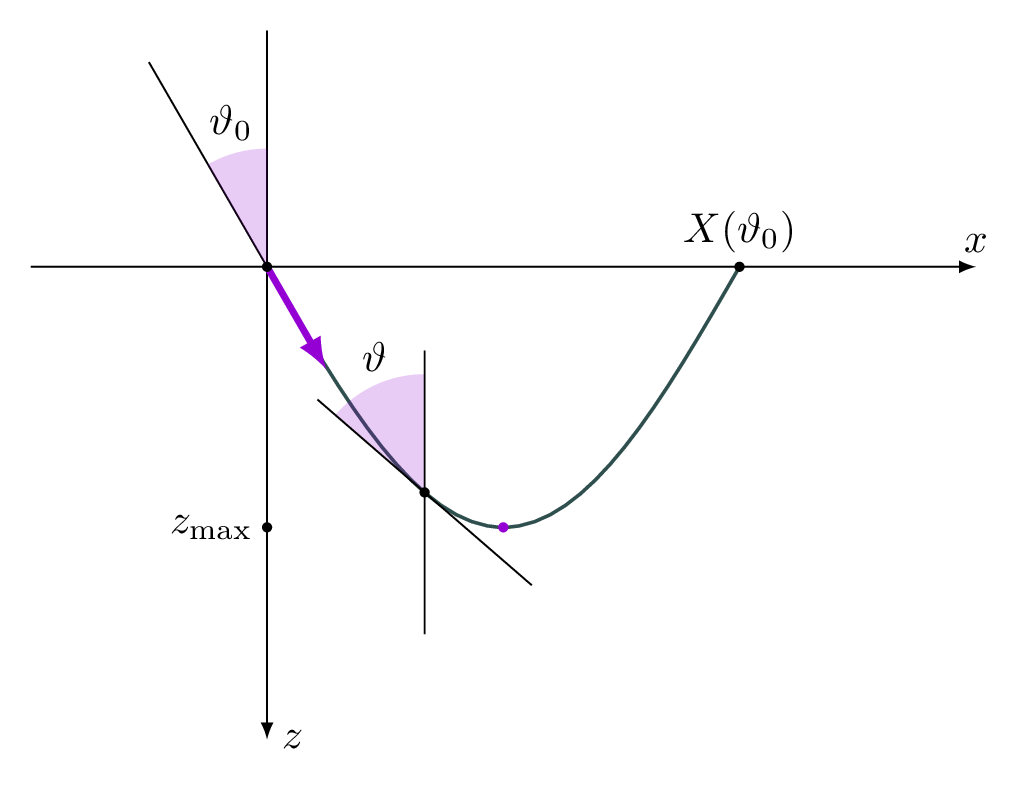
Žarkovna enačba (1) napoveduje trajektorijo žarka za neko začetno hitrost \(\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}s} \big\rvert_{t = 0} = (\cos \vartheta_0, -\sin \vartheta_0)\) iz izhodišča \(\mathbf{r} \big\rvert_{t = 0} = 0\). Taka trajektorija se bo ob zadostno naraščajoči hitrosti (oz. padajočem lomnemu količniku) zvoka ukrivila navzgor (slika 1) in ponovno dosegla gladino pri dometu \(X(\vartheta_0)\).
V nadaljevanju se bomo pri inverznem problemu omejili na enodimenzionalne profile hitrosti oz. lomnega količnika, ki se spreminjajo zgolj z globino oceana. Predstavljamo si ocean, ki ga sestavljajo tanke vodoravne plasti z različnimi lomnimi količniki. Iz oblike \(n(\mathbf r) = n(z)\) velja v \(x\)-komponenti žarkovne enačbe
\[\frac{\mathrm{d}}{\mathrm{d}s} \left( n(z) \frac{\mathrm{d}x}{\mathrm{d}s} \right) = \frac{\partial n}{\partial x} \equiv 0,\]
torej je na trajektoriji žarka količina \(n(z) \frac{\mathrm{d}x}{\mathrm{d}s} = n(z) \sin{\vartheta}\) konstantna. To konstanto, ki identificira posamezen žarek, imenujemo za žarkovno parameter \(p\)
\[p := n(z) \sin{\vartheta}.\]
Ohranitev žarkovnega parametra lahko razumemo tudi kot zvezno različico Snellovega lomnega zakona. Žarkovni parameter bo v parametrizaciji problema nadomestil začetni kot \(\vartheta_0\), tako da zdaj namesto odvisnosti dometa \(X(\vartheta_0)\) gledamo enakovredno odvisnost \(X(p)\). Žarkovna parameter je na gladini oceana, kjer je lomni količnik \(n(0) = n_0\), določen kot
\begin{equation}p = n_0 \sin{\vartheta_0}. \label{eq:initial}\end{equation}
Napovedni model
Preden se lotimo inverznega problema, moramo zapisati napovedni model. V našem primeru je to predpis, ki določenemu znanemu profilu lomnega količnika \(n(z)\) pripiše napovedno funkcijo dometa \(X(\vartheta_0)\).
Ker se žarkovni parameter \(p\) ohranja vzdolž trajektorije, velja \(\sin\vartheta = p / n(z)\) in po preprosti trigonometrični identiteti zapišemo
\[\frac{\mathrm{d}x}{\mathrm{d}z} \equiv \tan \vartheta = \frac{p / n(z)}{\sqrt{1 - \big( p/n(z) \big)^2}}.\]
Iz simetrijskih razlogov je jasno, da je trajektorija posameznega žarka simetrična glede na točko, pri kateri žarek doseže največjo globino \(h\) (glej skico 1). Žarek torej v navpični smeri prepotuje od \(z = 0\) do \(z = h\), hkrati pa v horizontalni razdalji prepotuje ravno polovico dometa \(X/2\). Zato lahko domet \(X\), v katerem žarek ponovno doseže gladino, zapišemo kot
\[X = 2 \int_0^h \,\mathrm{d}x = 2p \int_0^h \frac{\mathrm{d}z}{\sqrt{n(z)^2 - p^2}}.\]
S formalno2 uvedbo nove spremenljivke \(u = n_0^2 - n(z)^2\) in zgornje meje \(P := n_0 - n(h)^2\) lahko to zapišemo tudi kot
\begin{equation}\frac{X(P)}{2p} = \int_{0}^P \frac{\left[ -\frac{1}{2n n'(z)} \right]_u}{\sqrt{P - u}} \,\mathrm{d}u, \label{eq:forward0}\end{equation}
Pri tem smo zgornjo mejo integrala \(P = n_0^2 - n(h)^2\) uvedli kot nov parameter. Ta je določen ravno z žarkovnim parametrom, ko velja, da je na dnu trajektorije, pri globini \(h\), lokalni kot žarka \(\theta = \frac{\pi}{2}\). Iz ohranitve žarkovnega parametra \(p = n(h) \sin \frac{\pi}{2}\) tedaj velja
\[n(h) = p \qquad P = n_0^2 - p^2\]
in nova zgornja meja integrala in parameter za napovedno funkcijo dometa je po (2) tedaj
\[P = n_0^2 \cos^2 \vartheta_0.\]
Kot na skici 1 je v intuitivni predstavi trajektoriji žarka očitno, da je lokalni kot žarka na dnu trajektorije ravno \(\frac{\pi}{2}\). A formalno je za to potrebna zvezno odvedljiva trajektorija. Povsem preprosto si prestavljamo protiprimer, kjer se žarek popolno odbije od stika plasti, na katerem ima lomni količnik nezvezen skok. Pri odboju od takega stika je tudi sprememba smeri žarka ne-infinitezimalna in lokalni kot na dnu trajektorije ni definiran.
Predpostavka. Profil lomnega količnika \(n(z)\) je (odsekoma) zvezna funkcija.
V predpostavko smo dodali možno relaksacijo, da je lomni količnik le odsekoma zvezen. Tedaj imamo na nezveznih skokih prisotne tudi odboje, ki jih ne opisuje geometrijska optika, razen v primeru popolnega odboja. V nadaljevanju diskusije je privzeto, da taki odboji niso prisotni v sliki napovedne funkcije \(X(P)\) – za nas je pomembno le, da je dno trajektorije žarka v enem izmed zveznih odsekov.
S to predpostavko lahko na zvezno odvedljivost trajektorije sklepamo iz žarkovne enačbe v zveznem profilu \(n(z)\)
\[\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}s} \left( n(z) \frac{\mathrm{d}z}{\mathrm{d}s} \right) &= \frac{\partial n}{\partial z} \\ n(z) \frac{\mathrm{d}z}{\mathrm{d}s} &= \int_0^z \left[ \frac{\partial n}{\partial z} \right]_{z'} \left[ \frac{\mathrm{d}z}{\mathrm{d}s} \right]_{z'} \,\mathrm{d}z'. \end{aligned}\]
Ker sta v integrandu na desni strani odvoda dveh zveznih funkcij, je tudi leva stran zvezna, kar pa neposredno pomeni zvezno odvedljivost trajektorije \(z(s)\). Tako argument o parabolični obliki dna trajektorije ohrani veljavnost.
Napovedna funkcija \(\widetilde{X}(P)\) je tedaj izražen kompaktno kot integral
\begin{equation}\widetilde{X}(P) = \int_{0}^P \frac{F(u)}{\sqrt{P - u}} \,\mathrm{d}u, \label{eq:forward}\end{equation}
pri čemer smo uvedli modificirano napovedno funkcijo kot
\[\widetilde{X}(P) = \frac{X(P)}{2p} = \frac{X(P) / 2}{\sqrt{n_0^2 - P}}\]
v integrandu pa funkcijo
\begin{equation}F(u) := \left[ -\frac{1}{2nn'(z)} \right]_u = \left[ \frac{\mathrm{d}z}{\mathrm{d}u} \right]_u, \label{eq:forward-F}\end{equation}
saj je \(\frac{\mathrm{d}u}{\mathrm{d}n} = -2n\) odkar smo uvedli novo spremenljivko \(u = n_0^2 - n(z)^2\)
\[-\frac{1}{2nn'(z)} = \left( \frac{-1}{2n} \right) \frac{\mathrm{d}z}{\mathrm{d}n} = \left( \frac{-1}{2n} \right) \frac{\mathrm{d}u}{\mathrm{d}n} \frac{\mathrm{d}z}{\mathrm{d}u} = \frac{\mathrm{d}z}{\mathrm{d}u}.\]
Abelov problem

Za boljše razumevanje problema bomo predstavili podoben inverzni problem iz mehanike, ki ga je v svojem zgodnjem delu predstavil Abel [4, str. 6]. Gre za inverzni problem, pri katerem želimo izračunati neznano obliko klančine, po kateri se kotali objekt. Vhodni podatek so znani časi kotaljenja po \(T(h)\) kot funkcija začetnih višin \(h\) (glej sliko 2). Če je začetna višina \(h\), lahko iz ohranitve energije neposredno zapišemo, da hitrost narašča kot
\[\frac{\mathrm{d}s}{\mathrm{d}t} \Big\rvert_z = \sqrt{2g(h - z)},\]
ko se krogla skotali od \(z = h\) do \(z = 0\). Tedaj lahko zapišemo spremembo časa, ki preteče ob majhnem koraku \(\mathrm{d}z\) v navpičnem pomikanju krogle
\[\mathrm{d}t = \frac{\mathrm{d}s}{\sqrt{2g(h - z)}} = \frac{\left[ \frac{\mathrm{d}s}{\mathrm{d}z} \right] \mathrm{d}z}{\sqrt{2g(h - z)}}\]
Celoten čas kotaljenja od začetne višine \(h\) do dna je tedaj izražen kot integral
\begin{equation}T(h) = \int_0^h \frac{F(z)}{\sqrt{h - z}} \,\mathrm{d}z, \label{eq:abel-forward}\end{equation}
pri čemer je funkcija v integrandu
\begin{equation}F(z) = \frac{-1}{\sqrt{2g}} \left[ \frac{\mathrm{d}s}{\mathrm{d}z} \right]_z \label{eq:abel-forward-F}\end{equation}
Vidimo, da je napovedna formula Abelovega problema (6) povsem enake oblike kot napovedna formula (4) za problem širjenja žarkov v oceanu. Za rešitev obeh inverznih problemov potrebujemo rešiti isto integralsko enačbo enake oblike, poimenovano po Abelu. Za širjenje žarkov predstavlja \(u = n_0^2 - n(z)^2\) analog obliki klančine \(x(z)\) v Abelovem mehanskem problemu. S to analogijo si bomo v nadaljevanju pomagali pri intuitivnem razumevanju obstoja rešitev za inverzni problem.
| Abelov problem | Širjenje akustičnih žarkov, \(u = n_0^2 - n(z)^2\) |
|---|---|
| napoved \(T(h) = \int_0^h \frac{F(z) \,\mathrm{d}z}{\sqrt{h - z}}\) | \(\widetilde{X}(P) = \int_{0}^P \frac{F(u) \,\mathrm{d}u}{\sqrt{P - u}}\) |
| \(F(z) := \frac{-1}{\sqrt{2g}} \left[ \frac{\mathrm{d}s}{\mathrm{d}z} \right]_z\) | \(F(u) := \left[ \frac{\mathrm{d}z}{\mathrm{d}u} \right]_u \quad \widetilde{X}(P) := \frac{X(P) / 2}{\sqrt{n_0^2 - P}}\) |
| inverz \(F(z) = \frac{1}{\pi} \frac{\mathrm{d}}{\mathrm{d}z} \int_0^z \frac{T(h) \,\mathrm{d}h}{\sqrt{z - h}}\) | \(F(u) = \frac{1}{\pi} \frac{\mathrm{d}}{\mathrm{d}u} \int_0^u \frac{\widetilde{X}(P) \,\mathrm{d}P}{\sqrt{u - P}}\) |
| \(s(z) = \mathcal{S}_\mathrm{total} - \frac{\sqrt{2g}}{\pi} \int_0^z \frac{T(h) \,\mathrm{d}h}{\sqrt{z - h}}\) | \(z(u) = \frac{1}{\pi} \int_0^u \frac{\widetilde{X}(P) \,\mathrm{d}P}{\sqrt{u - P}} \quad z(n) = \frac{1}{\pi} \int_{0}^{[X]_{p=n}} \mathop{\mathrm{arcosh}}\left( \frac{p}{n} \right) \,[\mathrm{d}X]_p\) |
Bôcher predstavi metodo, po kateri je Abelovo integralsko enačbo izvorno rešil Louville. Poda potrebne in zadostne pogoje (Bôcherjeve pogoje v nadaljevanju), da ima integralska enačba (6) zvezno rešitev [4, str. 9]. Če je \(T(0) = 0\), napovedna funkcija \(T(h)\) pa zvezna in odsekoma zvezno odvedljiva, ima integralska enačba (6) zvezno rešitev
\begin{equation}F(z) = \frac{1}{\pi} \frac{\mathrm{d}}{\mathrm{d}z} \int_0^z \frac{T(h)}{\sqrt{z - h}} \,\mathrm{d}h, \label{eq:bocher-inverse}\end{equation}
trivialno pa je uvideti, da je tedaj oblika klanca podana v implicitni obliki kot
\[\quad s(z) = \mathcal{S}_\mathrm{total} - \frac{\sqrt{2g}}{\pi} \int_0^z \frac{T(h) \,\mathrm{d}h}{\sqrt{z - h}} .\]
V nadaljevanju bomo podobno integralsko enačbo rešili na drugačen način, sprostili pa bomo tudi nekatere izmed Bôcherjevih pogojev, ki niso nujno potrebne za rešitev problema. Predpostavke kot je npr. zveznost napovedne funkcije \(T(h)\), pa bomo poskusili bolj intuitivno razumeti kot posledice opazovanega sistema, ne zgolj kot lastnost napovedne funkcije.
Matematična diskusija
Abelova integralska transformacija
Integralsko enačbo Abelovega tipa, kakršni sta napovedni formuli (6) in (4), bomo rešili z uporabo konvolucije. Prvo bomo obravnavali sorodno integralsko transformacijo, t. i. Abelovo transformacijo3 (glej [6, str. 351])
\begin{equation}F_\mathrm{A}(\mathcal{P}) = \int_\mathcal{P}^\infty \frac{F(\rho) \,\mathrm{d}\rho}{\sqrt{\rho - \mathcal{P}}}. \label{eq:cousin}\end{equation}
Želimo si izračunati inverz take transformacije, tako da lahko na podlagi podanega \(F_\mathrm{A}(\mathcal{P})\) izračunamo funkcijo \(F(\rho)\). Za to potrebujemo rešiti integralsko enačbo (9). Ključen korak, ki to omogoči, je ugotovitev, da lahko spodnjo mejo integrala odstranimo, če v integrandu umetno dodamo Heaviside koračno funkcijo \(\theta(\rho - \mathcal{P})\)
\begin{equation}\int_\mathcal{P}^\infty \frac{F(\rho) \,\mathrm{d}\rho}{\sqrt{\rho - \mathcal{P}}} = \int_{-\infty}^\infty \frac{\theta(\rho - \mathcal{P})}{\sqrt{\rho - \mathcal{P}}} \,F(\rho) \,\mathrm{d}\rho = \int_{-\infty}^\infty K(\mathcal{P} - \rho) \, F(\rho) \,\mathrm{d}\rho, \label{eq:conv}\end{equation}
pri čemer smo v integrandu uvedli funkcijo \(K\) kot
\begin{equation}K(x) := \frac{\theta(-x)}{\sqrt{-x}}. \label{eq:kernel}\end{equation}
Iz integrala na desni strani (10) je takoj jasno, da imamo opravka s konvolucijo, kjer funkcija \(K\) nastopa kot konvolucijsko jedro. Abelovo transformiranko lahko torej zapišemo preprosto kot
\[F_\mathrm{A} = K \ast F.\]
Z uporabo konvolucijskega izreka lahko to enačbo rešimo v frekvenčni domeni. Za Fourierovo transformacijo, definirano kot
\[\widehat{f}(\xi) := \int f(x)\,e^{-i2\pi \xi x} \,\mathrm{d}x \qquad f(x) = \int \widehat{f}(\xi)\,e^{i2\pi \xi x} \,\mathrm{d}\xi,\]
se integralska enačba v frekvenčni domeni poenostavi v algebraično enačbo \(\widehat{F}_\mathrm{A}(\xi) = \widehat{K}(\xi)\,\widehat{F}(\xi)\), katere rešitev je
\[\widehat{F}(\xi) = \frac{ \widehat{F}_\mathrm{A}(\xi)}{ \widehat{K}(\xi) }\]
Izračun Fourierove transformacije za funkcijo jedra ni ključnega pomena za razumevanje glavnega argumenta, zato ga bomo izpustili4. Tu brez računa uporabimo rezultat
\[\widehat{K}(\xi) = \frac{1}{\sqrt{-2i \xi}}.\]
V frekvenčni domeni je tedaj rešitev \(\widehat{F}(\xi)\) preprosto
\[\widehat{F}(\xi) = \sqrt{-2i \xi}\,\widehat{F}_\mathrm{A}(\xi) = -\frac{1}{\pi} \frac{1}{\sqrt{-2i \xi}}\,\widehat{F_\mathrm{A}^\prime}(\xi) \notag \\\]
pri čemer smo pri drugi enakosti uporabili dejstvo, da je v frekvenčni domeni \(\widehat{F_\mathrm{A}^\prime} = -i2\pi \xi \, \widehat{F_\mathrm{A}}\), pri čemer je \(F_\mathrm{A}^\prime(\mathcal{P})\) odvod po \(\mathcal P\), ki je očitno iz definicije Fourierove transformacije. V frekvenčni domeni imamo torej rešitev
\[\widehat{F}(\xi) = -\frac{1}{\pi} \widehat{K}(\xi)\,\widehat{F_\mathrm{A}^\prime}(\xi),\]
in če jo zopet Fourierovo transformiramo, dobimo kot rešitev \(F\) konvolucijo
\begin{equation}F = -\frac{1}{\pi} K \ast F_\mathrm{A}^\prime \label{eq:conv-solution}\end{equation}
kar pa lahko spet zapišemo drugače kot
\[\begin{aligned} F(\rho) &= -\frac{1}{\pi} \int_{-\infty}^{\infty} K(\rho - \mathcal{P}) \, F_\mathrm{A}^\prime(\mathcal{P}) \,\mathrm{d}\mathcal{P} \\ &= -\frac{1}{\pi} \int_{-\infty}^{\infty} \frac{\theta(\mathcal{P} - \rho)}{\sqrt{\mathcal{P} - \rho}} \, F_\mathrm{A}^\prime(\mathcal{P}) \,\mathrm{d}\mathcal{P}, \end{aligned}\]
če pa upoštevamo še dejstvo, da je integrand zaradi Heavisideove funkcije neničelen le za \(P > \rho\), dobimo rešitev integralne enačbe (9) oz. formula za inverz Abelove transformacije
\begin{equation}F(\rho) = -\frac{1}{\pi} \int_{\rho}^{\infty} \frac{F_\mathrm{A}^\prime(\mathcal{P})}{\sqrt{\mathcal{P} - \rho}} \,\mathrm{d}\mathcal{P}. \label{eq:abel-inverse}\end{equation}
Rešitev Abelove integralske enačbe z Abelovo transformacijo
Abelovo transformacijo in njen inverz (13) bomo zdaj uporabili za rešitev Abelove integralske enačbe (6). Z uvedbo nove spremenljivke \(\rho = 1/z\) in oznake \(\mathcal{P} = 1/h\) lahko napovedno enačbo Abelovega problema zapišemo kot
\[\begin{aligned} T(h) &= \int_0^h \frac{F(z)}{\sqrt{h - z}} \,\mathrm{d}z = \int_0^h \frac{F(z)}{\sqrt{\frac{1}{z} - \frac{1}{h}}} \,\frac{\mathrm{d}z}{\sqrt{zh}} \\ T(h) &= \int_\mathcal{P}^\infty \frac{\frac{1}{\sqrt{h}} \left[ z^{\frac{3}{2}} F(z) \right]_\rho}{\sqrt{\rho - \mathcal{P}}} \,\mathrm{d}\rho, \end{aligned}\]
Če enakost množimo z \(\sqrt{h}\), lahko zapišemo
\[\left[ \sqrt{h}\, T(h) \right]_\mathcal{P} = \int_\mathcal{P}^\infty \frac{\left[ z^{\frac{3}{2}} F(z) \right]_\rho}{\sqrt{\rho - \mathcal{P}}} \,\mathrm{d}\rho,\]
kar pomeni, da je \(G_\mathrm{A}(\mathcal{P}) := \left[ \sqrt{h}\, T(h) \right]_\mathcal{P}\) Abelova transformiranka funkcije \(G(\rho) := \left[ z^{\frac{3}{2}} F(z) \right]_\rho\). Ker poznamo transformiranko \(G_\mathrm{A}\), lahko preko formule (13) izračunamo njen inverz
\[G(\rho) = \left[ z^{\frac{3}{2}} F(z) \right]_\rho = -\frac{1}{\pi} \int_\mathcal{\rho}^\infty \frac{ \frac{\mathrm{d}}{\mathrm{d}{\mathcal{P}}} \left[ \sqrt{h}\, T(h) \right]_\mathcal{P}}{\sqrt{\mathcal{P} - \rho}} \,\mathrm{d}h.\]
Zgornji izraz je, čeprav nekoliko nerodno zapisan, rešitev Abelove integralske enačbe. Bolj jasno postane, če kot spremenljivko nazaj uvedemo oznako \(h = 1/\mathcal{P}\), vključno z novo spodnjo mejo \(z = 1/\rho\)
\[z^{\frac{3}{2}} F(z) = -\frac{1}{\pi} \int_\mathcal{\rho}^\infty \frac{ \frac{\mathrm{d}}{\mathrm{d}{h}} \left( \sqrt{h}\, T(h) \right) \frac{\mathrm{d}h}{\mathrm{d}\mathcal{P}} }{\sqrt{\mathcal{P} - \rho}} \,\mathrm{d}\mathcal{P} = -\frac{1}{\pi} \int_z^0 \frac{ \frac{\mathrm{d}}{\mathrm{d}{h}} \left( \sqrt{h}\, T(h) \right) \sqrt{hz} }{\sqrt{z - h}} \,\mathrm{d}h.\]
Rešitev Abelove integralske enačbe (6), s tem pa tudi enakovredne enačbe (4), je podana z izrazom
\begin{equation}F(z) = \frac{1}{\pi z} \int_0^z \frac{ \frac{\mathrm{d}}{\mathrm{d}{h}} \left( \sqrt{h}\, T(h) \right) \sqrt{h} }{\sqrt{z - h}} \,\mathrm{d}h. \label{eq:ugly-solution}\end{equation}
Zapis rešitve v standardni obliki
Izraz (14) je rešitev Abelove enačbe. V literaturi pa je rešitev tipično zapisana v nekoliko drugačni obliki (8). Če predpostavimo prvega izmed Bôcherjevih pogojev, t. j.
Prvi Bôcherjev pogoj. Napovedna funkcija \(T(h)\) je v točki 0 definirana in je enaka \(0\),
potem lahko integral (14) preoblikujemo. Ker je v integrandu imenovalec \(\sqrt{z - h}\), ki ni definiran na zgornji meji \(h = z\), moramo izraz razumeti v posplošenem smislu
\[\lim_{y_n(z) \to z} \frac{1}{\pi y_n(z)} \int_0^{y_n(z)} \frac{ \frac{\mathrm{d}}{\mathrm{d}{h}} \left( \sqrt{h}\, T(h) \right) \sqrt{h} }{\sqrt{z - h}} \,\mathrm{d}h,\]
pri čemer je \(y_n(z)\) zaporedje zvezno odvedljivih funkcij, ki konvergira k \(y_n(z) \mapsto z\), in za katerega za vsak \(z\) velja \(y_n(z) < z\). Tedaj lahko znotraj limite integriramo po delih
\[\begin{aligned} \lim_{y_n(z) \to z} \frac{1}{\pi y} \int_0^{y_n(z)} \frac{ \frac{\mathrm{d}}{\mathrm{d}{h}} \left( \sqrt{h}\, T(h) \right) \sqrt{h} }{\sqrt{z - h}} \,\mathrm{d}h &= \lim_{y_n(z) \to z} \frac{1}{\pi} \left\{ \frac{h T(h)}{\sqrt{z - h}} \Big\rvert_{h=0}^{h=y_n(z)} + \cancelto{1}{ \frac{z}{y_n} } \int_0^{y_n(z)} \frac{T(h)}{ 2(z - h)^{\frac{3}{2}} } \,\mathrm{d}h \right\} \\ &= \lim_{y_n(z) \to z} \frac{1}{\pi} \left\{ \frac{y_n T(y_n)}{\sqrt{z - y_n}} \cdot \frac{\mathrm{d}y_n}{\mathrm{d}z} \cancelto{1}{ \frac{\mathrm{d}z}{\mathrm{d}y_n} } + \int_0^{y_n(z)} \frac{\partial}{\partial z} \left( \frac{T(h)}{ \sqrt{z - h} } \right) \,\mathrm{d}h \right\} \\ &= \lim_{y_n(z) \to z} \frac{1}{\pi} \left\{ \frac{\mathrm{d}}{\mathrm{d}z} \int_0^{y_n(z)} \frac{T(h)}{ \sqrt{z - h} } \,\mathrm{d}h \right\}, \end{aligned}\]
pri čemer smo uporabili pravila za računanje z limitami, pri zadnji enakosti pa uporabili Leibnizovo pravilo za odvajanje po parametru. Izraz za rešitev smo torej prevedli na obliko
\begin{equation}F(z) = \lim_{y_n(z) \to z} \frac{1}{\pi} \left\{ \frac{\mathrm{d}}{\mathrm{d}z} \int_0^{y_n(z)} \frac{T(h)}{ \sqrt{z - h} } \,\mathrm{d}h. \right\} \label{eq:lim-diff}\end{equation}
Zdaj nas zanima še, ali lahko zamenjamo odvod in limito oz. pod kakšnim pogojem to lahko naredimo. Če gledamo limito kot zaporedje funkcij \(\frac{\mathrm{d}g_n}{\mathrm{d}z}\), pri čemer je
\[g_n(z) := \int_0^{y_n(z)} \frac{T(h)}{ \sqrt{z - h} } \,\mathrm{d}h,\]
je za menjavo limite in odvoda zadostno, da integral \(\int_0^{z} \frac{T(h)}{ \sqrt{z - h} } \,\mathrm{d}h\) konvergira uniformno \(\forall z\). Za to je dovolj, da je \(T(h)\) omejen v neki okolici \(h \in (0, \delta]\), drugje je \(T(h)\) omejen ali pa ima končno število polov stopnje \(\gamma < \frac{1}{2}\). V takem primeru lahko preostanek \(\varepsilon(z) = \int_0^{z} \frac{T(h)}{ \sqrt{z - h} } \,\mathrm{d}h - \int_0^{y_n(z)} \frac{T(h)}{ \sqrt{z - h} } \,\mathrm{d}h\) omejimo z uniformnim \(\varepsilon\) integracijskim preostankom tistega najmočnejšega izmed polov.
Tedaj \(g_n(z)\) kot funkcijsko zaporedje uniformno konvergira k funkciji
\[g(z) := \int_0^{z} \frac{T(h)}{ \sqrt{z - h} } \,\mathrm{d}h,\]
zaporedje \(\frac{\mathrm{d}g_n}{\mathrm{d}z}\) pa konvergira k
\[F(z) = \lim_{y_n(z) \to z} \frac{\mathrm{d}g_n}{\mathrm{d}z} = \frac{\mathrm{d}g}{\mathrm{d}z}.\]
Odvod in limito v (15) lahko torej zamenjamo in zapišemo rešitev Abelove integralske enačbe v standardni obliki, ki jo najdemo v večini literature
\begin{equation}F(z) = \frac{1}{\pi} \frac{\mathrm{d}}{\mathrm{d}z} \int_0^{z} \frac{T(h)}{ \sqrt{z - h} } \,\mathrm{d}h. \label{eq:nice-solution}\end{equation}
Zveznost rešitev
Poleg prvega Bôcherjevega pogoja, ki smo ga delno uporabili, je za zveznost rešitve \(F(z)\) potreben še en pogoj
Tretji Bôcherjev pogoj. Napovedna funkcija \(T(h)\) je odsekoma zvezno odvedljiva,
Da to res vodi do zvezne rešitve \(F(z)\), lahko zelo hitro preverimo, če pogledamo rešitev v obliki
\[F(z) = \frac{1}{\pi z} \int_0^z \frac{ \frac{\mathrm{d}}{\mathrm{d}{h}} \left( \sqrt{h}\, T(h) \right) \sqrt{h} }{\sqrt{z - h}} \,\mathrm{d}h = \frac{1}{\pi z} \int_0^z \frac{ -\frac{1}{2} T(h) + hT'(h) }{\sqrt{z - h}} \,\mathrm{d}h,\]
kjer je v integrandu prisoten \(T'(h)\). Če je ta odvod odsekoma zvezen, je očitno, da je zvezna tudi rešitev \(F(z)\).
Obstoj in oblika rešitev
Z inverzijskim predpisom (16) smo zdaj rešili tako Abelov problem kot tudi inverzni problem širjenja žarkov (4) (za primerjavo problemov glej povzetek v tabeli 1).
\[F(u) = \frac{1}{\pi} \frac{\mathrm{d}}{\mathrm{d}z} \int_0^u \frac{\widetilde{X}(P)}{\sqrt{u - P}} \,\mathrm{d}P.\]
Ker je \(F(u)\) v primeru širjenja žarkov enak \(F(u) := \left[ \frac{\mathrm{d}z}{\mathrm{d}u} \right]_u\), lahko preprosto zapišemo \(u = n_0^2 - n(z)\) kot funkcijo \(z\)
\[z(u) = \frac{1}{\pi} \int_0^u \frac{\widetilde{X}(P)}{\sqrt{u - P}} \,\mathrm{d}P.\]
Še nekaj več bomo povedali o obstoju rešitev. Kriterije bomo namenoma obravnavali na način, ki je intuitivno povezan s problemom, ne le kot formalne matematične predpostavke.
Injektivnost \(n(z)\)
V razdelku 4 smo v obravnavi Abelove integralske enačbe razjasnili pomen prvega in tretjega Bôcherjevega pogoja. Ostaja nam še en
Tretji Bôcherjev pogoj. Napovedna funkcija \(T(h)\) je zvezna.
Ta Bôcherjev pogoj smo v diskusiji do sedaj namenoma izpustili. Pravzaprav ga v naši poti do rešitve sploh nismo potrebovali, nadomestili pa ga bomo s pogojem, ki se nanaša na profil \(n(z)\), ne na napovedno funkcijo \(X(P)\). To predpostavko smo tiho privzeli v uvedbi nove spremenljivke, ko smo zapisali napovedni integral (3).
Nadomestek 2. Bôcherjevega pogoja. Profil5 \(n(z)\) je padajoča injektivna funkcija. Če je \(n(z)\) padajoča injektivna funkcija le na nekem intervalu \([0, z_c]\), lahko rekonstruiramo profil v obliki \(z(n)\) le za \(n \in [n_0, n(z_c)]\).
Pogoj injektivnosti je v primeru zveznega profila ekvivalenten strogi monotonosti funkcije povsod, razen morda v končnemu številu točk.
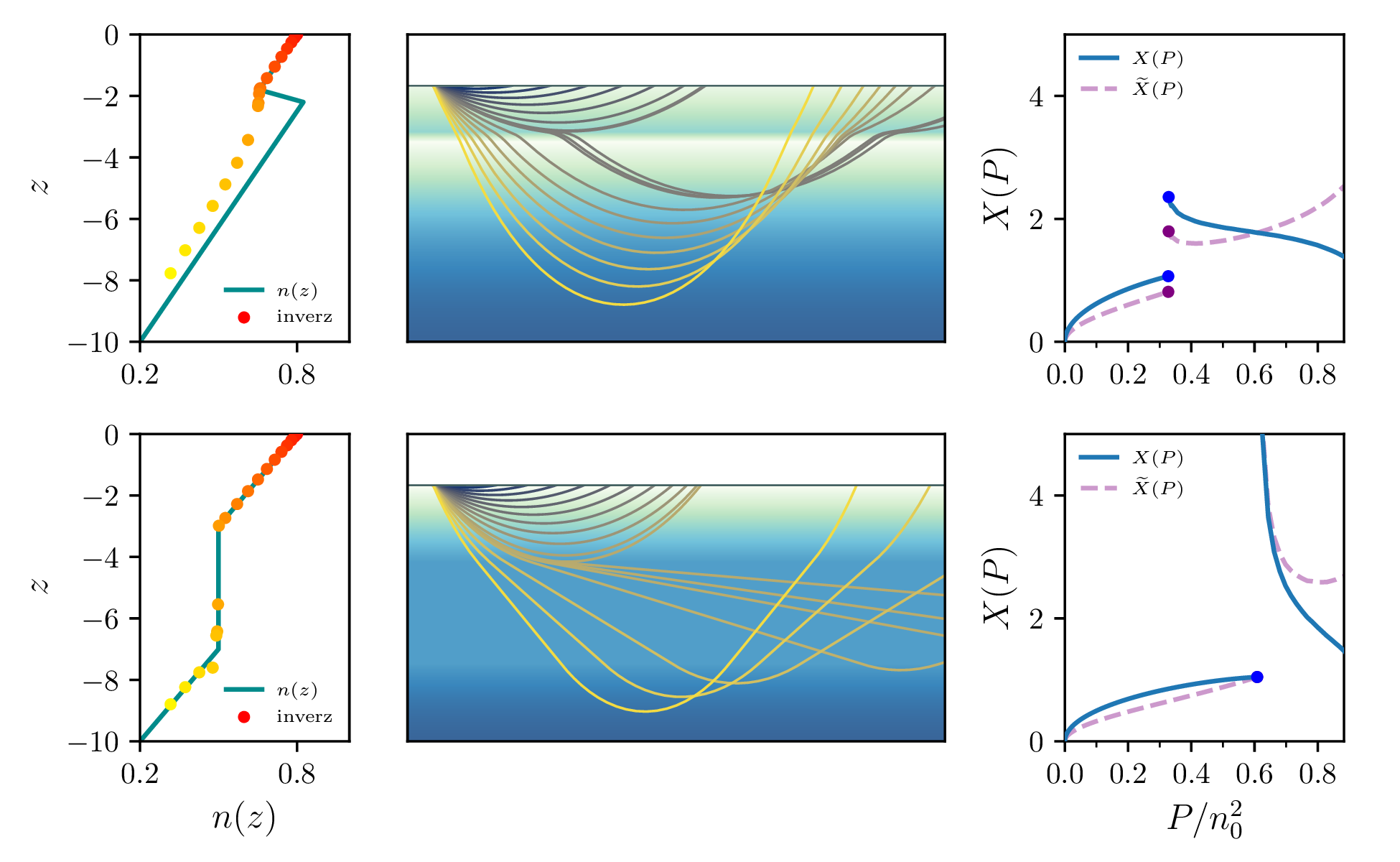
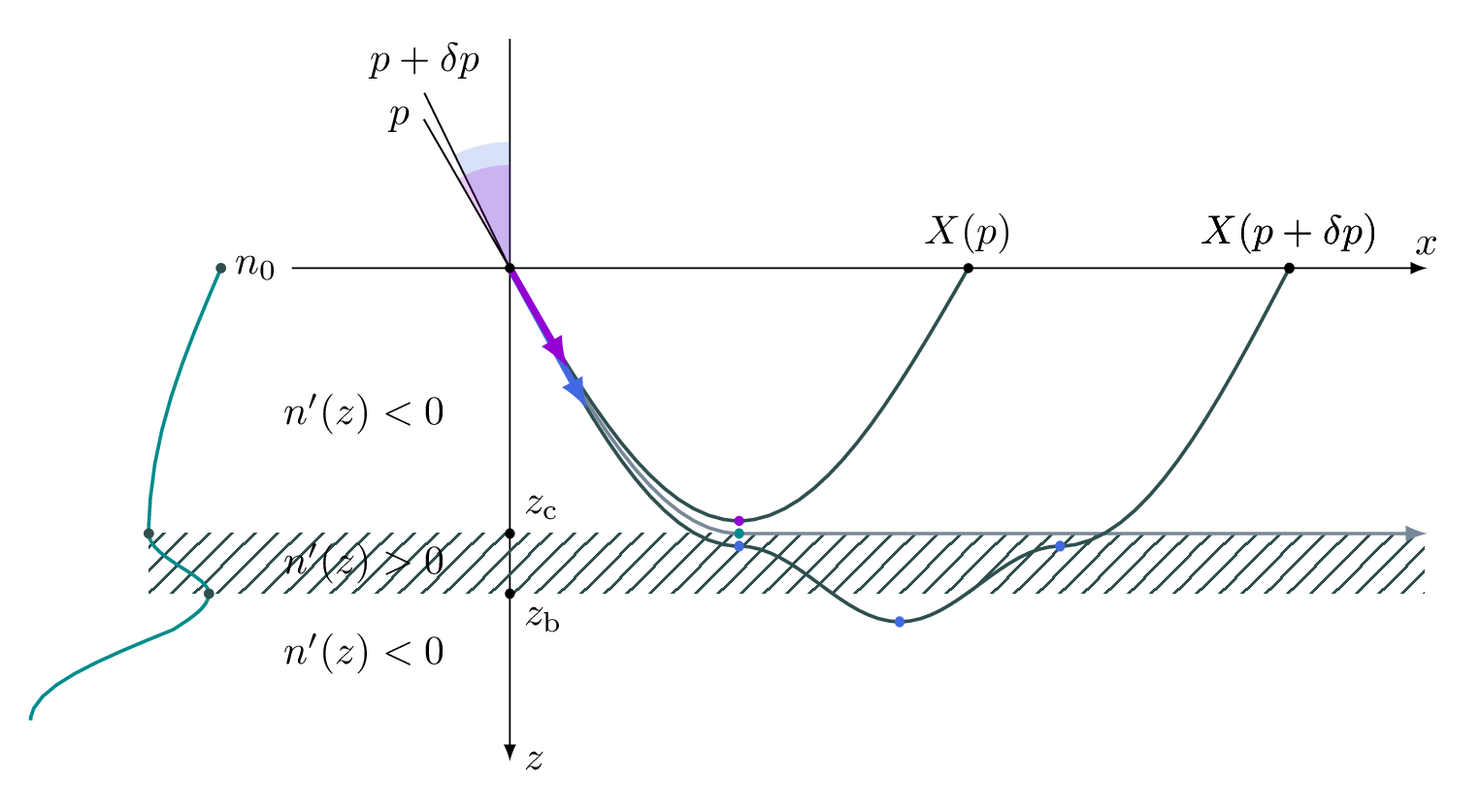
Kršenje nadomestne predpostavke bo gotovo povzročilo nezveznost napovedne funkcije \(X(p)\). To lahko preprosto vidimo na nazornemu primeru nizko-hitrostne cone (ang. low-velocity zone). Kot na sliki 3 si predstavljamo profil kot zvezno funkcijo, kjer imamo na nekem intervalu \((z_\mathrm{c}, z_\mathrm{b})\) naraščajoč lomni količnik, za \(z < z_c\) pa je funkcija padajoča.
V točki tik nad kritično \(z = z_c - \varepsilon\), bo žarek s parametrom \(p\) s dosegel dno, nato pa se glede na dno levo-desno simetrično navzgor vrnil na površino, na dometu \(X(p)\). Žarek s poljubno malo večjim parametrom \(p + \delta p\) bo ubral kvalitativno drugačno pot, kjer se bo ukrivil navzdol, nato pa šele po izstopu iz nizko-hitrostne cone dosegel dno in se simetrično vrnil na površino. Očitno je, da tedaj taka nizko-hitrostna cona povzroči nezveznost v napovedni funkciji (za ilustracijo primera glej sliko 9).
V analogiji z Abelovim mehanskim problemom še bolj intuitivno jasno, da takšna nizko-hitrostna cona onemogoča rekonstrukcijo profila. V Abelovem problemu namesto profila \(n(z)\) gledamo obliko klančine \(z(x)\) (slika 2), ki mora biti padajoča injektivna funkcija. Kršenje padajoče injektivnosti za zvezno klančino pomeni, da ima klančina prisoten vsaj en lokalni minimum, vdolbinico v klančini. Če kroglo pri kotaljenju na začetku postavimo na tako mesto, da se lahko krogla odkotali v lokalni minimum, bo v taki vdolbinici jasno obtičala – čas kotaljenja bo neskončen in iz njega ne bomo mogli na noben način rekonstruirati oblike tega dela klančine.
Kot bo bolj jasno v razdelku 5.4, je v primeru, inverz lahko poiščemo, le ta podan kot parametrični integral po \(p \mapsto (X, p)\), ki se začne pri \(p = n_0\), konča pa pri \(p = n\), za katerega določamo impliciten profil \(z(n)\). Profil \(z(n)\) lahko rekonstruiramo le od površinskega \(n_0\) do vrednosti \(p = n(z_\mathrm{max})\), do katere neprekinjeno poznamo napovedno funkcijo \(X(p), p \in [n(z_\mathrm{max}), n_0]\).
Če torej napovedna funkcija \(X(p)\) vsebuje nezvezni skok pri \(p=n_c\), lahko rekonstruiramo zgolj profil pred tem skokom, \(z(n)\) za \(n \in [n_c, n_0]\). Na intuitiven, a ne nujno pravilen način je to intuitivno mogoče razumeti s tem, da žarki tipajo profil \(z(n)\) le do največje dosežene globine \(z_\mathrm{max}\).
Degeneracija zaradi odseka s konstantno hitrostjo zvoka
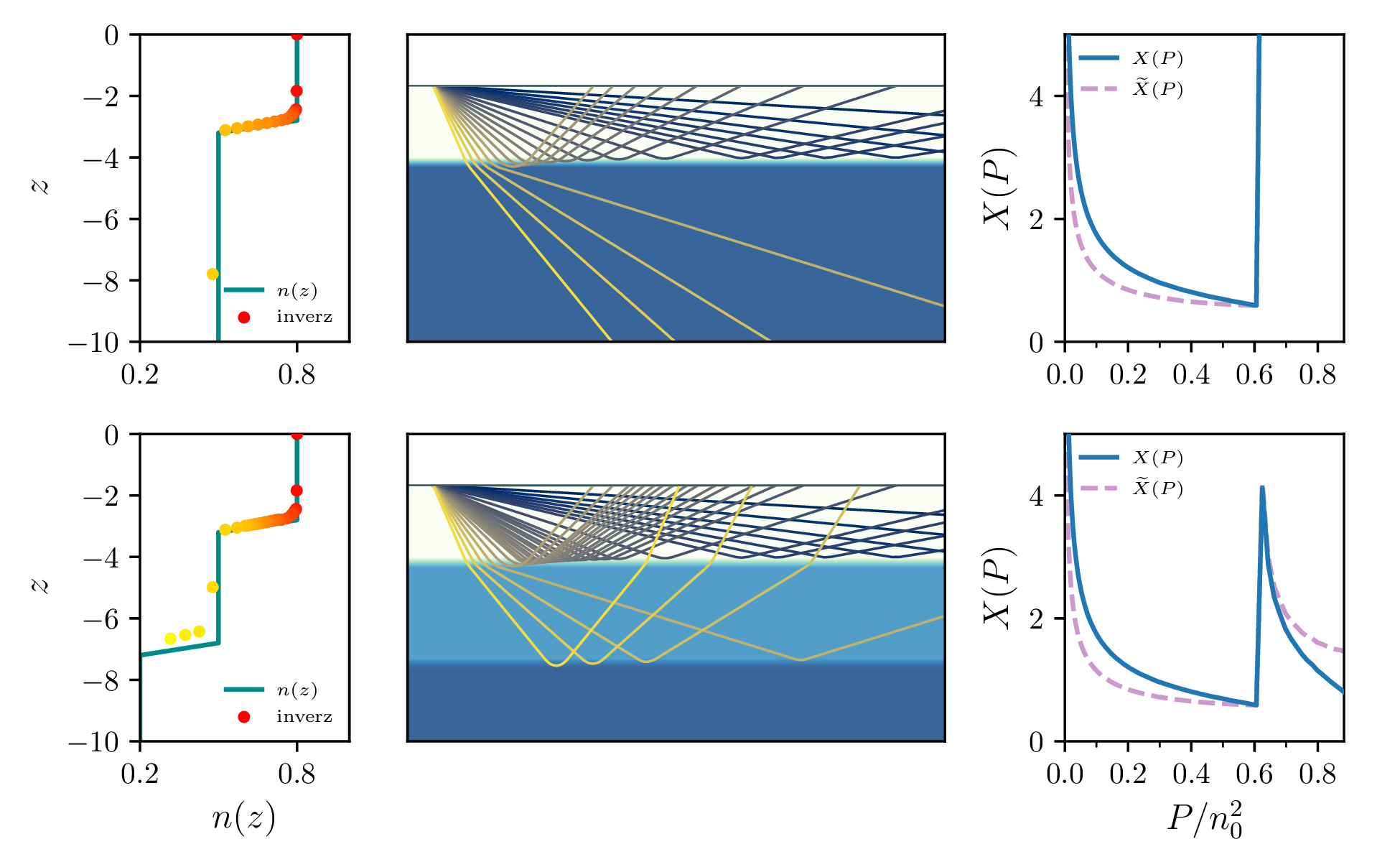
Poseben primer degeneracije dometa \(X = \infty\) dobimo v primeru, ko je v profilu prisoten odsek z konstantno hitrostjo zvoka. V takem odseku žarki potujejo v ravnih črtah, kar povzroči prepoznavno obliko nezveznosti v \(X(P)\).

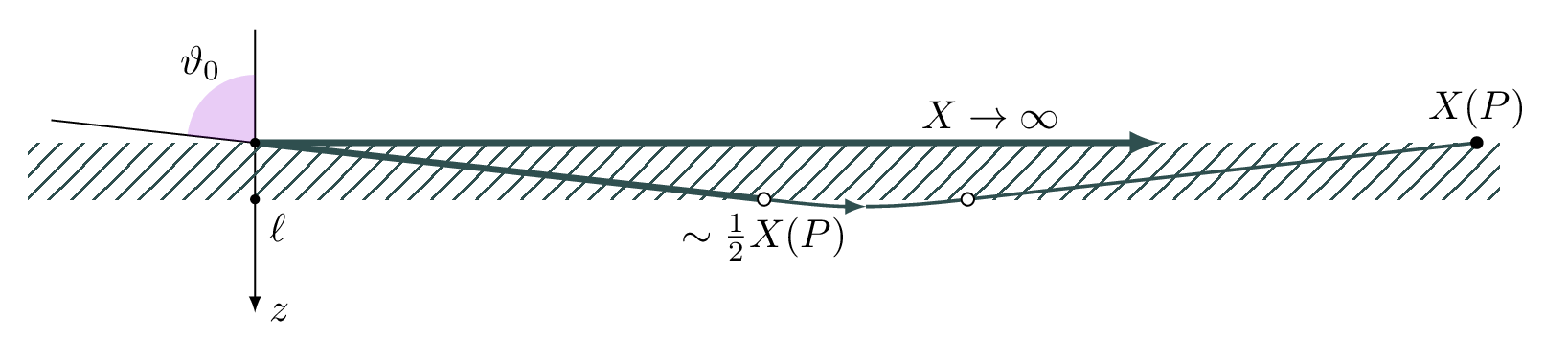
V analogiji z Abelovim problemom si predstavljamo odsek klančine, raven in z dolžino \(\ell\) (glej sliko 4 zgoraj). Če kroglo začetno postavimo na tak raven odsek, torej pri višini \(h\), se ne bo premaknila iz začetnega mesta in \(T(h) = \infty\). Prestavljajmo si, da kroglo premaknimo tik pred začetek ravnega odseka (krogla \(A\) na sliki |reffig:flat-rolling), na višino \(h + \delta h\). Po ohranitvi energije bo na ravni odsek prispela s hitrostjo \(v \propto \sqrt{\delta h}\). Če je \(\delta h\) majhen, lahko v času potovanja zanemarimo čas od \(h + \delta h\) do začetka odseka \(\ell\), upoštevamo pa le čas potovanja po odseku
\[T(h+\delta h) \approx T(h) + \frac{\ell}{\sqrt{\delta h}}.\]
V primeru odseka s konstantno hitrostjo zvoka (slika 4 spodaj) je podobno. Recimo da je odsek konstantne hitrosti na gladini. Za nek vstopni kot \(\vartheta_0\), ki se bliža pravemu kotu, bo žarek prepotoval pot \(\frac{\ell}{\sin\vartheta_0} = \frac{\ell}{\sqrt{\delta P}}\). Po izstopu iz odseka se bo žarek ukrivil navzgor in simetrično potoval navzgor. Dolžina, v kateri se žarek ukrivi, postane v limiti majhnega \(\delta P\) zanemarljiva v primerjavi s prepotovano \(x\)-razdaljo v odseku konstantne hitrosti.
Če je odsek konstantne hitrosti prisoten nekje pod gladino, bomo tako obnašanje za žarke \(\mathcal{P}\), ki imajo dno tip nad začetkom cone konstantne hitrosti
\[X(P+\delta P) \approx X(P) + \frac{\ell}{\sqrt{\delta P}}.\]
Ilustracijo takega pola vidimo na sliki 5. Na sliki 10 vidimo tak pol na primeru konkretnega profila, med trajektorijami vidimo tiste, za katere je \(\mathcal(P + \delta P) \to \infty\), ko gre \(\delta P \to 0\).
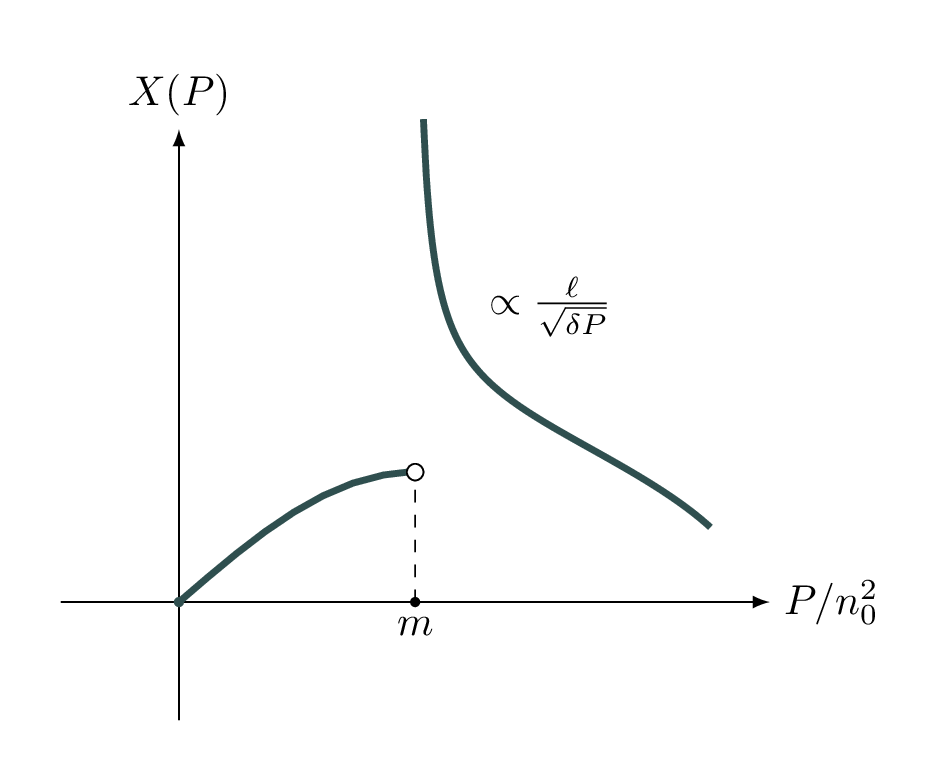
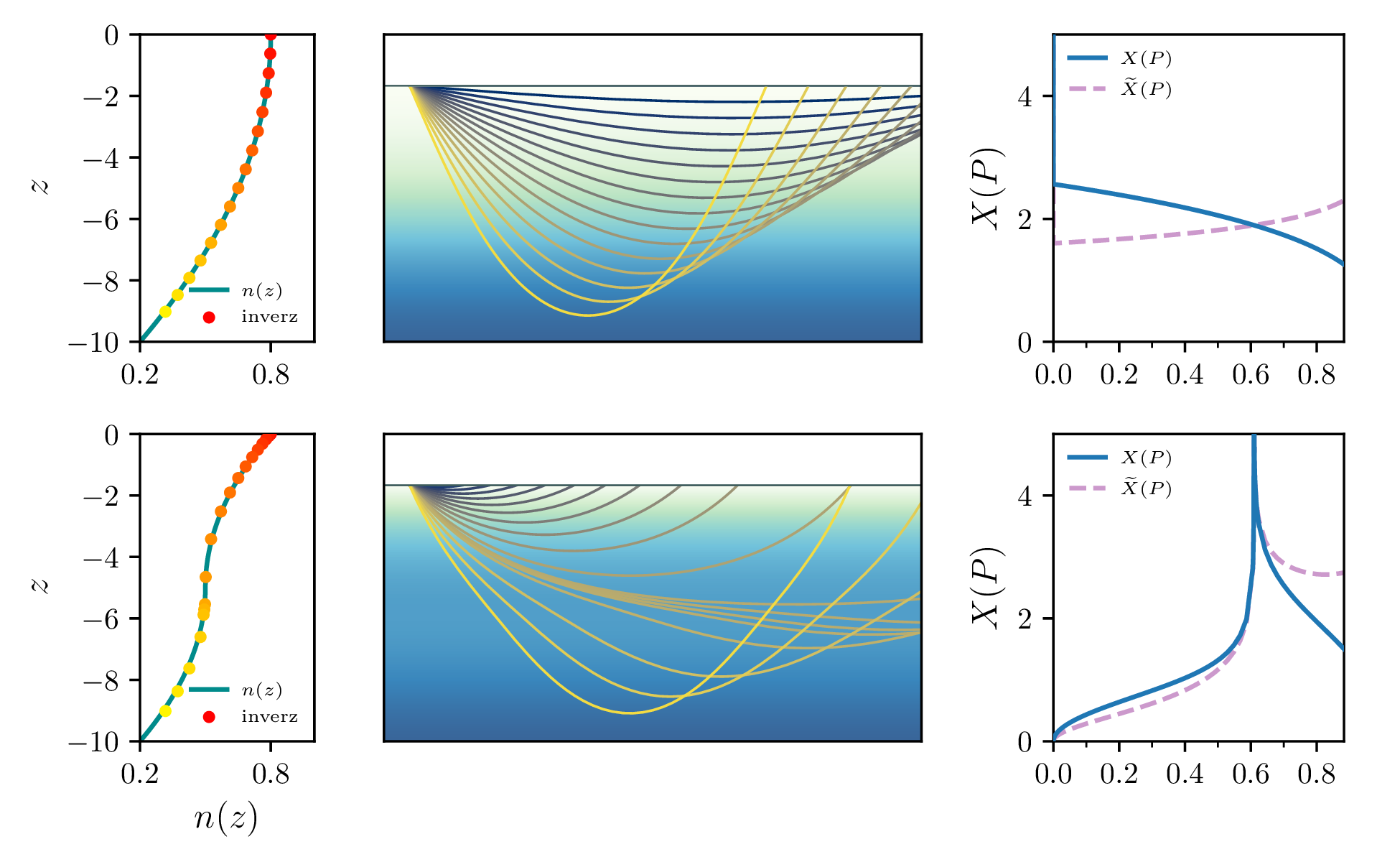
Degeneracija zaradi ničelnega odvoda
Za degeneracijo \(X = \infty\) je dovolj že to, da je profila lokalno konstanten, \(n'(z) = 0\). Ilustracijo takega žarka vidimo na sliki 3, kjer je tik na robu nizko-hitrostne cone zvezno odvedljivega profila tudi \(n'(z) = 0\).
Povsem neformalno, take singularnosti so drugačne od singularnosti \(\frac{1}{\sqrt{\delta P}}\), saj so lahko (ne pa nujno) odstranljive. S tem mislimo, da je \(X(P) = \infty\) zgolj za en \(P\), v poljubno tesni okolici pa se napovedna \(X(P)\) obnaša nedegenerirano.
Na primeru konkretnega profila na sliki 11 je odvod ničelen na gladini, \(n'(0) = 0\). Prisotna je degeneracija za \(P = 0\), kjer žarek spustimo v smeri vzporedno z ravnino, kjer žarek neovirano drsi ob gladini in je \(X(P = 0) = \infty\). A to velja le za \(P = 0\), če je \(P > 0\), četudi majhen, je \(X(P) < \infty\). Kot bomo videli v razdelku 5.5 lahko tak profil, kjer je \(\lim_{P \to 0^+} X(P) = X_0\), še vedno rekonstruiramo.
Različne oblike inverzijske formule
Če nazaj uvedemo staro spremenljivko \(p = \sqrt{n_0^2 - P}\) in upoštevamo, da je \(u = n_0^2 - n(z)^2\), lahko zapišemo iverz v od-prej-znanih količinah
\[\begin{aligned} \frac{1}{\pi} \int_0^u \frac{X(P) / 2p}{\sqrt{u - P}} \,\mathrm{d}P = -\frac{1}{\pi} \int_{n_0}^{n(z)} \frac{X(p)}{\sqrt{p^2 - n^2}} \,\mathrm{d}p. \end{aligned}\]
Ta rezultat je tedaj t. i. Herglotz-Weichertova inverzijska formula [7], [8]
\[z(n) = -\frac{1}{\pi} \int_{n_0}^{n} \frac{X(p)}{\sqrt{p^2 - n^2}} \,\mathrm{d}p.\]
Ker je \(p > 0\), velja \(\mathrm{d}\big(\mathop{\mathrm{arcosh}}\frac{p}{n} \big) = \frac{\mathrm{d}p}{\sqrt{p^2 - n^2}}\) in inverzijsko formulo lahko zapišemo še na en način
\[\begin{aligned} z(n) &= -\frac{1}{\pi} \int_{n_0}^n X(p) \left[ \frac{\mathrm{d}\left(\mathop{\mathrm{arcosh}}\frac{p}{n} \right)}{\mathrm{d}p} \right]_p \,\mathrm{d}p \\ &= \frac{1}{\pi} \int_{n_0}^n \mathop{\mathrm{arcosh}}\left(\frac{p}{n}\right) \left[ \frac{\mathrm{d}X}{\mathrm{d}p} \right]_p \,\mathrm{d}p \\ &= \frac{1}{\pi} \int_{[X]_{p=n_0}}^{[X]_{p=n}} \mathop{\mathrm{arcosh}}\left( \frac{p}{n} \right) \,[\mathrm{d}X]_p, \end{aligned}\]
kjer smo integrirali po delih in uvedli integracijo po novi spremenljivki. Bralca bi lahko zmotilo dejstvo, da smo za novo spremenljivko uvedli \(X(p)\), za katero vemo, da ni nujno injektivna. Pravzaprav smo \([\mathrm{d}X]_p\) uvedli v smislu integracije po parametrični krivulji \(p \mapsto (X, p)\), kar je še vedno zelo priročna oblika za numerično vrednotenje inverzijske formule, kot bomo to videli v razdelku 7.2. Za spodnjo mejo v tem integralu bomo predpostavili, da je \(n'(z) \neq 0\), kar pomeni, da je \([X]_{p = n_0} = 0\), zato lahko rešitev Herglotz-Weichertove inverzije zapišemo na drugačen način kot
\begin{equation}z(n) = \frac{1}{\pi} \int_{0}^{[X]_{p=n}} \mathop{\mathrm{arcosh}}\left( \frac{p}{n} \right) \,[\mathrm{d}X]_p. \label{eq:cosh}\end{equation}
Zapisani integral (17) razumemo kot predpis, ki podaja \(z(n)\) za določeno vrednost lomnega količnika \(n \in (0, n_0]\), če le poznamo pa \(X(p)\), kjer \(p \in (0, n_0]\) (predpis 2). Ta parametrični integral je ilustriran na sliki 6.
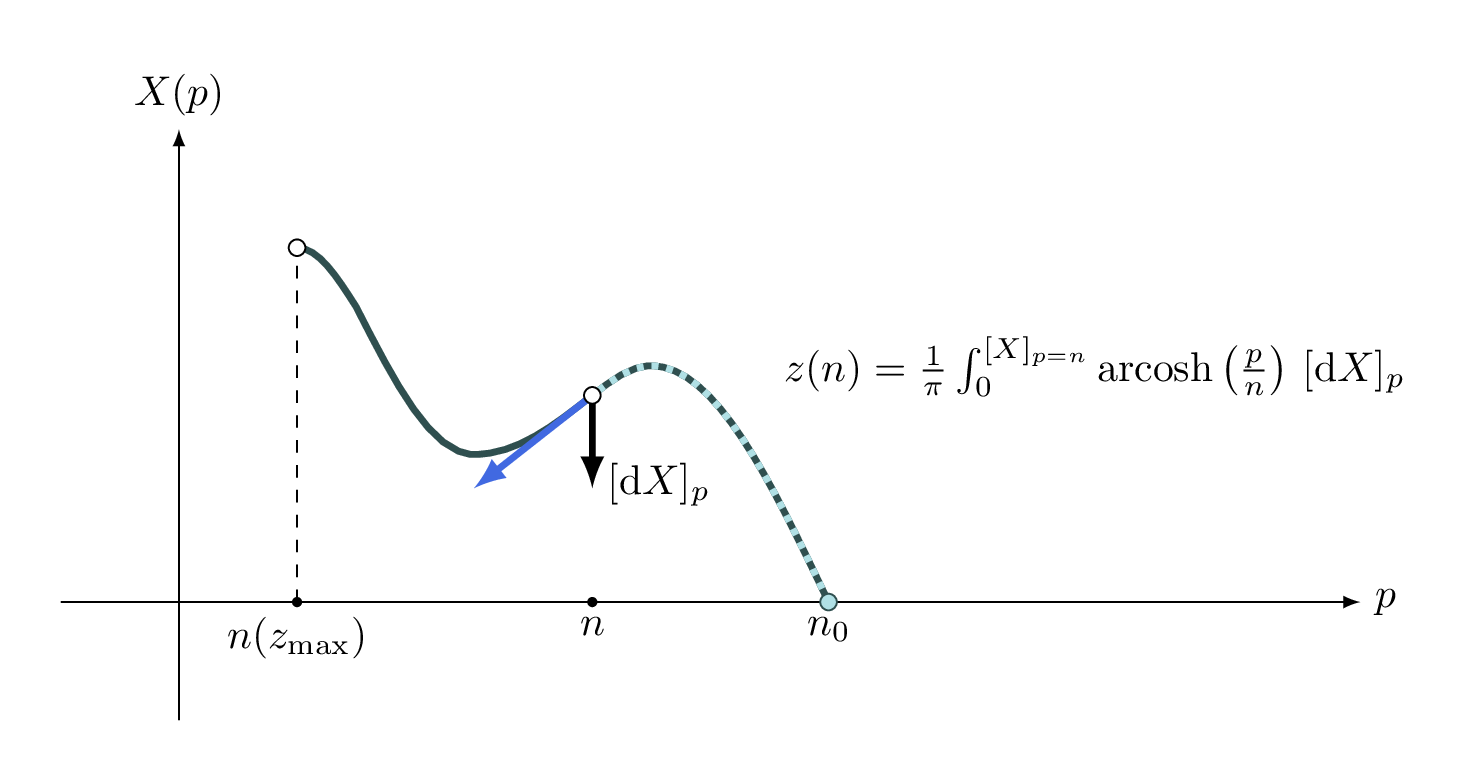
Degeneracije kot limitni primer nedegeneriranih krivulj
Pojasnili smo že, do kakšne degeneracije vodi profil \(n_\mathrm{deg}(z)\), ki ima na gladini ničelen odvod \(n_\mathrm{deg}'(0) = 0\). Če v naravi izmerimo nek realen profil, pa je zelo malo verjetno, da ga bo opisovala matematično idealizirana funkcija z ničelnim odvodom na gladini.
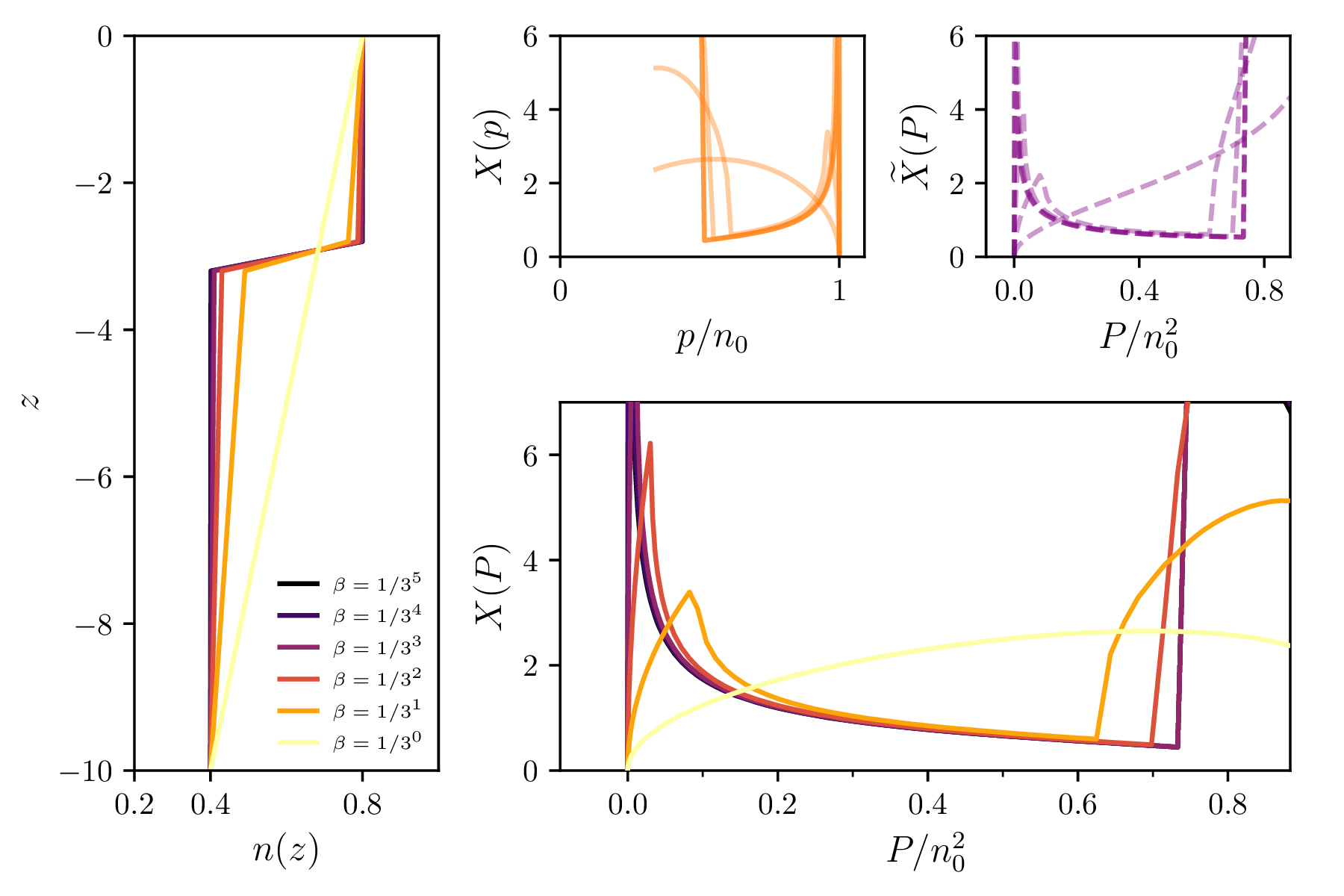
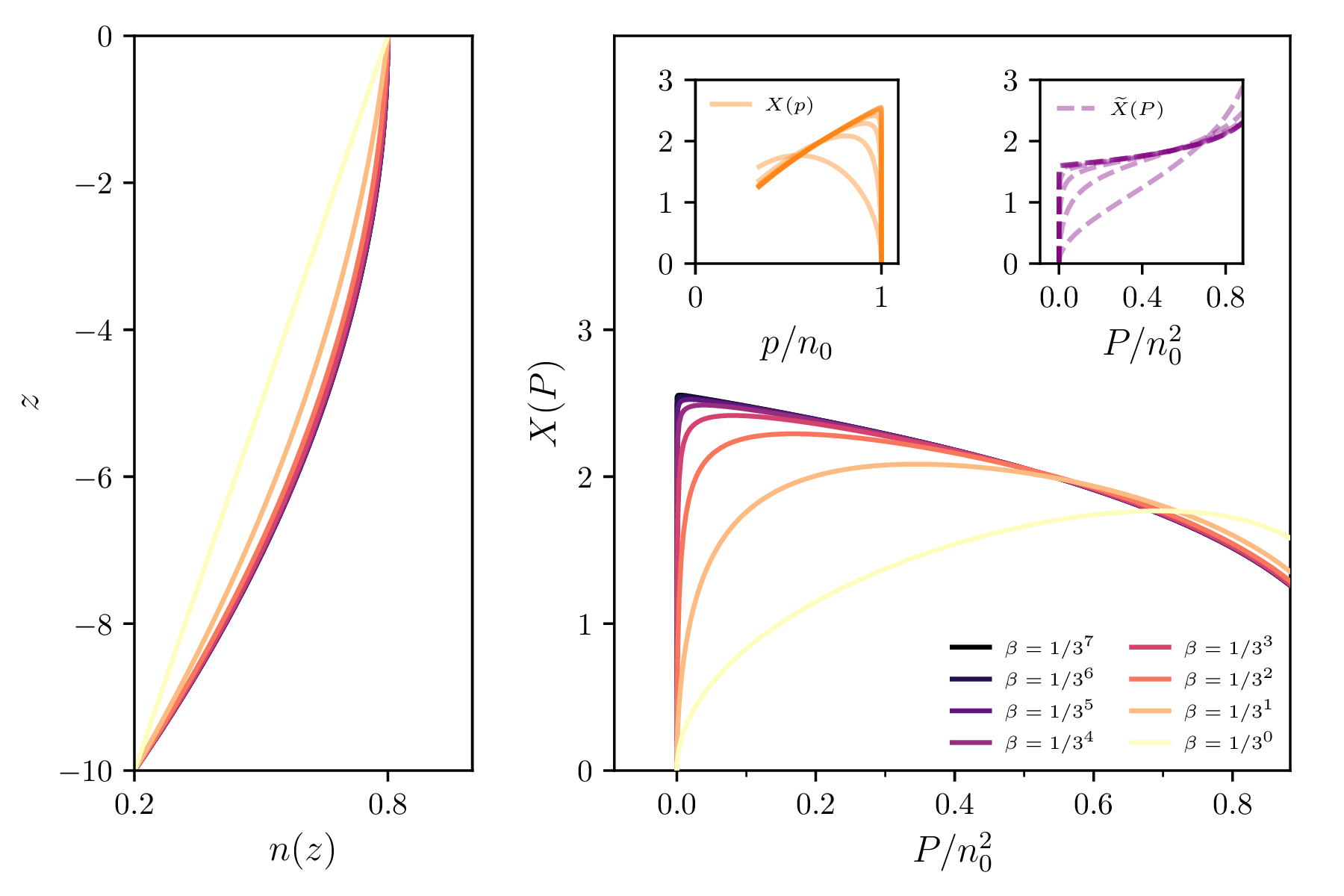
Namesto degeneriranega primera samega si zatorej zamislimo zaporedje profilov, ki imajo na gladini neničelen odvod, hkrati pa konvergirajo k idealiziranem profilu \(n_\mathrm{deg}(z)\), ki privede do omenjene degeneracije. Primer takega zaporedja je npr. parametrično podana družina
\begin{equation}n_\beta(z) := n_0 - (n_1 - n_0) \left\{ (1-\beta)z^2 + \beta z \right\}, \quad z \in [0, 1]. \label{eq:n-beta}\end{equation}
Za \(\beta = 0\) je tak profil degeneriran in povzroči \(X_{\beta = 0}(P = 0) = \infty\). A za vse druge \(\beta \in (0, 1]\) je profil nedegeneriran in za vse velja, da je \(X_{\beta > 0}(P = 0) = 0\). Za parametriziran profil \(n_\beta\) lahko tako obnašanje opazimo na sliki 7.
To motivira, da formulo (17) razširimo na primere, kjer je
\[X_0 := \lim_{P \to 0^+} X(P) \neq 0.\]
Če zanemarimo malo verjetne degenerirane profile, se zaporedje nedegeneriranih približuje funkciji, ki v majhni okolici \(P \in (0, \varepsilon)\) naraste na neko vrednost \(X_0\), v točki \(0\) pa še vedno velja \(X(P = 0) = 0\). Tako se odvod \(\frac{\mathrm{d}X}{\mathrm{d}P}\) v tej okolici \((0, \varepsilon)\) približuje Dirac delta funkciji \(X_0 \delta(P)\).
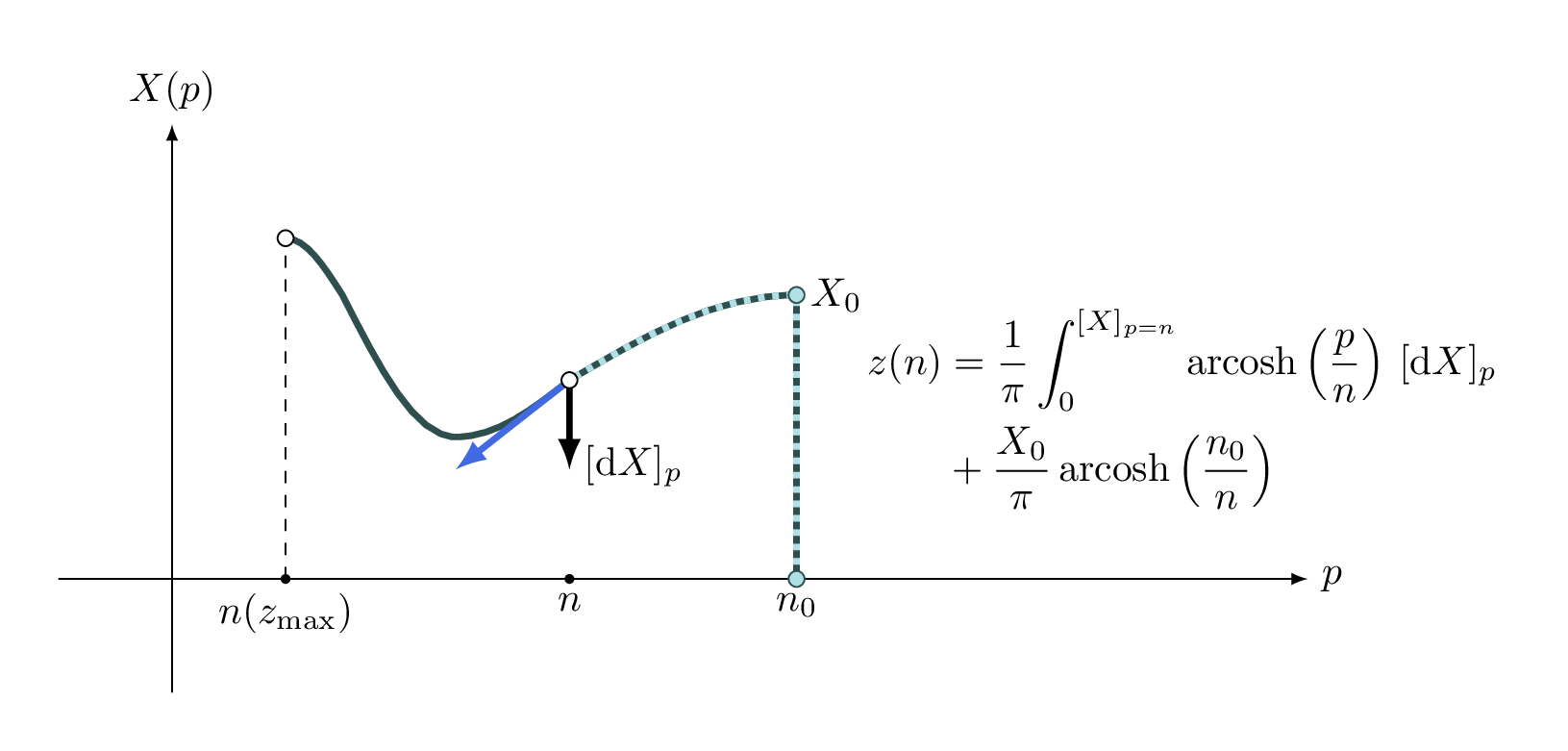
Povedano v spremenljivki \(p\), se v okolici \(p in (n_0 - \varepsilon, n_0)\) odvod \(\frac{\mathrm{d}X}{\mathrm{d}p}\) približuje \(X_0 \delta(p)\). Namesto izraza (17) tedaj dobimo parametrično integracijo (glej tudi sliko 8)
\begin{equation}z(n) = \frac{1}{\pi} \int_{[X_0]_p=n_0}^{[X]_{p=n}} \mathop{\mathrm{arcosh}}\left( \frac{p}{n} \right) \,[\mathrm{d}X]_p + \frac{X_0}{\pi} \mathop{\mathrm{arcosh}}\left( \frac{n_0}{n} \right). \label{eq:cosh-extended}\end{equation}
Vredno je omeniti še manjši trik, ko integral (19) vrednotimo numerično. Namesto prištevanja drugega člena je dovolj le to, da eno začetno točko \(X(p = n_0)\) ali \(X(P = 0)\) umetno nastavimo na vrednost 0.
Povzetek najpomembnejših rezultatov
Injektivnost Profil6 \(n(z)\) je padajoča injektivna funkcija. Če je \(n(z)\) padajoča injektivna funkcija le na nekem intervalu \([0, z_c]\), lahko rekonstruiramo profil v obliki \(z(n)\) le za \(n \in [n_0, n(z_c)]\).
Zadostni pogoj za Herglotz-Weichertove inverzijsko formulo Za veljavnost inverzijske formule (19) je zadostno, da je \(\widetilde{X}(P)\) omejen v neki okolici \(P \in (0, \delta]\), drugje pa je \(\widetilde{X}(P)\) omejen ali pa ima končno število polov stopnje \(\gamma < \frac{1}{2}\). Tedaj profil rekonstruiramo preko formule
\[z(n) = \frac{1}{\pi} \int_{[X_0]_p=n_0}^{[X]_{p=n}} \mathop{\mathrm{arcosh}}\left( \frac{p}{n} \right) \,[\mathrm{d}X]_p + \frac{X_0}{\pi} \mathop{\mathrm{arcosh}}\left( \frac{n_0}{n} \right).\]
Nekaj numeričnih eksperimentov
Numerični račun inverzije
Zgolj za mero kompletnosti lahko podamo še primer, kako preprosta je lahko implementacija numerične Herglotz-Weichertove inverzije
X_vals [0] = 0 # This allows us to handle some degenerate casesn_vals = p_valsp_over_n = np.outer (1 / n_vals , p_vals) # p_j / n_i""" Integrate arcosh (p_j/n_i) over X_j , from 0 to X_i = X(p = n_i)"""upper_bound_mask_idx = np.triu_indices(len(p_vals), k=-1)p_over_n[ upper_bound_mask_idx ] = 1.0 # That way arccosh (1) = 0, maskedreconstructed_z_vals = 1 / np.pi * np.trapz(np.arccosh(p_over_n), X_vals , axis =1)
Napovedi dometa in primeri
Za določen profil \(n(z)\), lahko napovedni problem za funkcijo \(X(p)\) rešimo tako, da preprosto integriramo enačbo (1) in preverimo, kdaj žarek ponovno predre gladino. Vektorsko enačbo (1) enostavno prevedemo na sistem navadnih diferencialnih enačb
\[\frac{\mathrm{d}}{\mathrm{d}t} \begin{pmatrix} v_x \\ v_z \\ x \\ z\end{pmatrix} = \begin{pmatrix} -\frac{n'}{n} v_z v_x \\ -\frac{n'}{n} (v_z^2 - 1) \\ v_x \\ v_z \end{pmatrix}, \quad \mathbf Z_0 = \begin{pmatrix} \sin \vartheta_0 \\ -\cos \vartheta_0 \\ 0 \\ 0 \end{pmatrix},\]
pri čemer začetni pogoj \(\mathrm Z_0\) določa začetek v izhodišču, z žarkom usmerjenim pod \(\vartheta_0\) (slika 1).
Napovedno funkcijo \(X(\vartheta_0)\), sicer v parametrizaciji po \(P = n_0^2\cos^2\vartheta_0\), je tedaj preprosto izračunati. Za neko vrednost \(P\) določimo začetni pogoj, nato pa sistem vektorskih enačb integriramo do točke, kjer žarek zopet seka gladino \(x = X(P)\).
Na ta način smo poračunali napovedne funkcije dometa za profile v slikah 9, 10, 11, 12 in 7.