Gauss-Laguerrovi snopi
WebGl programček za vizualizacijo Gauss-Laguerrovih snopov z emisijsko-absorbcijskim modelom
Gauss-Laguerrovi snopi so rešitve obosnega približka valovne enačbe [1], [2]. Identificiramo jih z celoštevilskima redoma \((p, \ell)\), kjer je \(p > 0\). \begin{equation}\psi_{p\ell} (r, \varphi, z) = \frac{w_0}{w} \left( \frac{\sqrt{2} r}{w} \right)^{|\ell|} L_p^{|\ell|} \left( \frac{2r^2}{w^2} \right) e^{i\ell \varphi} e^{ikr^2 / 2q} e^{-i\eta_{p\ell}(z)}, \label{eq:beam}\end{equation} pri čemer je kompleksni krivinski radij \(q\) definiran kot \[\frac{1}{q} = \frac{1}{R} + i\frac{2}{kw^2} = \frac{z}{z^2 + z_0^2} + \left( \frac{i}{k w_0^2} \right) \frac{1}{1 + \frac{z^2}{z_0^2}},\] kar vključuje tako krivinski radij paraboličnih valovnih front \(R\) in širino snopa \(w\). Obe količini se spreminjata vzdolž žarka, sicer kot \begin{equation}R(z) :=z \left( 1 + \frac{z_0^2}{z^2} \right), \quad w^2(z) :=w_0^2 \left( 1 + \frac{z^2}{z_0^2} \right). \label{eq:R-and-w}\end{equation} Dodatno ima faza snopa še eno bolj homogeno komponento \(\eta_{p\ell}\), ki se ne spreminja z cilindričnim radijem \(r\), temveč je z potjo vzdolž osi. \[\eta_{p\ell}(z) = (2p + |\ell| + 1) \arctan \left( \frac{z}{z_0} \right).\] Posebej zanimiv pa je v (1) faktor \(e^{i\ell\varphi}\). Ta predstavlja \(\ell\)-krat ponovljen potek faze od \([0, 2\pi)\), v ali v obratni urinega kazalci glede na predznak \(\ell\). Ta faza je tudi ključni element, ki da snopu tirno vrtilno količino [3].
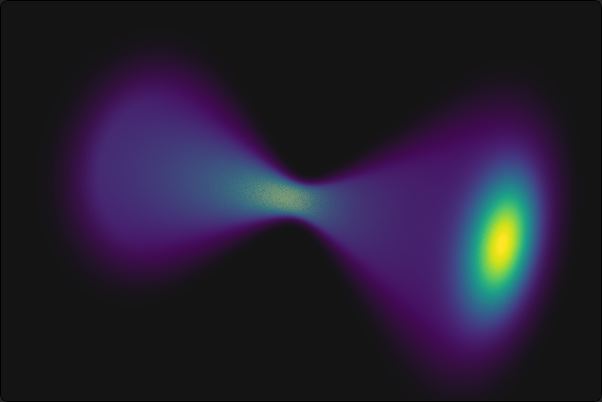
Vizualizacija snopa
Osnovna ideja za vizualizacijo je to, da upodobimo skalarno polje \(v(\mathbf r) \in \mathbb{R}\) v 3 dimenzijah. V namen tega upodobimo presevno sliko (ang. volumetric render), ki posnema procesa emisije in preprosto eksponentno atenuacijo [4]. Tako posamezni volumni oddajajo \(\propto v(\mathbf{r})\) svetlobe, izsevana svetloba pa se pri poti skozi snov proti kameri absorbira. Če pot začne na razdalji \(s\) od kamere, se pri celotni poti do kamere izsevana svetloba atenuira za faktor \[e^{-\int_0^s v(t) \,\mathrm{d}t}\] Polje opazujemo s točkovno kamero, katere piksli pokrijejo nek nabor prostorskih kotov \(\Omega\). Na tej poti je torej \(v(t) = v(\mathbf{r}(t))\), pri čemer je žarek \(\mathbf{r}(t)\) določen s prostorskim kotom. Za žarek iz točkovne kamere pod nekim kotom je opažena intenziteta vsota izsevanih in atenuiranim prispevkom vseh volumnov, ki jih žarek seka \[I(\Omega) = \int_0^\infty v(s)\, e^{-\int_0^s v \,\mathrm{d}t} \,\mathrm{d}s.\] Numeričen približek takega integrala nam tedaj da sliko \(I(\Omega)\), ki predstavlja naše realno skalarno polje v 3 dimenzijah. Po zgledu [4] sem implementiral preprost WebGL programček, s katero lahko na ta način vizualiziramo realna skalarna polja.
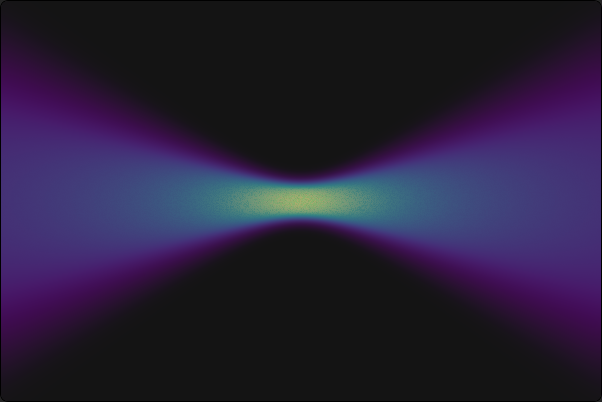
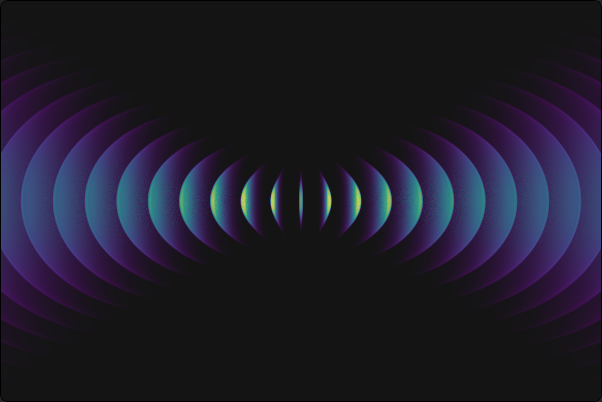
Gauss-Laguerrovov snop, ki ga želimo vizualizirati, pa je podan z kompleksnim skalarnim poljem. En način za vizualizacijo je prikaz same intenzitete polja1 \[\text{amplitudna slika: } v(\mathbf{r}) :=\| \psi_{p\ell} (r, \varphi, z) \|.\]
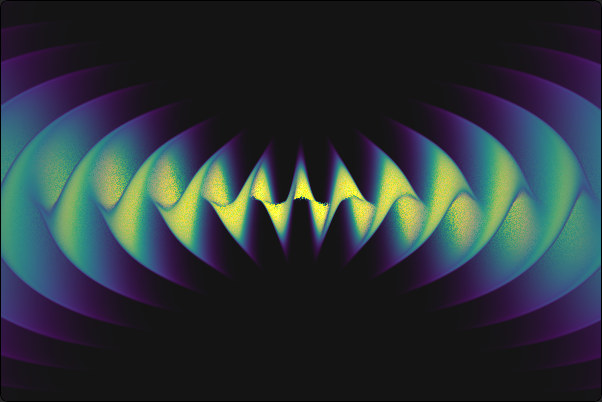
Na sliki 1 vidimo v perspektivi prikazano amplitudno sliko Gaussovega snopa. Drugi način, ki pa bolj jasno razkrije fazno strukturo snopa, pa je prikaz valovnih front. Ideja je, da prikažemo intenziteto, a prikaz omejimo le na eno valovno fronto, torej na neko površino konstantne faze \(\vartheta_0\) \[\text{valovne fronte: } v(\mathbf{r}) :=\delta(\vartheta - \vartheta_0) \cdot \| \psi_{p\ell} (r, \varphi, z) \|, \quad \psi_{p\ell} = \| \psi_{p\ell} \| e^{i\vartheta},\] pri tem je \(\delta(x)\) neka ozka, Dirac-delta funkciji podobna funkcija z vrednostjo \(1\) pri \(x=0\) in vrednostjo \(0\) pri \(|x| \gg 0\). Za ilustracijo je sliki 2 razvidna primerjava med amplitudno sliko in sliko valovnih front za Gaussove snop. Dodam naj, da zahtevamo od te \(\delta(x)\) funkcije periodičnost na \(2\pi\), saj je faza tam periodična. Konkretno za našo rabo izberemo \[\begin{aligned} \delta(\vartheta - \vartheta_0) :=1 - \mathop{\mathrm{smoothstep}}\left(0, \sigma, \mathop{\mathrm{fract}} \left( \frac{\vartheta - \vartheta_0}{2\pi} \right)\right)& \\ + \mathop{\mathrm{smoothstep}}\left(1-\sigma, 1, \mathop{\mathrm{fract}} \left( \frac{\vartheta - \vartheta_0}{2\pi} \right)\right),& \end{aligned}\] pri čemer sta fract in smoothstep dve klasični GLSL funkciji.
Zanimivi snopi
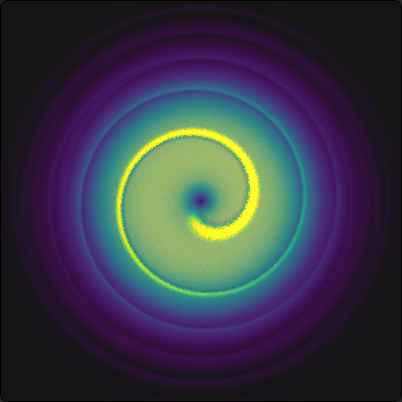
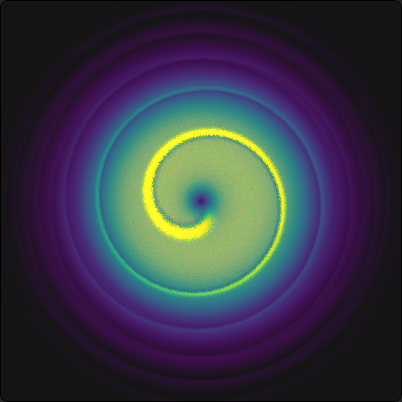
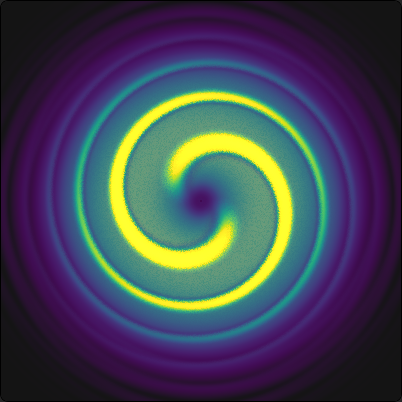
Poleg relativno nezanimivega Gaussovega snopa \(\psi_{00}\), si lahko pogledamo drugi najpreprostejši Gauss-Laguerrovov snop \(\psi_{01}\). V amplitudni sliki je pravzaprav podoben Gaussu, le z ničlo pri \(z\)-osi, saj nam to narekuje faktor \(\left( \frac{\sqrt{2} r}{w} \right)\) v snopu (1). Povsem drugače pa izgleda oblika valovnih front. Kot vidimo na sliki 3, so valovne fronte v obliki vijačnice, z maksimumom pri nekem končnem \(r\). Koliko števna je ta vijačnica, je odvisno od \(|\ell|\), smer pa od predznaka \(\ell\). To lepo vidimo tudi v prerezih na sliki 4.